基于精确线性化理论的超级电容储能系统的非线性控制算法

李 轩 李永丽 常晓勇

(智能电网教育部重点实验室(天津大学) 天津 300072)



基于精确线性化理论的超级电容储能系统的非线性控制算法

李 轩 李永丽 常晓勇

(智能电网教育部重点实验室(天津大学) 天津 300072)

针对超级电容及DC-DC电路的非线性特性，设计了超级电容储能系统的非线性控制算法。通过分析电路的工作状态，建立了电路仿射非线性系统标准型，利用状态反馈精确线性化理论推导出电路状态量与占空比函数间的关系，进而设计相应控制算法，并证明了系统的内动态稳定性，实现了超级电容恒流充电与恒压放电的控制目标。在Matlab/Simulink仿真平台中搭建仿真模型，对所提控制算法进行验证，并在实验室中搭建实验电路，比较了非线性控制算法与PI算法的控制效果。结果表明，在超级电容储能系统中采用非线性控制算法相比于传统PI算法能明显提高系统的动态性能，保证系统稳定运行。

超级电容 储能系统 非线性控制 状态变量反馈 精确线性化

0 引言

随着国际能源危机的加剧以及环境保护的迫切需求，分布式发电技术已经成为当前的研究热点[1]。由于风能、太阳能等新能源自身具有间歇性和波动性的特点，导致分布式新能源并网控制困难，不能直接接入配电网，为此，提出了微电网的概念[2]。微电网是一种由分布式电源、储能系统(Energy Storage System，ESS)、负荷以及电力电子装置等组成的自治系统[3]。其中，储能装置的作用是在发电设备的输出功率大于负载需求时吸收多余能量，而当输出功率不足时释放能量为负载供电。因此，储能装置的引入可以较好地改善微电网内由于发电机出力或负荷需求随机变化所导致的功率不平衡现象，提高微电网的稳定性[4]。

目前常见的储能方式主要有蓄电池储能、超导储能、飞轮储能、超级电容储能等。超级电容作为一种功率型储能元件，具有体积小、维护简单、对环境无污染、寿命长的特点，且响应速度快、功率密度大，因此对分布式电源输出功率的波动具有较好的抑制效果[5]。

储能元件一般通过电力电子电路与母线或负载相连，并采用PI控制算法进行控制[6]。然而电力电子电路本身是一种典型的时变非线性电路，并且如果负载不仅是电阻等线性负载，而是冲击性负荷或其他非线性负载，则更增强了电路的非线性特性。传统PI算法是基于误差的线性调节算法，将线性控制算法应用于非线性电路显然是不合适的，不仅动态响应慢，而且当电路参数变化时有可能产生分岔或混沌等非线性现象[7]，导致电压或电流的纹波系数较大。

近年来已经有很多学者将非线性控制算法应用到对电路的控制中，例如神经网络控制[8]、滑模控制[9]等。文献[10]采用精确反馈线性化的方法对Boost电路进行算法设计，但仅针对电源恒定的情况进行了实验验证；文献[11]针对飞轮储能系统设计了双环控制放电算法，但仅是数值仿真，没有经过实验验证；文献[12]采用恒定导通时间的方法对多输入系统进行控制，但理论推导过于复杂，并且公式计算较多，硬件实现较困难。

本文针对超级电容储能系统的非线性特性及控制目标设计相应的非线性控制算法。首先，基于电路工作状态方程，推导出系统仿射非线性系统标准型，应用输入-状态和输入-输出精确线性化理论研究系统状态量或输出量与控制输入量间的关系，设计相应控制算法，实现了超级电容恒流充电[13]与恒压放电的控制目标。在Matlab/Simulink中搭建仿真模型验证算法的有效性，然后通过搭建硬件电路对非线性控制算法与PI算法进行比较。实验结果表明，非线性控制算法相比于传统PI控制算法具有明显的优越性。

1 超级电容储能系统结构

本文研究的超级电容储能系统结构如图1所示，主要由超级电容器、双向DC-DC变换器以及直流电源和负载组成。其中，超级电容采用超级电容经典等效模型代替[14]。

图1 超级电容储能系统基本结构Fig.1 Structure of super capacitor energy storage system

充电时，开关K1导通、K2关断，直流电源E通过DC-DC电路给超级电容充电，超级电容存储能量；开关管VT2恒关断，VT1间断导通，电感电流流向从左向右，电路为Buck电路。

放电时，开关K1关断、K2导通，超级电容通过DC-DC电路向负载R放电，维持负载侧电压恒定；开关管VT1恒关断、VT2间断导通，电感电流流向从右向左，电路为Boost电路[15]。

充电时，超级电容相当于负载，而又与电阻性负载不同，它的端电压不断升高，但仍要保持充电电感电流大小不变；放电时超级电容相当于电源，但是随着超级电容放电深度不断加深，电容端电压也在不断下降，此时仍要维持负载侧电压恒定。因此，控制算法应能在超级电容电压大范围变化的情况下保持良好的适应性。同时，针对分布式能源输出功率的快速波动，超级电容的充放电功率也应能迅速调节。因此，控制算法也应具有快速动态响应特性。

本文将精确反馈线性化法应用于超级电容储能系统的控制设计中，可将对非线性系统的设计问题转为对线性系统的设计问题，继而易于设计相应的控制算法。此外，在线性化的过程中，该方法没有对任何高阶微分项进行忽略，因而能够保证控制系统的准确度。由于控制算法的设计建立在电路状态方程的基础上，因此本文首先对电路的充放电两种工作状态分别建立数学模型，进而设计相应的控制算法。

2 超级电容充电算法设计

2.1 充电Buck电路建模

当电路工作在给超级电容充电的状态时，开关管VT2恒关断、VT1采用恒频PWM调制。由于电路运行过程中开关频率远大于电路固有频率，因此可以采用状态空间平均法对电路建模[16]，得到电路的状态空间平均模型为

(1)

式中，E为直流电源电压值；iL和uSC分别为一个开关周期内电感电流和超级电容电压的平均值；CSC为超级电容的电容值；RS和RP分别为超级电容等效串联电阻值和等效并联电阻值；L为电感值；μ为占空比函数。

选取状态变量x1=iL、x2=uSC，可以得到以状态向量X=[x1，x2]表示的单输入仿射非线性系统的标准型

X′=f(X)+g(X)μ

(2)

式中

2.2 输入-状态精确线性化分析

根据文献[17]中给出的系统输入-状态精确反馈线性化的条件，对式(2)的系统进行验证。

1)由于本系统含有2个状态变量，所以系统维数n=2，需考察向量场{g，adfg}的线性相关性。

(3)

由式(3)可知，矩阵[g，adfg]的秩为2，因此集合{g，adfg}是线性无关的。

2)集合{g}是由单独的一个向量所组成的集合，显然满足非奇异对合分布条件。

因此，由Buck电路所建立的仿射非线性系统式(2)可以进行输入-状态精确线性化。

设新状态变量z1，z1是关于x1、x2的函数，根据输入-状态精确线性化的条件，z1需满足

z1·g=0

(4)

z1·adfg≠0

(5)

由式(4)可知，实际上z1是一个只含有变量x2(超级电容电压)，而不含变量x1(电感电流)的函数。而超级电容充电时需要对式(2)中的电感电流进行控制。因此，通过对该系统进行输入-状态精确线性化无法满足设计要求。

2.3 输入-输出精确线性化分析

对式(2)所示的单输入仿射非线性系统进行变换，增加一个包含电感电流量的输出函数，然后对新构造的输出函数进行输入-输出线性化以得到输出量与输入占空比之间的关系。取新的输出函数为电感电流量，得到单输入单输出仿射非线性系统的标准型

(6)

式中，y为系统输出函数。

输入-输出精确线性化的步骤就是不断对输出量进行微分，直到输入量出现在表达式中。经过严格的证明，对任意n阶能控系统的任一输出，最多只需微分n次就能使输出量和输入量出现在同一表达式中[18]。因此，对式(6)系统中的输出量进行微分

(7)

式(7)得到了输出量和输入量之间的显式关系。

令新控制变量

(8)

则原控制量可以用新控制量表示为

(9)

此时原系统式(6)转换为线性系统

y′=v

(10)

可见，原来对输入量μ的控制设计可以转为对新输入量v的设计。

系统的控制目标是使输出函数y跟踪参考电流值iLref。通常的设计方法是直接取y与iLref的差值作为误差量，通过控制算法的设计使误差量最终趋于0。然而这种设计方法会导致系统处于稳态时的波动较大，并且如果参数选择不当可能会产生稳态误差和次谐波现象[19]。因此，本文将误差的积分量引入设计过程，消除稳态误差的同时加快了系统的动态响应速度。

设新的变量

z=∫y-iLref

(11)

z′=y-iLref

(12)

(13)

选择新的控制输入量

v=-k1z′-k2z

(14)

式(14)中的参数k1、k2若选择适当，可以使式(10)所示系统为指数稳定的系统。并且当系统稳定时z和z′均趋于0，即满足输出量跟踪给定值的设计目标。

将式(14)代入式(9)，即可得到对原控制量μ的控制函数。

由于Buck电路正常工作时一共有2个状态变量，即电感电流iL和超级电容电压uSC，上述步骤只是对其中一个变量的跟踪过程进行了设计，而这有可能导致另一个状态量处于不确定状态，因此需要对另一个变量的状态进行分析，即对此系统进行内动态稳定性分析。

由式(2)得到

(15)

当按照式(9)、式(14)设计控制律后，x1最终趋于iLref。由式(15)可知，此时x2是一个保持有界的稳定值，因此该系统为内动态稳定性系统，所设计的控制律是合适的。

联立式(9)、式(14)，可以得到超级电容充电时的控制框图，如图2所示。

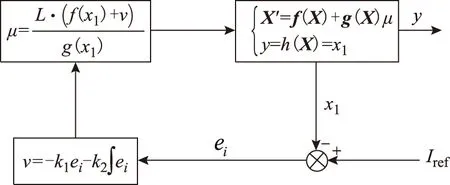
图2 超级电容充电模式下非线性控制框图Fig.2 Nonlinear control block diagram of the super capacitor in charging mode

3 超级电容放电算法设计

3.1 放电Boost电路建模

当超级电容为负载供电时，电路为Boost电路，开关管VT1恒关断、VT2采用恒频PWM调制，同样采用状态空间平均法对电路建模，得到电路的数学模型

(16)

式中，R为负载电阻值；uC为一个开关周期内负载侧电压平均值。

选取状态变量xl=iL、x2=uC，则可以得到以状态向量X=[x1，x2]表示的单输入仿射非线性系统的标准型

X′=f(X)+g(X)μ

(17)

式中

3.2 输入-状态精确线性化分析

放电时的Boost电路仍然是二阶系统，经验证，该系统满足输入-状态精确反馈线性化的条件。因此，同样考虑对由Boost电路所建立的仿射非线性系统进行输入-状态反馈精确线性化。

假设新构造状态变量为z1，根据式(4)、式(5)的条件，取新的状态变量

(18)

函数式(18)即为电路中电感和滤波电容的总储能函数，具有实际物理意义。

计算状态变换

(19)

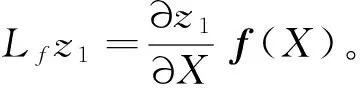
则可将原系统式(17)转换为以z1、z2表示的线性系统，即

(20)

式中，v为所要设计的新的控制律。通过对v的设计，可以对z1进行控制。

此时，原控制量为

(21)

式中

变量z1中包含负载电压和电感电流两个变量，系统的控制目标是控制系统达到稳态时的负载电压保持为uCref不变，而任意时刻电感电流值是随着超级电容端电压以及电路占空比的变化而变化的。因此，为了确定不同时刻z1的参考值，需先确定不同时刻电感电流的参考值。

当电路达到稳态时，根据一个周期内电路功率守恒得到

(22)

式中，负载电压uC=uCref。

在超级电容电压uSC不断下降的过程中，由式(22)可以确定任意时刻的电感电流iL值，即为电感电流参考值iLref。此时状态变量z1的参考值为

(23)

由式(20)、式(23)可知，通过设计合适的控制律v能保证新的状态变量z1跟踪z1ref，但实际需要的是z1中的变量x1跟踪iLref、x2跟踪uCref。

联立式(18)、式(22)、式(23)得到

(24)

通过Matlab对式(24)求解，一共可以得到4组解，然而只有一组xl=iLref、x2=uCref是符合实际电路情况的。因此，当z1跟踪z1ref时，就可以实现输出电压对参考电压的跟踪。原来对uC跟踪uCref的设计也就转为对新状态量z1跟踪z1ref的设计。

设误差量

e=z1-z1ref

(25)

(26)

(27)

选择新的控制量

v=-k1e-k2e′

(28)

式(28)中的参数k1、k2若选择适当，可以使系统式(20)为指数稳定的系统，且当系统稳定后能实现输出电压跟踪参考电压的目标。将式(28)代入式(21)中，即可得到对原来占空比函数μ的控制律。

联立式(17)、式(21)、式(28)可以得到超级电容放电时的控制框图，如图3所示。

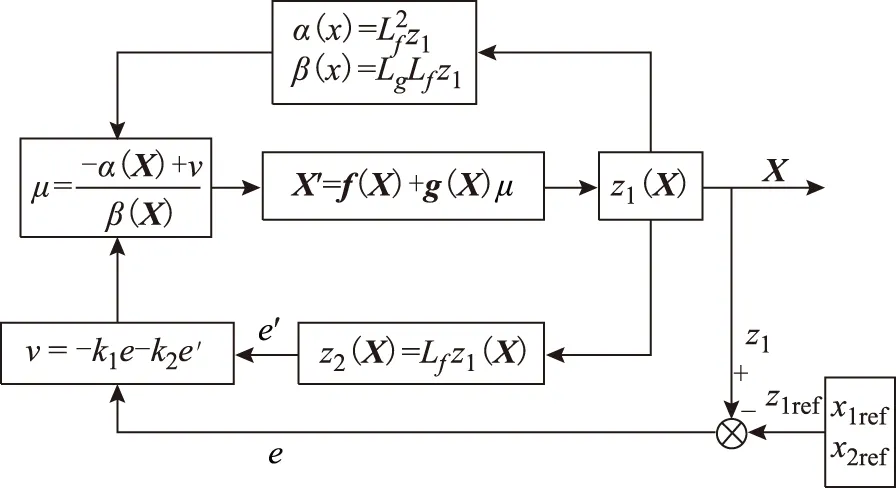
图3 超级电容放电模式下非线性控制框图Fig.3 Nonlinear control block diagram of the super capacitor in discharging mode

4 仿真及实验验证

4.1 一次电路仿真参数

为了验证本文所设计的超级电容充放电控制算法的控制效果，在Matlab/Simulink中搭建仿真模型进行验证。一次电路参数如下：

1)双向DC-DC充放电电路参数：电路电感L=0.6 mH，滤波电容C=1 100 μF，负载电阻R=2 Ω，IGBT开关频率fS=10 kHz。

2)超级电容参数：超级电容CSC=166 F，等效串联电阻RS=6 mΩ，等效并联电阻RP=2.5 kΩ。

4.2 控制算法参数讨论

电路中电感、电容的选取会对系统的动静态性能产生一定影响，当取值过大时，电流或电压的变化速度较慢，暂态时间较长；若取值过小，则会降低系统的稳定性，产生较大谐波。此外，控制系统中的参数也会对系统性能产生较大影响，下面具体分析控制参数如何整定。

在确定控制量之后，经过式(9)或式(21)直接计算得到了电路占空比，因此控制参数的取值不是无限制的，应能保证输入占空比取值范围在0～1之间变化。同时，为了保证控制量的引入能取得一定的控制效果，应使控制量大小与算法中其他项处于相同的数量级。

下面具体分析当控制量选取不同参数时对控制性能的影响，并进行仿真验证，以便给参数调整提供一定的依据。

充电时，k1代表误差量的增益，k2代表误差积分量的增益。当k1增大时，误差的作用将被放大，因此会使得系统动态速度加快，但过大会导致系统在稳态值附近振荡，k1变小则会导致动态速度变慢。由于误差积分量是对误差进行累积，因此该项的存在可以消除系统的稳态误差，但当k2过大时，会使系统超调严重，而当k2变小时，则会降低系统的响应速度。设定直流电源以48 V恒压向超级电容充电，控制充电电流为10 A。图4a、4b分别为k1、k2取不同值时电感电流的仿真波形。

图4 充电模式下不同参数时电感电流仿真波形Fig.4 Simulation waveform of inductor current with different parameters during the charging processes

放电时，k1代表电压电流的耦合项与稳态时电压电流耦合项的误差量的增益，k2代表功率不平衡量的增益。当k1增大或k2减小时，误差项的作用将变大，导致系统在未达到稳态时由于电压或电流某项超过稳态值而使得误差量为零，之后再经过振荡调节过程使电路达到功率平衡状态；当k1减小或k2增大时，功率不平衡量的作用将变大，使得系统首先保证功率平衡而使得动态响应速度变慢。设定超级电容初始电压30 V，控制负载侧2 Ω电阻的电压为50 V。图5a、5b分别为k1、k2取不同值时负载侧电压的仿真波形。

图5 放电模式下不同参数时负载电压仿真波形Fig.5 Simulation waveform of load voltage with different parameters during the discharging processes

由于放电时电感电流与负载电压之间不是相互独立的关系，因此本文设计的控制算法是对两者的耦合项进行控制，即是对系统整体的动静态性能进行控制，此时控制参数对电感电流与负载电压具有类似的作用效果，限于篇幅，电感电流的仿真波形图在此省略。

综上，可以看出，当参数选择不当时，可能会导致系统超调量过大或调节时间变长，严重时会使系统产生振荡。因此，应针对控制效果对参数进行微调以取得最优的控制性能。

通过分析比较，本文选取控制系统仿真参数为：充电时k1=10、k2=0.2；放电时k1=107、k2=103。

4.3 充电动态仿真

当超级电容的充电功率发生变化时，由于电容电压不能突变，因此控制算法应能迅速对超级电容的充电电流进行调整。为此针对超级电容充电电流变化的情况进行仿真验证。

设定充电时直流电源电压48 V恒定，充电电流参考值初始为10 A，在0.03 s和0.06 s时刻分别变为5 A 和10 A。图6为充电电流参考值发生变化时电感电流的动态响应波形。

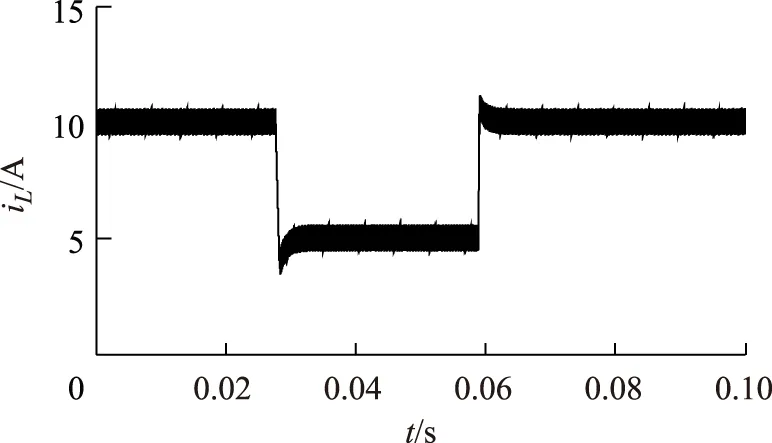
图6 充电电流变化时系统动态特性Fig.6 Dynamic response of the system when charge current change

从图6可以看出，非线性控制算法可以较好地控制电感电流跟踪参考值，没有静态误差，并且当参考电流发生变化时，电感电流可以较快地过渡到新的稳态值。

4.4 放电动态仿真

当超级电容作为电源向负载放电时，系统的目标是维持负载侧电压恒定，当负载突变时，控制算法应具有快速的动态响应速度，维持负载侧电压稳定。因此，针对负载突变的情况进行仿真验证。

设定超级电容的初始电压为30 V，由超级电容向2 Ω电阻放电，控制负载电压为50 V，在0.04 s和0.07 s时电阻分别突变为1 Ω和2 Ω。图7为负载侧电压的动态响应波形。

图7 负载突变时系统动态特性Fig.7 Dynamic response of the system when load change

从图7可以看出，当负载突变时，输出电压经过一个暂态后能够快速回到设定值。并且，即使超级电容端电压在放电过程中不断下降，非线性控制算法仍能维持负载侧输出电压为设定值不变。

4.5 实验参数

为了进一步验证本文所设计非线性控制算法的正确性及优越性，在硬件实验中同时比较非线性控制算法与双环PI控制算法之间性能的差异。基于TMS320F28335设计相关实验电路，进行实验验证。一次电路所选的参数与仿真时相同，其中，超级电容选择由NANOFORCE公司生产的型号为MPAK0101848651666BC超级电容，额定容量166 F，额定电压48 V，最高充放电电流650 A。主开关管选用FF450R17ME4型IGBT。由于实际硬件电路中的电感、电容、IGBT等器件存在附加阻尼及线路阻抗等一些不可忽略因素的影响，实验参数与仿真时有一定的差异。实验中的控制参数见表1和表2。

表1 非线性控制参数Tab.1 The parameters of nonlinear control algorithm

表2 PI控制参数Tab.2 The parameters of PI control algorithm

4.6 充电实验

设定充电时直流电源电压48 V恒定，对超级电容充电电流发生突变的情况进行实验验证。图8为分别采用PI控制算法和本文提出非线性控制算法时系统的电感电流动态响应波形。

由图8可以看出，当超级电容充电电流参考值发生变化时，两种算法均能控制电感电流快速跟踪参考电流，但非线性控制算法相较于PI控制算法具有更快的动态响应速度，更小的超调量。

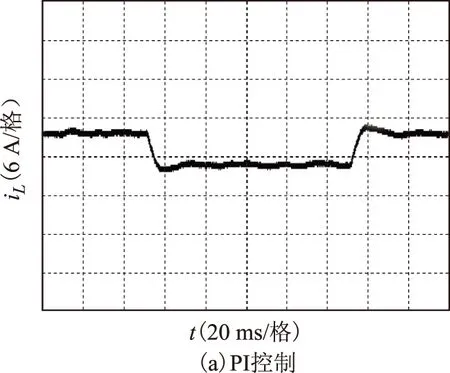
图8 充电电流变化时电感电流动态响应波形Fig.8 Dynamic response waveform of the inductor current when charge current change

4.7 放电实验

超级电容经过充电过程后电压达到20 V，此时由超级电容向负载放电，维持负载侧电压为30 V不变，针对负载突变的情况进行实验验证。图9为分别采用PI控制算法和非线性控制算法时系统的超级电容端电压、负载电压及电感电流的动态响应波形。

图9 负载突变时系统动态响应波形Fig.9 dynamic response waveform of the system when load change

从图9可以看出，当负载从轻载(R=4 Ω)跳变为重载(R=2 Ω)时，超级电容由于电容较大，因此电压没有明显变化，但负载侧电压均有一个瞬间的电压跌落，之后恢复至设定电压，同时，电感电流也将迅速由原来的状态过渡到新的稳态。但非线性控制算法相较于PI控制算法具有更短的调节时间，且输出电压和电感电流的波形更加平稳。

5 结论

本文针对超级电容储能系统设计了一种非线性控制算法，实现了超级电容恒流充电与恒压放电的控制目标，并通过仿真和实验进行了验证。通过实验结果可以看出，本文设计的控制算法具有以下优点：

1)该控制算法能够控制超级电容的充电电流和放电电压精确跟踪给定值，无稳态误差。

2)通过该算法与PI算法的比较可以看出，在超级电容储能系统中采用非线性控制算法能明显提高系统的动态响应速度，减小超调量。

3)该控制算法只含有2个需要整定的参数，相比于传统双环PI控制算法中的4个PI参数而言，参数整定更容易实现。

4)该算法可以推广到对电力系统中其他非线性系统的控制设计中，具有实际意义。

[1] Arani M F M，El-Saadany E F.Implementing virtual inertia in DFIG-based wind power generation[J].IEEE Transactions on Power Systems，2013，28(2)：1373-1384.

[2] 王成山，武震，李鹏.微电网关键技术研究[J].电工技术学报，2014，29(2)：1-12. Wang Chengshan，Wu Zhen，Li Peng.Research on key technologies of microgrid[J].Transactions of China Electrotechnical Society，2014，29(2)：1-12.

[3] 姚莉娜，杨东海，段运鑫，等.微电网离网运行有功缺额计算方法[J].电力系统保护与控制，2015，43(15)：137-144. Yao Lina，Yang Donghai，Duan Yunxin，et al.A calculation method of active power shortage in off-grid microgrid[J].Power System Protection and Control，2015，43(15)：137-144.

[4] 邱麟，许烈，郑泽东，等.微电网运行模式平滑切换的控制策略[J].电工技术学报，2014，29(2)：171-176. Qiu Lin，Xu Lie，Zheng Zedong，et al.Control method of microgrid seamless switching[J].Transactions of China Electrotechnical Society，2014，29(2)：171-176.

[5] 郭芳，邓长虹，廖毅，等.功率平滑用电池储能系统的功率响应特性研究[J].电工技术学报，2015，30(12)：434-440. Guo Fang，Deng Changhong，Liao Yi，et al.Research on the response characteristics of BESS used in power smoothing[J].Transactions of China Electrotechnical Society，2015，30(12)：434-440.

[6] 张蕴昕，孙运全.混合储能在风光互补微网中的控制策略[J].电力系统保护与控制，2015，43(21)：93-98. Zhang Yunxin，Sun Yunquan.Control strategy of a hybrid energy storage in wind-solar hybrid generation micro-grid[J].Power System Protection and Control，2015，43(21)：93-98.

[7] 何金梅，郑雪梅，王卫，等.Boost变换器混沌现象的非奇异终端滑模控制方法[J].电工技术学报，2013，28(4)：104-108，132. He Jinmei，Zheng Xuemei，Wang Wei，et al.Terminal sliding mode control of Boost converter with chaos[J].Transactions of China Electrotechnical Society，2013，28(4)：104-108，132.

[8] 程启明，程尹曼，薛阳，等.三相电压源型PWM整流器控制方法的发展综述[J].电力系统保护与控制，2012，40(3)：145-155. Cheng Qiming，Cheng Yinman，Xue Yang，et al.A summary of current control methods for three-phase voltage-source PWM rectifiers[J].Power System Protection and Control，2012，40(3)：145-155.

[9] 张明锐，李元浩，欧阳丽，等.基于混杂系统DC-DC变换器的永磁风电并网系统直流母线电压稳定控制[J].电工技术学报，2015，30(4)：62-69. Zhang Mingrui，Li Yuanhao，Ou Yangli，et al.DC bus voltage stability control of DC-DC converter in the permanent magnet wind power grid-connected system based on the hybrid system[J].Transactions of China Electrotechnical Society，2015，30(4)：62-69.

[10]帅定新，谢运祥，王晓刚，等.Boost变换器非线性电流控制方法[J].中国电机工程学报，2009，29(15)：15-21. Shuai Dingxin，Xie Yunxiang，Wang Xiaogang，et al.Nonlinear current control method for boost converter[J].Proceedings of the CSEE，2009，29(15)：15-21.

[11]王楠，李永丽，张玮亚，等.飞轮储能系统放电模式下的非线性控制算法[J].中国电机工程学报，2013，33(19)：1-7. Wang Nan，Li Yongli，Zhang Weiya，et al.A nonlinear control algorithm for flywheel energy storage systems in discharging mode[J].Proceedings of the CSEE，2013，33(19)：1-7.

[12]Ding Guanyu，Alexis Kwasinski.Digital constant on-time controlled Multiple-input buck and buck-boost converters[C]//28th Annual IEEE Applied Power Electronics Conference and Exposition (APEC)，Long Beach，CA，2013：1376-1382.

[13]蒋玮，陈武，胡仁杰，等.光伏发电系统中超级电容器充电策略[J].电力自动化设备，2014，34(12)：31-37. Jiang Wei，Chen Wu，Hu Renjie，et al.Charging Strategy for super capacitor of photovoltaic generation system[J].Electric Power Automation Equipment，2014，34(12)：31-37.

[14]Abdeladim G，Sarath T.Modelling of super capacitor modules and parameters extraction[C]//Proceedings of 46th International Universities’ Power Engineering Conference (UPEC)，Soest，Germany，2011：1-6.

[15]赵亚杰，夏欢，王俊兴，等.基于动态阈值调节的城轨交通超级电容储能系统控制策略研究[J].电工技术学报，2015，30(14)：427-433. Zhao Yajie，Xia Huan，Wang Junxing，et al.Control strategy of ultra capacitor storage system in urban mass transit system based on dynamic voltage threshold[J].Transactions of China Electrotechnical Society，2015，30(14)：427-433.

[16]Middlebrook R，Cuk S.A general unified approach to modelling switching-converter power stages[C]//IEEE Power Electronics Specialists Conference，1976：18-34.

[17]李啸骢，程时杰，韦化，等.输出函数在单输入单输出非线性控制系统设计中的重要作用[J].中国电机工程学报，2004，24(10)：52-58. Li Xiaocong，Cheng Shijie，Wei Hua，et al.Important effection of the output function in SISO nonlinear control system design[J].Proceedings of the CSEE，2004，24(10)：52-58.

[18]贺昱曜，闫茂德.非线性控制理论及应用[M].西安：西安电子科技大学出版社，2002.

[19]Kim Marn-Go.Error amplifier design of peak current controlled (PCC) Buck LED driver[J].IEEE Transactions on Power Electronics，2014，29(12)：6789-6795.

Nonlinear Control Algorithm for Super Capacitor Energy Storage System Based on Exact Linearization Theory

Li Xuan Li Yongli Chang Xiaoyong

(Key Laboratory of Smart Grid of Ministry of Education Tianjin University Tianjin 300072 China)

In view of the nonlinear characteristics of super capacitors and DC-DC converters，a nonlinear control algorithm for the super capacitor energy storage system is designed.Through the analysis on working states of the circuit，the affine nonlinear model is established.The relationship between the circuit state and the duty cycle is deduced by using the exact feedback linearization theory.Furthermore，the control algorithm is designed and its stability of internal dynamics is proved.Then the control targets of charging with constant current and discharging with constant voltage are achieved.Simulation model is constructed in the Matlab/Simulink platform.The effectiveness of the control algorithm is confirmed.Then，the difference between the nonlinear control algorithm and the PI control method is compared by experimental circuit building in laboratory.Results show that，compared with the traditional PI algorithm，using nonlinear control law in the super capacitor energy storage system can significantly improve dynamic performance and ensure stability.

Super capacitor，energy storage system，nonlinear control，state variables feedback，exact linearization

国家重点基础研究发展计划(973计划)(2009CB219704)、国家自然科学基金(51177108)和高等学校博士学科点专项科研基金(20110032110066)资助项目。

2015-06-04 改稿日期2015-09-21

TM46

李 轩 男，1990年生，硕士研究生，研究方向为电力系统保护与控制。

E-mail：lixuanyeah@126.com(通信作者)

李永丽 女，1963年生，教授，博士生导师，研究方向为电力系统保护与控制。

E-mail：lyltju@163.com