楼内配变室砼地板结构振动声辐射分析
2016-12-27徐禄文高芳清
徐禄文,梁 林,高芳清,吴 祺
(1.国网重庆市电力公司 电力科学研究院,重庆 401123;2.西南交通大学 力学与工程学院,成都 610031)
楼内配变室砼地板结构振动声辐射分析
徐禄文1,梁 林2,高芳清2,吴 祺2
(1.国网重庆市电力公司 电力科学研究院,重庆 401123;2.西南交通大学 力学与工程学院,成都 610031)
楼内配变设备(例如变压器)工作时会引起与之相连的混凝土地板振动,并通过传递引起其它结构振动,这些振动会产生结构声辐射现象。对此进行分析为楼内配变室结构传声研究的一部分工作,假定砼地板四边固支并适当考虑地基的弹性作用,采用Hamilton方程和振型叠加法对地板的振动位移方程进行了推导与求解,并据此对地板的结构声辐射进行研究。其中注意到振动模态对结构声辐射功率贡献的非独立性,计入结构振动模态耦合项的影响,对地板的结构声辐射效率与声功率进行分析。
振动与波;变压器;混凝土地板;振动模态;结构声辐射;声功率
办公或居民楼内设置配变室已很常见,配变设备(变压器)常安置于砼地板上,设备运转激起地板振动[1-3],向外传递并产生结构声辐射[4-6],该噪声作为环境污染影响人们的日常生活,为此掌握相关结构的振动性状以及其对外声辐射规律具有现实意义。板结构(包括砼板结构)的受迫振动及其传递,已有大量前人研究成果,目前常用的研究方法,主要分数值方法和能量法,数值方法主要包括有限元法(FEM)[7-8]、边界元法(BEM)[9-10],其中有限元法对于高频分析存在相对较大的误差;能量法对于位移函数的准确选取较为困难。考虑上述因素以及文中砼地板安置于弹性地基上且与四面墙体固结,本文基于温克勒(Winkler)地基模型适当考虑了地基的弹性支持作用,建立了楼内配变室混凝土地板结构动力分析模型,结合Hamilton原理和振型叠加法对混凝土板的位移方程进行详细的推导,据此在板的位移方程求解的基础上,对板的结构声辐射进行研究。结构声辐射效率和声功率是评价结构振动声辐射能力的重要指标,Wallace在70年代就提出关于简支板的模态辐射效率[11-12]的计算方法,后续众多学者对不同边界条件板结构的声辐射效率和声功率也进行了研究,特别是考虑到各阶结构模态对声功率的贡献互相不独立[13-15],总的声功率并不是等于各个单独结构模态组成的声功率之和,而是等于各个独立模态声功率加上各阶模态之间的耦合声功率。因此本文在考虑结构模态之间的耦合项的前提下,对室内配电房变压器振动所致弹性地基上地板的声辐射进行研究。
1 地板在弹性地基上的理论模型
如图1所示,将变压器在地板上激振情况简化为如下板结构分析模型,变压器激励简化为集中简谐激振力配电房地板与四面墙体固结,因此考虑地板的边界条件为四边固支情况。又考虑到板置于弹性地基上,将地基简化为刚度为K0的弹簧,不考虑弹性地基阻尼,K0为地基竖向刚度系数动力解,与地基土的力学参数有关,其计算式如下
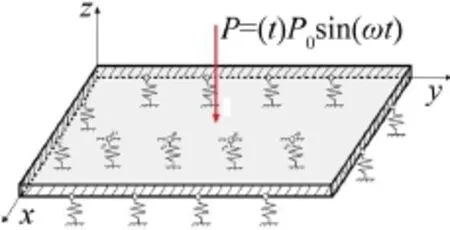
图1 混凝土板简化结构示意图
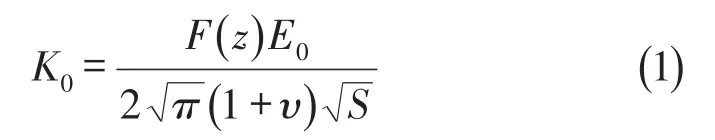
混凝土板在变压器激振下振动,设板振动的总势能为V,地基的弹性势能为V0,T表示混凝土板振动时的总动能,W表示外力做功,其与位移的关系表达式如下
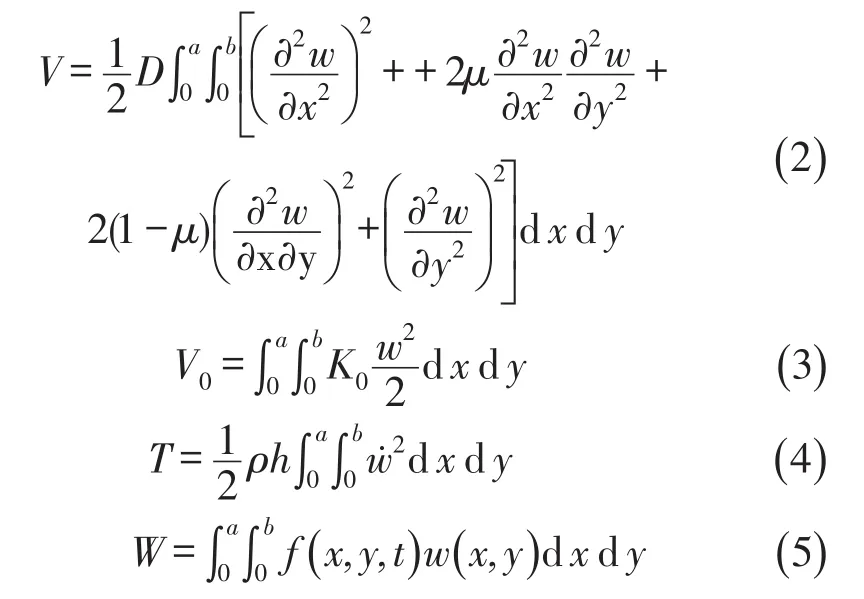
式中w表示挠度,ρ为混凝土板密度,μ为其泊松比,h为其厚度,K0为地基弹性刚度。表示弯曲刚度,f(x,y,t)表示施加在混凝土板上的荷载分布函数,变压器的激振按照点激励来计算。
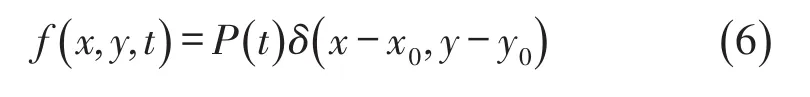
2 地板的Hamilton方程及位移函数
2.1 混凝土板的Hamilton方程
通过弹性力学可知,混凝土板的Hamilton方程为

代入哈密顿方程可得
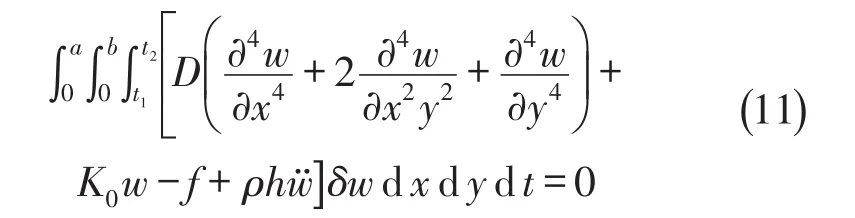
从而得到微分方程为
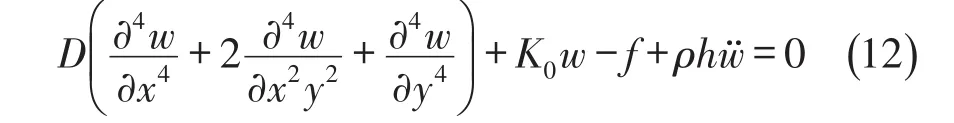
2.2 混凝土板位移函数的求解
在微分方程式(12)的基础上,利用振型叠加法求板的位移方程,将混凝土板的位移方程按正则振型Wi,j展开成如下的级数
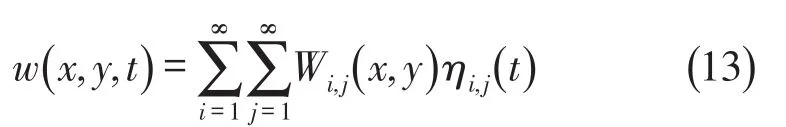
其中ηi,j(t)为主坐标,将上式代入式(12)求出的振动微分方程中可得
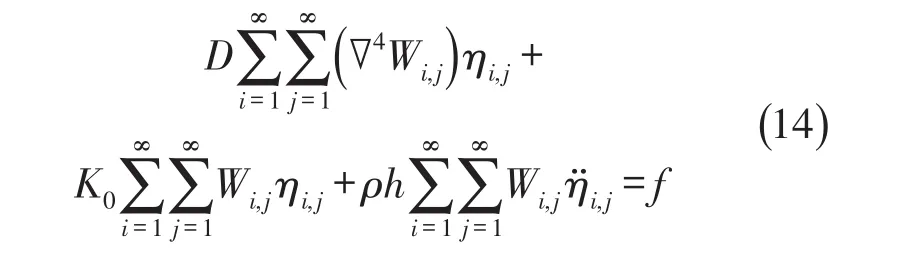
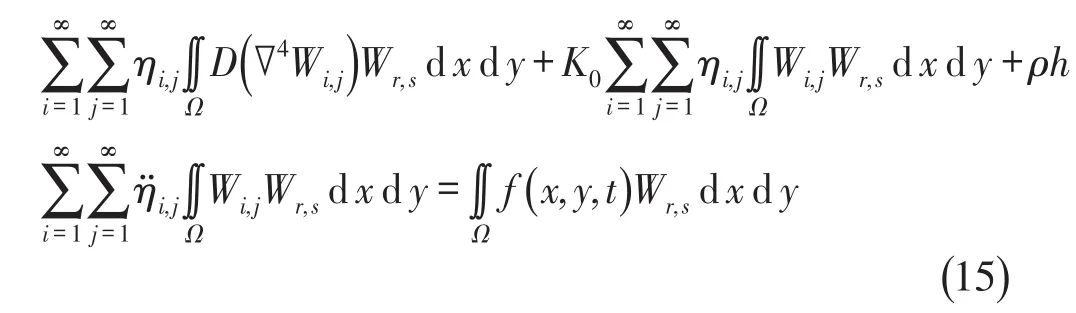
由主振型之间的正交性条件,上式可化简为

对于Wi,j(x,y)可通过有限积分变换,得
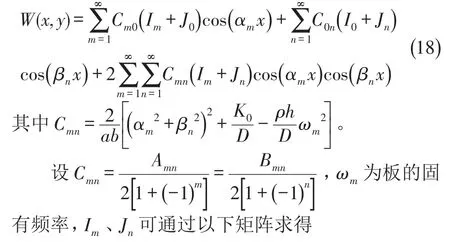

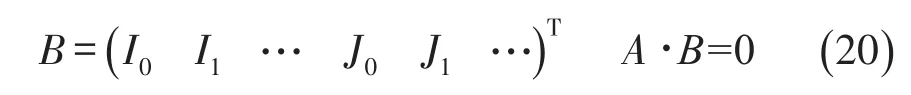
通过上述计算便可得到混凝土板在弹性地基上的位移方程以及混凝土板的固有频率。
3 变压器振动所致地板的声辐射分析
3.1 地板辐射声功率
设地板表面振动法向速度为V(x,y),上面已对地板受迫振动的位移方程进行了详细推导和求解,要得到V(x,y)只需要将位移方程对t求一次偏导便可,现将V(x,y)通过结构模态进行展开,并以矩阵形式表示如下

声功率的表达式如下

式中C为声功率传递矩阵,是实对称正定矩阵,矩阵的第(mn,m′n′)阶元素为
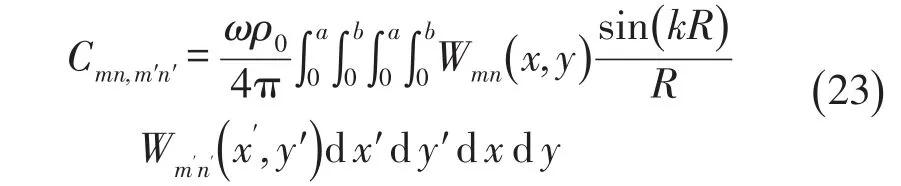
式中ω为激振频率,ρ0为空气密度,a和b分别表示地板的长和宽,k为波数,为声音速度,传递矩阵C中的Cmn,mn为矩阵中的对角元素,表示第阶模态对声功率的贡献。非对称元素Cmn,m′n′表示的是第阶和阶模态之间耦合对声功率的贡献。由于传递矩阵的对称性,所以有Cmn,m′n′=Cm′n′,mn。
3.2 地板声辐射效率A
矩形地板声辐射效率的定义式如下
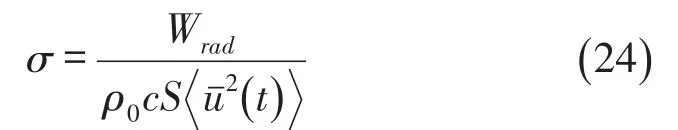
式中S表示矩形地板的面积表示矩形地板的表面法向速度的空间均方,其中右上角的“H”表示共轭转置。
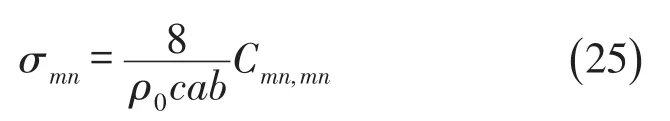
通过式(22)和式(25)可知,想要知道变压器致地板振动的声功率和声辐射效率,最主要的是要求得其声功率传递矩阵,而式(23)关于传递矩阵的计算是一个四重积分,计算相当麻烦,下面给出了在考虑振动模态间耦合项的前提下,地板振动声功率传递矩阵更为简单的解,式(26)-式(29)为传递矩阵中各元素的解析解
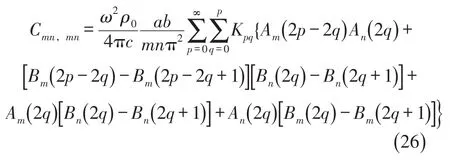

上式看上去比较复杂,但通过计算机计算该传递矩阵是非常方便的,并且只有当(m,n)和(m′,n′)都同为(奇,奇)、(奇,偶)、(偶,奇)、(偶,偶)中的一组时,传递矩阵元素才非零。
4 数值计算
变压器置于室内配电房地板上,地板长a=5 m ,宽b=5 m ,厚度h=0.1 m ,板密度ρ=3 000 kg/m3,E=300 GPa,μ=0.2,地基的刚度系数K0=5 MPa/mm,声速c=340 m/s,空气密度ρ=1.29 kg/m3。
为了更精确地得到变压器激起板振动而产生的声辐射数值计算结果,考虑模态耦合项的影响因素,对声功率和声辐射效率进行计算。而在对此进行分析前先对模态耦合项对计算分析的影响大小做分析,图2(a)-图2(d)分别描述了(m,n)和(m′,n′)都同为(奇,奇)、(奇,偶)、(偶,奇)、(偶,偶)时耦合项的影响因子ζ随无量纲频率ka的变化曲线图,图中纵坐标影响因子
从图2可以看出,在低频时,模态耦合项的影响因子较大,不能被忽略,随着频率的升高,耦合项的影响相对趋于零,且当(m,n)和(m′,n′)都同为(奇,偶)或(偶,奇)时,耦合项的影响就更为显著,另外,图2(a)-图2(d)中均存在影响因子为负数的情况,造成此类情况的原因不仅跟模态之间耦合项的正负有关,同时与变压器的置放位置即激振力的激振位置和相位都是相关的。总的来说,如果分析无量纲频率达到了较大的值如ka≥35,是可以忽略耦合项的影响,本文主要对变压器激振引起地板的声辐射进行分析,图3为对配电房地板的信号检测而得到配电房地板的加速度时程曲线及频谱图,从图中可以看出变压器典型激励频率有100 Hz、200 Hz、300 Hz、400 Hz。而代入计算得到的无量纲频率分别为1.47、2.94、4.41、5.88,因此对典型的变压器激振环境而言,对地板的声辐射进行分析研究应该考虑模态之间耦合项的影响。
为了说明模态耦合项对砼地板声功率的影响,考虑典型变压器振动环境,在砼地板中心即(2.5 m,2.5 m)处进行激励,得到的声功率曲线如图4所示,其中红色实线为忽略耦合项的计算结果,蓝色实线为考虑耦合项的计算结果。
通过图4可以看出模态耦合项对声功率有着一定的影响,且在低频段表现较为明显。因此,为了得到声功率更为精确的解,有必要考虑模态耦合项对砼地板辐射声功率的影响。
变压器不同放置位置对砼地板辐射声功率显然是有影响的,在考虑模态耦合项对辐射声功率影响的前提下分别对变压器置于地板对角线上的A、B、C三点进行分析,其座标分别为A(1 m,1 m)、B(2 m,2 m)、C(2.5 m,2.5 m),通过分析,得到变压器在以上三点激励时砼地板辐射声功率曲线的对比图,如图5所示。
由图5可以看出在不同点激励时砼地板声功率是有所差别的,离地板中心越近,辐射声功率越大,远离中心越小,虽然三者有所差别,但是在变化趋势上还是有着相似的规律性。因此在变压器布置时应尽量远离地板中心。
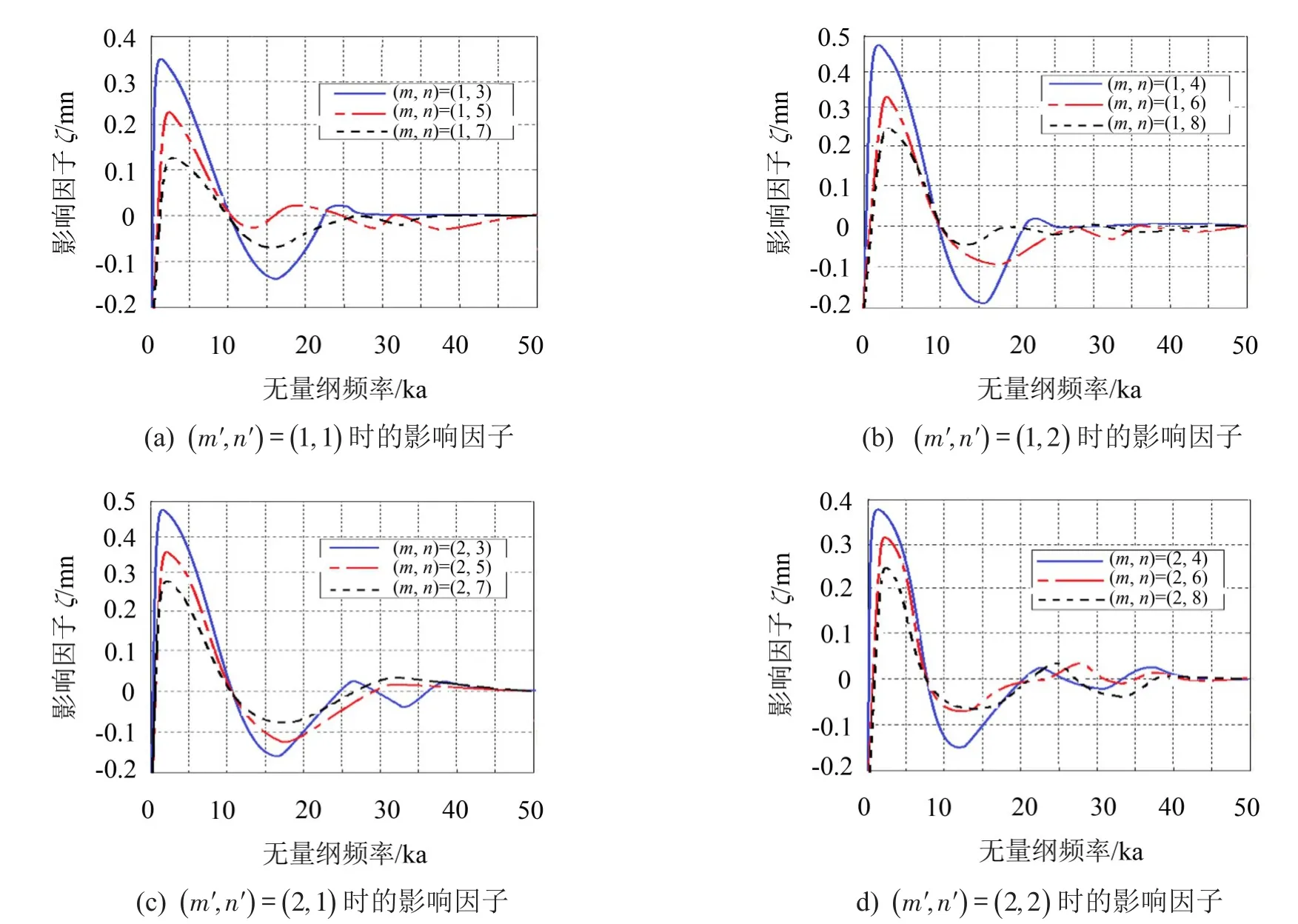
图2 影响因子随无量纲频率的变化曲线图

图3 配电房地板加速度时程曲线及频谱图
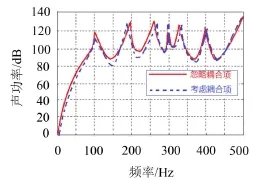
图4 中心点激励砼地板声功率曲线
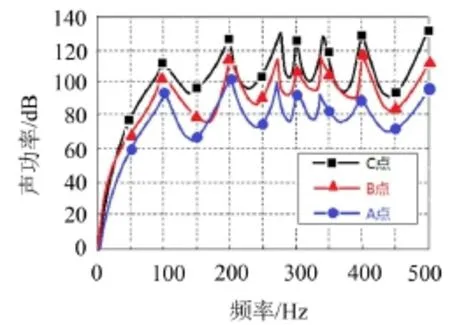
图5 不同激励点的声功率曲线
5 结语
变压器在配电房中振动,使地板随之发生受迫振动,通过建立分析模型结合Hamilton原理和振型叠加法对板的受迫振动进行详细的计算分析,得到其振动位移方程。在位移方程的基础上,对砼地板的辐射声功率进行分析,不仅给出了声功率传递矩阵各个元素较为简单的计算方法,同时也考虑了模态之间耦合项对声功率的影响因素,在此基础上得到了模态耦合项影响因子的变化曲线,揭示了模态耦合项在不同频率下对声功率的影响大小。在考虑模态耦合项的情况下得到变压器在不同点激振时的声功率曲线,发现距离地板中心越近,相应的辐射声功率会越大,因此在变压器布放时应尽量避开中心位置。
[1]MUKHERJEE M.Forced vertical vibrations of an elastic elliptic plate on an elastic half space a direct approach using orthogonal polynom-ials[J].International Journal of Solids and Structures,2001,38:389-399.
[2]C W LIM,C F LU,Y XIANG,et al.On the new symplectic elasticity approach for exact free vibration solutions of rectangular Kirchhoff plates[J].International Journal of Engineering Science,2009(1):131-140.
[3]姚伟岸,蔡智宇,胡小飞.矩形正交各向异性薄板弯曲受迫振动问题的分析解[J].动力学与控制学报,2011(1):12-17.
[4]MAIDANIK G.Response of ribbed panels to reverberant acoustic fields[J].Journal of the Acoustical Society of America,1962,34:809-826.
[5]CURREY M N,CUNEFARE K A.The radiation modes of baffled finite plates[J].Journal of the Acoustical Society ofAmerica,1995,98:1570-1580.
[6]CUNEFARE K A.The radiation efficiency grouping of free-space acoustic radiation modes[J].Journal of the Acoustical Society ofAmerica,2001,109:203-2312.
[7]吴鸿庆,任侠.结构有限元分析[M].北京:中国铁道出版社,2000:321-424.
[8]陈伟,何飞.基于结构参数化的有限元分析方法[J].机械科学与技术,2003(6):945-950.
[9]杨德全,赵忠生.边界元理论及应用[M].北京:北京理工大学出版社,2002:1-317.
[10]JASWON M A,MAITI M.An integral equation of plate bending problems[J].JournalofEngineering Mathematics.1968(1):83-93.
[11]WALLACE C E.Radiation resistance of a rectangular panel[J].Journal of the Acoustical Society of America, 1972,51(5):946-952.
[12]向伟,丁渭平,吴昱东.模态辐射效率在微车低频轰鸣问题中的应用[J].噪声与振动控制,2015,35(5):2-4.
[13]CURREY M N,CUNEFARE K A.The radiation modes of Baffled finite plates[J].Journal of the Acoustical Society ofAmerica,1995,98(3):1570-1580.
[14]LI W L,GIBELING H J.Acoustic radiation from a rectangularplate reinforced by springsatarbitrary locations[J].Journal of Sound and Vibration,1999,220 (1):117-133.
[15]朱拥勇,刘宝.简支矩形板在空气与水中声辐射特性比较[J].噪声与振动控制,2016,36(3):2-5.
Structural Vibration and Sound RadiationAnalysis of the Concrete Floor of Indoor Substations
XU Lu-wen1,LIANG Lin2,GAO Fang-qing2,WU Qi2
(1.Electric Power Science Research Institute,State Grid Chongqing Electric Power Company, Chongqing 401123,China; 2.School of Mechanics and Engineering,Southwest Jiaotong University,Chengdu 610031,China)
Operation of indoor substations(e.g.transformers)in buildings can induce adjacent concrete floor vibration, which can be transferred to the other portions of the building structure and cause the structure-borne sound radiation.In this paper,the structure-borne sound radiation induced by the indoor substations is studied.The concrete floor is simplified to an elastic plate with the four sides simply supported laid on the elastic foundation.The vibration displacement equations of the floor are derived and solved using the Hamilton equation and the modal superposition method.Accordingly,the structureborne sound radiation is studied.It is noticed that the contribution of the vibration modes to the structure-borne sound radiation is not individual.Thus,the influence of the coupling terms of the structural vibration modes is considered for analyzing the radiation efficiency of the structure-borne sound and the sound power of the concrete floor.
vibration and wave;transformer;concrete floor;vibration mode;structure-borne sound radiation;sound power
O422.6
:A
:10.3969/j.issn.1006-1335.2016.06.024
1006-1355(2016)06-0121-05+191
2016-06-08
国网重庆电力公司科学技术研究项目(2014H01580)
徐禄文(1968-),男,四川省广安市人,高级工程师,主要从事电网电磁环境与噪声振动控制研究。E-mail:xuluwen023@qq.com
