矩形永磁铁的磁力计算及其应用

柴 凯，杨庆超，朱石坚，楼京俊

（1.海军工程大学 动力工程学院，武汉 430033；2.海军工程大学 船舶振动噪声重点实验室，武汉 430033）

矩形永磁铁的磁力计算及其应用

柴 凯1，杨庆超2，朱石坚2，楼京俊2

（1.海军工程大学 动力工程学院，武汉 430033；2.海军工程大学 船舶振动噪声重点实验室，武汉 430033）

负刚度结构可用于系统的低频隔振，依据等效磁荷法建立矩形永磁铁的磁力和刚度解析模型，得到实现负刚度的最优磁铁布置和充磁方向，并设计三磁体型准零刚度隔振系统。仿真结果表明，矩形磁铁磁力和刚度计算模型准确，三磁体型准零刚度隔振器在不影响载荷性能的前提下具有优越的低频隔振性能。

振动与波；矩形磁铁；负刚度；准零刚度；低频隔振

机械设备振动是潜艇辐射噪声的主要来源，隔振是控制振动向艇体传递的常用手段。降低固有频率和实现共振峰附近振动的高效隔离是提高隔振系统性能的关键[1]，传统的方法是通过降低系统刚度，但较低的刚度会使弹簧的静态位移增大，导致系统的承载能力降低。准零刚度隔振器是通过合理选择负刚度机构的几何和刚度参数，将正负刚度弹性元器件并联在静平衡位置附近获得零刚度的组合隔振器，系统的承载力由正刚度弹簧决定，负刚度元件用以减少系统动刚度，高静低动的特性能有效解决低频隔振下稳定性和隔振效果之间的矛盾，并显著扩大了隔振频带范围[2]。准零刚度隔振技术实现的关键在于负刚度机构的设计和计算，基于永久磁铁或电磁铁的负刚度机构因为无机械摩损、噪声小、无需润滑、可引入半主动控制调节系统刚度和承载能力不受负刚度机构影响等优点，引起了诸多学者的极大关注。Zhou等将结构梁、电磁铁和永久磁铁并联设计了隔振器，通过调节电流的方向实现隔振器的半主动控制[3]；Li等通过磁环与橡皮膜结合设计了负刚度隔振器[4]；Tao等设计了六自由度的磁悬浮型准零刚度隔振系统[5]；Shan等利用气囊和磁环结合设计了一种新型空气弹簧减振器[6]；Zheng等对基于永磁铁和电磁铁的准零刚度隔振器进行了深入研究[7]；Yu等采用垂直线性线圈弹簧和两个对称的磁力弹簧组合设计了磁力准零刚度隔振器[8]。但上述文献主要采用环形磁铁，文中通过建立矩形磁铁的磁力和刚度解析模型，并分析其负刚度特性，通过仿真优化矩形磁铁的布置方式、充磁方向和尺寸参数，将其应用于三磁体型准零刚度隔振器。

1 矩形磁铁的磁力解析模型

1.1 点磁荷磁场强度的计算

对于面积为2a×2b矩形磁面，见图1，磁荷面密度为σ，依据等效磁荷理论[9]，任意一点P的标量磁位的二维泊松方程

图1 矩形磁面对P点的磁标量势

其中Ui=x-(-1)ia，Vj=y-(-1)jb，W=z，

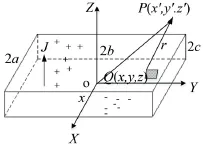
图2 矩形磁体对P点的磁标量势

对于体积为2a×2b×2c矩形磁铁，被磁化后各磁偶极子在磁铁内部均匀排列，N，S极首尾相连，只在两个端面出现单一的正或负磁荷，见图2。由静磁学理论[10]，当充磁方向与磁铁表面法线重合，钕铁硼永磁材料的介质极化强度J、面磁荷密度σ和剩余磁感应强度Br三者相等，令Wk=-(-1)kc，根据H=- φP，在场点P对φP求梯度，可得P点磁场强度

其中εx=ln(r-V)，εy=ln(r-U)，

1.2 矩形磁铁的磁力和刚度解析模型

设上下磁铁均均匀充磁，下磁铁尺寸为2a×2b×2c，介质极化强度为J，所在坐标系为O-XYZ；上磁铁尺寸为介质极化强度为方向与下磁铁相同，所在坐标系为坐标原点为见图3。

图3 上下矩形磁铁的几何模型

根据等效磁荷理论，两块磁铁间的磁力由上、下磁铁的上、下端面相互作用产生，两块充磁方向平行的静磁能

当上下磁铁充磁方向相同时F取正，反之则F取负，省略多重求和为零的项，可得

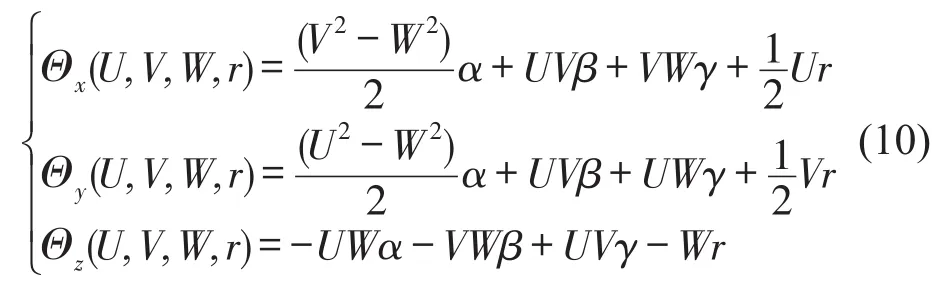
其中α=ln(r-U)，β=ln(r-V)，刚度可表示为力对位移的负导数，对式(10)分别在不同方向求导，并省略多重求和为零的项，可得

其中τx=Ulnβ+r，τy=Vlnα+r，τz=-2r-Ulnβ-Vlnα。

2 磁铁布置方式和充磁方向的选择

由上述分析可知，矩形磁铁磁力与磁铁的相对位置、磁铁充磁方向、磁铁几何参数和剩余磁感应强度等密切相关。

实现准零刚度隔振器的负刚度曲线应满足平衡位置某个邻域内刚度小于零，关于平衡位置两边对称且可微，且对于曲线2而言，由于负刚度系统不稳定，还应将其位移控制在-a和a之间，如图4所示。

图4 负刚度的特征曲线

研究矩形磁铁的负刚度机构的相对安装位置和充磁方向条件。设三块磁铁的尺寸均为20 mm×20 mm×10 mm，磁铁上下间隔h=20 mm，磁铁左右间隔l=30 mm，根据磁铁相对位置和充磁方向不同，分以下情况对中间磁铁的刚度进行分析。

图5(a)中三块磁铁沿Z轴间隔h布置，充磁方向相同，两两之间的磁力表现为吸引力。当上、下磁铁固定，中间磁铁沿Z轴上下运动时，kz=Kz(0,0,z-h)+Kz(0,0,z+h)，刚度曲线如图6(a)所示，满足负刚度曲线特征，但有位移限制；沿Y轴左右运动时，ky=2Ky(0,y,h)，刚度曲线见图6(b)，具有正刚度特性，需将中间磁铁的充磁方向改为垂直向下；沿X轴前后运动时，kx=Kx(x,0,h)=Ky(0,y,h)，也需将中间磁铁的充磁方向改为垂直向下后才能用于准零刚度隔振器的设计。

图5 矩形磁铁的布置方式

图6 垂直布置结构的刚度-位移曲线

图5(b)中三块磁铁沿Y轴间隔l布置，充磁方向两边磁铁相同，中间磁铁与两边磁铁相反。中间磁铁沿Z轴上下运动时，磁铁kz=-2Kz(0,l,z)，刚度曲线见图7(a)，具有正刚度特性，需将中间磁铁充磁方向改为垂直向上；沿Y轴左右运动时，ky=-Ky(0,y+l,0)-Ky(0,y-l,0)，刚度曲线见图7(b)，具有负刚度特性，但有位移限制；沿X轴前后运动时，kx=-2Kx(x,l,0)，刚度曲线见图7(c)，具有正刚度特性，需将中间磁铁的充磁方向改为垂直向上，才能用于准零刚度隔振器的设计。

综上分析，充磁方向平行时可用于准零刚度隔振器设计的组合有六种，如图8所示。

3 磁铁的尺寸优化

以图8中组合1为例，探究磁铁间距和磁铁几何尺寸对负刚度曲线的影响。由图9可知，h过大会导致刚度较小，无法抵消正刚度，不能降低系统固有频率；h过小会导致负刚度非线性特征增大，无法与正刚度匹配，分析中给定h=20 mm。为了在具有较大负刚度的同时还有较好的线性特征，磁铁组在X或Y方向可以并联布置，相应方向上尺寸应较小，假设X方向并联，故可将中间磁铁尺寸定为10 mm×30 mm×15 mm。

图7 垂直布置结构中的刚度-位移曲线

图8 不同矩形磁铁的负刚度结构组合

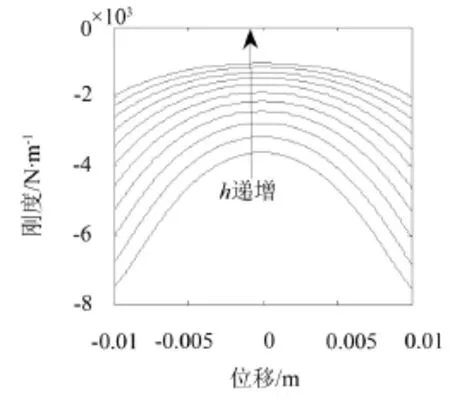
图9 不同h下的刚度曲线

为了使结构紧凑，设上下磁铁尺寸相同且满足a＞5 mm，b＞15 mm，c＜7.5 mm，下面依次分析a、b和c的变化对Z向刚度的影响。令b=20 mm，c=6 mm，a在6mm-12 mm内间隔0.5取值，由图10(a)可知，刚度随着a的增加而减小，线性特征变好，但当a超过9 mm后，刚度减小但线性改善程度并不明显，故取a=9 mm。令a=9 mm，c=6 mm，b在16 mm-22 mm内间隔0.5取值，由图10(b)可知，刚度随着b的增加而减小，线性特征变好，但当b超过20 mm后，刚度减小但线性改善程度并不明显，故取b=20 mm。令a=9 mm，b=20 mm，c在1 mm-7 mm内间隔0.5取值，由图10(c)可知，刚度随着c的增加而增加，线性特征变化程度较小，取c=5 mm。

4 基于三磁体的准零刚度隔振器设计

基于磁引力的三磁体型准零刚度隔振器原理如图11所示，永磁铁C1和C3固定于基座上，中间磁铁C2与隔振质量块相连，通过约束使其只能上下运动，C2和C1、C3呈吸引力布置。设M=2.5 kg，K=600 N/m，三块永磁铁的充磁方向相同，上下磁块尺寸为18 mm×40 mm×10 mm，中间磁块尺寸为10 mm×30 mm×15 mm，Br=1.1 t，μr=1.05 t，h=30 mm。

图12是三磁体Maxwell有限元仿真结构图。由图13可知，C2在平衡位置所受磁力为0，故将C2与质量块连接不会影响弹簧的载荷性能；三磁体组成的负刚度元件能产生与载荷位移相同的力，使得系统的回复力和刚度减小；有限元仿真结果与三磁体磁力解析模型结果吻合较好，验证了文中采用磁力解析模型的准确性。由图14可知，通过正负刚度的并联，使得系统在位移区间-10 mm和10 mm内总刚度趋于0，从而能在小幅振动范围内达到系统稳定以实现低频隔振。

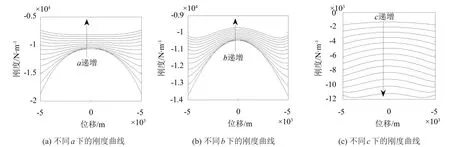
图10 尺寸参数对负刚度的影响

图11 三磁体型准零刚度隔振器

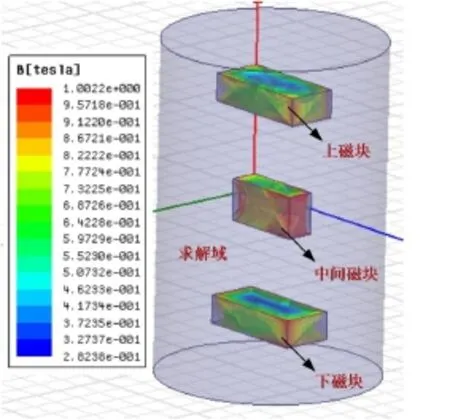
图12 三磁体有限元结构图

图13 三磁体型隔振器的力-位移曲线

图14 三磁体型隔振器的刚度-位移曲线

5 结语

通过矩形磁铁与机械弹簧并联设计了三磁体型准零刚度隔振器。

（1）利用基于磁极化强度与磁偶极子之间的关系，计算出单位长度两块磁体之间的静磁能，通过对静磁能求导得到两磁体间磁力。

（2）采用矩形磁铁作为负刚度元件，通过合理选择磁铁布置方式和充磁方向，可使其负刚度区间范围扩大，且在区间内刚度变化平缓。

（3）将磁铁尺寸参数作为对象，对充磁方向相同的上、中、下磁铁的刚度进行了优化，并通过有限元分析验证了解析模型的有效性。

（4）设计了三磁体型准零刚度隔振器，实现了高静低动的刚度特性，能有效解决低动刚度和失稳的矛盾，具有一定的工程应用价值。

[1]候九霄，朱海潮.双自由度自调吸振器及其吸振特性[J].噪声与振动控制，2015，35(6)：36-40.

[2]张晓平，何琳，周玮.一种新型磁致负刚度机构的研究[J].噪声与振动控制，2015，35(4)：159-162.

[3]ZHOU N,LIU K.A tunable high-static-low-dynamic stiffness vibration isolator[J].Journal of Sound and Vibration,2010,329:1254-1273.

[4]LI QIANG,ZHU YU,XU DENGFENG,et al.A negative stiffness vibration isolator using magnetic spring combined with rubber membrane[J].Journalof Mechanical Science and Technology,2013,27(3):813-824.

[5]ZHU TAO,BENJAMIN CAZZOLATO,ANTHONY ZANDER,et al.Vibration isolation using six degree-offreedom quasi-zero stiffnessmagneticlevitation[J].Journal of Sound and Vibration,2015,358:48-73.

[6]SHAN YUHU,WU WENJIANG,CHEN XUEDONG. Design of a miniaturized pneumatic vibration isolator with high-static-low-dynamic stiffness[J].Journal of Vibration andAcoustics,2015,137:1-8.

[7]ZHENG YISHENG,ZHANG XINONG,LUO YAJUN,et al.Design and experiment of a high-static-low-dynamic stiffness isolator using a negative stiffness magnetic spring [J].Journal of Sound and Vibration,2016,360:31-52.

[8]XU DAOLIN,YU QIPING,ZHOU JIAXI,et al. Theoreticaland experimentanalysesofa nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J].Journal of Sound and Vibration,2013, 332:3377-3389.

[9]WILL ROBERTSON,BEN CAZZOLATO,ANTHONY ZANDER.Theoretical analysis of a non-contact spring with inclined permanent magnets for load-independent resonance frequency[J].Journal of Sound and Vibration,2012,331:1331-1341.

[10]BISWAS B.A magnetic quadrupole from rectangular permanent magnets[J].Nuclear Instruments and Methods in Physics ResearchA,2009,605:233-242.

[11]WU WENJIANG,CHEN XUEDONG,SHAN YUHU. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness[J].Journal of Sound and Vibration,2014,333:2958-2970.

Magnetic Force Calculation of Rectangular Permanent Magnets and ItsApplication

CHAI Kai1,YANG Qing-chao2,ZHU Shi-jian2,LOU Jing-jun2
(1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China; 2.National Key Laboratory on Ship Vibration and Noise,Naval University of Engineering, Wuhan 430033,China)

Negative stiffness mechanism can be used to isolate low frequency vibration of systems.In this paper, analytical expressions of the magnetic force and stiffness of rectangular permanent magnets are derived by using the equivalent magnetic charge method.Meanwhile,the optimal arrangement and magnetization of the rectangular permanent magnets are obtained to accomplish the negative stiffness.Finally,the tri-magnet quasi-zero stiffness vibration isolation is designed.The simulation results show that the theoretical analysis is correct and the excellent low frequency vibration isolation performance is achieved without affecting the load ability.

vibration and wave;rectangular permanent magnets;negative stiffness;quasi-zero stiffness;low frequency vibration isolation

O328

：A

：10.3969/j.issn.1006-1335.2016.06.010

1006-1355(2016)06-0051-05+66

2016-07-11

国家自然科学基金资助项目(51579242)；国家自然科学基金青年科学基金资助项目(51509253)

柴凯(1989-)，男，湖南省益阳市人，博士研究生，研究方向为舰船动力装置振动噪声控制。

朱石坚(1955-)，男，湖南省双峰市人，教授，博士生导师。E-mail:hjcckll@sina.com