强振动环境下液压管道主动减振建模

潘文龙，张怀亮1,，彭 玲

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.中南大学 机电工程学院，长沙 410083）

强振动环境下液压管道主动减振建模

潘文龙2，张怀亮1,2，彭 玲2

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.中南大学 机电工程学院，长沙 410083）

针对在强振动环境下工作的液压管道，建立振动液压管道梁模型，并结合管道流固耦合横向振动模型建立管道的主动减振模型。运用特征线和差分计算方法求解该数学模型，并且研究主动振动相位差、频率、作用位置和幅值对管道振动的影响规律，得到各减振参数对管道最大幅值和最大应力的影响曲线。发现当振动相位差为π时能使管道的最大幅值和最大应力分别降低44.55%和39.69%，并且适当调整其他三个参数有更佳的减振效果。研究结果表明，使用主动减振方法能够有效减小管道的振动，为管道主动减振提供一定的理论参考。

振动与波；主动减振；特征线；流固耦合

液压管道在工作过程中由于外部支撑的振动与内部流体的流固耦合双重作用，会引起强烈振动，从而导致管内流体压力和流量的波动，波动的流体会对液压系统造成大的冲击，影响下游工作元件的正常工作，同时管道的剧烈振动会引起固定支撑的松动、管道的疲劳破坏等，严重时可能导致管道的变形破坏，引起事故，造成重大损失[1-2]。因此，研究液压管道的减振方法显得尤为重要。

目前就减振方法来说可以分为被动减振和主动减振。被动减振是利用隔振器件与被动式液压系统等被动阻尼元件或装置来消耗振动能量，达到振动抑制效果，装置结构一般比较简单，但有较大的局限性，减振系统参数无法跟随被控系统变化[3-4]。主动减振是近些年发展起来的，而且在土木工程、航空航天、机械工程、车辆运输等诸多领域获得了广泛的重视，它正好能够填充被动减振的空白，有较强的适应能力和发展空间。

主动减振通过向系统施加外力抵消系统中的振动，理论上可根据需要达到最佳的控制水平，其性能明显优于被动减振方法。

近年来，国内外有较多学者围绕主动减振问题进行了一些研究，Maillard Julien等人通过在管道外壁采用环状压电换能器做成的激振器来减小管内流体的振动[5]。Brennan M J设计非嵌入式激振器和传感器去主动控制管道流体的波动，实验表明该激振器能够有效抑制流体波动的传递[6]。焦宗夏等在液压能源管路系统振动主动控制的理论研究中提出对飞机液压能源管路系统进行消振的方法，采用压电陶瓷和参数寻优控制策略，通过理论分析和仿真验证该方法有良好的消振效果[7-9]。李广对风洞试验中悬臂的振动采用主动减振方法进行控制，并通过实验验证了该主动控制方法的有效性与可行性[10]。彭欢建立基础振动下液压管道流固耦合模型，并对模型进行数值求解和实验验证，证明了模型的正确性[11]。

现有主动减振的研究单独考虑减振参数对减振效果影响的文献并不多见，并且在研究主动减振的过程中都没有考虑基础振动对管道系统的影响。

针对横向基础振动对液压管道的影响，将液压管道简化为两端固支输流管道，对主动减振参数进行研究，以减小管道最大整体变形和应力为目标。

1 数学模型

与基础振动对管道应力的影响相比，流体脉动的作用要小得多，故不考虑流体脉动对管道应力的影响。为了减小管道的振动，在管道两个支撑之间外加一个振动作用于管道上，减小管道的振动。外加的振动即为主动减振，主动减振通过向系统施加外力抵消系统中的振动，理论上可根据需要达到最佳的控制水平。

彭欢建立了基础振动下管道流固耦合模型，通过改变管道的位移参数和边界条件加入了基础振动[11]。考虑主动减振下的基础振动和流固耦合模型，先建立基础振动下管道的主动减振连续振动梁模型，在此基础上再建立基础振动下流固耦合减振模型。

1.1 基础振动下管道主动减振连续振动梁模型的数学模型

液压管道是通过多个支撑件固定在主梁上的，主梁上的振动通过支撑件传递到液压管道上，以管道某一段两端固定支撑来说，可以将其看作一个连续振动的梁模型[12-13]。

图1所示为该连续振动模型的简化图，A-B为一段液压直管道，管道长为L。它在工作过程中会有强烈的振动，这个振动是通过支撑A、B传递给管道的，且假设支撑在外界横向激励作用下做简谐运动，基础振动的表达式为

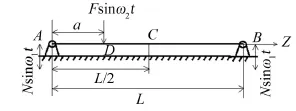
图1 基础振动下管道主动减振连续振动梁模型

其中N为横向基础振动幅值，ω1为基础振动频率。

为了减小管道的振动，在离A端距离为a的位置加主动减振振动，用以抵消管道中的振动，主动减振振动的表达式为

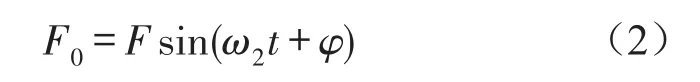
其中F为主动减振振动幅值，ω2为主动减振振动频率，φ为主动减振振动相位。

根据参考文献［12］中连续系统的振动，可得梁的弯曲振动微元的运动方程。

在图2（a）的坐标系中，此挠曲线为y=y(z,t)，为了得到梁振动的运动方程，在梁上截取长度为dx的一小段来分析，如图2（b），以此小段为脱离体，分别列出其在y方向及绕其左截面中点o′的平衡方程，有

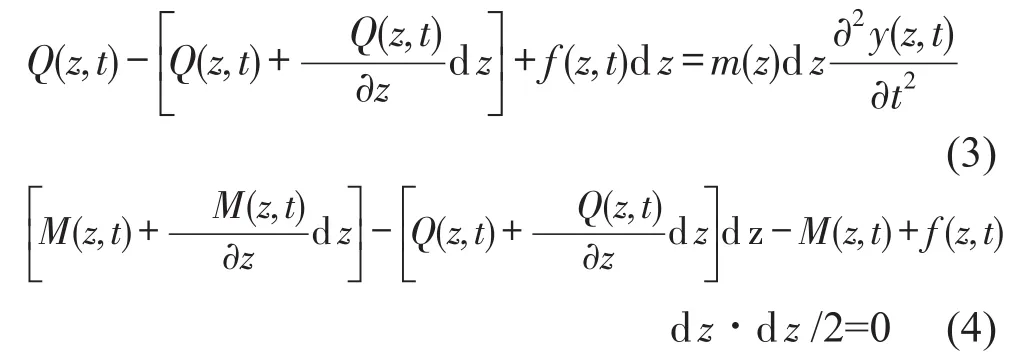
其中f(z,t)为作用在管道上的载荷密度，y(z,t)为管道位移与振动的挠曲线，M(z,t)为管道微元截面弯矩，Q(z,t)为管道微元截面剪力，m(z)为单位长度的管质量。

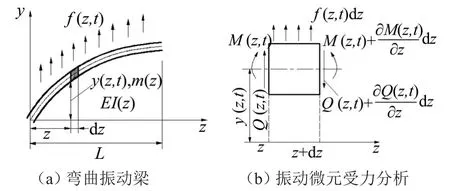
图2 梁的弯曲振动微元

1.2 基础振动下流固耦合减振模型

目前，描述输流管道系统流固耦合振动的数学模型有4-方程模型、8-方程模型、12-方程模型以及14-方程模型等，但应用最为广泛的就是4-方程模型[14-15]。

在轴向运动4-方程模型的建立过程中，分别以流体运动的连续方程、动量方程和管道的振动方程为基础，通过流体和固体结构在边界上的接触相容条件来实现两种介质之间的耦合。忽略管道的径向惯性作用力的影响，并且不考虑管道径向变形的情况，认为整个管道是处于同一水平面上，得到以下流固耦合经典4-方程数学模型。

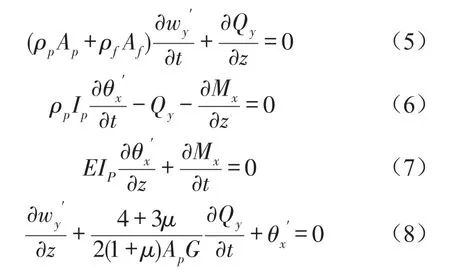
在流固耦合横向4-方程数学模型的基础上考虑基础振动Nsin(ω1t)和主动减振振动Fsin(ω2t+φ)的双重作用对管道系统的影响，需要对原有的横向4-方程模型稍作改动，在式（5）和式（8）中的横向运动位移项wy加入连续梁挠曲线y，即变换为变换为并在后续的分析过程中加入管道两端固定支撑和基础振动的边界条件，得到在任意t时刻任意z位置时管道的状态方程

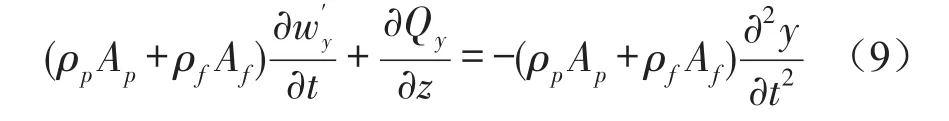
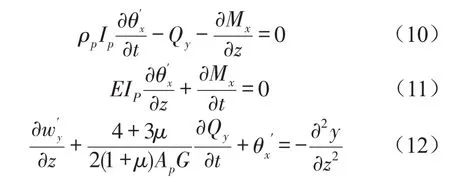
其中y=y(z,t)为基础振动下管道主动减振连续振动梁挠曲线方程，为连续梁挠曲线对时间t的二次求导为连续梁挠曲线对位置z的二次求导。

2 模型求解

2.1 梁的弯曲振动求解

根据式（3）和式（4）得到梁的弯曲振动的运动方程为

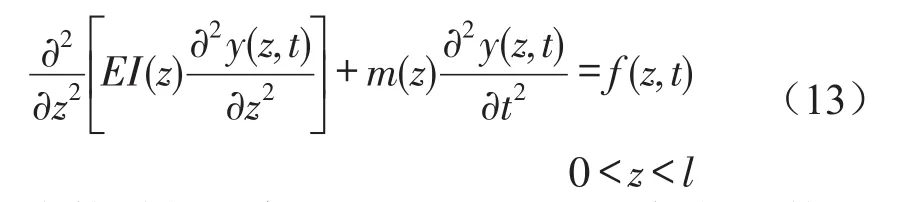
式中l为管道的长度，y(z,t)对于空间坐标的导数是4阶。

自由振动情况下f(z,t)=0，设同步运动为

2002年，我“鸟枪换炮”，用我3个月的工资1680元购买了一辆嘉陵弯杠摩托车。我驾驶着崭新的摩托车，戴上头盔，敞开外衣，加油提速，衣襟在身后飘舞，身上凉飕飕的，心里美滋滋的，那是一种骑士的洒脱。偶尔有辆小汽车绝尘而过，心里又有一种莫名的失落感。

其中Y(z)确定整条弦线在空间的形状，η(t)确定弦上各点的位移随时间的变化规律。

基础振动下两端固支梁的边界条件为

左端边界条件

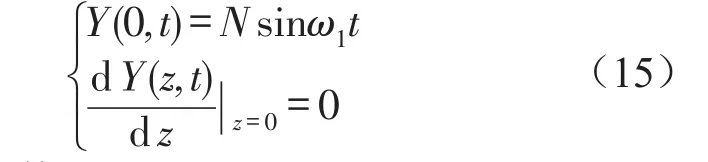
右端边界条件

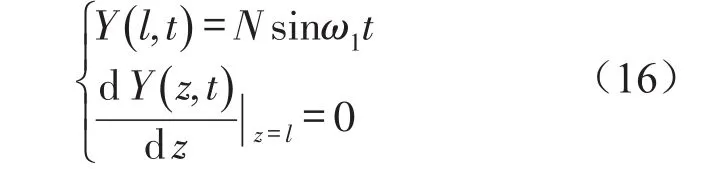
得到

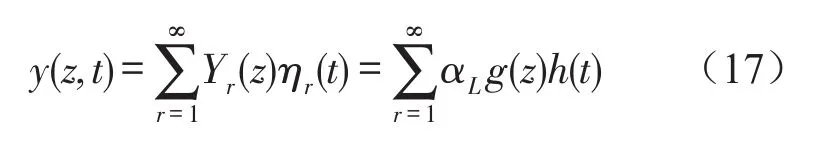
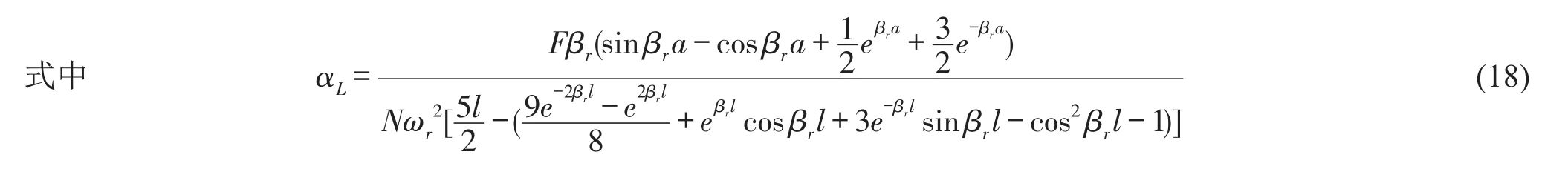
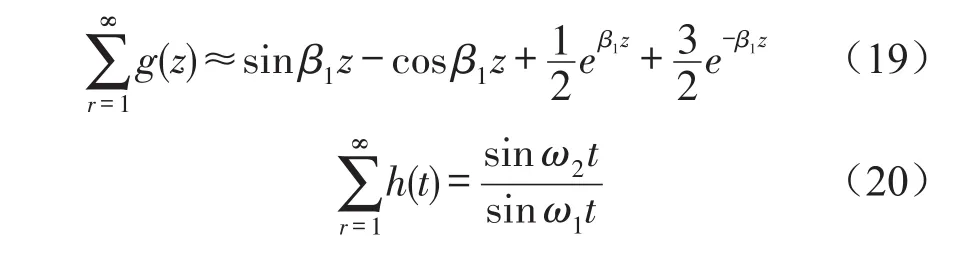
2.2 主动减振模型求解

对于式（9）-式（12）的求解方法目前已有几种方法可供选用，传递矩阵法和行波法已被广泛用于预测无摩擦系统和黏性阻尼系统的共振和振荡；特征线法以及特征线法和快速傅立叶变换相结合也已成功地用于频谱分析，有限元法以及特征线有限元法也得到广泛应用；此外，Laplace变换也常常应用于此类问题并已得到不错的发展[16-18]。

在时域分析中最为成功、使用最为广泛的方法之一是基于数值积分的特征线法。特征线是以偏微分方程的特征理论为基础，求解双曲型偏微分方程的一种近似计算方法，可以将偏微分方程转化为常微分方程，对于简单的问题可以得到解析解或近似解，复杂问题也可以得到准确度很高的数值解，而且它具有结构性强、程序编制容易实现等优点。在此，使用特征线法来求解方程。

为便于方程的求解，将式（9）-式（12）写成统一矩阵形式为

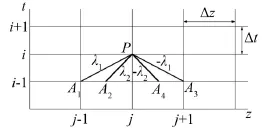
图3 特征线差分网格

图3即为有限差分网格图，特征线方程变成斜率为±λ1和±λ2的直线，将管道等分成N段，各段长度为Δz，时间步长取Δt，将平面t-z分成图3所示的矩形网格，将式（23）、式（25）代入式（24）并沿特征线积分以差分形式展开并整理得到

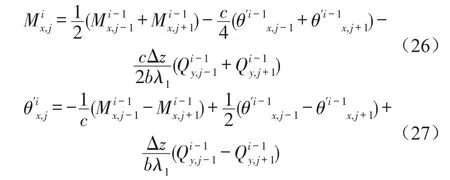
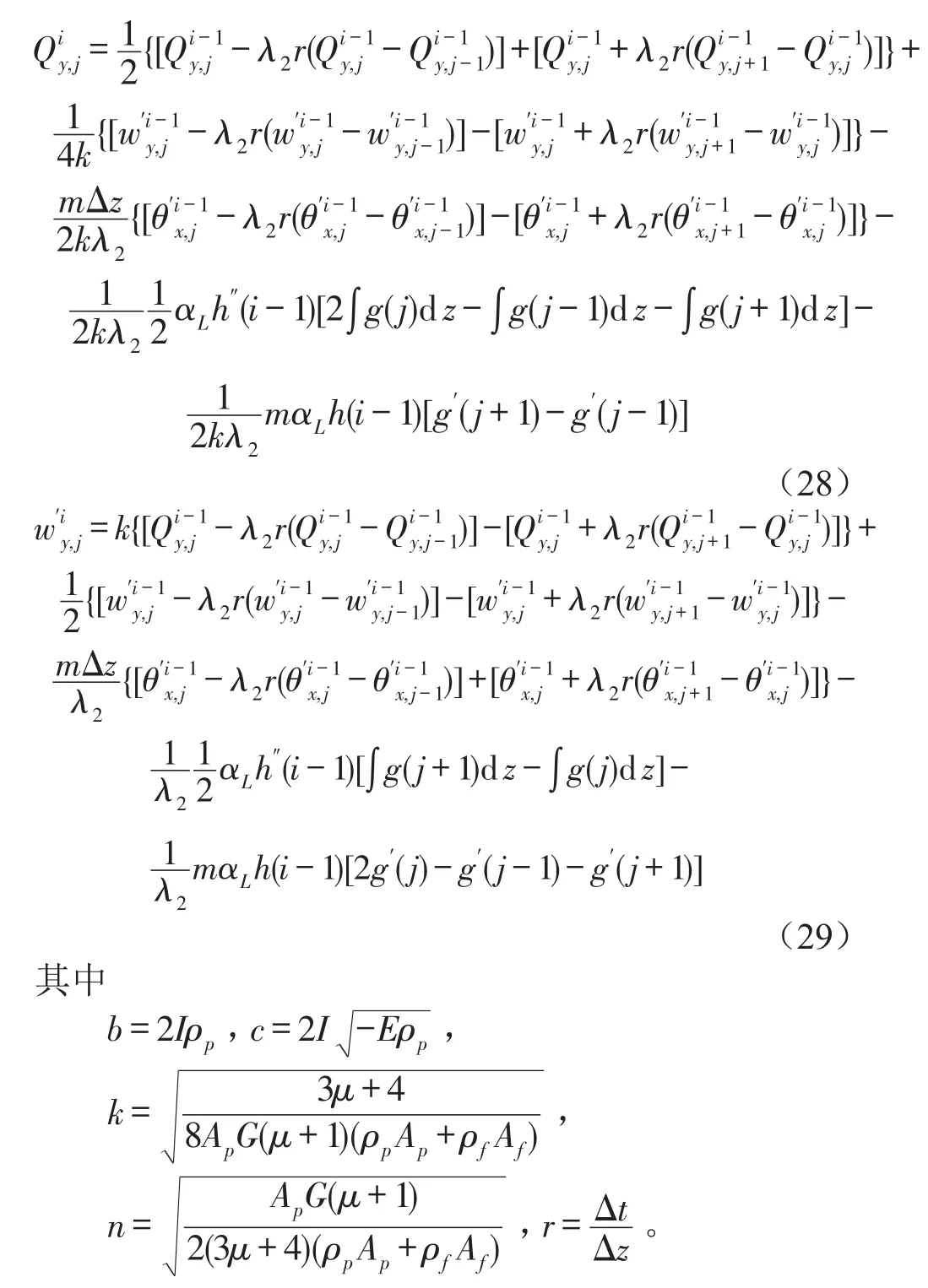
2.3 边界条件

2.3.1 进口边界条件

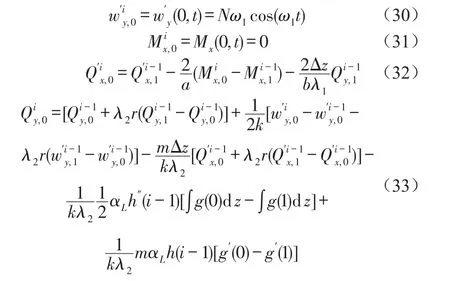
2.3.2 出口边界条件

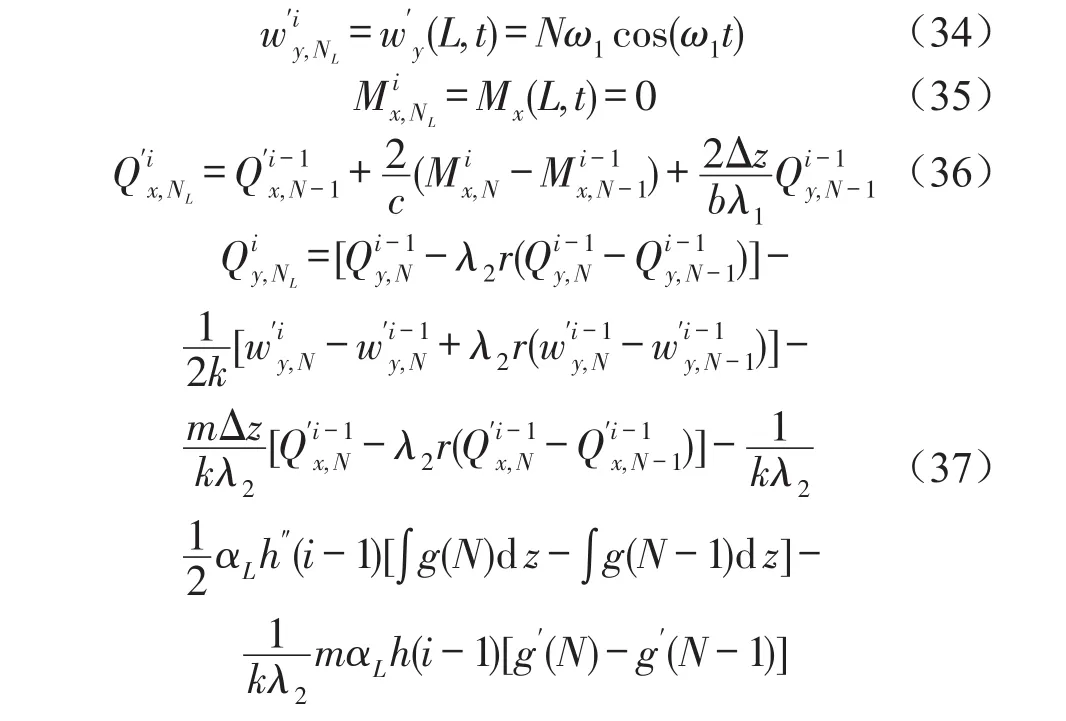
3 结果与分析

在固定支撑的管道两端施加频率为100 Hz、振幅为1 mm的基础振动，管内进口压力为10 MPa，出口液压油流速为5 m/s。分别研究主动减振振动频率、与基础振动相位差、幅值和作用位置对管道减振的影响。减振的目标值是管道总变形的最大值和最大应力，当这两个值都减小或者一个值减小另外一个值没有明显增大时，表明该主动减振振动能够起到减小管道振动的效果。

进行Matlab差分计算[19]，参数见表1。

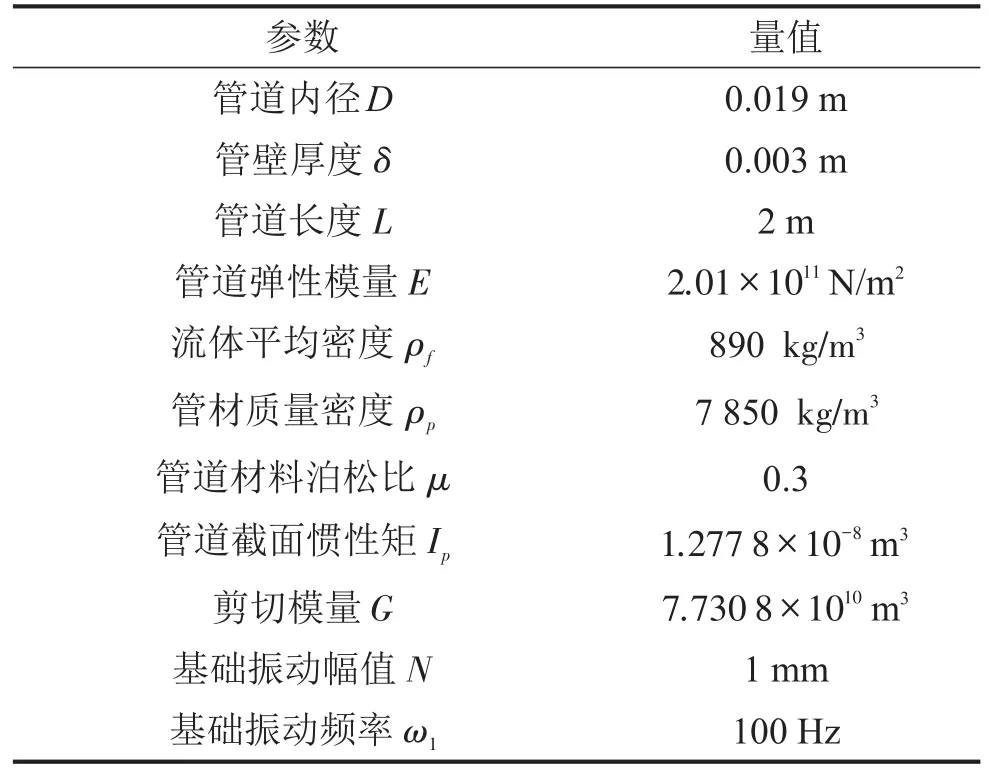
表1 液压管道工作参数

管道单元长度取Δz=2×10-4，积分时间步长取Δt=2×10-5。

在没有主动减振作用时，管道在基础振动作用下的最大总变形为1.851 8 mm，最大应力为129.56 MPa。

3.1 主动减振振动与基础振动相位角差值对管道振

动的影响

主动减振作用幅值为1 mm，频率为100 Hz，作用位置为管道中点。当相位差从0变到2π时，得到主动减振振动与基础振动相位角差值与管道总变形的最大值和最大应力的关系，见图4（a）、图4（b）。

由图4（a）、图4（b）可以看出，相位差与管道减振有密切的关系，当相位差为π时，主动振动与基础振动正好相反，有最佳的减振，最大变形为1.026 8 mm，最大应力为78.133 MPa，与无基础振动时的变形和应力相比较，最大变形减小了0.825 0 mm，达到44.55%；最大应力减小了 51.427 MPa，达到39.69%。说明适当调整主动减振振动与基础振动相位角差值可以起到较好的减振效果，并且当相位差为π时有最佳的减振效果。

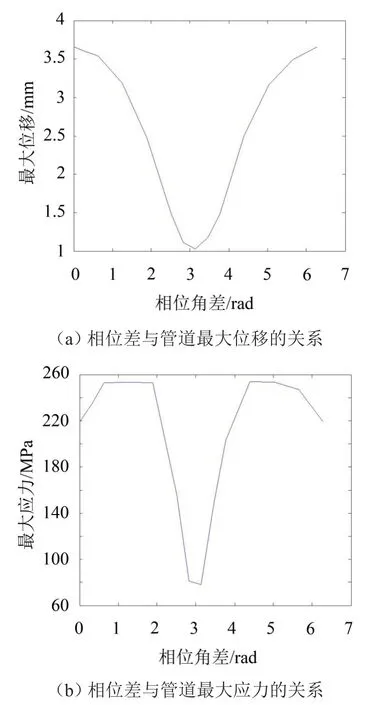
图4 相位差与管道最大位移和最大应力的关系

3.2 主动减振振动频率ω2对管道振动的影响

主动减振作用幅值为1 mm，相位差为π，作用位置为管道中点。当振动频率从10 Hz变到500 Hz时，得到ω2与管道总变形的最大值和最大应力的关系，如图5（a）、图5（b）所示。

由图5（a）、图5（b）可以看出，主动减振频率对管道减振效果有较大的影响，从整体来看，主动减振频率从10 Hz到500 Hz时，在100 Hz和240 Hz附近有相对较好的减振效果，这与管道系统的固有频率相关，当主动振动远离固有频率时减振效果更好。当主动减振频率为100 Hz时，有最佳减振效果，管道最大变形为1.026 8 mm，管道最大应力为78.133 MPa在选取主动减振频率时低频减振效果更加显著。

3.3 主动减振振动作用位置a对管道振动的影响

主动减振作用幅值为1 mm，频率为100 Hz，相位差为π，由于管道基础振动和形状是两端对称的，在考虑作用位置与减振的关系时只分析一半就可以了，当作用位置a从距离管道一端100 mm到1 000 mm时，得到a与管道总变形的最大值和最大应力的关系，如图6（a）、图6（b）所示。图中作用位置到管道一端的距离为a。

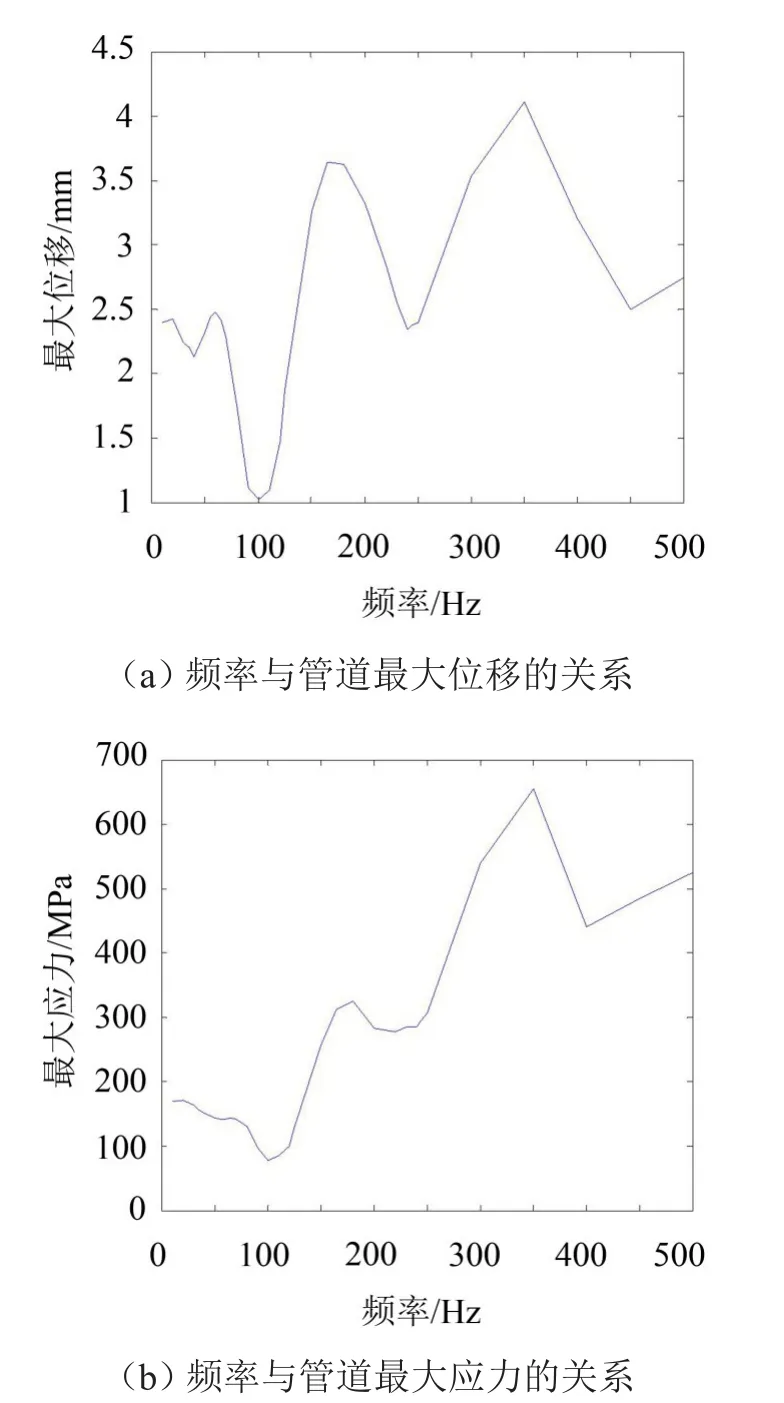
图5 频率与管道最大位移和最大应力的关系

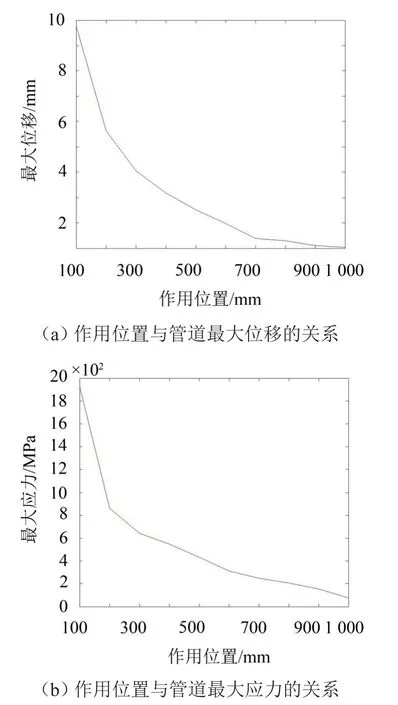
图6 作用位置与管道最大位移和最大应力的关系

由图6（a）、图6（b）可以看出，主动减振作用位置与管道减振效果有密切的关系，当作用位置越接近中间时减振效果越好，当a=1 000 mm时有最佳减振。因此，主动减振的作用位置应该尽量在管道中间。

3.4 主动减振振动幅值对管道振动的影响

主动减振频率为100 Hz，相位角差为π，作用位置为管道中点。当幅值从0.1 mm变到4 mm时，得到主动减振振动幅值与管道总变形的最大值和最大应力的关系，如图7（a）、图7（b）所示。

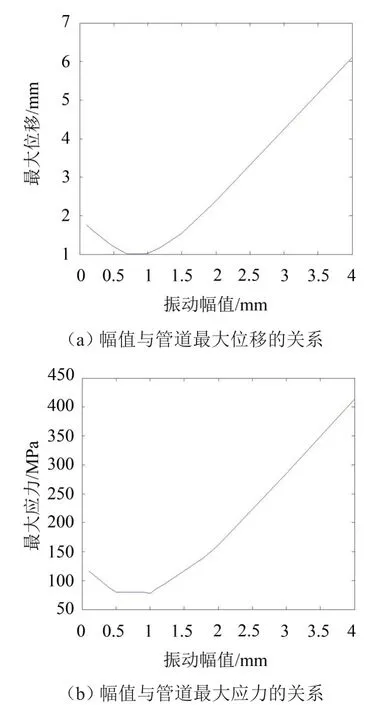
图7 幅值与管道最大位移和最大应力的关系

由图7（a）、图7（b）可以看出，当主动减振幅值在0.9 mm附近时，有最佳的减振效果，当幅值超过1.5 mm时管道的振动随幅值而线性增大。这是因为过大的主动减振在削弱管道本身振动后会进而增强管道的振动。主动减振的幅值应该与基础振动幅值接近。

综上所述，主动减振振动参数与管道的减振效果密切相关。因此，可以通过改变主动减振参数来减小管道的振动，适当调整各个参数可以得到良好的减振效果。

4 结语

（1）通过调整主动减振参数可以有效减小管道的振动，是一种有效的减振方法；

（2）当主动减振与管道振动相位差为π时有最佳的减振效果；

（3）低频的主动减振比高频的主动减振有更佳的减振效果；

（4）主动减振的作用位置应该尽量靠近管道中间。

[1]杨超.非横定充液管系统耦合振动特性及振动抑制[D].武汉：华中科技大学，2007.

[2]张立翔，黄文虎.输流管道流固耦合振动研究进展[J].水动力学研究与进展，2000，15(3)：366-379.

[3]胡宗武.机械结构振动主动控制发展综述[J].机械强度，1995，17（2）：55-60.

[4]王加春.机械振动主动控制技术的研究现状和发展综述[J].机械强度，2001，23(2)：156-160.

[5]MAILLARD JULIEN P,LAGO THOMAS L.Fluid wave actuator for the active control of hydraulic pulsations in piping systems[C].MAC-Proceedings of the 17 th International Modal Analysis Conference.1999.3727: 1806-1812.

[6]BRENNAN M J,ELLIOTT S J,PINNINGTON R J.A non-intrusive fluid-wave actuator and sensor pair for the active control of fluid-borne vibrations in a pipe[J].Smart Materials and Structures,1996.5:281-296.

[7]焦宗夏.基于旁路溢流原理的流体脉动主动控制[J].航空学报，2007，28(6)：1302-1306.

[8]焦宗夏.分布式液压流体脉动主动控制方法[J].北京航空航天大学学报，2007，33(9)：1060-1063.

[9]焦宗夏.液压流体脉动主动控制研究现状与展望[J].液压与机床，2006(9)：243-246.

[10]李广.基于模糊PID复合控制的振动主动控制研究[D].南京：南京航空航天大学，2008.

[11]彭欢.TBM液压直管道抗振结构策略研究[D].长沙：中南大学，2014.

[12]师汉民.机械振动系统（下册）第3版[M].武汉：华中科技大学出版社，2014：1-50.

[13]王蕴弢.基于Euler-Bernoulli梁模型输流管道流固耦合振动分析的快速算法[J].南京工业职业技术学院学报，2011，11(4)：14-17.

[14]WILKINSON D H.Acoustic,mechanical vibration in liquid-filled pipe work systems[C].Proceedings BNES International Conference on Vibration in Nuclear Plant. Keswick,May 1978,Paper 8.5:863-878.

[15]WIGGERT D C.Fluid transients in flexible piping systems(a perspective on recent developments)[C]. Proceedings of the 18 th IAHR Symposium on Hydraulic Machinery and Cavitation.Valencia,Spain,September 1996 58-67.

[16]曹亮.输流管道流固耦合振动特性分析[D].昆明：昆明理工大学，2004.

[17]吕海燕.输流管道流固耦合振动的频域分析[D].南京：河海大学，2006.

[18]朱建兵.轴向耦合水击振动方程的改进研究[D].昆明：昆明理工大学，2014.

[19]张志涌.精通Matlab R2012a[M].北京：北京航空航天大学出版社，2012：103-130.

Active Damping Modeling of Hydraulic Pipes under Strong Vibration Environment

PAN Wen-long2,ZHANG Huai-liang1,2,PENG Ling2
(1.State Key Laboratory of High Performance and Complex Manufacturing,Central South University, Changsha 410083,China; 2.College of Mechanical and Electrical Engineering,Central South University, Changsha 410083,China)

A beam model of vibrating hydraulic pipes is established for analyzing the vibration performance of the hydraulic pipes under strong vibration environments.Combining with the pipe’s fluid-structure coupling transverse vibration mode,the model for active vibration control of the pipes is established.Using characteristic line and the finite difference method,the mathematical model is solved.The influence of phase difference,frequency,location and amplitude of the active vibration on the vibration of the pipe is studied.The influence curves of the damping parameters on the pipe’s maximum amplitude and maximum stress are obtained.It is found that when the vibration phase difference isπ,the pipe’s maximum amplitude and maximum stress are reduced by 44.55%and 39.69%respectively.And the appropriate adjustments of the other three parameters can yield even better damping effects.This research indicates that using active damping method can effectively reduce the vibration of the pipes.It provides a theoretical reference for the pipe-active damping.

vibration and wave;active damping;characteristic line;fluid-structure coupling

TH113.1

：A

：10.3969/j.issn.1006-1335.2016.06.008

1006-1355(2016)06-0038-07

2016-06-23

国家重点基础研究发展计划资助项目(973计划，2013CB035400）

潘文龙（1992-），男，湖北省天门市人，硕士研究生，研究方向为液压元件动力学。

张怀亮，男，教授，博士生导师。E-mail:zhl2001@mail.csu.edu.cn