常用不规则聚集区探测方法*

中山大学公共卫生学院医学统计与流行病学系，卫生信息研究中心，广东省卫生信息学重点实验室（510080）

张王剑 杜志成 郭 貔 郝元涛△

常用不规则聚集区探测方法*

中山大学公共卫生学院医学统计与流行病学系，卫生信息研究中心，广东省卫生信息学重点实验室（510080）

张王剑 杜志成 郭 貔 郝元涛△

疾病的发生往往存在聚集性［1］。如何识别发病聚集区是公共卫生领域的一个关键问题。聚集区的识别，不仅为干预措施的分配提供依据，还可提供关于环境危险因素的信息，进而为发病机制的研究提供线索［2-3］。目前探测发病聚集区的方法有很多种，如Kulldorff空间扫描统计量方法［4-5］、局部空间相关性指数 （local index of spatial association，LISA）［6-7］、Turnbull方法［8-9］、Besag-Newell方法［10］等。其中，Kulldorff空间扫描统计量方法是应用最广泛的方法之一［11-13］，该方法所基于的假设是聚集区呈圆形［14］。这是一个非常苛刻的假设，在很多情况下并不成立。例如，某种疾病通过水源传播，则聚集区可能沿河道呈狭长分布［15］。

本文首先对经典的Kulldorff空间扫描统计量方法作简单介绍，然后通过文献综述的方式，归纳在该方法基础上发展而来的一系列常见的不规则聚集区探测方法。

Kulldorff空间扫描统计量方法

Kulldorff在 Naus［16］、Turnbull［9］等学者的工作基础上，于1997年提出了空间扫描统计量的概念［14］。该方法以研究区域内每个子区域的中心点代表该子区域。若扫描窗口覆盖某子区域的中心点，即认为该窗口包含该子区域（图1）。

首先，以某子区域A的中心点为圆心，画一个圆形扫描窗口，最初窗口内只包含子区域A，记为潜在聚集区｛A｝。然后，扫描窗口半径扩大，纳入一个新的中心点B，记为潜在聚集区｛A，B｝，依此类推，直到最大的扫描窗口所包含的人口数（或半径）达到预设的上限。对研究区域内所有的子区域，均执行如上过程。每一个圆形扫描窗内包含的区域都是一个潜在的聚集区。Kulldorff根据窗口内外发病风险比，构造了对数似然比（log likelihood ratio，LLR）统计量，作为筛选指标［14］。

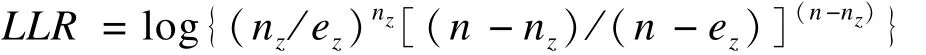
式中n为总病例数，为扫描窗口Z内的病例数，ez为窗口Z内的期望病例数，一般情况下中Pz和P分别为窗口Z内人口数和研究区域总人口数。为了克服多重检验问题［17］，Kulldorff采用蒙特卡洛（Monte Carlo，MC）方法对各潜在聚集区的LLR值进行假设检验［14，18］。LLR值最大的窗口称为“最有可能的聚集区（the most likely cluster，MLC）”，又称“一类聚集区”。其余的LLR值有统计学意义的窗口，称为“次级聚集区（secondary cluster）”，又称“二类聚集区”。Satscan软件可自动完成上述筛选过程［19］。

Kulldorff空间扫描统计量方法主要适用于潜在聚集区呈圆形或研究的空间单位为采样点的情况［14，20-22］。

图1 Kulldorff空间扫描统计量方法示意图

常用不规则聚集区探测方法

1.方法概述

在Kulldorff空间扫描统计量方法的基础上发展了一系列不规则聚集区探测方法。在研究区域内，任何具有连续性的子区域集合，都是潜在的聚集区。该定义将候选聚集区的形状从圆形拓展到了任意形状。但是，随着子区域数目的增大，候选聚集区的数目呈指数增长［23-24］。因此，如何精减候选聚集区的数目是不规则聚集区探测的核心问题。此外，所探测出的聚集区的实际意义，也是一个值得关注的问题。人们更倾向于获得并非过度不规则的、“紧缩型”的聚集区［25］。

2.贪心算法

贪心算法（greedy algorithm），又称“贪婪算法”，指某子区域A遵循“LLR最大化原则”向周围子区域“扩张”，每一次“扩张”只吸收能使LLR值上升最大的邻居，直到该区域的所有邻居均不能使LLR值继续增大，或聚集区长度（子区域数目）达到上限时，才停止搜索［15］。最后一步所得区域即为以A为中心的最佳候选聚集区。最小生成树算法（minimum spanning tree algorithm，MST）是一种重要的贪心算法，由Assuncao等［26］于2006年提出。该算法基于图论，将研究区域内的各个子区域以节点表示，子区域间的拓扑关系以节点间的连线（或称边）表示，同时赋予每条边一个权重，以度量子区域间发病率的差异。随机选取初始子区域，作为“叶”，根据权重最小化原则，逐步向相邻子区域“生长”，最后汇成树根（即所有子区域的集合）。从生成树中移除一条边，即可形成候选聚集区。该法的主要目的是筛选能够使LLR值最大化的边。

Patil和 Taillie［27］于2002年提出的 Upper level set统计量方法，是该类算法的特例。该类算法遵循权重最小化原则，产生的候选聚集区数目较少，运行速度非常快，但可能遗漏一些感兴趣的聚集区，在一定程度上存在功效低，或者过度估计［15，23，28-29］的问题。

Wieland等［29］在上述算法的基础上，于2007年提出了等密度欧氏最小生成树（density-equalizing euclidean minimum spanning tree，DEEMST）算法。与 Kulldorff空间扫描统计量方法相比，该方法的假阳性率较高，所识别出的聚集区往往较真实聚集区大，即存在“过度估计”问题。

贪心算法未能考虑到候选聚集区“扩张”过程中，相应的LLR值先降后升，甚至反弹到新高的情形。因此，该类算法存在“局部最大化问题（local maximum problem）”，不能得到整体最优解［15，30］。但是，贪心算法求解思路直观，速度快，且获得的结果往往是整体最优解较好的一个近似解，特别适用于研究范围内子区域数目较多的情形［31］。

3.惩罚算法

解决“过度估计”问题一个较好的办法是，对子区域的纳入标准实行“惩罚”，使得低风险子区域因为不满足“惩罚”后的纳入标准，而不能进入候选聚集区。惩罚算法主要包括几何惩罚算法和发病率临界惩罚算法。

（1）几何惩罚算法

几何惩罚算法，是一类对潜在聚集区的形状或搜索范围进行预先的限定，以压缩候选聚集区的数目，或防止识别出过度不规则的聚集区的算法。

①形状限定法

Kulldorff等［32］于2006年提出的椭圆形扫描窗口，即属于最直观的几何惩罚形式。为避免将潜在聚集区限定于某种特定的几何形状，Duczmal和Kulldorff等［33］于 2006年提出非压缩性惩罚（non-compactness penalty），将候选聚集区的面积与包绕该区的凸包面积之比作为惩罚系数的底，对LLR值实施惩罚。Yiannakoulias等［25］则根据潜在聚集区内边的数目构造“非连接性惩罚系数”的底。惩罚系数的指数α在0～1之间，值越接近1，惩罚效果越强。但是，α的设定比较主观。有些情况下，非连接性惩罚方法更加合理。当真实聚集区的形状的确呈过度不规则时，人为进行压缩未必合理［15，24］。

②扫描范围限定法

Tango等［28］于2005年提出了形状灵活的空间扫描统计量（flexibly shaped spatial scan statistic）。该算法将扫描范围限定在某子区域A及其K-1个最近邻之内。扫描范围内的K个子区域进行自由组合，形成长度为1～K的区域集合，其中具有连续性的区域，即为候选聚集区空间，而其中LLR最大者，即为一类聚集区。该算法继而被整合成软件FleXScan［34］，在国内外的疾病模式研究［35-37］和方法比较研究［38-39］中均有广泛应用。该方法有效避免了聚集区遗漏和过度估计的问题，也避免了贪心算法所存在的“局部最大化问题”。但是该算法在参数K的选择上缺乏客观标准。此外，该算法运算量大，适用于探测中小聚集区。

Yiannakoulias等［25］于 2007年提出了“深度限制（depth limit）”的方法，将贪心算法中每一步要求LLR值最大化，放宽到经过u步后，LLR值仍未达到新高，聚集区才停止“扩张”，从而缓解了“局部最大化”问题。

几何惩罚算法适用于研究者具备关于真实聚集区的大小、形状等属性的先验知识，并能够根据先验知识预设惩罚参数的情形。但是，预设参数的难度大，主观性强，尤其对聚集区形状的限定往往缺乏说服力。

（2）发病率临界惩罚算法

为了解决过度估计问题，Tango和 Takahashi［40］以对每一个子区域的发病人数的异常程度设定下限的办法，对LLR值进行如下惩罚：

上述惩罚方法与灵活扫描统计量方法［28］联合应用，既解决了以往扫描方法“过度估计”的问题，又冲破了灵活扫描统计量方法中对K大小的限制。但是，子区域发病人数异常程度的下限须事先设定。Tango建议以0.20作为al的默认值［41］。

4.迭代算法

（1）模拟退火算法

Duczmal和 Assuncao［30］于 2004年提出了一种图论方法-模拟退火算法（simulated annealing algorithm，SA），又称“伪最优方案”［24］。该算法首先运用 Kulldorff空间扫描统计量方法，筛选出一类聚集区，然后通过增减子区域，来寻找使LLR最大的不规则聚集区。如果新候选聚集区相对于上一步聚集区，LLR值增长不大或无增长时，则从新候选聚集区中随机选择一个作为下一步筛选的基础［24］。这种随机选择的方法，降低了“局部最大化”风险。但是，SA算法非常复杂，其中所设的参数难以解释，且缺乏设定标准［26］。Tango等［28］利用Duczmal教授提供的程序进行模拟，发现在大部分情形下，该算法所识别出的区域远大于真实聚集区。

Zhijun Yao等［23］吸收了现有不规则扫描方法“相邻扩张”的思想，于2011年提出了两种基于迭代的算法--最大似然优先算法（maxima-likelihood-first，MLF）和非贪心增长算法（non-greedy growth，NGG）。

（2）MLF算法

该算法首先计算所有子区域的LLR值，并以其中最大者作为初始区域，与其邻居组成新区域。从初始区域和新区域中选出LLR值最大者作为新的初始区域。重复以上过程，直到选出的区域覆盖一半区域或一半人口。

相对于最小生成树算法，MLF算法每次“扩张”基于多个“种子”，在一定程度上减弱了前者“方向性”生长的问题（即“局部最大化问题”）。该算法运行速度较快，但是迭代过程默认将聚集区锁定在初始区域周围。该法主要适用于扫描区域内子区域数目较少，且不存在多个发病率过高的子区域的情形。

（3）NGG算法

在“相邻扩张”中，候选聚集区数目主要取决于上一步的区域数（即“基数”）和各区域的邻居数。扩张过程中，基数呈指数增长，但各区域的邻居数变化不大。因此，控制候选聚集区数目的最好办法是限定基数。

首先设定基数上限M，将所有子区域放进临时列表，并计算每个区域的LLR，及它们的平均邻居数L；从临时列表中，按LLR值筛选出N＝M／L个区域（设为集合A）；清空列表，并将集合A及它的邻居所组成的新候选聚集区放入临时列表里。重复以上过程，直到选出的区域覆盖一半区域或一半人口。

迭代算法，区别于贪心算法之处在于每一次迭代中，新候选聚集区的构建基于多个种子。但是，种子仍然是按一定标准（如在候选列表中LLR排前几的区域）筛选出来的，未必是所有候选种子的随机样本。未来的研究仍然可以从该方面着手，进一步提高迭代算法的性能。

除了以上扫描方法之外，聚集区探测的思想还可根据具体研究问题的背景，与遗传算法［42-44］、决策树算法［45］、基于格点化的方法［46-47］等相结合，充分发挥各种算法的优势，解决具体问题。随着建模理论和技术的发展，通过建模方法，拟合发病与危险因素之间的关系，并估计各区域发病的相对危险度，直观呈现各区域发病风险的高低，逐渐成为研究热点和主要趋势［48-50］。

问题和展望

不规则聚集区探测方法的提出，克服了传统的圆形窗口扫描的局限性，极大地提高了高发区域识别的准确性。不同探测方法的适用情形不同。在某些空间模式下，某种探测方法可能表现出明显的优势，但很难保证该方法在所有情形下，均具有相对优势［50］。各种方法提出时，须通过模拟研究进行性能评估。已有研究在设定空间模式时，存在两个问题：一是所设聚集区形状过少，常常为圆形、环形等规则形状；二是发病率或相对危险度的水平数过少，往往假定聚集区内外共两水平，因此只能局限于对一类聚集区识别能力的评估上［25］。此外，已有研究发现，以LLR值作为筛选指标存在“过度估计”的问题［26，28］。未来的研究，需要寻找更加准确的LLR值惩罚方法，并设置全面的空间模式，对这些方法的性能进行模拟评估。

［1］Tobler WR.A Computer Movie Simulating Urban Growth in the Detroit Region.1970：234-240.

［2］Wheeler DC.A comparison of spatial clustering and cluster detection techniques for childhood leukemia incidence in Ohio，1996-2003.Int JHealth Geogr，2007，6：13.

［3］Jennings JM，Curriero FC，Celentano D，et al.Geographic identification of high gonorrhea transmission areas in Baltimore，Maryland.Am JEpidemiol，2005，161（1）：73-80.

［4］董选军，滕世助，余运贤，等.扫描统计量在流行性腮腺炎聚集性判断的应用.中国卫生统计，2014（05）：863-864.

［5］康万里，郑素华.空间扫描统计在中国菌阳结核病分布中的应用.中国卫生统计，2012（04）：487-489.

［6］何明祯，刘剑，依火伍力，等.高山地区钉螺分布的空间特征研究.中华流行病学杂志，2011，32（4）：361-365.

［7］徐珏，黄春萍，宋姝娟，等.Moran’s I系数分析手足口病的空间自相关性.浙江预防医学，2014（6）：541-543，556.

［8］裴姣，殷菲，李晓松，等.Turnbull方法在四川省结核病空间聚集性分析中的应用初探.中华疾病控制杂志，2011，15（5）：441-444.

［9］Turnbull BW，Iwano EJ，Burnett WS，et al.Monitoring for clusters of disease：application to leukemia incidence in upstate New York..A-merican journal of epidemiology，1990，132（1 Suppl）：S136-S143.

［10］冯海欢，殷菲，李晓松，等.Besag_Newell方法在内蒙古布鲁氏菌病空间聚集性分析的应用初探.中华疾病控制杂志，2011，15（6）：527-530.

［11］赵飞，朱蓉，张利娟，等.SaTScan在湖沼型血吸虫病聚集区域探测中的应用.中国血吸虫病防治杂志，2011，23（1）：28-31.

［12］李秀央，陈坤.扫描统计量的理论及其在空间流行病学中的应用.中华流行病学杂志，2008，29（8）：828-831.

［13］Deng T，Huang Y，Yu S，et al.Spatial-temporal clusters and risk factors of hand，foot，and mouth disease at the district level in Guangdong Province，China.PLoS One，2013，8（2）：e56943.

［14］Kulldorff M.A spatial scan statistic.Communications in Statistics-Theory and methods，1997，26（6）：1481-1496.

［15］Yiannakoulias N，Wilson S，Kariuki HC，et al.Locating irregularly shaped clusters of infection intensity.Geospat Health，2010，4（2）：191-200.

［16］Naus JI.The Distribution of the Size of the Maximum Cluster of Points on a Line.1965：60，532-538.

［17］殷菲.时-空扫描统计量在传染病早期预警中的应用研究.四川大学流行病与卫生统计学，2007.

［18］Dwass M.Modified Randomization Tests for Nonparametric Hypotheses.1957：28，181-187.

［19］Kulldorff M.Satscan User Guide v7.0.

［20］钱莎莎，郭巍，王丽艳，等.基于地理信息系统的我国艾滋病聚集性流行的空间分析.中国卫生统计，2014（06）：1064-1067.

［21］唐咸艳，周红霞.扫描统计及其在流行病学中的应用.中国卫生统计，2011（03）：332-337.

［22］袁东方，应莉娅，刘志芳，等.基于谷歌地图的传染病空间聚集性分析.中国卫生统计，2014（03）：414-417.

［23］Yao Z，Tang J，Zhan FB.Detection of arbitrarily-shaped clusters using a neighbor-expanding approach：A case study on murine typhus in South Texas.International Journal Of Health Geographics，2011，10（23）.

［24］Duczmal L，Duarte AR，Tavares R.Extensions of the scan statistic for the detection and inference of spatial clusters.2009.

［25］Yiannakoulias N，Rosychuk RJ，Hodgson J.Adaptations for finding irregularly shaped disease clusters.INTERNATIONAL JOURNAL OF HEALTH GEOGRAPHICS，2007，6（28）.

［26］Assuncao R，Costa M，Tavares A，et al.Fast detection of arbitrarily shaped disease clusters.Stat Med，2006，25（5）：723-742.

［27］Patil GP，Taillie C.upper level set scan statistic for detacting arbitrarily shaped hotspots.2004：11，183-197.

［28］Tango T，Takahashi K.A flexibly shaped spatial scan statistic for detecting clusters.Int JHealth Geogr，2005，4：11.

［29］Wieland SC，Brownstein JS，Berger B，et al.Density-equalizing Euclidean minimum spanning trees for the detection of all disease cluster shapes.Proc Natl Acad Sci USA，2007，104（22）：9404-9409.

［30］Duczmal L，Assunɕão R.A simulated annealing strategy for the detection of arbitrarily shaped spatial clusters，2004，2：269-286.

［31］刘桂林.基于贪心算法的时间片优先级排课算法的研究与应用.湖南大学计算机技术，2013.

［32］Kulldorff M，Huang L，Pickle L，et al.An elliptic spatial scan statistic.Stat Med，2006，25（22）：3929-3943.

［33］Duczmal L，Kulldorff M，Huang L.Evaluation of spatial scan statistics for irregularly shaped clusters.JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS，2006，15（2）：428-442.

［34］ Takahashi K，Yokoyama T，Tango T.FleXScan：Software for the flexible spatial scan statistic.2004.

［35］Demoury C，Goujon-Bellec S，Guyot-Goubin A，et al.Spatial variations of childhood acute leukaemia in France，1990-2006：global spatial heterogeneity and cluster detection at'living-zone'level.EUROPEAN JOURNAL OF CANCER PREVENTION，2012，21（4）：367-374.

［36］周剑南，冯子健，谭柯，等.Flexible空间扫描统计量在传染病聚集性探测的应用研究.中华疾病控制杂志，2010（06）：475-478.

［37］张文增，李长青，冀国强，等.空间扫描统计量在手足口病空间聚集性研究中的应用.中国卫生统计，2012（04）：507-509.

［38］You W，Tao P，Chenghu Z，et al.ACOMCD：a multiple cluster detection algorithm based on the spatial scan statistic and ant colony optimization.Computational Statistics＆Data Analysis，2012，56（2）：283-296.

［39］Ramis R，Gomez-Barroso D，Lopez-Abente G.Cluster detection of diseases in heterogeneous populations：an alternative to scan methods.GEOSPATIAL HEALTH，2014，8（2）：517-526.

［40］Tango T，Takahashi K.A flexible spatial scan statistic with a restricted likelihood ratio for detecting disease clusters.STATISTICS IN MEDICINE，2012，31（30SI）：4207-4218.

［41］Tango T.A spatial scan statistic with a restricted likelihood ratio.200875-95.

［42］Duczmal L，Cancado ALF，Takahashi RHC，et al.A genetic algorithm for irregularly shaped spatial scan statistics.COMPUTATIONAL STATISTICS＆DATA ANALYSIS，2007，52（1）：43-52.

［43］Sahajpal R，Ramaraju GV，Bhatt V.Applying niching genetic algorithms for multiple cluster discovery in spatial analysis.Proceedings of International Conference on Intelligent Sensing and Information Processing，2004：35-40.

［44］Cancado A L F，Duarte A R，Duczmal L H，et al.Penalized likelihood and multi-objective spatial scans for the detection and inference of irregular clusters.International Journal of Health geographics，2010，9（55）.

［45］Gaudart J，Poudiougou B，Ranque S，et al.Oblique decision trees for spatial pattern detection：optimal algorithm and application to malaria risk.BMC Med Res Methodol，2005，5：22.

［46］Yiannakoulias N，AK，Schopflocher D，et al.Using Quad Trees to Generate Grid Points for Applications in Geographic Disease Surveillance.2007：3，1-9.

［47］Boscoe FP，McLaughlin C，Schymura MJ，et al.Visualization of the spatial scan statistic using nested circles.HEALTH＆PLACE，2003，9（3）：273-277.

［48］张王剑，季振东，郭貔，等.广东省2009-2012年手足口病流行趋势分析.中山大学学报（医学科学版），2014，35（4）：607-613.

［49］Aamodt G，Samuelsen SO，Skrondal A.A simulation study of three methods for detecting disease clusters.Int J Health Geogr，2006，5：15.

［50］Meliker JR，Sloan CD.Spatio-temporal epidemiology：principles and opportunities.Spat Spatiotemporal Epidemiol，2011，2（1）：1-9.

国家自然科学基金面上项目（81473064）

△通信作者：郝元涛，E-mail：haoyt＠mail.sysu.edu.cn

郭海强）