统计推断与平均组间效应*

第四军医大学口腔医院信息科

蔡宏伟

·学术讨论·

统计推断与平均组间效应*

第四军医大学口腔医院信息科

蔡宏伟

统计学的主要目的之一是借助已经发生的事件对未来事件发生的可能性做出统计推断［1］。现代统计学理论框架的产生和发展与随机化方法的应用推广密不可分［2-3］，随机对照临床试验是公认的评价临床干预措施的金标准，随着信息技术在医疗领域的应用，电子数据越来越多，观察性数据的获取成本不断降低，由观察性研究数据做出统计推断越来越受到重视［4］。观察性研究的基本思路是尽量模拟随机化研究的特性，通过“匹配”或“调整协变量”等统计学方法对混杂因素进行“均衡”。我们在统计推断中使用“研究群体”的平均组间效应（average treatment effect，ATE）推断“目标个体（或群体）”的ATE。不论是随机对照临床试验还是观察性研究，试验人群、调整后人群与拟推断目标人群的“同质性”都是一个需要考虑的重要问题［5］。如果没有遵循正确的基本“原则”，就很有可能得出错误的结论。

统计推断中的根本问题

假设一个个体u，有两种治疗方式可供选择，T＝｛1，0｝。当 t＝1时，个体接受治疗干预；当 t＝0时，个体接受对照干预。Y1（u）表示个体u接受治疗干预的效应，Y0（u）表示个体u在同一时间接受对照干预的效应。则对于每一个受试个体u，治疗干预相对于对照干预的治疗效应差异

因为个体u不可能在同一时间既接受治疗干预，又接受对照干预，这就导致个体u在某个特定时间段的治疗效应与对照效应的差值（即个体治疗干预与对照干预的对比）无法直接求出。这就是Rubin提到的统计推断中的基本问题［6］，几乎所有的统计推断工作都围绕如何解决这一问题展开。

我们很容易想到，需要找到一个与个体u类似的人群，用U表示，也就是我们需要做出统计推断的目标人群，用PATE来代表目标人群的平均组间效应。而我们推断PATE时候，总是需要一个试验样本的，即我们只能根据一个试验样本求出SATE。当这个试验样本是从总体人群中随机抽样得到时，SATE＝PATE。虽然实际上，我们可能永远也无法证明这一点［1］。

表1 分两组情况下，个体u治疗组效应和对照组效应的可观测值和反事实值

在将样本受试者分为两组的情况下，如表1所示，这4种效应中，只有效应A和效应D是可以观测到的。效应B和效应C理论上存在，但是实际上观察不到，也被称作反事实。

样本平均组间效应SATE，是试验样本中所有受试者的治疗组与对照组的平均组间效应差值，如公式2所示，

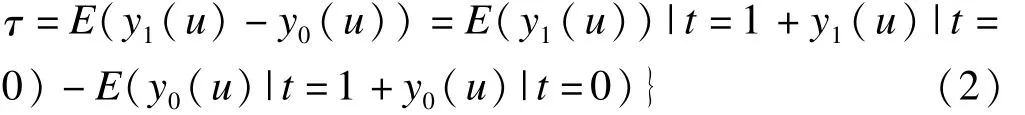
于是所有统计学的推断问题集中到两点：

（1）如何利用实际可测的数据替换公式（2）中的反事实数据，求出τ，即SATE。

（2）由SATE推断PATE时，试验人群与目标人群是否具有同质性。

随机化研究的平均组间效应

随机对照临床试验被称作评价治疗干预措施的金标准，而随机化原则是这一金标准的核心和基础［3，7］。随机化有2个特性，即不可预测和机会均等，不可预测可以避免选择偏倚，机会均等可以使组间均衡可比。在随机化均衡组间基线水平的基础上，对不同的组分别实施不同的干预，就可以推断出不同干预的效果差别。

在随机分组的情况下，治疗组与对照组的基线水平在理论上完全一致，所以可以分别用治疗组的治疗效应A代替总人群的治疗效应（A+C），用对照组的对照效应D代替总人群的对照效应（B+D），此时，有

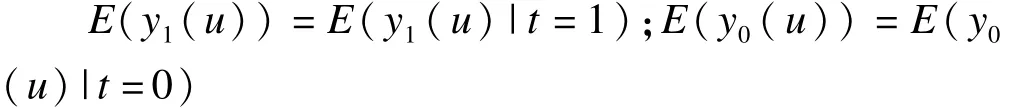
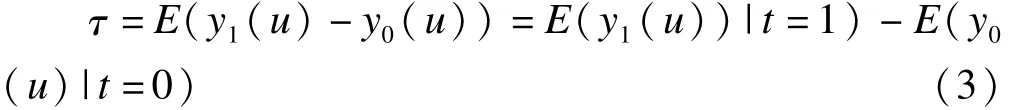
治疗组的治疗效应 E（y1（u）｜t＝1）和对照组的对照效应 E（y0（u）｜t＝0）都是可测的，所以 SATE是可以直接求出的。此时治疗组与对照组的平均组间效应ATE也就是组间的边际治疗效应（marginal treatment effect，MTE）［8］。

在我们需要均衡的因素中，可以分为已知的可以观测到的混杂因素和未知的无法观测到的混杂因素。而实际上，我们无法评判随机化是否对所有的已知和未知因素都均衡得很好［1］。在小样本情况下，简单随机化并不能够严格做到组间的“均衡可比”，比如将20个受试者分到两组，则两组受试例数比值差别大于12：8的可能性为0.19。当需要均衡的因素很多时，如，有6个影响因素，每个因素有3个水平，则共有36个＝729个水平，如果每个水平上的病例数不是足够多，那么即使用分层区组随机化也无法保证在所有水平上各组间都均衡可比［9-10］。由此，我们希望首先控制好那些通过实践已经被证明的重要的混杂因素。因此，动态随机化方法（最著名的如最小化法）因为能在相同的情况下，均衡更多的混杂因素，所以在现代临床试验中得到越来越广泛的应用［9，11-12］。

通过随机化的结果进行统计推断，关键还要看上文所指出的第2个问题，即试验人群与目标人群的同质性。以新药临床试验（要求最严格的临床研究）中的随机对照临床研究为例，受试个体一般需要经过“纳入／排除”标准的筛选。比如；排除掉怀孕妇女、儿童以及危重患者。此外，由于人种基因型、生活习俗以及自然环境等的差异，由北美或欧洲人群得出的SATE与我国人群中的SATE很可能是不一致的。因此，将“试验人群”得到的SATE推论到“目标人群”受到限制，这也是我们国内医院的临床科室不能直接使用国外的临床指南，而需要在其基础上做出调整的根本原因。

观察性研究的平均组间效应

在观察性研究中，由于没有“纳入／排除”标准等限制，因此其人群更接近“真实世界”的目标人群。但是通过观察性研究得到的数据可能有偏倚或混杂因素的影响，我们在分析时一般需要进行“匹配”或者“协变量调整”［13］。各种不同的调整方法，实际是通过排除掉一些“因差异较大无法匹配”的受试个体或者虚拟出“假定的标准人群”，然后进行统计推断。

以目前比较流行的非随机数据研究方法倾向评分匹配（propensity score matching，PSM）为例［14］，在计算倾向评分的过程中，倾向评分的值会因纳入模型协变量的不同而有所变化。在实际中，只能纳入“已知的”并且是“被观测到的”协变量，而未知协变量在组间的分布情况是未知的。也就是说，虽然PSM方法做了类似“事后随机化”的处理，均衡了组间已知的混杂因素，但是对于未知的协变量对研究结果的影响仍然是无能为力的［15］。对于上文中提到的第一个关键问题，在观察性研究中，利用实际可测的数据替换公式（2）中的反事实情况时，可能因未知因素的影响，得到的τ与实际的τ不同。

在某些情况下，SATE的子集SATT（sample average treatment effect for the treated）更受到关注。如患肺癌的病人根据是否使用某种较昂贵的抗癌药物被分为2组，选择使用该抗肺癌药物的治疗组病人与不使用该抗癌药物的对照组病人在构成上可能不同（如经济条件不同）。此时，我们更关注的是接受抗癌药物治疗的病人群体的平均组间效应SATT，可以用公式（4）表示。假设治疗组个体数量远小于对照组个体数量，就可以通过以治疗组个体为基准，通过匹配构建用于估计“治疗组病人”组间效应的试验虚拟人群。如公式4所示，E（y1（u）｜t＝1）是实际可测的，E（y0（u）｜t＝1）是通过匹配得到的。

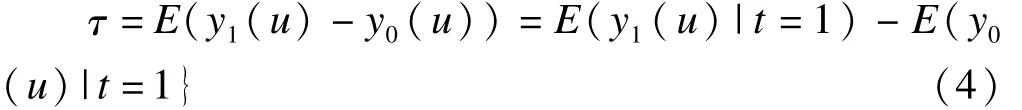
而且，如果在 PSM中使用“卡钳匹配法”［16-17］，则匹配后得到的“虚拟人群样本”排除了治疗组和对照组中PS值不能重叠匹配的个体，因此匹配后得到的“虚拟人群样本”的 NSATE（new sample average treatment effect）可能与原始人群的SATE不同。使用其它的方法如分层调整、模型调整或者加权法调整等与匹配法调整的情况类似［18-19］。不论使用哪种方法，“样本试验人群”的构成已经发生变化。因此由观察性研究得出的结论，在推广到其他人群时，除了关注组间的已知的混杂因素外，还需要对试验样本的人群及调整后人群的基本特征做出说明，以方便读者自己判断试验得出的结论对自己实践的指导意义。

小 结

在需要做出统计推断时，随机化研究对比观察性研究的优势在于：随机化研究可以同时均衡样本组间的“已知混杂因素”和“未知混杂因素”，而观察性研究最多可以通过统计模型在事后均衡“已知混杂因素”，而对“未知混杂因素”则无能为力。因此，随机化研究可以较准确得出SATE（样本平均组间效应）；而观察性研究因纳入的混杂因素不全，使得到的SATE可能与实际的SATE有一定的差异。但这种差异会随着在模型中纳入更准确的混杂因素而逐渐减小。

在由SATE做出推断的过程中，随机化研究与观察性研究都各有短板。随机化研究因为经过纳入排除标准的筛选，而与总体发病人群存在差异。而观察性研究在调整混杂因素的同时，原有人群中的构成发生了变化。对于观察性研究，由于需要对混杂因素进行调整，而所有的调整（包括随机化方法中的限制性随机化模型）都建立在模型的基础上，如果模型正确，则混杂因素效应减少；如果模型不能反映实际情况，则混杂效应仍会存留，所得的SATE与实际的SATE存在差异。而且，试验组和对照组的混杂因素是否全部被纳入模型，我们永远也无法确认。

人体本身很复杂，与外界环境等因素相互作用就更复杂。在临床研究中，有我们认识到的因素，还有很多我们尚未认识到的因素。在由试验样本对目标人群做出推断时，除了需要考虑有无混杂因素的影响，还需要考虑试验样本与目标个体或人群是否具有同质性。

［1］Holland PW.Statistics and Causal Inference.Journal of the American Statistical Association，1986，81（396）：945-960.

［2］Jacquez JA，Jacquez GM.Fisher's randomization test and Darwin's data--a foot note to the history of statistics.Math Biosci，2002，180：23-28.

［3］Hall NS..Fisher and his advocacy of randomization.J Hist Biol，2007，40（2）：295-325.

［4］Anglemyer A，Horvath HT，Bero L.Healthcare outcomes assessed with observational study designs compared with those assessed in randomized trials.Cochrane Database Syst Rev，2014，4：R34.

［5］Marcus SM，Stuart EA，Wang P，et al.Estimating the causal effect of randomization versus treatment preference in a doubly randomized preference trial.Psychol Methods，2012，17（2）：244-254.

［6］Rubin DB.Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies.Journal of Educational Psychology，1974，66（5）：688-701.

［7］Greenland S.Randomization，statistics，and causal inference.Epidemiology，1990，1（6）：421-429.

［8］Austin PC.The performance of different propensity score methods for estimating marginal hazard ratios.Stat Med，2013，32（16）：2837-2849.

［9］Pocock SJ，Simon R.Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trial.Biometrics，1975，31（1）：103-115.

［10］Lachin JM.Statistical properties of randomization in clinical trials.Control Clin Trials，1988，9（4）：289-311.

［11］Cai HW，Xia JL，Gao DH，et al.Implementation and experience of a web-based allocation system with Pocock and Simon's minimization methods.Contemp Clin Trials，2010，31（6）：510-513.

［12］Cai H，Xia J，Xu D，et al.A generic minimization random allocation and blinding system on web.J Biomed Inform，2006，39（6）：706-719.

［13］Imai K，King G，Stuart EA.Misunderstandings between experimentalists and observationalists about causal inference.Journal of the Royal Statistical Society：Series A（Statistics in Society），2008，171（2）：481-502.

［14］王永吉，蔡宏伟，夏结来，等.倾向指数第二讲倾向指数常用研究方法.中华流行病学杂志，2010，31（5）：584-585.

［15］王永吉，蔡宏伟，夏结来，等.倾向指数第三讲应用中的关键问题.中华流行病学杂志，2010，31（7）：823-825.

［16］Austin PC.A comparison of 12 algorithms for matching on the propensity score.Stat Med，2014，33（6）：1057-1069.

［17］Wang Y，Cai H，Li C，et al.Optimal caliper width for propensity score matching of three treatment groups：a Monte Carlo study.PLoS One，2013，8（12）：e81045.

［18］李智文，任爱国.倾向评分加权分析法.中国生育健康杂志，2010，21（4）：251-253.

［19］李智文，任爱国.倾向评分分层和回归分析.中国生育健康杂志，2010，21（3）：186-188，封 3.

*国家自然科学基金资助（30800952）

邓 妍）