基于GIS的PM2.5浓度空间变化及对呼吸系统疾病的影响研究

湖南科技大学（411201）

李慧婷 李朝奎 毛建华 瞿志勇

基于GIS的PM2.5浓度空间变化及对呼吸系统疾病的影响研究

湖南科技大学（411201）

李慧婷 李朝奎 毛建华 瞿志勇

目的 探讨大气中PM2.5浓度空间变化及对呼吸系统疾病的影响。方法 采用GIS中的空间分析方法对某地区2009-2012年疾病统计数据和PM2.5浓度相关性进行统计分析。结果 PM2.5浓度的季节变动与人群的空间分布保持一致，与呼吸系统疾病呈现出正相关性。结论 用GIS分析PM2.5分布对人类呼吸系统疾病的影响，预测和预警效果良好，为制订PM2.5的防控措施提供科学依据。

PM2.5呼吸系统疾病 空间分析 GIS

PM2.5已成为全球大气环境研究的热点，世界卫生组织（WHO）把PM2.5定义为：大气中直径小于或等于2.5μm的大气颗粒物，常富集有毒有害的 Pb、As、Cr以及多芳烃（PAHs）等物体［1-2］。颗粒物的大小决定其最终进入人体内的部位，其中PM2.5进入人体肺泡中，对人体造成极大损害［3］。研究表明：PM2.5对人群死亡率［4］、呼吸系统疾病发病率［5］、心血管功能［6］、肺功能发育［7-8］等方面产生很大负面影响。PM2.5受空气流动影响呈现季节性变化［9］。因此研究PM2.5浓度对人类呼吸系统疾病的影响规律并提供决策依据，具有重要的意义。

国内外对于PM2.5的研究主要集中其在特征及来源［10-12］、空间分布与预测［13］等方面。国内外学者利用多种统计模拟方法对PM2.5的空间预测进行研究，Perez等［14］利用多层神经网络线性回归对城市PM2.5进行预测，得到神经网络比线性回归更具有优势；Grivas等［15］使用遗传算法和神经网络结合预测PM2.5浓度研究，与Perez得到同样结论；王敏等［16］利用BP神经网络方法对城市PM2.5浓度空间分布进行预测，得出BP人工神经网络预测模型可以揭示PM2.5浓度空间变异特征，也证实了普通克里金插值对于固定空间点准确预测PM2.5具有明显优势。以上研究都局限于采用统计模式或者传统统计插值方法对PM2.5进行研究。本文利用某地区2009-2012年卫生统计数据和PM2.5浓度的变化情况，运用GIS中空间分析方法，进行PM2.5与呼吸系统疾病就诊人数判断和拟合分析，根据所建立的分析模型对未来状况进行预测。研究结果为深入研究PM2.5分布对人类呼吸系统的影响，制订PM2.5的防控措施提供科学依据。

研究方法

1.回归分析

2.PM2.5浓度变化地理过程的自回归模型

当一个时间序列具有自相关性时，可以建立自回归模型，并且对其变化趋势进行有效地预测［17-18］。而自回归模型的建立基于平稳时间序列数据（时间序列的平稳性是指一个时间序列的统计特征不随时间推移而变化）。用自相关分析来判别该时间序列是否是平稳时间序列，如果不是，可用差分的方法把它转化为平稳时间序列。其中的一个判断方法是平稳时间序列第一个自相关系数r1比较大，与零有显著差异而r2要比r1小，其余的自相关系数与零没有显著差异［19-20］。

3.呼吸系统疾病患病情况季节性预测

（1）由于时间序列是呈线性趋势变化的，所以选择的季节预测模型是：

其中，yt+k是t+k时期的预测值；at与bt是趋势线性方程的系数；θk为季节性指标。

（2）求季节性指标。先分别计算季节系数，取平均数，得到季节性指标［19-20］。然后校正：先求校正系数，然后将季节性指标分别乘以校正系数，得到校正后的季节性指标。为消除季节变动和不规则变动，保留长期趋势，将原时间序列求三点滑动平均。即：

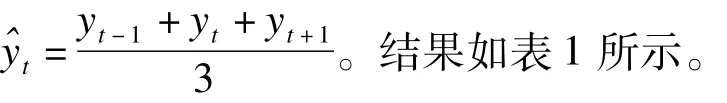
（3）运用二次指数平滑法 ，因为该时间序列比较平稳，经过试算，取0.2时误差较小。预测模型为：

UL144全序列PCR扩增共测定11例阳性 （其中1例IH-6氨基酸编码提前终止），阳性率45.8%。应用MEGA5.05软件对本研究10例阳性样本 （剔除IH-6）氨基酸序列进行进化树分析，结果分为3个基因型，包括A型 （1例），B型 （8例），C型（1例），见图 1。

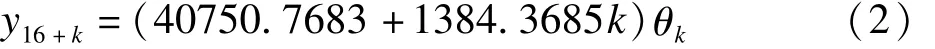
结果与分析

1.呼吸系统疾病季节变化规律分析

将收集到的呼吸系统疾病患病人数进行整理统计。按季度对收集的2009至2012年患病人数进行统计。如图1。

表1 2009-2012年呼吸系统疾病状况滑动平均数

图1 2009-2012年不同时段病人人数统计

结果显示，夏季患呼吸系统疾病人数较少，冬季最多。夏季温度较高，空气对流运动较强，有利于空气中大气微粒物的流动与扩散，与此同时，夏季降水较多，雨水能起到冲刷掉空气中大量颗粒物的效果，从而提高空气质量［21］；所选地区其他季节气候较干燥，空气相对湿度不大，较夏季降雨量偏少，而且冬季空气对流比较少，颗粒物扩散慢，颗粒物浓度较高，推断空气中颗粒物浓度的增加对呼吸系统疾病有一定的影响作用。

2.呼吸系统疾病人群空间分布

对收集到的疾病数据，根据常德市卫生局记录的病人提供的家庭地址，以及相应的邮编，手机号码等个人信息，实现病人住址的空间化。因为收集的呼吸疾病数据有限，所以以常德市所包含的县区为单位来统计数据。结果证实，武陵区、鼎城区这两个地区病人人数比较高。

3.呼吸系统疾病患病状况与颗粒物浓度相关分析

选取PM2.5的浓度为要素x，呼吸系统疾病患病人数为要素y。所获取的PM2.5浓度为日数值。计算得到 rxy＝0.8482，p＜0.05。结果表明，PM2.5的浓度与呼吸系统疾病患病人数存在正相关关系。

4.PM2.5浓度变化地理过程的自回归模型分析

一阶自相关系数

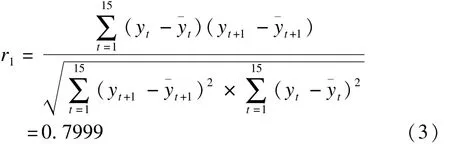
由此得到其一阶自相关系数具有高度的显著性。同理，得到 r2＝0.5377，当 α＝0.001时，r0.001＝0.7800。所以其二阶自相关系数相关性并不显著。对于该序列可以建立一阶线性自回归模型。用最小二乘法来估计模型参数：

得到：

计算出＾φ0＝704.2147，＾φ1＝0.9658。拟合自回归方程为：＾yt＝704.2147+0.9658yt-1，计算得，F＝23.099。由于F＞＞F0.01（1，13）＝9.07，该一阶自回归方程在置信水平下是显著的。

5.呼吸系统疾病患病情况季节性预测

2013年度的呼吸系统患病人数为：

为评价预测模型的精度，本文中采用了均方差（MSE）、平均绝对误差（MAE）、相关系数三个评价指标。MSE、MAE越小，表明预测结果越准确；R2越接近1，表明预测值与观测值相关或越接近。结果如表2。

表2 基于评价指标的预测精度检验结果

结 论

1.本文以季度为时间单位对收集到的数据进行统计分析，同时，采用ArcGIS软件将病人空间分布可视化表达。统计表明：冬季呼吸系统疾病发病人数最多。

2.PM2.5浓度变化与呼吸系统疾病患病人数变化有直接正相关关系。因此，降低颗粒物的浓度能减少呼吸系统疾病的患病率。

3.通过预测模型精度各指数评价，可得到模型精度比较高。

4.受以下两点条件的制约，模型精度有待进一步探究：

（1）呼吸系统疾病发病情况影响因素错综复杂，本研究只是针对近年来空气质量恶化的同时呼吸系统疾病发病状况显著增加这一情况进行质疑，进而对雾霾形成的一大主要成因PM2.5与呼吸系统疾病发病状况之间的关系进行探讨。以此建立的模型必定无法充分说明呼吸系统疾病趋势的具体变化。因此需要进行更加充分的现场调查和分析，从而全面深入了解呼吸系统疾病患病的影响因素提高预测模型的质量。

（2）自回归模型需要的历史数据比较容易获得，但存在一定的滞后性，使得异常条件下的预测存在较大的误差，若能与其他方法联合进行预测，应该会取得更好的效果。

［1］孙志豪，崔艳平.PM2.5对人体健康研究概述.环境科技学报，2013，26（4）：75-78.

［2］邵龙义，时宗波，黄勤.都市大气环境中可吸入颗粒物的研究.环境保护.2000（1）：24-29.

［3］黄怡民，付川.我国PM2.5污染特征的研究进展.重庆三峡学院学报，2013，29（145）：105-109.

［4］Zeger SL，Dominicl F，Mcdermott A，et al.Mortality in the medicare population and chronic exposure to fine particular air pollution in urban centers（2000-2005）.Environmental Health Perspectives，2008，116（12）：1614-1916.

［5］Zhang JJ，Hu Wei，Wei FS，et al.Children's respiratory morbidity prevalence in relation to air pollution in four Chinese cities.Environmental Health Perspectives，2002，110（9）：961-967.

［6］Vallejo M，Lerma C，Infanet O，et al.Personal exposure to particulate matter less than 2.5 um in Mexico City：a pilot study.Journal of Exposure Analysis and Environmental Epidemiology，2004，14（4）：323-32.

［7］Gauderman WJ，Avol E，Gilliand F，et al.The effect of air pollution on lung development from 10 to 18 years of age.New England Journal of Medicine，2004，351（11）：1057-1067.

［8］Jedrychowski WA，Perera FP，Maugeri U，et al.Effect of prenatal exposure to fine particulate matter on ventilatory lung function of preschool children of non-smoking mothers.Paediatric and Perinatal Epidemiology，2010，24（6）：492-501.

［9］王钊，韩斌，倪天茹，等.天津市某社区老年人PM2.5暴露痕量元素健康风险评估.环境科学研究，2013，26（8）：913-918.

［10］董海燕，古金霞，姜伟，等.天津市颗粒物中元素化学特征及来源.环境监测管理与技术，2012，24（1）：25-28.

［11］孙玉伟，周学华，袁琦，等.济南市秋末冬初大气颗粒物和气体污染物污染水平及来源.环境科学研究，2012，25（3）：245-252.

［12］李旭芳，初钧晗，于令达，等.北京市城区单监测点 PM2.5质量浓度变化特征.北京师范大学学报（自然科学版），2011，47（3）：258-261.

［13］郭涛，马永亮，贺克斌.区域大气环境中PM2.5／PM10空间分布研究.环境工程学报，2009，13（1）：147-150.

［14］Perez P，Trier A，Reyes J.Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago，Chile.Atmospheric Environment，2000，34（8）：1189-1196.

［15］Grivas G，Chaloulakou A.Artificial neural network models for prediction of PM10 hourly concentrations，in the Greater Area of Athens，Greece.Atmospheric Environment，2006，40（7）：1216-1229.

［16］王敏，邹滨，郭宇，等.基于BP人工神经网络的城市PM2.5浓度空间预测.环境污染治理，2013，35（9）：63-70.

［17］林炳耀.计量地理学概论.北京：高等教育出版社，1985.

［18］徐建华.计量地理学.北京：高等教育出版社，2006.

［19］沈斌，姚敏，温长洋.一种基于混合模型的时间序列数据挖掘系统.中国矿业大学学报，2003，32（3），284-288.

［20］Box GEP，Jenkins GM.时间序列分析预测与控制.北京：中国统计出版社.1997.

［21］杨维.北京城区PM2.5浓度空间变化及对呼吸健康影响.首都师范大学硕士学位论文，2013.

邓 妍）