需求不确定条件下的制造商订单分配模型

徐 辉，侯建明

(上海理工大学管理学院，上海 200093)



需求不确定条件下的制造商订单分配模型

徐 辉1，侯建明2

(上海理工大学管理学院，上海 200093)

制造商的订单分配作为供应链模型微观层面的重要组成部分，对提升整个供应链效率有很大影响，但需求层面的不确定因素加大了订单分配的难度。以按比例分配为原则，讨论在需求不确定条件下完全信息与不完全信息两类多供应商-单制造商的订单分配模型。重点研究完全信息条件下各方的分散决策和集中决策，由于后者能避免各参与方对其他决策方的边际影响，所以能够实现供应链总利润的最大化；其次又将不完全信息引入模型，讨论制造商如何通过折算因子结合已有信息对供应商的私人信息进行估计，进而做出决策。最后以需求服从正态分布为例对两类模型进行验证。

需求不确定；订单分配；不完全信息；供应链模型

1 引言

在全球经济一体化的今天，供应链管理作为一种高效的管理方法，在很多企业得到广泛应用。随着ERP系统在企业中的普及，准时制和均衡化生产越来越普遍地应用到实际生产中，从最初仅对库存进行管理，发展到现在强调从计划、采购、制造等各个环节都予以配合，大大降低了供应链管理中供给端的不确定性。与此同时，全球经济联系日趋紧密、政策变化周期越来越短、消费者需求转变开始加速，受此影响，需求方面的不确定性在实际中变得愈发突出，因此近年来从需求不确定角度对供应链的研究逐渐增多[1-3]。此外，已有文献对供应链模型的研究多集中在宏观的供应链管理以及如何选择最合适的供应商上，而微观层面的订单分配等问题还未得到足球重视。实际生产中，订单分配的低效率一直制约着供应链利润的提高。因此，对需求不确定条件下的订单分配模型进行研究，对完善供应链模型理论有着非常重要的实际意义。

Clark,Kawtummacha,Sodenkamp等[4-6]将考察库存分配、挑选供应商的层次分析等方法移植到订单分配上，验证了此类优化组合的算法可以降低制造商的成本、提高供应商的准时交货率[4-6]。Guo Zhaoxia等[7]学者在此基础上对多目标的订单分配问题进行了优化。Amin等[8]引入了之前文献中被忽视的一些定性因素，建立了同时兼顾定性和定量的模糊SWOT分析和模糊线性规划。不过此类研究只考虑了单个制造商的最优，未能结合整个供应链来考察，忽视了制造商的收益增加可能是建立在供应商收益减少的基础之上。Lee等[9]最先注意到处于供应链下游的企业为了获得更大利润，通常会上报比实际需求更高的数量，这种不真实的需求信息会沿着供应链向上逐级放大，并最终导致供应和库存的高风险，从而降低整个供应链的利润。此外，在分配机制方面，张旭梅等[10]设计了一个以诱导供应商说实话为目的的激励约束机制，根据历史数据分析供应商上报订单信息的真伪，并对上报虚假订单的供应商进行处罚。不过 Cachon等[11]在研究容量选择和分配机制时发现，在价格固定的时候，一个允许下游企业夸大订购量的机制优于一个揭示下游企业私人信息的“实报”机制，即实报机制未必是一个好的目标。徐贤浩等[12]在研究短生命周期产品的时候也发现，通过对市场开发和提高促销的努力水平，可以提高市场的最终需求，实际决策中设计一个合理的激励机制而不是诱导供应商实报，对提高整个供应链的利润更重要。

以上文献主要讨论的是确定性问题，其中徐贤浩等将不确定性引入实际问题，不过未进一步展开讨论。Gurnani[13]通过研究半导体制造行业考察产出方面的不确定性。杨文胜等[14]建立了制造商、供应商分别以奖金激励、交货时间为决策变量的Stackelberg模型，并分析了供应商完成订单的响应函数服从指数分布时制造商和供应商的决策。李果等[15]系统地分析了不确定交货条件下的供应链模型，建立了一个考虑缺货成本、库存成本、残值收益等的两供应商-单制造商的协同供货模型，并用算例说明了如何通过调节订货批量和单位处罚成本来达到供应链利润的最大化。目前此类文章只引入了供给方面的不确定性，并且其模型仅考查了完全信息条件下博弈各方所做的决策，未对不完全信息进行分析。

鉴于需求方面的不确定性成为问题的主要方面，本文拟对制造商需求不确定条件下的订单分配问题做一些探索。由于供应链存在私人信息时线性的按比例分配机制有很好效果[16]，因此本文选择这种生产中也很常见的按比例分配规则，借鉴吴忠和等[17]对不确定问题的处理，建立基于完全信息和不完全信息两种条件下的多供应商-单制造商的供应链模型。重点研究了完全信息条件下模型各方的分散决策和集中决策；其次又在不完全信息条件下做了一些探索：受文献[11]启发，模型假设制造商不设法去了解各供应商的私人信息，同时借用在刻画热传导、金融风险等不确定情况时常用的折算因子法，分析制造商如何通过折算因子并结合已有信息对供应商的私人信息进行估计。最后通过一个算例来验证模型，并得出结论。

2 模型建立

2.1 问题的描述

制造商的订单分配一直是实际生产中的难题：订单分配效率过低，一方面供应商的产能得不到有效利用，不利于制造商和供应商的合作；另一方面为满足市场需求，制造商不得不开发更多供应商，从而造成不必要的浪费。实际生产中订单分配的具体流程通常是：首先，制造商确定一种分配规则；其次，制造商和供应商根据自身实际情况结合分配规则做出决策；最后，制造商根据决策结果并按照分配规则对订单进行分配。其中，制造商和供应商的决策是订单分配的核心与难点。当制造商面临的市场需求不确定时，订单分配问题更加复杂。本文讨论制造商和供应商在特定的分配规则下，应做出何种决策才能达到各自利润或者供应链总利润的最大化。

2.2 模型假设与变量说明

本文考察由n个供应商Si(i=1,2,…,n)和一个制造商M构成的供应链模型。首先制造商根据市场对产品的需求得出自身对部件的需求；其次制造商把对部件的需求按照一定的分配规则拆分成若干订单，并分配给n个供应商；然后供应商根据被分配的订单安排部件生产，并销售给制造商；最后制造商组装成产品销售给市场。并对模型作如下假设：

(1)各参与者是理性的：以利润最大化为目标。

(2)制造商M对部件的需求Q是随机的：记Q的概率密度函数为f(q)，分布函数为F(q)。

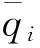
(4)成本假设：供应商Si生产部件的可变成本为Ci，固定成本为FCi。对于供应商不能按时完成的部件，制造商可以从其他市场高价购买该部件，记此价格为调货成本Ch。

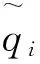
本文涉及的符号标记见表1：

表1 符号标记

2.3 基本模型

2.3.1 供应商模型

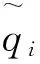
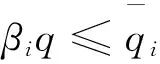
根据2.2中各参数的定义，当市场需求Q=q时，供应商Si的利润函数为：

(1)

2.3.2 制造商模型

同理：制造商的决策变量为单位处罚Cu，当市场需求Q=q时，制造商的利润函数为：

(2)

其中，第一项为供应商按时交货部分对应的制造商毛利润，第二项为供应商未能按时交货部分对应的制造商毛利润，第三项为制造商固定支出。

最后，当制造商面临的市场需求Q是随机变量时，以上两模型的决策目标应为最大化相应利润函数的期望值。下文分完全信息和不完全信息两种情况对模型进行具体讨论。

3 完全信息条件下的模型分析

根据供应链管理理论，供应链各节点企业进行深度合作，建立战略合作关系，可提高沟通效率，降低供应链总成本，最终增加整体收益。同时现代信息技术的快速发展，也为战略合作企业进行信息共享创造了客观条件。当影响决策的相关信息为所有企业掌握，此时认为企业占有完全信息。因此完全信息条件下的模型适用于进行战略合作企业间的决策分析。

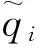
3.1 分散决策下的模型分析

3.1.1 供应商决策分析

市场需求Q的概率密度函数为f(q)，由(1)得到供应商Si的期望利润函数：

(3)

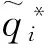
(4)

(5)

3.1.2 制造商决策分析

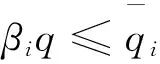
所以，由(2)得到制造商的期望利润函数，并化简得：

(6)

对(6)式进行一阶求导：

(7)

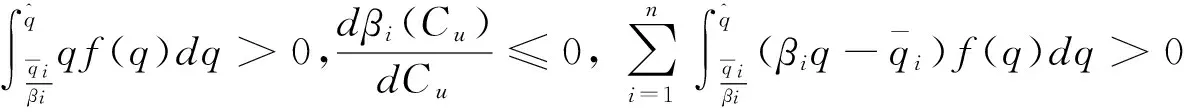
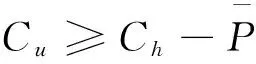
3.1.3 分散决策下的模型分析

上述两种情况，都是由于孤立地进行自身决策，而忽略了对其他参与方的边际影响，导致个体理性和集体理性间的冲突，即个体之间进行分散决策达不到供应链整体利润的最大化。在下面的集中决策下，可以看到该问题得到了很好的解决。

3.2 集中决策下的模型分析

在完全信息条件下，作为模型主方的制造商拥有决策所需的所有信息，所以其可以进行集中决策以实现供应链的最大利润，最后各方再进行供应链总利润的分配。

首先考虑集中决策模型必须满足的两个前提条件，即参与约束IR和激励相容约束IC。其中，参与约束IR：各供应商和制造商都可以选择不加入供应链，即保留利润为0。激励相容约束IC：各供应商和制造商组成的供应链总利润之和达到最大化，此时亦大于分散决策下供应链的总利润。即：

(8)

其中：

因此，集中决策下的模型可以转化为：

(9)

其中：βi=βi(β1,β2,…,βi-1,βi+1,…,βn,Cu),i=1,2,…,n

对(9)构造拉格朗日函数求得(β*,Cu*)是方程(9)的最优解后，即实现了供应链利润的最大化，博弈各方可以通过谈判实现供应链内部利润的转移，这取决于各方谈判力度的大小。

由完全信息条件下的模型分析可知，当各方都不存在私人信息时，作为模型主方的制造商不仅可以对最优处罚进行决策以实现制造商的最优期望利润，还可以对处罚和订单分配都进行决策，从而实现整个供应链的最大期望利润。即进行深度战略合作的企业之间，应该多进行集中决策，处于核心地位的企业应该站在整个供应链层面发挥更大的决策作用。

4 不完全信息条件下的模型分析

实际生产中，虽然组成供应链会让制造商对供应商的情况有更多了解，但决策各方依然很难占有所需要的全部信息。这可能是由于信任机制不健全，相关方不愿意进行信息共享；或信息化建设不健全，信息获取的成本过高；甚至是法律法规设置的壁垒等。当决策需要的信息不能为企业完全掌握时，即为不完全信息条件，此时模型分析适用于未能进行战略合作企业间的决策。

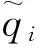
此时制造商M依然为主方，在第一阶段确定处罚Cu；供应商Si为从方，在第二阶段选择自己的最优份额βi。由于制造商缺少各供应商具体的实际最高产量信息，因此不能再确定一个使供应链总利润达到最大的最优处罚Cu*。即在这种情况下，博弈各方只能进行分散决策。此时供应商的决策分析同3.1.1，但制造商的决策分析有了新的特点。

4.1 制造商决策分析

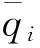
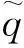
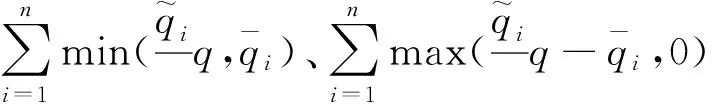
所以，制造商的决策是最大化如下期望利润函数：

化简得：

(10)

对(10)式进行一阶求导：

(11)

因为(11)恒大于0，所以制造商的期望利润函数没有最大值，E[∏M(Cu)]随着Cu的增加而增加，但制造商增加Cu的意愿受制于其在行业内的垄断程度：其在行业中市场份额越大，增加Cu的意愿和能力越强。制造商确定处罚Cu之后，各供应商再上报自身的最优份额。

由不完全信息下的模型分析可知，在仅进行一般合作的企业之间，处于供应链核心地位的企业会有更大动力增加处罚以提高其利润。同时由于效率损失的存在，不完全信息下供应链总利润低于完全信息下总利润，因此核心企业利润的增加以非核心企业利润的减少为前提。因此，若非核心企业能加强与核心企业合作，进行更多的信息共享，可提高供应链效率，增加自身利润。

现实生活中商品的需求大都服从正态分布，因此在如下算例中以正态分布为例对上述模型进行实证分析。

5 算例

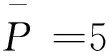
因为制造商M对部件的需求Q服从正态分布，其中E(Q)=10000：

(1)在完全信息条件下

将算例中数据代入(9)，并将其对βi和Cu求导得到：

当制造商选择的单位处罚为Cu=5，供应商S1和S2的最优比例分别为：β1=0.6695，β2=0.3305，此时供应链的总利润最大为118573。

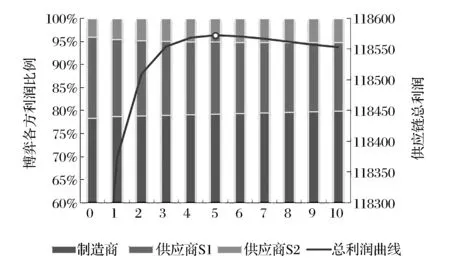
图1 完全信息下博弈各方利润与总利润

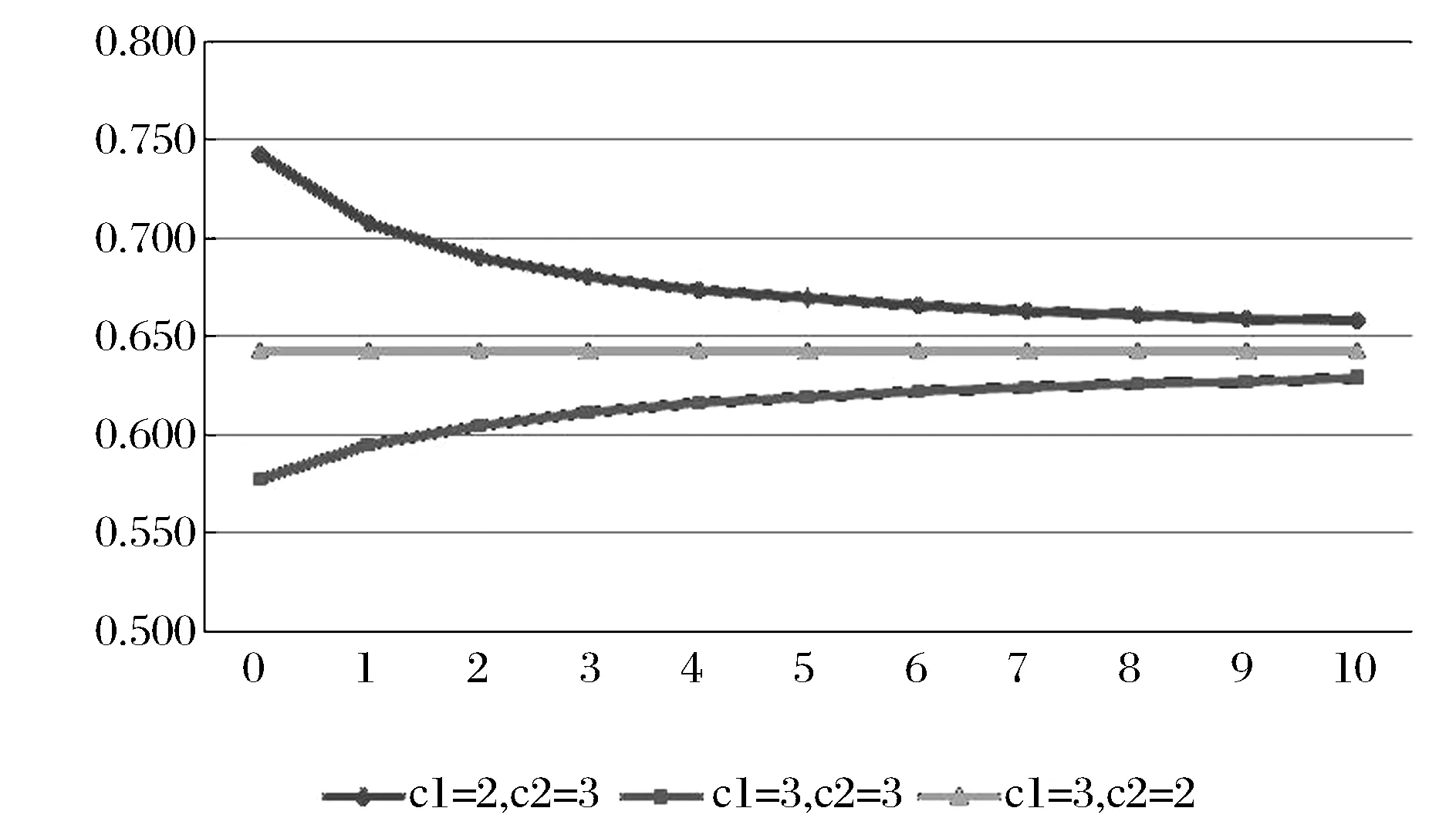
图2 供应商S1在不同成本下的最优比例

由图1可以看出，在题设条件下，随着处罚Cu从0开始增加时，最初整个供应链的利润增加很快，这主要是由于增加处罚，修正了分配给供应商S1的过多订单。由于S1的可变成本较小，所以去除可变成本之后的剩余利润更大；当处罚很小进而S1面临的缺货成本很小时，S1会要求更多的订单。从图2的最上一条曲线可以看出，S1在处罚较小的情况下，获得了远超其实际最高产量份额的订单，造成订

表2 惩罚D=10时，各供应商最优比例与实际分配比例情况(C1=2,C2=3)

单分配不合理：可能出现S2有闲置产能，同时S1未完成的订单数量较大，从而制造商不得不从其他市场高价调货，最终使整个供应链的利润外流。

随着处罚Cu从5继续增加，供应链总利润又开始下降，这主要是由于继续增加处罚，供应商S1要求并分配到的订单低于其最优比例。因为处罚很大进而供应商面临的缺货成本很大时，供应商愿意分配到的比例趋于实际最高产量的比例，从而造成S1可变成本较低的优势并未体现。

其中供应商S1在整个供应链的利润占比随处罚Cu的增大逐渐下降，可以看出处罚对较低可变成本的供应商影响更大。供应商S1的可变成本较供应商S2低，可认为S1的生产效率更高，最终其最优的分配比例高于其实际最高产量占总最高产量的比例，这一结论也和经验相符。在图2中，对两供应商可能的不同成本做了分析，得出结论：较低可变成本的供应商，其最优分配比例高于其最高产量占总最高产量的比例；反之反是。具体的差别和单位处罚Cu有关，单位处罚越高，最优分配比例越接近其最高产量的占比。

(2)在不完全信息条件下

由(11)知，制造商的期望利润E[∏M(Cu)]随着Cu的增加而增加。考虑Cu在[0,Ch]内，各供应商不会中止合作的情况，此时制造商选择Cu=Ch=10，各供应商的最优选择和实际分配情况见表2。

从表2可以看出：不完全信息条件下，各供应商的最优比例均高于完全信息条件下集中决策的最优比例，这表明在分散决策下，各供应商都有增加自身份额的动力；在实际分配中，由于各供应商都倾向于多报自身份额，最后虚报的份额有部分抵消，使实际分配的值趋于使整个供应链利润最大的最优比例，即最终虽然各供应商的利润未能达到最大值，但实现的供应链总利润大于按照各供应商期望分配比例时的总利润。

折算因子δ取不同值时，制造商做决策时预期的利润与实际利润的比较如表3所示。

当δ=1时，制造商完全相信供应商上报的数据，可以看到此时预期利润和实际利润有较大误差；当δ=0.9454时，此时δ为各供应商最优比例和的倒数，但两利润之间仍有一些误差；δ=0.9432时，此时的预期较准确。实际生产中，制造商可以根据预期利润与实际利润的差值来调整折算因子使预期利润更接近实际值，从而达到理想的分配状态。

表3 制造商的实际利润以及折算因子δ取

6 结语

本文讨论了制造商面临的市场需求为不确定时，在按比例分配规则下供应链各方在完全信息和不完全信息两种情况下如何进行决策并按照规则分配订单，最终实现各自利润或供应链总利润的最大值。主要得出以下结论：(1)供应商的风险承受能力主要取决于各自的产能和可变成本，同时供应商要求订单的意愿与自身的风险承受能力成正比，与制造商选择的单位处罚成反比。(2)在一定范围内，制造商有增加单位处罚的动力；但从整个供应链角度考察，单位处罚的增加可能会导致供应链总利润的减少；在处罚一定的情况下，各供应商都有多报自身份额的倾向。(3)在完全信息条件下，分散决策由于未考虑自身决策对其他参与方的边际影响而导致供应链有效率损失，此时集中决策可实现整个供应链总利润的最大值。(4)在不完全信息条件下，由于决策方缺少进行最优决策的完整信息，供应链总利润达不到最大值；不过由于各供应商都有多报自身份额的倾向，导致最终按比例分配的供应链总利润，虽然不如完全信息条件下，但优于各供应商独自决策的结果。

最后，本文模型的建立以供应商按照订单进行均衡化生产为前提，未考虑供应商的实际最大产量可能存在一定弹性，后续讨论可以放宽这一限制；其次，本文对不完全信息模型仅做了一些初步的探讨，用供应商上报的总最大产量通过折算因子对其实际总最大产量进行估算，后续的分析可以从更多角度对此做更深入的研究。

[1] He Yuanjie, Zhang Jiang. Random yield risk sharing in a two-level supply chain[J]. International Journal of Production Economics, 2008, 112(2):769-781.

[2] 凌六一, 郭晓龙, 胡中菊, 等. 基于随机产出与随机需求的农产品供应链风险共担合同[J]. 中国管理科学, 2013, 21(2):50-57.

[3] 张克勇, 侯世旺, 周国华. 不确定需求下供应链定价延迟策略研究[J]. 管理工程学报, 2014, 28(1):195-201.

[4] Clark A J, Scarf H. Optimal policies for a multi-echelon inventory problem[J]. Management Science, 2004, 50(12):1782-1790.

[5] Kawtummacha R, Nguyen V H. Order allocation in a multiple-supplier environment[J]. International Journal of Production Economics, 2005(93-94):231-238.

[6] Sodenkamp M A, Suhl L. A multicriteria multilevel group decision method for supplier selection and order allocation[J]. International Journal of Strategic Decision Sciences, 2012, 3(1):81-105.

[7] Guo Zhaoxia, Wong W K, Leung S Y S. A hybrid intelligent model for order allocation planning in make-to-order manufacturing[J]. Applied Soft Computing, 2013, 13(3):1376-1390.

[8] Amin S H, Razmi J, Zhang Guoqing. Supplier selection and order allocation based on fuzzy SWOT analysis and fuzzy linear programming[J]. Expert Systems with Applications, 2011, 38(1):334-342.

[9] Lee H L, Padmanabhan V, Whang S. Information distortion in a supply chain: The bullwhip effect[J]. Management Science, 1997, 43(4):546-558.

[10] 张旭梅, 李国强, 张翼. 供应链中供应商订单分配的不完全信息动态博弈研究[J]. 管理学报, 2006, 3(5):519-523.

[11] Cachon G P, Lariviere M A. Capacity choice and allocation: Strategic behavior and supply chain performance[J]. Management Science, 1999, 45(8):1091-1108.

[12] 徐贤浩, 聂思玥. 基于短生命周期产品的供应链订货策略的博弈研究[J]. 管理工程学报, 2007, 21(3):44-48.

[13] Gurnani H. Optimal lot-sizing policy with incentives for yield improvement[J]. IEEE Transactions on Semiconductor Manufacturing, 2005, 18(2):304-308.

[14] 杨文胜, 马士华, 李莉. 供应链中准时采购的Stackelberg模型及决策[J]. 系统工程理论方法应用, 2005, 14(1):68-73.

[15] 李果, 马士华, 高韬, 等. 不确定交货条件下两供应商-单制造商协同供货模型[J]. 管理工程学报, 2011, 25(3):91-99.

[16] Deshpande V, Schwarz L B. Optimal capacity choice and allocation in decentralized supply chains[M]. West Lafayette ：Purdue University, 2005.

[17] 吴忠和, 陈宏, 赵千, 等. 两零售商竞争下多因素同时扰动的供应链协调研究[J]. 中国管理科学, 2012, 20(2):62-67.

Manufacturer's Order Allocation Model under Demand Uncertainty

XU Hui1， HOU Jian-ming2

(School of Management, University of Shanghai for Science and Technology,Shanghai 200093,China)

As an important part of the supply chain model at the micro level, manufacturer’s order allocation has a great influence on improving the efficiency of the supply chain. In the meanwhile, demand uncertainty ,such as the policy cycle shortening and consumption patterns changing, increases the difficulty of the manufacturer’s order allocation. However, supply chain management disruption caused by demand uncertainty has not been generally studied in the current literature. In order to maximize their profits or total supply chain profits under certain allocation rule, how supply chain participants should make decisions, which is discussed especially in this paper. Some positive explorations are made in order allocation models, which demand uncertainty is considered and incomplete information is introduced into the supply chain participants. Two kinds of the multi-suppliers and one-manufacturer models are analyzed within the method of proportional distribution under demand uncertainty. A supply chain model is emphasized on the study of decentralized decision and centralized decision based on complete information, which concludes that the latter can maximize the interest of supply chain because of the avoidance of marginal effect caused by one participant to another when making decisions. And then, another model is established upon incomplete information, which pays emphasis on the decision-making mechanism of manufacture based on its estimate of suppliers’ private information with discounting factor and existing information. In addition, the risk tolerance of suppliers depends mainly on their production capacities and variable costs, and the intention of supplier getting order is proportional to the risk tolerance, inversely to the unit punishment. Finally, the aforementioned two models are validated by an example of demand obeying normal distribution, given that the demand of most goods is normal distribution in real life.

demand uncertainty; order allocation; incomplete information; supply chain model

1003-207(2016)03-0080-09

10.16381/j.cnki.issn1003-207x.2016.03.010

2014-01-09；

2015-01-26

简介：徐辉(1986-)，男(汉族)，安徽阜阳人，上海理工大学管理学院硕士研究生，研究方向：博弈论、工业经济、供应链管理,E-mail:xuhui050505@163.com.

F273.1

A