期望效用视角下的风险对冲效率
2016-12-27黄金波李仲飞周鸿涛
黄金波,李仲飞,周鸿涛
(1. 广东财经大学金融学院,广东 广州 510320;2. 中山大学管理学院,广东 广州 510275)
期望效用视角下的风险对冲效率
黄金波1,李仲飞2,周鸿涛1
(1. 广东财经大学金融学院,广东 广州 510320;2. 中山大学管理学院,广东 广州 510275)
与传统文献将风险下降比率作为风险对冲效率指标不同,本文引入期望效用理论来比较最小方差对冲策略、最小在险价值(VaR)对冲策略和最小条件在险价值(CVaR)对冲策略的对冲效率,从而将人们的风险态度同对冲策略选择联系起来,以实现不同风险态度的投资者选择不同风险对冲策略的目的。借用风险中性效用函数、二次效用函数和CARA效用函数,本文严格证明:在这三种对冲策略中,最小方差对冲策略过于保守,最小VaR对冲策略最为激进,风险厌恶程度大的投资者偏好最小方差对冲策略,风险中性投资者和风险厌恶程度小的投资者更偏好最小VaR对冲策略,最小CVaR对冲策略介于二者之间。
风险对冲;期望效用;风险态度;在险价值;条件在险价值
1 引言
金融风险管理是现代金融学研究和关注的基本问题,也是金融工程与风险管理领域的研究热点和前沿问题。根据研究框架的不同,当前的风险对冲研究大致可分为两大类[1]:基于风险最小化模型的研究和基于效用最大化模型的研究。基于风险最小化模型的研究主要是寻找各种更加合理的风险指标测度对冲组合的风险,然后求出风险最小的对冲组合。这类研究隐含地假设人们是完全的风险规避者,仅关心风险而不关心收益,风险对冲的目标是让风险达到最小。根据风险度量指标的不同,这类研究主要包括基于方差指标的研究[2-4],基于mean-Gini系数的研究[5-6],基于广义半方差 (Generalized Semivariance, GSV)的研究[7],基于VaR和CVaR的研究[8-12]以及基于AS指标的研究[13]等。基于效用最大化模型的研究主要是最大化包含风险与收益的某个效用函数,通常这类效用函数需要事前赋予风险与收益某个权衡系数,该系数代表人们对风险的厌恶程度,这类研究可见文献[14-16]。以上两类研究都存在一定的不足,前一类研究的不足在于最小化某个测度风险的客观指标,而完全不考虑人们的主观风险态度(或隐含人们是完全的风险规避者),但在实际生活中,人们的风险厌恶程度是不同的,不同的风险态度显然会影响对冲策略的选择。后一类研究的不足在于效用函数里权衡系数的确定没有科学的标准,不同的系数会得出不同的对冲策略。另外,虽然效用理论是在不确定环境下更为系统和严谨的决策理论,但基于效用最大化的风险对冲策略却很难在实践中运用,主要原因是效用理论下的风险隐含在效用函数形式里,而效用本身是很难说清楚的抽象概念,所以效用函数形式的设定具有较强的主观性。
因此,为弥补以上两类研究的不足,同时吸收两类研究各自的优点,本文首先基于风险最小化模型得到对冲策略,然后运用期望效用理论来比较各个对冲策略的对冲效率,这样就可以把人们的风险态度同对冲策略选择联系起来,实现不同风险态度投资者选择不同的风险对冲策略的目的。与传统的风险最小化模型研究的不同点在于我们不是以风险下降比率作为对冲效率衡量标准,与传统的效用最大化模型的不同点在于我们不需要事前设定权衡系数,即不需要设定精确的风险厌恶系数,我们只需要把投资者大体分为风险厌恶程度高、中、低三类即可。这在现实生活中是容易实现的,也是业界常用的方法,例如当前很多投资者在购买投资产品之前需要进行风险承受能力评估,经纪人根据风险承受能力评估的得分把投资者分为风险承受能力弱、中、强三类,分别对应着风险厌恶程度高、中、低。
在风险最小化模型中,首要的问题是确定风险度量指标,根据人们对风险的不同理解,理论界和实务界提出了多种风险度量指标。其中,最经典的是Markowitz[17]提出的方差,而当前最受欢迎的是Morgan提出的在险价值 (Value-at-Risk, VaR)及Rockafellar和Uryasev[18]提出的条件在险价值 (Conditional Value-at-Risk, CVaR)。VaR是指在给定置信水平下,在未来特定期间内,资产或资产组合所遭受的最大可能损失[19],CVaR是指超过VaR水平的所有损失的数学期望。刘俊山[20]详细讨论了VaR和CVaR的理论性质和应用价值。他指出,虽然CVaR指标的理论性质优于VaR,但是CVaR的后验检测不易实现,因而,VaR目前仍然是业界广为使用的风险度量工具[21-22],而CVaR是学术界公认的理论性质比VaR更优的风险指标[23]。如今VaR与CVaR已经一起被写入巴塞尔协议III作为风险监管工具。基于此,本文主要研究最小方差、最小VaR和最小CVaR的风险对冲问题。
2 最优对冲比率
有关风险对冲的具体问题有很多,本文集中研究期货现货的风险对冲问题。设现货资产和期货资产的收益率分别为r1,r2,r1的均值和标准差为μ1,σ1,r2的均值和标准差为μ2,σ2。1单位现货资产多头和h单位期货资产空头所构成的组合收益率rp(h)可表示为:
rp(h)=r1-hr2
(1)
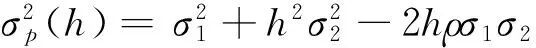
设对冲组合的收益率rp(h)的概率分布函数为F(x,h),在给定的置信水平1-α下,对冲组合的在险价值VaR(h)数学表达式为[19]:
VaR(h):=-inf{x∈R:F(x,h)≥α}
(2)
置信水平1-α是事先给定的,一般由投资者根据自身偏好设定或由监管机构设定。在分布函数F(x,h)满足连续性的条件下,VaR(h)为rp(h)的下侧α分位数的相反数。在VaR基础上,对冲组合的CVaR的数学表达式为[18]:
CVaR(h):=-E[rp(h)|rp(h)≤-VaR(h)]
(3)
最小VaR(或CVaR)对冲策略就是寻找使得组合的VaR(或CVaR)达到最小的对冲比率h。在rp(h)服从正态分布的假设下,相应的VaR(h)和CVaR(h)可以表示为均值和标准差的线性函数[11-12],即:
VaR(h)=-zασp(h)-μp(h),CVaR(h)=(φ(zα)/α)σp(h)-μp(h)
(4)
其中σp(h)为组合收益率的标准差,zα为标准正态分布的下侧α分位数,φ(·)为标准正态分布的密度函数。
在正态分布下,基于最小方差、最小VaR和最小CVaR的风险对冲模型可统一表示为:
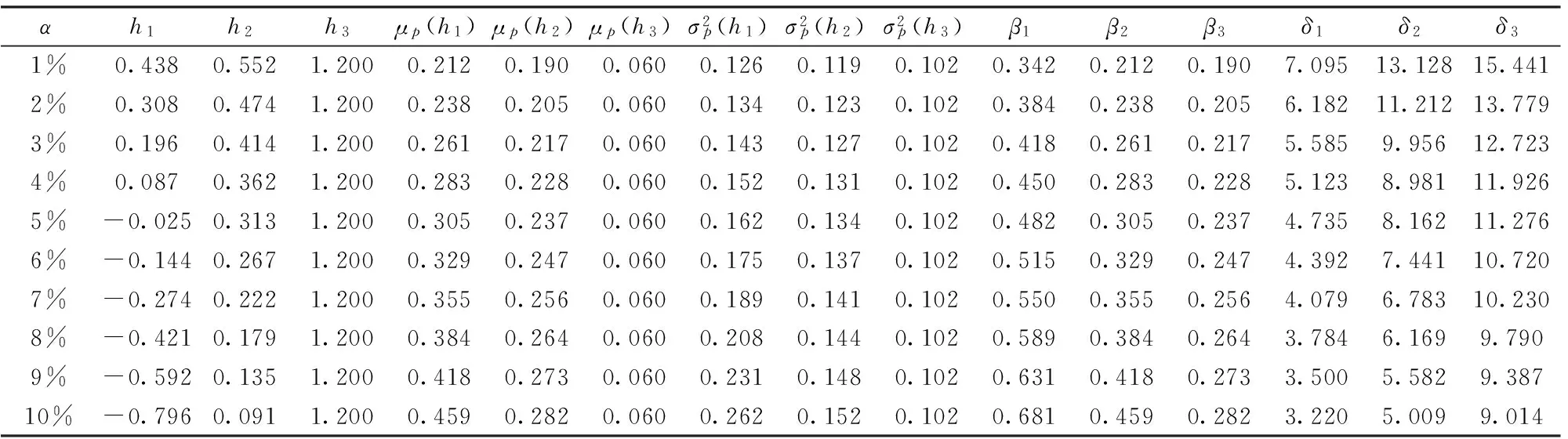
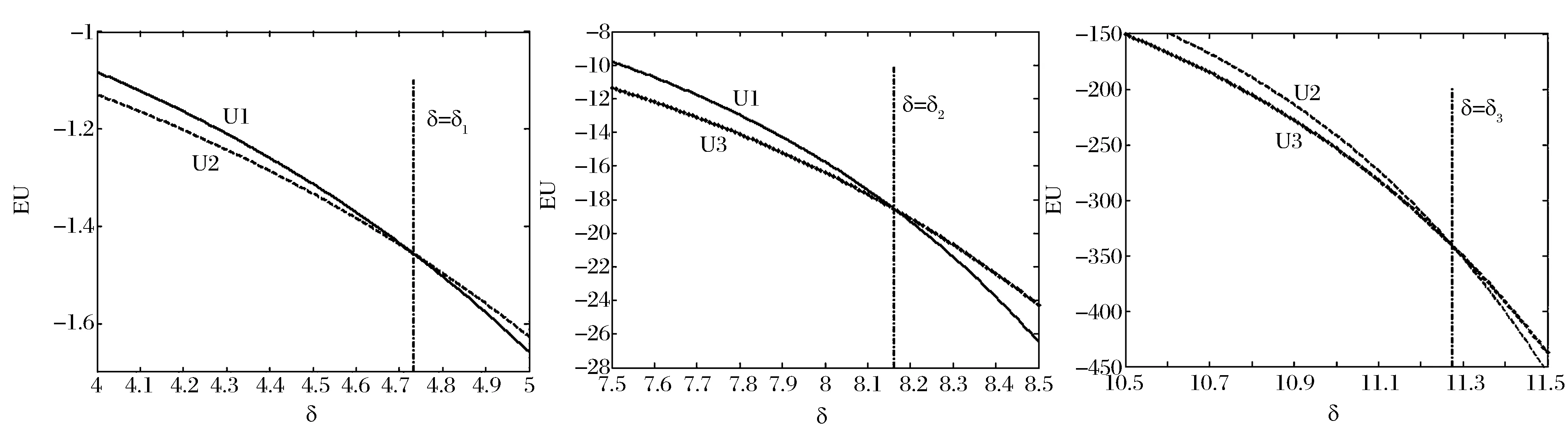
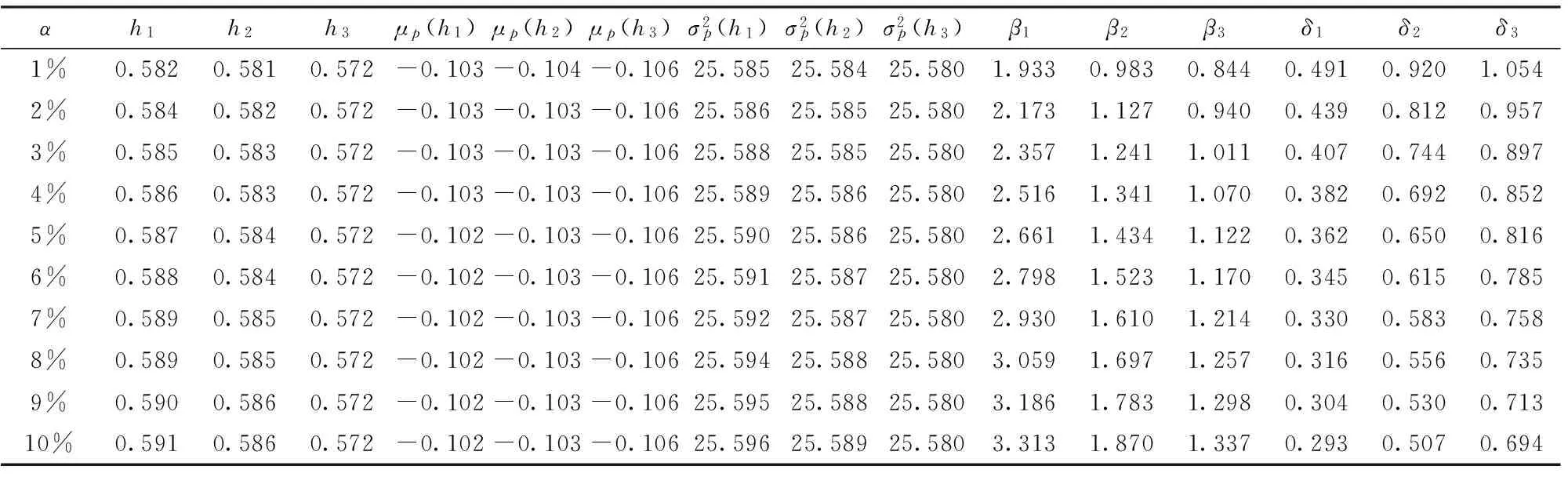
其中k为常数。当k1=-zα时,p1为最小VaR模型,当k2=φ(zα)/α时,p1为最小CVaR模型,当k3=+∞时,p1为最小方差模型。根据标准正态分布的性质,不难发现,当α≤0.5时,0 (5) 二阶导数满足以下条件: (6) (7) h1,h2,h3分别对应最小VaR、最小CVaR和最小方差模型的最优对冲比率。根据(7)式,可得如下三个性质。 证明:(7)式两边对ci求导可得: (8) 所以,当μ2>0时,∂hi/∂ci<0,由c1≥c2≥c3,可得h1≤h2≤h3;当μ2<0时,∂hi/∂ci>0,由c1≥c2≥c3,可得h1≥h2≥h3。 性质2:μp(h1)≥μp(h2)≥μp(h3)。 证明:最小VaR和最小CVaR对冲组合收益率的均值之差为: (9) 同理可证: (10) (11) 证明:最小VaR和最小CVaR对冲组合收益率的方差之差为: (12) 同理可证: (13) (14) 综上可得,最小VaR对冲组合收益率的均值和方差大于最小CVaR对冲组合收益率的均值和方差,最小CVaR对冲组合收益率的均值和方差大于最小方差对冲组合收益率的均值和方差。经济意义:根据优化问题p1,k为投资者赋予波动率的权重,人们在均值收益与波动之间进行权衡。当k较大时,人们赋予波动权重更大,更加关注波动风险,反之,当k较小时,人们赋予波动权重就小,此时人们更关注收益。由k1≤k2≤k3=+∞可知,最小方差赋予波动的权重最大,其只关心波动而不关心收益,最小VaR赋予波动的权重最小,所以优化问题的结果是最小方差策略的波动最小,同时均值收益也最小,最小VaR对冲策略的方差最大,但均值收益也最大,最小CVaR策略介于二者之间。 由性质2和性质3可知,最小VaR对冲策略下的组合收益率具有最大的均值,但同时也具有最大的方差,是一个相对激进的对冲策略。最小方差对冲策略具有最小的方差,但只能获得最小的均值收益,是一个相对保守的策略。最小CVaR对冲策略居二者之间。所以仅比较均值收益和波动风险,无法判断哪个对冲策略更优。以下引入期望效用理论(Expected Utility Theory, EUT)对这三种策略的对冲效率进行分析。 3.1 风险中性效用函数 定义在随机收益x上的风险中性效用函数U(·)可表示为: U(x)=mx+n, (m>0) (15) 其中m,n为常数,那么风险中性投资者在对冲组合收益率上的效用为: U(rp(h))=mrp(h)+n, (m>0) (16) 根据性质2,容易得到: (17) 所以综上,可得结论1: E[U(rp(h1))]≥E[U(rp(h2))]≥E[U(rp(h3))] (18) 上式等号仅在μ2=0,ρ=±1或α=0三种特殊情况下成立。但在一般情况下,上式说明:风险中性投资者在最小VaR对冲策略上得到的期望效用最高,在最小方差对冲策略上得到的期望效用最低,在最小CVaR对冲策略上得到的期望效用居中,所以风险中性投资者更偏好最小VaR对冲策略。 3.2 二次效用函数 定义在随机收益x上的二次效用函数U(·)可表示为: U(x)=-ax2+bx+c (19) 其中,a,b,c为常数且a>0,b>0。二次效用函数常用于金融资产定价和投资组合选择问题的研究,在正态分布下,基于二次效用函数的投资组合选择与均值-方差模型是一致的。为了将风险厌恶程度与对冲策略选择联系起来,以下引入风险厌恶系数,风险厌恶系数分为绝对风险厌恶系数和相对风险厌恶系数,二者都可以刻画投资者的风险厌恶程度。二次效用函数的绝对风险厌恶系数为: (20) 其中,β=b/2a,绝对风险厌恶系数γ值越大,人们越厌恶风险。由(20)式可知,绝对风险厌恶系数γ与β负相关,β增大时,绝对风险厌恶系数减小。 对于具有二次效用函数的投资者来说,其在对冲组合收益率上的效用为: U(rp(h))=-a(rp(h))2+b(rp(h))+c (21) 此效用依赖于对冲比率h,上式对h求一阶导可得: (22) (22)式两边对h求导,可得: (23) 根据(23)式,容易验证,当k>2时,∂kU(rp(h))/∂kh=0。所以此时,效用函数U(·)在h0处的泰勒展开式可写为: (24) 上式两边取期望并简单变形可得: (25) 所以根据(25)式和c1≥c2≥c3=0的条件,可得: ①最小VaR对冲策略与最小CVaR对冲策略在对冲组合收益率上的期望效用之差为: (26) 令E[U(rp(h1))]-E[U(rp(h2))]=0,经过一系列推导可得: (27) 当β∈(0,β1)时,E[U(rp(h1))] ②最小VaR对冲策略与最小方差对冲策略在对冲组合收益率上的期望效用之差为: (28) 令E[U(rp(h1))]-E[U(rp(h3))]=0,可得: (29) 当β∈(0,β2)时,E[U(rp(h1))] ③最小CVaR对冲策略与最小方差对冲策略在对冲组合收益率上的期望效用之差为: (30) 令E[U(rp(h2))]-E[U(rp(h3))]=0,可得: (31) 当β∈(0,β3)时,E[U(rp(h2))] 由c1≥c2≥c3=0,对比(27)、(29)和(31)式,易得β1≥β2≥β3。所以综上,可得结论2: 当β∈(0,β3)时,E[U(rp(h1))]≤E[U(rp(h2))]≤E[U(rp(h3))]; 当β∈[β3,β2)时,E[U(rp(h1))]≤E[U(rp(h3))]≤E[U(rp(h2))]; 当β∈[β2,β1)时,E[U(rp(h3))]≤E[U(rp(h1))]≤E[U(rp(h2))]; 当β∈[β1,+∞)时,E[U(rp(h3))]≤E[U(rp(h2))]≤E[U(rp(h1))]。 在二次效用函数下,β越小,γ越大,人们的风险厌恶程度越高,人们更偏好最小方差对冲策略h3;反之,当β越大时,γ就越小,人们的风险厌恶程度越低,此时人们更偏好最小VaR对冲策略h1。当风险厌恶程度处于中间时,人们最偏好最小CVaR对冲策略h2。所以可得,在二次效用函数下,风险厌恶程度小的投资者更偏好最小VaR对冲策略,只有那些极端风险厌恶的投资者才偏好最小方差对冲策略。这再次说明最小方差策略最为保守。 3.3 CARA效用函数 定义在随机收益x上的CARA效用函数U(·)可表示为: U(x)=-e-δx,(δ>0) (32) 由U′(x)=δe-δx,U″(x)=-δ2e-δx,可得绝对风险厌恶系数: γ=-U″(x)/U′(x)=δ (33) δ越大,人们越风险厌恶,相反,δ越小,人们风险厌恶程度越低。根据正态分布随机变量的矩生成函数,可得CARA效用函数下的期望效用为: (34) 根据(34)式,可得: ①最小VaR对冲策略与最小CVaR对冲策略在对冲组合收益率上的期望效用之比为: (35) (36) 不难发现: 当δ∈(0,δ1)时,E[U(rp(h1))]>E[U(rp(h2))];当δ∈[δ1,+∞)时,E[U(rp(h1))]≤E[U(rp(h2))]。 ②最小VaR对冲策略与最小方差对冲策略在对冲组合收益率上的期望效用之比为: (37) (38) 同理,不难发现: 当δ∈(0,δ2)时,E[U(rp(h1))]>E[U(rp(h3))];当δ∈[δ2,+∞)时,E[U(rp(h1))]≤E[U(rp(h3))]。 ③最小CVaR对冲策略与最小方差对冲策略在对冲组合收益率上的期望效用之比为: (39) (40) 同理,不难发现: 当δ∈(0,δ3)时,E[U(rp(h2))]>E[U(rp(h3))];当δ∈[δ3,+∞)时,E[U(rp(h2))]≤E[U(rp(h3))]。 由c1≥c2≥c3=0,对比(36)、(38)和(40)式,易得δ1≤δ2≤δ3。所以综上,可得结论3: 当δ∈(0,δ1)时,E[U(rp(h1))]≥E[U(rp(h2))]≥E[U(rp(h3))]; 当δ∈[δ1,δ2)时,E[U(rp(h2))]≥E[U(rp(h1))]≥E[U(rp(h3))]; 当δ∈[δ2,δ3)时,E[U(rp(h2))]≥E[U(rp(h3))]≥E[U(rp(h1))]; 当δ∈[δ3,+∞)时,E[U(rp(h3))]≥E[U(rp(h2))]≥E[U(rp(h1))]。 当绝对风险厌恶系数δ小时,人们风险厌恶程度小,人们更偏好最小VaR对冲策略h1;当绝对风险厌恶系数δ大时,人们的风险厌恶程度大,此时人们更偏好最小方差对冲策略h3;介于中间时,人们更偏好最小CVaR对冲策略h2。 综上可知,最小方差对冲策略只考虑收益率的方差,不关心均值,而最小VaR对冲策略不仅考虑方差,同时考虑均值。对于那些风险厌恶水平较低和风险中性的投资者而言,他们权衡均值带来的平均收益和方差带来的波动风险,他们愿意承担更高程度的波动风险而为此获得更高的均值收益(相对于最小方差策略),因此他们往往更偏好最小VaR对冲策略。而最小CVaR对冲策略介于二者之间。风险厌恶程度不是特别高也不是特别低的投资者偏好最小CVaR对冲策略。 表1 算例一的计算结果 算例一。为了直观上理解以上的理论发现,下面给出一个算例分析。假设市场上存在某种现货产品,其收益率的均值和标准差取值分别为μ1=0.3,σ1=0.4,其对应的期货产品收益率的均值和标准差分别为μ2=0.2,σ2=0.2,相关系数ρ=0.6。取损失概率α=1%,2%,…,10%,根据前面公式,代入数值进行计算,结果见表1。 ①风险中性效用函数下的期望效用 n的取值不影响比较结果,故不妨令n=0,由(16)式可得,三种对冲策略的期望效用为: 图1 风险中性效用函数下的期望效用 图2 二次效用函数下的期望效用 图1直观地显示期望效用随参数m的变化趋势,无论m取何值,都有U1>U2>U3,即在风险中性效用函数下,最小VaR对冲策略的期望效用最高,而最小方差策略的期望效用最低,最小CVaR居中,符合理论预期,验证了结论1。 ②二次效用函数下的期望效用 取a=1,c=0,则b=2β,由(21)式可得,三种对冲策略的期望效用分别为: 图2显示三种对冲策略的期望效用随β的变化趋势,及β1=0.482 β2=0.305 β3=0.237三条直线,由图象可知,U1,U2确实在β1=0.482处相交,U1,U3确实在β2=0.305处相交,U2,U3确实在β3=0.237处相交。另外可知,当0<β<β3时,U3>U2>U1;当β3≤β<β2时,U2>U3>U1;当β2≤β<β1时,U2>U1>U3;当β≥β1时,U1>U2>U3。验证了结论2。 ③CARA效用函数下的期望效用 由(34)式可得,三种对冲策略在CARA效用函数下的期望效用分别为: 图3显示了三种期望效用随风险厌恶系数δ的变化趋势,第一幅图显示U1,U2在δ1处相交,第二幅图显示U1,U3在δ2处相交,第三幅图显示U2,U3在δ3处相交。同理可得,算例结果与结论3是一致的。 算例二。为了进一步检验本文理论结果在实践中的应用价值,我们选取了沪深300股票指数及其期货进行实证分析。数据选取区间为2010年5月至2014年9月共计53个月度的历史数据。金融时间序列数据通常分为高频数据和低频数据,高频数据(日数据或者分钟数据)一般具有尖峰厚尾等非正态分布特征,而低频数据(月度、季度或者年度数据)通常更接近正态分布。为了验证本文正态分布下的理论结果,所以我们选择月度数据。同时由于沪深300股指期货于2010年4月16日正式上市,鉴于上市之初市场噪音较大,而且第一个月交易时间不足一个月。所以我们剔除了2010年4月的数据。数据的描述性统计见表2。 由表2,从均值(Mean)来看,沪深300现货与期货价格在样本期间平均来说是下降的;从中位数(Med)来看,收益率为负的天数大于收益率为正的天数;从最小值(Min)、 最大值(Max)和方差(Var) 图3 CARA效用函数下的期望效用 表2 沪深300股指及其期货收益率的描述性统计 表3 基于沪深300股票指数与股指期货的实证结果 来看,期货收益率的波动要大于现货;从偏度系数(Skewness)、峰度系数(Kurtosis)、JB统计量和P值来看,不能拒绝现货收益率和期货收益率服从正态分布的假设。故可以运用本文在正态假设下的理论进行分析,将相关数据代入公式可得如下的实证结果(见表3)。表3的分析结果与表1相同,在此不再赘述。同时,期望效用下的表现也与算例1类似,限于篇幅,相关图形不再列出。 与传统的对冲效率仅比较风险下降比率不同,本文从期望效用视角对对冲效率进行了比较和分析。我们借助金融经济学上常用的风险中性效用函数、二次效用函数和CARA效用函数比较最小方差、最小VaR和最小CVaR对冲策略的期望效用,从而把人们的风险态度同对冲策略选择联系起来。本文得到的基本结论是:三种对冲策略中,最小VaR对冲策略最为激进,具有最大均值和方差;最小方差对冲策略最为保守,具有最小的均值和方差;最小CVaR对冲策略介于二者之间。风险中性投资者和风险厌恶程度低的投资者更偏好最小VaR对冲策略;风险厌恶程度高的投资者更偏好最小方差对冲策略;风险厌恶程度介于中间的投资者更偏好最小CVaR对冲策略,从而实现了不同风险态度的投资者选择不同的风险对冲策略的目的。 [1] Chen S S, Lee C, Shrestha K. Futures hedge ratios: A review[J]. The Quarterly Review of Economics and Finance, 2003, 43(3): 433-465. [2] 彭红枫, 陈奕. 中国铜期货市场最优套期保值比率估计——基于马尔科夫区制转移GARCH模型[J]. 中国管理科学, 2015, 23(5): 14-22. [3] 付剑茹, 张宗成. 时变最优套期保值比估计及比较研究—基于卡尔曼滤波在状态空间模型中的应用[J].管理科学学报, 2010, 13(12): 23-33. [4] 王辉, 孙志凌, 谢幽篁. 中国农产品期货套期保值非对称效应研究[J]. 统计研究, 2012,(7): 68-74. [5] Lien D, Luo Xiangdong. Estimating the extended mean-gini coefficient for futures hedging[J]. Journal of Futures Markets, 1993, 13(6): 665-676. [6] Shalit H. Mean-Gini hedging in futures markets[J]. Journal of Futures Markets, 1995, 15(6): 617-635. [7] Chen S S, Lee C F, Shrestha K. On amean-generalized semivariance approach to determining the hedge ratio[J]. Journal of Futures Markets, 2001, 21(6): 581-598. [8] Harris R D F, Shen J. Hedging and value at risk[J]. Journal of Futures Markets, 2006, 26(4): 369-390. [9] Cao Zhiguang, Harris R D F, Shen Jian. Hedging and value at risk: A semi-parametric approach[J]. Journal of Futures Markets, 2010, 30(8): 780-794. [10] 迟国泰, 赵光军, 杨中原. 基于CVaR的期货最优套期保值比率模型及应用[J]. 系统管理学报, 2009, 18(1): 27-33. [11] 黄金波, 李仲飞, 周先波. VaR与CVaR的敏感性凸性及其核估计[J]. 中国管理科学, 2014, 22(8): 1-9. [12] 黄金波, 李仲飞, 姚海祥. 基于CVaR核估计量的风险管理[J]. 管理科学学报, 2014, 17(3): 50-60. [13] Chen Yiting, Ho K Y, Tzeng L Y. Riskiness-minimizing spot-futures hedge ratio[J]. Journal of Banking & Finance, 2014, 40: 154-164. [14] Kolb R W, Okunev J. Utility maximizing hedge ratios in the extended mean Gini framework[J]. Journal of Futures Markets, 1993, 13(6): 597-609. [15] Hsln C W, Kuo J, Lee C F. A new measure to compare the hedging effectiveness of foreign currency futures versus options[J]. Journal of Futures Markets, 1994, 14(6): 685-707. [16] 姚海祥, 李仲飞. 基于非参数估计框架的期望效用最大化最优投资组合[J]. 中国管理科学, 2014, 22(1): 1-9. [17] Markowitz H. Portfolio selection[J]. Journal of Finance, 1952, 7(1):77-91. [18] Rockafellar R T, Uryasev S. Conditional value-at-risk for general loss distributions[J]. Journal of Banking & Finance, 2002, 26(7): 1443-1471. [19] Jorion P. Value at risk: The new benchmark for managing financial risk[M].New York: McGraw-Hill, 2007. [20] 刘俊山. 基于风险测度理论的VaR与CVaR的比较研究[J]. 数量经济技术经济研究, 2007, 24(3): 125-133. [21] Yao Haixiang, Li Yong, Benson K. A smooth non-parametric estimation framework for safety-first portfolio optimization[J]. Quantitative Finance, 2014, 15(11): 1-20. [22] Yao Haixiang, Li Zhongfei, Lai Yongzeng. Mean-CVaR portfolio selection: A nonparametric estimation framework[J]. Computers & Operations Research, 2013, 40(4): 1014-1022. [23] 刘静, 杨善朝, 姚永源. α-混合序列下期望损失ES的两步核估计[J]. 应用概率统计, 2010, 26(5): 485-500. Risk Hedging Efficiency in the Perspective of Expected Utility HUANG Jin-bo1, LI Zhong-fei2, ZHOU Hong-tao1 (1.School of Finance, Guangdong University of Finance & Economics, Guangzhou 510320, China;2.Sun Yat-Sen Business School, Sun Yat-Sen Universtiy, Guangzhou 510275, China) There are two distinct research frameworks for hedging issues all the time: risk-minimizing models and utility-maximizing models. Risk-minimizing models implicitly assume that people are fully risk averters who only are concerned about the risk and do not care about returns, while utility-maximizing models are constructed to maximize utility functions which include return-risk tradeoff and have to give a weighing parameter for the return and risk usually. There exist certain disadvantages in the two kinds of models above. The former models' shortage is that they doesn't consider the people's subjective risk attitudes (or implying complete risk aversion). The latter models' shortage is that there is not scientific standard to determine the weighing parameter and the utility function setting is very subjective. In addition, the traditional literatures only define risk reducing ratio as the risk hedging efficiency index, but different risk measure indices often induce inconsistent or even contradictory results. Therefore a hedging efficiency index which is independent of risk measure indices is needed.Method: To repair the shortcomings above and absorb the advantages of the two kind of models respectively, firstly hedging strategies based on risk-minimizing models are gotten, then the expected utility theory is applied to compare the hedging efficiency of hedging strategies, so that individual's risk attitude can be linked to hedging strategy choice. The difference with the traditional risk-minimizing model is that we the risk reducing ratio isn't used as hedging efficiency index, while compared with the traditional utility-maximizing model, our method doesn't need to accurately set the weighing parameter.Data:Two cases are designed to test the theorem above. The data of case 1 is generated by simulation method. In case 2, the historical data of CSI 300 stock index and its futures is applied. The data window ranges from May 2010 to September 2014, a total of 53 monthly historical data. The CSI 300 index futures officially are listed on April 16, 2010, because of the very bigger noise at the listed beginning and less than a month trading time in the first month, so the data in April 2010 is removed.Results: Using the risk neutral, quadratic and CARA utility functions, it's strictly proved that the minimum variance hedging strategy is too conservative, and minimum VaR hedging strategy is the most radical. The investors with bigger degree of risk aversion prefer minimum variance hedging strategy, while the investors with risk neutrality or smaller degree of risk aversion prefer minimum VaR strategy. The minimum CVaR hedging strategy is not conservative or radical but moderate.Future research: This paper aims to provide a research framework which studies hedging efficiency under expected utility theory, the research framework has good applicability, openness and can be easily applied to hedging efficiency problem of other derivatives or other risk measure indices. So a new research perspective for other scholar's related research is provided in this paper. risk hedging; expected utility; risk attitude; value-at-risk; conditional value-at-risk 1003-207(2016)03-0009-09 10.16381/j.cnki.issn1003-207x.2016.03.002 2015-06-10; 2015-10-14 国家自然科学基金资助项目(71231008, 71371199, 71502041);中国博士后科学基金资助项目(2014M562246);广东省自然科学基金资助项目(2015A030313629);广州市哲学社会科学“十二五”规划项目(15Q20) 简介:李仲飞(1963-),男(汉族),内蒙古鄂尔多斯人,中山大学管理学院教授,博士生导师,长江学者,博士,研究方向:金融工程与风险管理,E-mail: lnslzf@mail.sysu.edu.cn. F830.9 A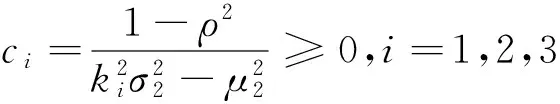

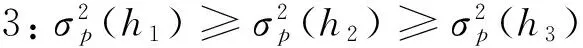
3 期望效用视角下的对冲效率比较
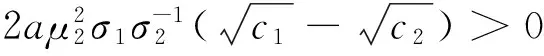
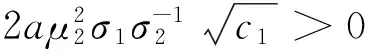
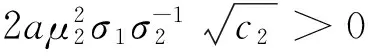



4 算例分析
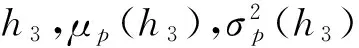



5 结语
