两种分成契约下供应链企业合作减排决策机制研究
2016-12-27李友东谢鑫鹏
李友东,谢鑫鹏,营 刚
(1.内蒙古大学经济管理学院,内蒙古 呼和浩特 010021;2. 军事交通学院,天津 300161)
两种分成契约下供应链企业合作减排决策机制研究
李友东1,谢鑫鹏2,营 刚1
(1.内蒙古大学经济管理学院,内蒙古 呼和浩特 010021;2. 军事交通学院,天津 300161)
本文考虑由一个受政府碳排放规制且处于供应链上游的产品供应商和处于下游的零售商所组成的低碳供应链系统。由于低碳消费需求增加所引起的零售商利润的提高,下游零售商可采取不同的契约形式促进上游供应商扩大减排投资。为此,本文考虑了分享减排所增收益与分担减排投资成本两种契约。通过建立零供两主体的Stackelberg博弈模型,得出了在两种契约下主体的最优减排水平及最优分成比例,以及两主体在不同契约形式下的最优利润值。结果表明:分担减排投资成本契约能够使减排更加彻底,得到的减排水平较高;在分担减排投资成本契约下,两主体的利润值均会有所提高;在分享减排所增利润契约下,两主体的利润变化要依据参数来确定。最后,文章依据合理数据对上述结论进行了验证,并对碳交易价格等相关参数的敏感性进行了分析。
碳规制及交易;减排水平;增值分享契约;成本分担契约;分成比例
1 引言
从1997年的京都议定书到2012年的多哈国际气候大会,国际社会开始更多的关注对人类造成负面影响的全球气候变化问题。资源的过度使用迫使人类为进一步的扩大再生产付出了巨大的代价。最有效的解决方式就是将生产所造成的外部成本内部化,这种方式可以限制人类对环境的破坏并最终实现经济与环境的协调发展。欧盟于2005年制定的“排放交易方案”(Emissions-Trading Scheme, ETS)是碳交易机制的一种尝试[1]。政府实施碳总量控制与排放交易迫使企业选择减排策略,而碳排放权交易的存在,改变了传统企业的成本结构和盈利模式。同时,减排投资决策需考虑减排成本、碳排放权交易后的收益及需求受减排因素影响所带来的收益增加三者之间的权衡[2]。因此在碳排放约束下,研究供应链低碳化运营尤其是供应链低碳化契约设计是目前最重要的热点问题之一。
在考虑市场需求受产品碳排放因素影响的研究中,Wang Fan[3]认为在进行低碳供应链的需求预测时,不仅要以价格作为标准进行判断,还要考虑到在供应链中每个环节的产品碳排放量的大小。Laroche等[4]的研究表明,随着消费者环保意识的增强,越来越多的消费者愿意为环保产品支付更高的价格。Liu Zugang[5]研究了消费者环境意识对供应链上下游企业利润的影响。Plambeck[6]通过实证研究也证实,公司自愿披露产品相关的环境信息,诸如碳排放量等信息,能增加产品的市场份额和消费者的信任。因此当其它条件不变时,产品的市场需求应该与其碳排放量成正相关。关于碳排放权配额分配方面的研究,大多数学者认为碳排放权分配方式主要有免费分配、公开拍卖和标价出售,而前两种方式最为常见[7]。杜少甫等[8]认为企业获得的排放许可来源于三种方式:政府免费分配量,碳市场交易量和碳排放减少量。并且企业做生成决策时会在三者之间权衡以寻求最优利润。本文在建立碳交易模型时也借鉴了上述三种排放权获得的方式,认为企业生产的所有碳排放权来源于政府分配、碳交易以及减排量三个方面。在上述碳分配及交易背景下,一些学者开始讨论碳政策对企业及供应链运营的影响。Sunar等[9]。研究在联合生产中如何将碳排放量分配到生产流程的各个环节。Hua Guowei[10]借助EOQ模型,考虑存在碳排放权交易机制时企业的最优订货批量问题。谢鑫鹏等[11]基于清洁发展机制对供应链低碳化决策及碳交易进行了研究。随后,王芹鹏等[12]运用微分博弈理论,对不合作、成本分担及合作三个契约进行了比较研究。针对供应链的研究主要集中在合作减排上,Poyago-Theotoky[13]考虑了企业减排投资过程中的技术合作问题。Benjaafar等[14]研究如何通过供应链企业合作降低成本及碳排放的问题。Keskin等[15]研究在联合生产中如何将碳排放量分配到生产流程的各个环节。Caro等[16]研究了集中决策和分散决策时供应链的联合减排问题。可以看出:企业合作情况下能够促进减排并降低减排成本。本文将基于减排过程中的实际问题设计两种不同的契约形式并给出相应的结论。
2 问题描述及参数假设
本文考虑由上游减排供应商和下游零售商所组成的低碳供应链系统。在其它条件不变的情况下,供应商的减排会增加消费者对低碳产品的偏好,进而加大了对低碳产品的需求。产品的低碳程度越高,消费者的需求越大;反之越小。不妨设低碳产品的需求Q为产品价格的减函数和减排程度的线性增函数,即为Q=N-b·p+a·τ。其中N为市场容量,p为产品价格,并假设p在减排前后没有发生变化,τ为表征减排程度高低的量,是供应商的决策变量,在本文将其命名为减排水平。
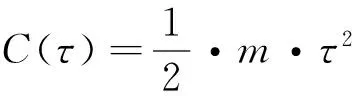
(1)
假设供应商所生产的单位产品的初始碳排放量为es,政府分配给单位产品的碳配额为ds。考虑到政府碳配额的初始分配以及在碳市场中的交易量,供应商所需的总的碳配额将来源于三种渠道:政府分配给所生产产品的初始碳配额ds·Q(假设政府按照单位产品分配碳配额)、总的碳减排量τ·es·Q以及在碳交易市场的交易量Etrading。同时,供应商最终的碳排放数量将不会超过总的碳配额。
为了寻求总利润的最大化,如果供应商实际的碳排放小于政府初始分配的碳配额,它将卖掉多余的量来获取利润;但如果生产所需的碳配额不够,它将会去碳市场购买所需的配额。因此,供应商将充分利用碳配额这种新型的资源。将上述三种渠道所获取碳配额加总可得到下式:
上式经变换,可得碳配额交易量如式(2)所示:
Etrading=es·Q-ds·Q-τ·es·Q
(2)
将式(2)代入式(1),可得:
为了简化下面的计算过程,可令Υ=es·pc,Ψ=(es-ds)·pc,因此供应商的利润函数改为式(3):
(3)
由于零售商不存在减排的问题,因此它的利润函数为:
Πr(e)=(p-w)·Q=(p-w)·(N-b·p+a·τ)
(4)
对于零售商来说,产品的价格是常量,其利润的大小主要取决于上游供应商的减排水平τ。减排水平越高,零售商的利润越多,即零售商利润函数是产品减排水平的单调递增函数。因此,当零售商不向供应商提供任何契约时,可以得到能使供应商取得最大利润的最优减排水平τ*。求供应商利润函数对减排水平的一阶导数,得到:

(5)
将式(5)分别代入零售商和供应商的利润函数中,可得:
Πr(e)*(τ*)=(p-w)·{(N-b·p)·(m-a·Υ)+a2·[w-(c+Ψ)]/m-2a·Υ}
(6)
Πs(e)*(τ*)=Υ2·(N-b·p)2+a2·[w-(c+Ψ)]2+2(m-a·Υ)·(N-b·p)·[w-(c+Ψ)]/2(m-2a·Υ)
(7)

3 模型建立及求解分析
本文考虑主导零售商为了进一步提高由于减排而增加的利润值可以向供应商提供两种契约。其一就是将减排后所增加的利润部分分给供应商,自己享有剩下的部分利润;其二是在减排前分担供应商的减排成本,成本的分担会促进供应商减排的积极性,进而提高减排水平。
3.1 分享减排所增利润契约
此时零售商将低碳产品需求增加部分所获得的增值利润按1-φ的百分比分给上游的减排供应商,用以促使其加大减排投资,进而提高销售收入,而自己只获得增值利润φ的部分。那么,在这种契约形式下零售商和供应商的利润函数分别为:
Πr(e)(φ)=(p-w)·(N-b·p+φ·a·τ)
(8)
(9)
考虑到供应链系统中,零售商首先提出契约,决定增值利润的分享比例φ,然后供应商再根据利润分享比例的大小决策所生产产品的减排水平τ。根据逆向归纳求解法,求供应商利润函数对减排水平的一阶导数,可得:

(10)
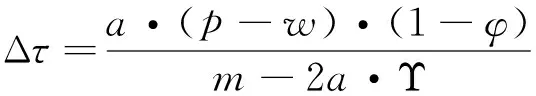
将式(10)代入式(8)中,可得零售商的利润函数为:

(11)
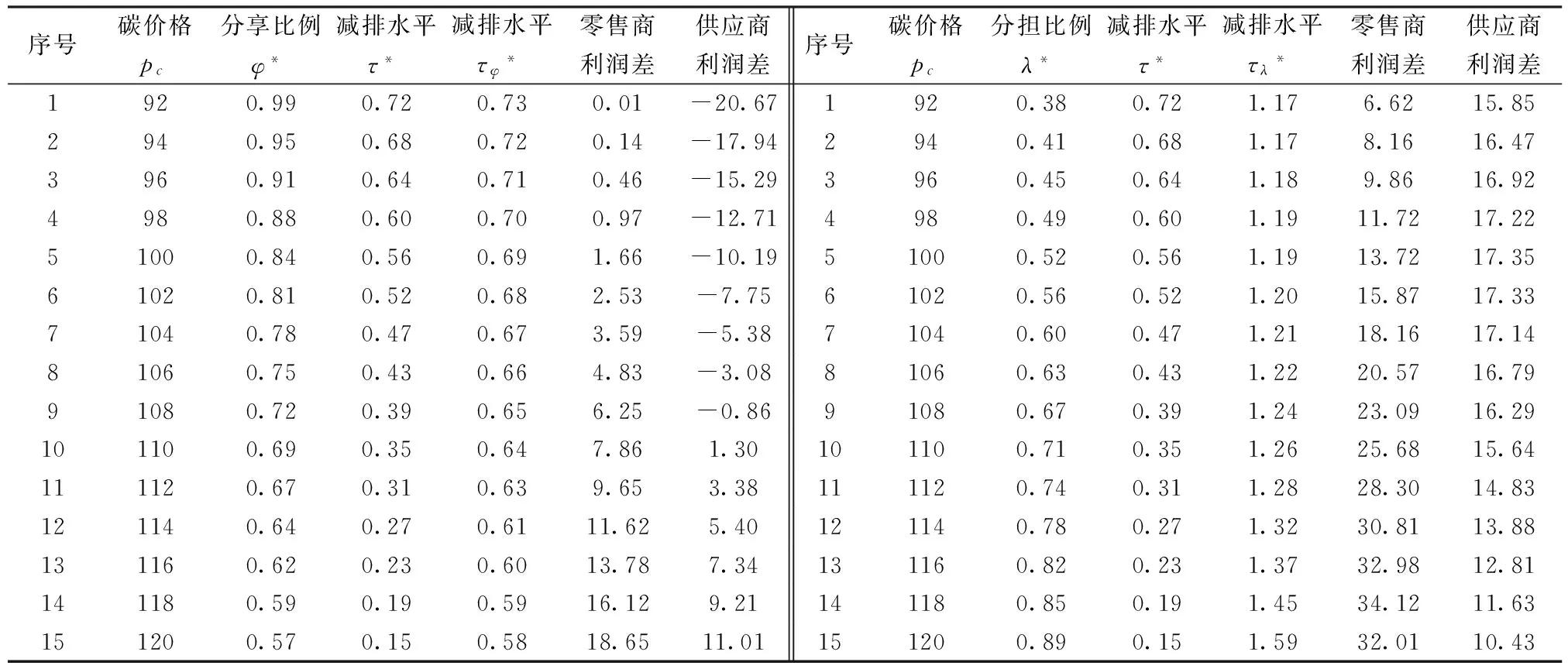
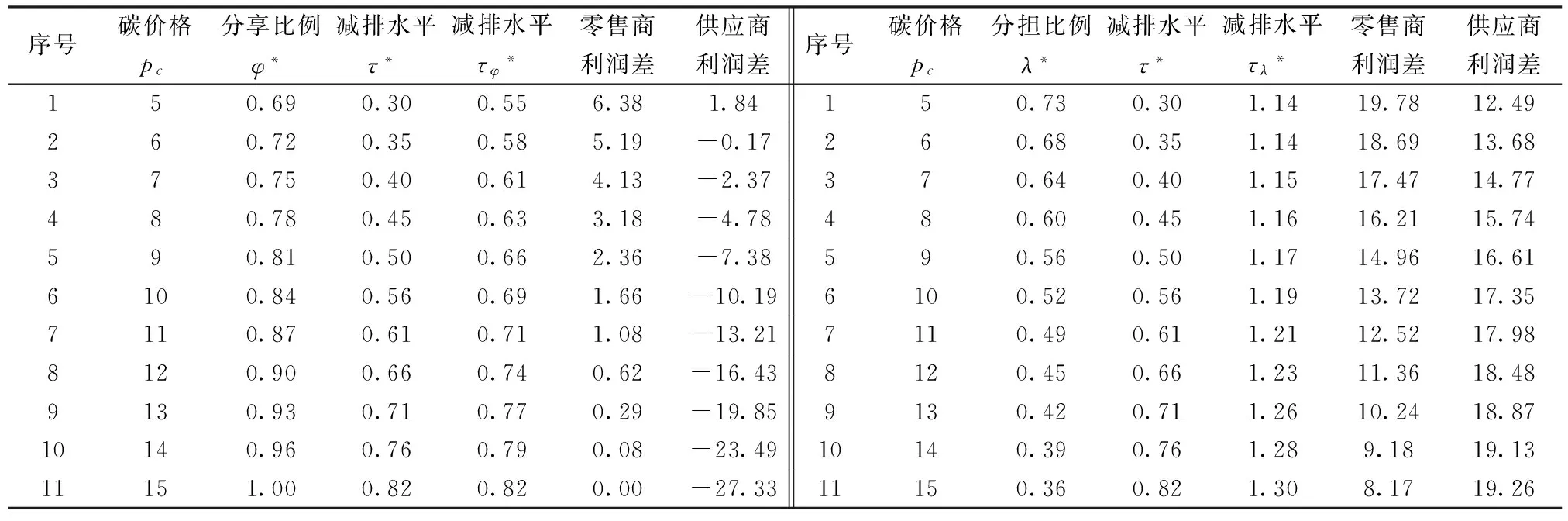
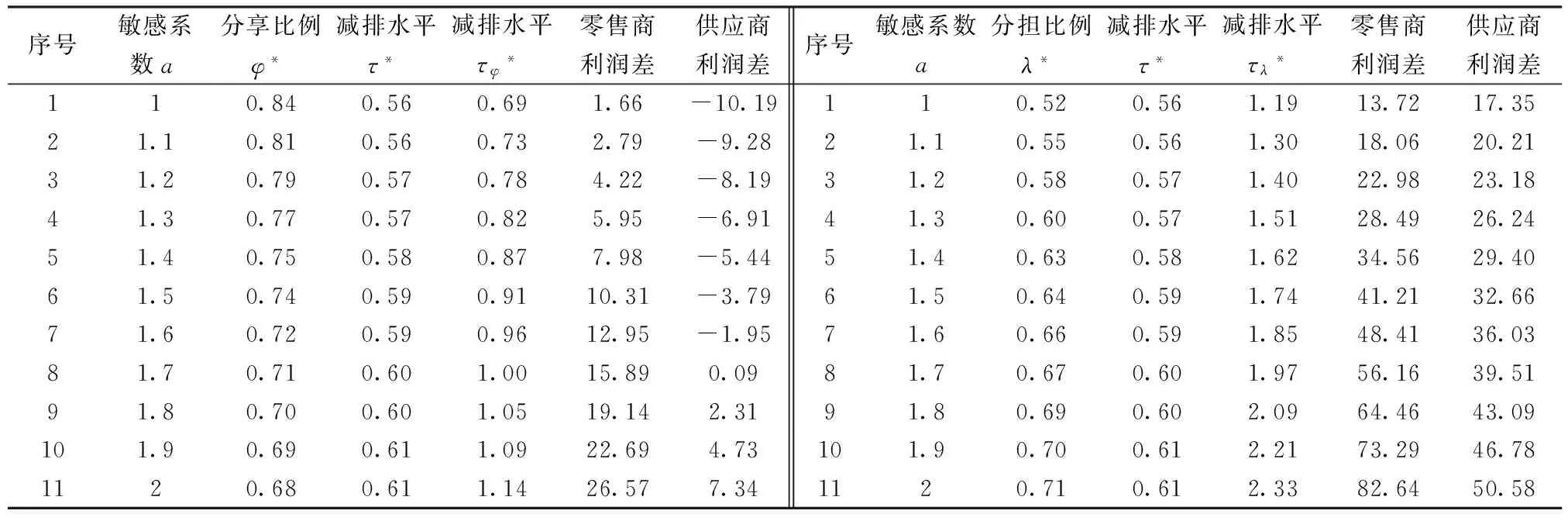
由于分享比例满足0<φ*<1的条件,因此根据式(11)应该有Υ·(N-b·p)+a·[w-(c+Ψ)] 将式(11)代入式(10)可得最优减排水平为: τφ*=τ*+a·(p-w)-Υ·(N-b·p)-a·[w-(c+Ψ)]/2(m-2a·Υ) (12) (13) 3.2 分担减排投资成本契约 该契约下,零售商分担供应商的部分减排成本。假设零售商分担供应商减排成本的百分比为λ,那么供应商只承担1-λ的减排成本,因此零供两主体的利润函数分别为: (14) (15) (16) 求上式对分担比例λ的一阶导数得到: (17) 从式(17)可以看出:由于m-2a·Υ 2a·(p-w)-{Υ·(N-b·p)+a·[w-(c+Ψ)]}<2a·(p-w)+{Υ·(N-b·p)+a·[w-(c+Ψ)]},因此最优分担比例λ*满足0<λ*<1。 将最优分担比例λ*代入式(16)中,得到在分担减排投资成本契约下供应商的最优减排水平为: τλ*=2a·(p-w)+Υ·(N-b·p)+a·[w-(c+Ψ)]/2(m-2a·Υ) (18) 比较分担前的减排水平可以看出:τλ*=τ*+2a·(p-w)-Υ·(N-b·p)-a·[w-(c+Ψ)]/2(m-2a·Υ)。由于a·(p-w)>Υ·(N-b·p)+a·[w-(c+Ψ)],因此2a·(p-w)-Υ·(N-b·p)-a·[w-(c+Ψ)]/2(m-2a·Υ)>0。 结论2:零售商向供应商提供分担减排投资成本契约后,供应商的最优减排水平也将提高,其增量大小为2a·(p-w)-Υ·(N-b·p)-a·[w-(c+Ψ)]/2(m-2a·Υ),最优减排水平与分享比例λ呈负相关,且其相关比例大于{Υ·(N-b·p)+a·[w-(c+Ψ)]}·m/(m-2a·Υ)2。 令函数Θ=2a·m·(p-w)·(m-2a·Υ)·{2a·(p-w)-{Υ·(N-b·p)+a·[w-(c+Ψ)]}},则可得到两种契约分成比例之间的关系为式(19)所示: (19) 由于前面所得a·(p-w)-{Υ·(N-b·p)+a·[w-(c+Ψ)]}>0,且p>w,因此得到2a·(p-w)-{Υ·(N-b·p)+a·[w-(c+Ψ)]}>0,即Θ>0。 将函数Θ还原可得下式: 2a·m·(p-w)·(m-2a·Υ)·{Υ·(N-b·p)+a·[p-(c+Ψ)]+a·(p-w)}·{2a·(p-w)-{Υ·(N-b·p)+a·[w-(c+Ψ)]}}>Υ·(N-b·p)+a·[p-(c+Ψ)] 这也就是说:若上式成立,则λ*>φ*;反之,λ*<φ*。结合零售商分担减排成本的最优分担比例值λ*,可以得出: λ*>Υ·(N-b·p)+a·[p-(c+Ψ)]/2a·m2·(p-w)·{Υ·(N-b·p)+a·[p-(c+Ψ)]+a·(p-w)}2,该式中若令 Ω=Υ·(N-b·p)+a·[p-(c+Ψ)],Ξ=a·(p-w),则: (20) 3.3 各主体利润值的分析与比较 下面考虑在两种契约下零供两主体的最优利润值。 在分享减排所增利润契约下,将最优值(τφ*,φ*)代入式(8),可得零售商最优利润为: (21) 比较没有分享机制时零售商的利润值为Πr(e)*(τ*)=(p-w)·(N-b·p)+a·(p-w)·{Υ·(N-b·p)+a·[w-(c+Ψ)]}/m-2a·Υ,经简单计算,可以得到利润分享前后零售商的利润差值为: ΔΠr(e)*(τφ*,φ*)={Υ·(N-b·p)+a·[p-(c+Ψ)]}2-4a·(p-w)·{Υ·(N-b·p)+a·[w-(c+Ψ)]}/4(m-2a·Υ),由于 Υ·(N-b·p)+a·[w-(c+Ψ)] ΔΠr(e)*(τφ*,φ*)>{Υ·(N-b·p)+a·[p-(c+Ψ)]}2-4a2·(p-w)2/4(m-2a·Υ)={Υ·(N-b·p)+a·[p-(c+Ψ)]+2a·(p-w)}·{Υ·(N-b·p)+a·[w-(c+Ψ)]-a·(p-w)}/4(m-2a·Υ) 上式中,由于Υ·(N-b·p)+a·[w-(c+Ψ)] 将最优值(τφ*,φ*)代入式(9),并经化简最终可以得到供应商的最优利润为式(22)所示: (22) 比较利润分享前后供应商的最优利润值,可以得到它们之间的差值为: ΔΠs(e)*(τφ*,φ*)={Υ·(N-b·p)-a·[p-(c+Ψ)]}2-4{Υ·(N-b·p)+a·[w-(c+Ψ)]2-4a·Υ·(N-b·p)·[w-(c+Ψ)]/8(m-2a·Υ) (23) 由于前面已经得到在利润分享后,零售商的最优利润可能会增加,也可能会减少。因此当满足4{Υ·(N-b·p)+a·[w-(c+Ψ)]}2-{Υ·(N-b·p)+a·[p-(c+Ψ)]}2>0时,将上式代入式(23)可得: ΔΠs(e)*(τφ*,φ*)={Υ·(N-b·p)-a·[p-(c+Ψ)]}2-4{Υ·(N-b·p)+a·[w-(c+Ψ)]}2-4a·Υ·(N-b·p)·[w-(c+Ψ)]/8(m-2a·Υ)<{Υ·(N-b·p)-a·[p-(c+Ψ)]}2-{Υ·(N-b·p)+a·[p-(c+Ψ)]}2-4a·Υ·(N-b·p)·[w-(c+Ψ)]/8(m-2a·Υ)=-4a·Υ·(N-b·p)·{[p-(c+Ψ)]+[w-(c+Ψ)]}/8(m-2a·Υ)<0 这说明,假若零售商在实行利润分享契约后最优利润值有所减少,那么供应商在该契约下的最优利润值也会减少。 而当满足4{Υ·(N-b·p)+a·[w-(c+Ψ)]}2-{Υ·(N-b·p)+a·[p-(c+Ψ)]}2<0时,不能通过解析式判断供应商利润值的增加或减少。这样就是说,假若零售商在实行利润分享契约后最优利润值有所增加,那么供应商在该契约下的最优利润值可能会增加也可能会减少。 结论4:在分享减排所增利润契约下,假如零售商的利润值降低了,那么供应商的利润值一定也是降低的;而假如零售商的利润值提高了,那么供应商的利润可不一定就会提高。 下面来看减排成本分担情况下零供主体的利润。首先,为了计算简便,令Λ=Υ·(N-b·p)+a·[w-(c+Ψ)],由于前面已设Ξ=a·(p-w),则式(17)可化为式(24): (24) 同样,式(18)可表示为: (25) 将式(24),(25)代入式(14),(15)中,可得在成本分担情况下供应商和零售商的利润分别为: 还原Ξ,Λ,得到供应商和零售商的利润值分别为式(26),(27)所示: Πr(e)*(τλ*,λ*)=(p-w)·(N-b·p)+{a·(p-w)+Υ·(N-b·p)+a·[p-(c+Ψ)]}2/8(m-2a·Υ) (26) Πs(e)*(τλ*,λ*)=[w-(c+Ψ)]·(N-b·p)+{Υ·(N-b·p)+a·[w-(c+Ψ)]}·{a·(p-w)+Υ·(N-b·p)+a·[p-(c+Ψ)]}/4(m-2a·Υ) (27) 比较在实施分担成本契约前零售商的利润可以看出: ΔΠr(e)*(τλ*,λ*)=(Ξ-Ω)2-4Ξ·Λ+2Ξ·(Ω-Λ)/8(m-2a·Υ) 由于(Ξ-Ω)2-4Ξ·Λ+2Ξ·(Ω-Λ)=(Ω-Ξ)·(Ω+Ξ)-4Ξ·Λ+2Ξ·(Ω-Λ)>4Ξ·(Ω+Ξ)-4Ξ·Λ=4Ξ·(Ω+Ξ-Λ)>4Ξ·Ω>0,因此说明实行减排成本分担契约后,零售商的利润将会有所增加。 同理,比较实施分担成本契约前供应商的利润可以看出: ΔΠs(e)*(τλ*,λ*)=Λ·(Ξ+Ω)-2(Λ)2+4a·Υ·(N-b·p)·[w-(c+Ψ)]/4(m-2a·Υ) 由于Ξ>Λ且Ω>Λ,因此有Λ·(Ξ+Ω)>Λ·2Λ=2(Λ)2,即ΔΠs(e)*(τλ*,λ*)=Πs(e)*(τλ*,λ*)-Πs(e)*(τ*)>0。这就是说,实行减排成本分担契约后,供应商的利润也会有所增加。 结论5:在分担减排投资成本契约下,供应商和零售商的利润值均会有所提高,其中零售商利润提高值大于a·(p-w)·{Υ·(N-b·p)+a·[p-(c+Ψ)]}/2(m-2a·Υ);供应商利润提高值大于a·Υ·(N-b·p)·[w-(c+Ψ)]/m-2a·Υ。 下面再比较两种契约下各主体的利润情况。首先看零售商的利润函数,由于前面已设Ω=Υ·(N-b·p)+a·[p-(c+Ψ)],因此在分享减排增值利润及分担减排投资成本契约下零售商的利润函数可分别表示为: 结论6:比较两种不同契约下零供两主体的利润函数可以得到,当满足条件a·(p-w)>Υ·(N-b·p)+a·[p-(c+Ψ)]时,基于增值利润分享契约下零售商的利润大于基于成本分担契约下零售商的利润,反之则小于;而对于供应商来说,如果在减排增值利润分享契约下它的利润是减少的,那么减排成本分担契约能够使供应商得利润值增加,如果在减排增值利润分享契约下它的利润是增加的,那么两种契约下供应商利润值的大小要依据具体的参数来判断。 为了能够说明上述问题及其结论并且能够使得计算过程简便,验证过程假设供应商所生产低碳产品的市场容量为N=250,供应商给零售商的产品批发价格为w=20,该产品的零售价格为p=100,产品需求对价格的敏感系数为b=2,供应商减排的努力程度系数为m=100,需求对减排水平的敏感系数为a=1,单位产品的生产成本为c=15,单位产品的碳排放量为es=0.1,政府规制下限定的单位产品的排放上限为ds=0.05,当时的碳交易价格为pc=10。首先通过设定不同的低碳产品的零售价格p,来观察在两种不同契约下零售价格p是如何影响零供两主体利润值的。 从表1可以看出:当选取低碳产品的零售价格p∈[92,120]时,无论是分享利润契约还是分担成本契约,均可提高供应商的减排水平,但是在分担成本契约下,供应商的减排水平更高,从而验证了3.2中推论所得结论。在分享利润契约下,零售商利润较不提供契约时会有所提高,但是供应商的利润值会出现在产品零售价格较低时减少而在产品零售价格较高时增加的现象;而在分担成本契约下,零供两主体利润均会提高,从而验证了3.3中的结论4和5。并且,无论是哪种契约,零售商较不提供契约时的利润差均随产品零售价格的提高而增加,而供应商在分担成本契约下获得的利润增量在零售价格区间内存在峰值。下面再来看最优值随价格敏感系数b的变化关系。 表1 两主体最优值及最优利润随低碳产品零售价格p的变化关系 表2 两主体最优值及最优利润随产品价格敏感系数b的变化关系 表3 两主体最优值及最优利润随碳交易价格pc的变化关系 选取需求价格敏感系数b∈[1.95,2.30],由于价格敏感系数b与产品的零售价格p类似,因此对价格敏感系数b分析的结论也与对零售价格p分析的结论相似。只是供应商在分担成本契约下获得的利润增量随着价格敏感系数b的提高而减少。 选取碳交易价格的变化范围为pc∈[5,15]。从表3可以看出:无论是哪种契约,最优减排水平均会提高,并且在分担成本契约下得到的减排水平更高。但与产品零售价格不同的是,减排水平随着碳交易价格的提高而变大,这主要是由于市场的碳交易价格变高,使得供应商放弃从碳市场购买所需的碳配额,而是考虑加大减排投资力度,从而使得减排水平变大。并且,在两种契约下,零售商的利润均会变大,但零售商更倾向于低的碳交易价格,高的碳交易价格会使其利润增量变得很小;而供应商在分担成本契约下则更希望较高的碳交易价格, 因为高的 表4 两主体最优值及最优利润随碳排放敏感系数a的变化关系 碳价格能使其利润增量变大。这也从一个侧面证实了碳交易价格的波动不仅仅对受政府碳规制的制造型企业产生影响,更重要的波及其所处供应链的上下游企业。 表4说明随着消费市场对低碳产品认知度的提升,两种契约下零售商及供应商都将获利,并且随着低碳敏感系数a的变大,零售商和供应商的利润增量也在变大。因此供应链中各企业通过各种方式来提高消费者对低碳产品的认可度,以扩大低碳产品潜在的市场份额。 本文考虑了由上游受政府碳规制的减排供应商和下游销售其产品的零售商所组成的供应链系统。产品的市场需求是供应商减排水平的增函数,零售商为了扩大需求进而提高销售利润,可以通过两种契约方式激励供应商扩大减排投资额。一种为分享由于减排所增收的利润,另一种为分担减排所付出的成本。通过建立零售商和供应商之间的Stackelberg博弈模型,得出了在上述两种契约下各主体的最优减排水平及最优分成比例,进而得出两主体在不同契约形式下的最优利润值。通过分析比较可以得出:分担减排投资成本契约能够使供应商的减排更加彻底有效,得到的最优减排水平较高;并且在分担减排投资成本契约下,两主体的利润值均会有所提高;而在分享减排所增利润契约下,两主体的利润变化要依据参数来确定。这说明,分担减排成本契约能够更加有效的提高零供两主体的利润,而分享减排所增利润契约不能够较好的促进供应商减排的积极性,只能单方面的对零售商有利。最后,文章依据合理数据对上述结论进行了验证,并对产品价格、碳交易价格及低碳消费需求敏感度等相关参数的敏感性进行了分析和说明。 文中假设低碳产品的零售价格为常量,这对处于供应链主导地位的零售商来说具有一定的限定,在实际中零售商可能会对低碳产品重新定价,但现实中也可能出现低碳环保型产品的价格与普通产品相差不多的情况。因此本文假定产品价格为常量具有一定的代表性,在接下来的研究中会考虑将产品价格作为零售商的决策变量来进行分析,希望能够得出更加有意义的结论和启示。 [1] Ellerman D,Buchner B. The European Union emissions trading scheme: Origins, allocation, and early results[J]. Review of Environmental Economics and Policy, 2007, 1(1): 66-87. [2] Stavins R N. Addressing climate change with a comprehensive US cap-and-trade system[J] Oxford Review of Economic Policy, 2008, 24(2): 298-321. [3] Wang Fan. A multi-objective optimization for green supply chain network design[J], Decision Support Systems 2011, (51) :262-269. [4] Laroche M, Bergeron J, Barbaro-Forleo G. Targeting consumers who are willing to pay more for environmentally-friendly products[J]. Journal of Consumer Marketing, 2001, 18(6): 503-520. [5] Liu Zugang. Consumer environmental awareness and competition in two-stage supply chains[J].European Journal of Operational Research,2012, (218):602-613. [6] Plambeck E L. Reducing greenhouse gas emissions through operations and supply chain management[J]. Energy Economics, 2012, 34(S1): S64-S74. [7] Tietenberg T H, Cui Weiguo. Emissions trading:Reform on pollution control policy[M].Beijing: Beijing Joint Press, 1992. [8] 杜少甫,董骏峰,梁樑,等. 考虑排放许可与交易的生产优化[J].中国管理科学, 2009, 17(3): 81-86. [9] Sunar N, Plambeck E L.Greenhouse gas emissions accounting: Allocating emissions from processes to co-products[R]. Working Paper, Stanford GSB, 2011. [10] Hua Guowei, Cheng T C E, Wang Shouyang. Managing carbon footprints in inventory management[J]. International Journal of Production Economics, 2011, 132(2): 178-185. [11] 谢鑫鹏,赵道致.低碳供应链企业减排合作策略研究[J].管理科学, 2013, 26(3): 108-119. [12] 王芹鹏,赵道致.两级供应链减排与促销的合作策略研究[J].控制与决策, 2014,29(2): 307-314. [13] Poyago-Theotoky J A. The organization of R&D and environmental policy[J].Journal of Economic Behavior & Organization, 2007,62(1):63-75. [14] Benjaafar S, Li Yanzhi,Daskin M.Carbon footprint and the management of supply chains: insights from simple models[J].Transactions on Automation Science and Engineering,2013,10(1):99-116. [15] Keskin N,Plambeck E.Greenhouse gas emissions accounting: Allocating emissions from processes to co-products[R]. Working Paper, Stanford GSB,2011. [16] Caro F, Corbett C, Tan T, et al. Carbon-optimal and carbon-neutral supply chains[R]. Working Paper, Anderson graduate school of management-decisions, operations and technology management, UC Los Angeles, 2011. Research on Supply Chain Collaboration Sharing Contract and Decision-making Mechanism under the Limitation of Carbon Emission LI You-dong1, XIE Xin-peng2, YING Gang1 (1. School of Economics and Management,Inner Mongolia University, Hohhot Inner Mongolia 010021,China;2. Military Traffic Institute, Department of Automotive Engineering, Tianjin 300161,China) In this paper an emission-dependent supply chain system consisting of one single upstream emission-dependent manufacturer and one single downstream retailer is considered. Because its profit increases caused by the increased demand of low carbon consumption, retailer may conduct different contracts in order to promote the emission-dependent supplier to expand reduction investment. Therefore, two kinds of contract, which is called reduction increment income sharing contract and reduction investment cost sharing contract will be designed. Through the establishment of the two agents’ Stackelberg game model, the optimal abatement levels and sharing rates can be obtained under the two different contracts, and two agents’ optimal profits can also be calculated. The results show that reduction investment cost sharing contract can make the emission reduction more thoroughly and the obtained emission level is higher; in the reduction investment cost sharing contract, the two agents’ profit will be increased; but in the reduction increment income sharing contract, the two agents’ profit increments may be determined according to relevant parameters. Finally, based on the reasonable data the conclusions are verified, and the price of carbon emission permit and other related parameters’ sensitivity can be analyzed. carbon emission regulation and trade; emission reduction; reduction income sharing contract; reduction cost sharing contract; sharing rate 1003-207(2016)03-0061-10 10.16381/j.cnki.issn1003-207x.2016.03.008 2014-03-12; 2014-11-19 国家自然科学基金资助项目(71263033);内蒙古自然科学基金资助项目(2015MS0709);内蒙古大学高层次人才科研启动项目(135144) 简介:李友东(1978-),男(汉族),内蒙古呼和浩特市人,内蒙古大学经济管理学院讲师,博士,研究方向:供应链管理与优化、博弈论等,E-mail: nmglyd@163.com. F274 A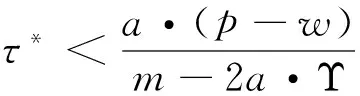
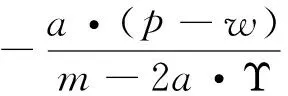
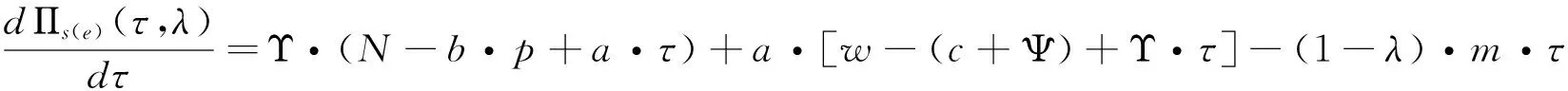
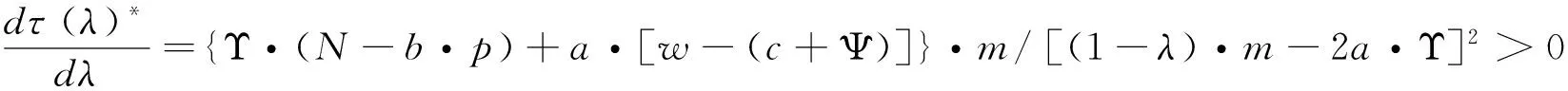
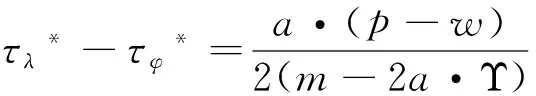
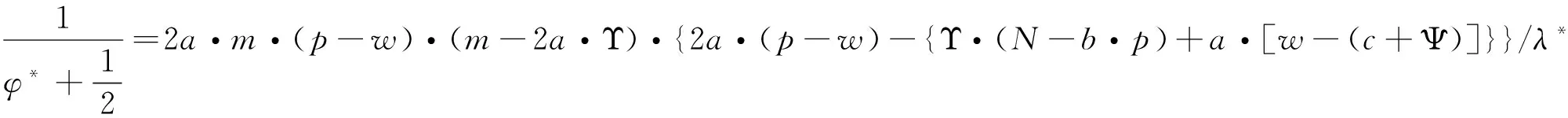
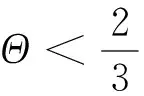

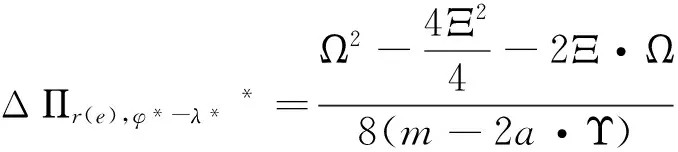
4 数值分析

5 结语
