基于贝叶斯网络d-分隔定理的节点置信度计算方法
2016-12-26亢凯航王云峰
王 辉 亢凯航 王云峰
(河南理工大学计算机科学与技术学院 河南 焦作 454000)
基于贝叶斯网络d-分隔定理的节点置信度计算方法
王 辉 亢凯航 王云峰
(河南理工大学计算机科学与技术学院 河南 焦作 454000)
现有的贝叶斯网络节点置信度计算方法,存在着因条件概率的错误计算和节点的相关性导致的节点置信度错误计算问题。这些问题降低了节点置信度的准确性,影响了网络威胁传播路径预测的有效性。为此,提出基于贝叶斯网络d-分隔定理的节点置信度计算方法。首先,通过分析攻击成本和攻击行为发生的可能性之间的关系,提出攻击行为发生的条件概率计算方法,以解决条件概率的错误计算问题;其次,通过引入贝叶斯网络分隔定理,使存在关联性的节点在它们共有的d-分隔集合条件下相互独立,并提出节点置信度的计算方法,以有效地避免相关性导致的节点置信度错误计算;最后,实验结果表明,该方法有效地解决了节点置信度的错误计算问题,提高了节点置信度的准确性,实现了对网络威胁传播路径的有效预测。
节点置信度 条件概率 相关性 d-分隔 攻击成本
0 引 言
近年来,网络系统的安全性日益受到人们的关注。之所以如此,一个重要的原因是现有的网络安全防御技术或安全措施未能很好地解决网络安全问题[1]。目前成熟的防御技术如防火墙、IDS等,是一种根据预定的解决方案对那些已知的且被检测出的安全威胁进行防范的被动防御技术。而对于一些未知的、能高度规避检测的网络攻击,却没有有效的防御办法。因此,我们需要就目标网络可能遭受到的未知威胁进行主动防范,以便管理人员在损失发生之前控制安全威胁。而防范未知安全威胁的一个重要途径就是预测网络威胁的传播路径。
目前,许多组织和目标都致力于通过主动防御技术分析目标网络的安全威胁。这其中,攻击图和贝叶斯网络是应用最为广泛的网络威胁分析工具。攻击图能够基于系统网络配置和脆弱性信息,展示网络威胁的传播路径[2]。依据节点和边表示的含义的不同,攻击图可以分为状态攻击图和因果关系图[3]。因果关系图用节点表示系统条件(属性)和网络攻击,有向边表示节点间的因果关系。因果关系图具有很好的扩展性,但并不具备处理不确定性关系的能力。而贝叶斯网络用节点和有向弧描述攻击行为和攻击证据的依赖关系,具备处理非确定性关系的能力[4]。同时,其本身是一种因果攻击图[5]。考虑到网络威胁的传播路径具有不确定性,因而将贝叶斯网络作为网络威胁分析的有效方法。但是,这种分析方法需要解决节点概率的量化问题[6]。目前,这种标准化工作的一个较为成熟的成果是通用脆弱点评估系统(CVSS)[7,8]。它的一个主要功能是将与安全威胁有关的因素量化为节点概率,为安全威胁概率的计算提供量化值。
当前,基于贝叶斯网络的安全威胁概率计算,主要基于依赖和条件独立假设,即网络节点只与该节点的父节点存在相关性,而与其他节点相互独立。但在实际的节点概率计算中,却存在着节点之间的相关性所导致的概率错误计算问题。这种问题会对网络威胁传播路径的预测带来影响。图1是一个基于贝叶斯网络预测网络威胁传播路径的示例,其中圆形节点表示目标网络中的资源状态节点,有向弧表示攻击步骤。攻击者就是通过改变一系列资源状态节点的状态来获得目的主机权限。
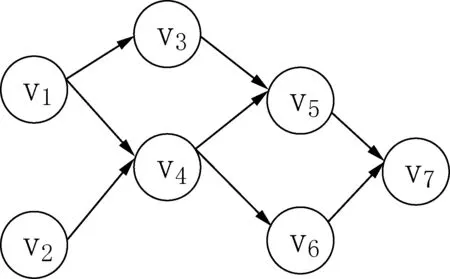
图1 网络威胁传播路径示例
图1中,v7为目标资源状态节点。为了占有v7,攻击者可以沿着两条路径:(1)v1→v4→v5→v7;(2)v1→v4→v6→v7。为了预测网络威胁的传播路径,我们需要计算各节点的概率。这其中,节点v7的概率可以通过计算节点v5和v6的概率得到。在条件独立假设下,我们假设v5和v6是完全独立的,那么节点v7的概率P(v7)为P(v5)+P(v6)-P(v5)·P(v6)。实际上,在P(v4)未确定情况下,P(v5)和P(v6)将呈现出此消彼长的规律,即任一节点发生概率的增大都会相应降低另一节点发生的概率,同时也会影响v7的发生概率。因此,v5和v6、v4和v7存在一定的相关性。这种相关性导致了节点概率P(v7)、P(v5)和P(v6)的错误计算,影响管理人员对网络威胁传播路径的预测。
在具体的网络威胁传播路径场景中,鉴于目标节点的复杂性及重要性不同,攻击者所需付出的成本也不同。因此,成本会成为攻击者选择攻击路径一项重要决策因素。以图1中攻击者以v4为出发点,在节点v5和v6进行抉择为例。我们假设攻击者成功获得节点v5和v6的概率P(v5)>P(v6),成本Cost(v5)>Cost(v6),且Cost(v5)远大于获得节点v5所得收益。此时,攻击者总是倾向于选择节点v6。从成本的角度分析,成本的增加会降低攻击者选择路径v4→v5的可能性,增大选择路径v4→v6的可能性,即减小了条件概率P(v5|v4),增大了条件概率P(v6|v4)。因此,攻击成本能够通过影响条件概率,导致节点置信度的错误计算,影响对网络威胁传播路径的预测。
针对上述问题,本文提出一种预测网络威胁传播路径的方法。这种方法通过引入贝叶斯网络分隔定理,能够回避节点间相关性的影响。通过分析攻击成本对攻击者实施攻击行为的影响,能够解决攻击成本导致的节点置信度错误计算问题,从而,有效地提高网络威胁传播路径预测的准确性。
1 相关研究
网络安全威胁主要通过安全漏洞在目标网络中传播,传播路径具有极大的不确定性。因此,可以通过计算攻击行为发生的可能性和安全漏洞被成功利用的概率预测其传播路径。基于这一思路,文献[6]尝试基于贝叶斯网络和CVSS计算脆弱点被成功利用的概率;Yu等[9]提出了攻击行为发生概率的经验公式,引入了条件概率分析攻击图不同类型节点之间依赖关系;石进等[10]分析了攻击者的成本和收益对节点概率的影响;Mehta等人[11]则认为节点概率的计算,必须考虑攻击图中各个节点具有不同的重要度,并分析了影响重要度的因素。
在具体的网络威胁传播路径场景中,节点间的相关性,以及目标节点的复杂性及重要性的不同,都会导致节点概率的错误计算,影响传播路径的预测,而文献[8-11]则未考虑这点。Homer等[6]提出了导致节点概率的计算出现错误的原因之一是节点之间存在相关性,并基于贝叶斯网络的d-分隔定理,给出了解决这一问题的方法。但是,他没有考虑条件概率对节点概率的影响,且增加节点的方法使得攻击图的理解更加复杂。张少俊等人在文献[12,13]中提出了利用改进的贝叶斯推理似然加权法计算攻击图节点置信度的方法。通过引入攻击证据间的时间偏序关系,简化了节点置信度的计算,在一定程度上提升了其准确性。但是,他只是给出了条件概率的假设值,并未给出计算方法。文献[14]提出隐马尔科夫模型的概率方法消除节点间关联性的影响。方法讨论了成本和收益因素对不同类型节点概率的关联性影响,并通过消除一些关联性较低的节点,提高了节点计算的准确性。但是该方法并未考虑到攻击成本对攻击者的选择策略的影响。吴泓润等人[15]在对网络攻击进行分析时,提出了基于代价下的攻击者选择性攻击策略,试图通过攻击者的主观选择消除冗余节点。但是未能分析攻击成本和节点概率的关联性,因而无法通过攻击成本对攻击路径进行预测。Li等人[16]通过生成攻击图前合并具有相同特征的主机来降低攻击图的规模,虽然这种方法可以有效地减少攻击图中节点和边的数量,但是它只适用于对一些特殊的网络进行脆弱性分析。文献[17]将攻击图转化成Petri网并进行扩展生成新的攻击模型,引入系统最大承受攻击能力概念,将攻击状态的二态性扩展到攻击成功、攻击失败、攻击被检测三个方面,具有很大的灵活性,但是没有考虑攻击之间的关联性对计算的影响。
针对上述不足,本文提出了一种旨在通过解决节点置信度的错误计算问题,提高预测准确性的方法。为此,本文引入了贝叶斯网络分隔定理,提出了节点置信度以及攻击行为发生的条件概率的计算方法,并给出了ConProb-Computing、InCon Prob-Computing、JoProb-Computing三个算法。通过量化攻击成本为攻击行为实施的可能性,提出了攻击行为发生的条件概率计算方法,解决了由攻击成本导致的条件概率错误计算问题;通过引入贝叶斯网络分隔定理及提出节点置信度计算方法,使具有关联性的节点在它们共有的d-分隔集合条件下相互独立,回避节点间相关性导致的节点置信度错误计算问题。相比前述文献,攻击行为发生的条件概率和节点置信度的计算方法以及计算算法的提出,不但提高了置信度计算的准确性和网络威胁传播路径预测的有效性;同时它们以贝叶斯网络为基础,能适用于更加复杂的网络,具有很好的扩展性。
2 贝叶斯攻击图和安全威胁节点概率计算
网络威胁的传播是一种复杂的多步骤过程,包含一系列基本资源状态的变化。基本资源状态的变化改变了网络的状态,使攻击者获得了一定级别的系统权限。同时,系统权限的获取将使攻击者进一步占有更多的资源。通常,网络管理人员可以依据基本资源状态的变化推断可能的网络威胁传播路径,并采取应对措施。
2.1 贝叶斯攻击图
贝叶斯网络本质上是一种因果关系图,描述了系统基本资源状态变化的因果关系。一方面,它包含了网络威胁所有可能的传播路径。此外,根据单调性假设,攻击者不会放弃已经占有的资源。因此,攻击者不会再为占有的资源实施攻击,即贝叶斯网络中不会出现循环攻击路径。根据以上分析,定义如下贝叶斯攻击图:
定义1贝叶斯攻击图G={V,E,W,P,Π}为具有一个或多个AND-OR节点的贝叶斯网络,其中:
(1) V(G)={V0∪VG}为资源状态节点集合。它是一个非空有限的AND-OR节点集合。节点表示攻击者攻击系统时需要占有的资源。成功改变资源状态时,对应节点的取值为True,否则为False。初始节点集合V0表示初始状态下攻击者以一定概率占有的资源。目标节点集合VG表示攻击者成功地改变一系列资源状态后,才能达到的最终目标节点集合。
(2) E(G)⊆V×V为关联各节点的有向边集合。如果e1,2=
(3) W为攻击权集合。∀w∈W均与每一节点关联,由二元组(h,m)表示。h表示攻击节点vi时,所选攻击路径上已花费的总攻击成本。m表示攻击节点vi时,所有经过节点vi的攻击路径需要花费的总攻击成本。
(4) P=(P1∪P2)。P1为攻击行为发生的条件概率。对于任意攻击行为,只有对应的前件节点满足条件时才能发生,所以P1=(攻击行为发生|Pre(vi)满足条件)={P2:(Pre(vi),vi)}→[0,1]。 P2为攻击步骤成功的概率。对于P2,只有攻击行为发生,攻击步骤才能成功,即vi=True。所以P2=(vi=True|攻击行为发生)={P2:(攻击行为发生,vi=True)}→[0,1]。
(5) Π(G)={π.V×V→[0,1]}为贝叶斯攻击图节点置信度分布。π(vi)表示攻击者当前已成功占有节点vi的概率。由于初始状态下起始节点v0已为攻击者成功占有,所以π(v0)=1.0。
定义2AND节点指的是节点vi的所有前件节点之间是AND操作,当且仅当所有前件结点均成功实施攻击行为时,才能将节点vi的值置为True。
定义3OR节点指的是节点vi的所有前件节点之间是OR操作,当且仅当任一前件结点成功实施攻击行为时,都能独立地将节点vi的值置为True。
根据以上定义,我们首先利用脆弱点扫描工具(例如X-Scan)对系统资源存在的安全漏洞进行扫描,得到资源状态节点;然后分析节点间的依赖关系,显示标出各个有向边;最后综合考虑节点间AND-OR节点的4种排列组合情况:AND-AND、AND-OR、OR-AND和OR-OR,生成目标系统的主干结构;并结合目标网络的安全状态,估计安全威胁的传播路径。依照上述方法,本文对小型局域网进行扫描,得到了图2所示的贝叶斯攻击图。

图2 贝叶斯攻击图
图2中,初始状态下,攻击者以概率π(v1)、π(v2)、分别占有资源状态节点v1、v2,其后,攻击行为遵循条件概率分布P1发生,相继占有对应的节点v3-v10,并最终占有目标节点v11。
2.2 安全威胁的传播路径
定义4给定贝叶斯攻击图,存在一个始于起始节点V0,终于目标节点VG的资源状态变迁序列Path,Path=V0→V1→…Vi→…Vn→VG,其中0≤i≤n,则称满足下述约束条件的变迁序列为安全威胁的传播路径:
(1) 变迁Vi的下一变迁Vi+1必为Vi的后件节点,反之,变迁Vi必为Vi+1的前件节点。
(2) 变迁序列Vi+1中的节点集合与初始节点和目标节点的交集必不为空。
(3) 变迁序列的长度是有限的。
(6)实行全天候通关制度。随着我国邮轮旅游业的日益发展壮大,我国邮轮旅客通关量增速明显,邮轮到达码头的时间有时候会是随机的,旅客通关时间也是随机的,现有的口岸通关还不能满足这种随时通关的需求,因此,邮轮口岸提供随机性的服务的也是必不可少的,邮轮口岸建立必要的小时通关制度,全天候为邮轮乘客提供通关服务,满足邮轮乘客便捷通关的需求。
对于图2,在所有符合定义4的变迁序列中,我们假设网络威胁会沿如下路径传播:
① V1→V3→V6→V9→V11
② V1→V4→V7→V9→V11
③ V8→V5→V8→V10→V13→V11
根据图2,攻击者相继占有路径①、②、③上的各个节点后,将会达到目标,此时:
(1) 若不考虑攻击成本和节点间的相关性,而只是简单地将各节点值置为True,则理论上,攻击者可以选择三条路径中的一条或者多条实施攻击,最终占有目标节点。
(2) 若考虑攻击成本,则容易发现,当攻击步骤花费成本Cost(e6,9)远大于Cost(e7,9)时,攻击者出于成本的考虑,会倾向于实施攻击步骤
(3) 若考虑节点间的相关性,节点V6和V7之间,V9和V7、V5之间均存在相关性。以节点V6和V7为例,根据条件独立假设,V7和V8独立地影响节点V9的置信度,即沿不同路径到达节点V9是互不影响的。考虑到成本因素,攻击者只会选取一条路径到达节点V9。这样,路径V7→V9可能性的增加必然会导致V6→V9可能性降低,反之亦然。因而,节点V6和V7之间存在相关性将会导致节点置信度的错误计算,影响对攻击路径的预测。
根据以上分析,网络威胁的传播路径问题可以描述为:
3 节点置信度的计算
贝叶斯网络本质上是因果攻击图,能够分析多步骤的网络攻击,展示网络安全威胁的传播路径。为了预测可能的传播路径,我们需要计算贝叶斯攻击图的节点置信度。
3.1 基础数据的获取
贝叶斯攻击图G={V,E,W,P,Π}能够展示网络安全威胁的传播路径,为了确定贝叶斯攻击图的节点置信度,必须首先获取攻击行为发生的条件概率,即p1和成功发生的条件概率p2,然后再计算节点置信度。
对于p2,其取值大小取决于资源状态的难易程度。根据CVSS标准,NVD数据库中的“AccessComplexity”属性值,它表征安全漏洞被利用的复杂程度,因而可以作为条件概率p2的概率值。根据CVSS标准,p2取值如表1所示。

表1 CVSS基本评价分值
对于p1,由于p1受到成本因素的影响,因此,我们将在下节对p1的概率值进行计算。
3.2 攻击成本Cost的计算
攻击过程中,资源状态的变迁通过一系列命令或操作实现。这其中,包括一些功能相似,实施成本不同的命令和操作。为了分析资源状态变迁的成本,我们可以依据功能的相似性,将这一过程中的命令和操作划分成不同的命令集合,称为元操作。
定义6元操作是具有相似功能的一类命令或操作的集合。
采用元操作的好处在于:
(1) 命令和操作成本易于统计,方便对攻击成本进行计算。
(2) 命令或操作的选取仅限于元操作,便于优化攻击成本。
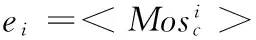
定义7从集合的角度定义了攻击步骤。贝叶斯攻击图中的∀e∈E(G),都是一个攻击步骤,用来完成一次资源状态变迁,是由若干命令或操作依照一定顺序组成的集合。图3显示了这种映射关系。

图3 攻击步骤和元操作映射关系
图3显示了元操作和攻击步骤的映射关系。Sub-Mos为元操作集合在攻击步骤上的映射,每个Sub-Mos子集与攻击步骤的一个功能相对应。因此,攻击步骤可以看成是由若干个元操作按照一定顺序组成的集合。由图3可知,同一元操作集合的操作序列不同,由它们所组成的攻击步骤不同。因此,一个攻击步骤的成本应包括元操作成本和操作序列成本,是二者的线性和。
定义8贝叶斯攻击图中,对于∀e∈E(G),每个攻击步骤需要花费的成本为:
Cost(e)=μ×Cost(Meta-operation)+η×Cost(Sequence)
(1)
定义8中,Cost(Meta-operation)为元操作执行成本,Cost(Sequence)为操作序列成本,μ、η为对应的参数。Cost(Meta-operation)的计算取决于元操作本身和资源的使用情况,因而,是元操作和资源数目的函数;Cost(Sequence)的计算取决于不同元操作的排列顺序,是操作序列和元操作的函数。目前,元操作执行成本和操作序列成本的计算还停留在理论阶段。因此,本文考虑将各攻击步骤的Cost值设为1。
定义9贝叶斯攻击图中,对于∀e∈E(G),攻击目标为节点d,d的攻击权为W(h,m),则攻击步骤e发生的条件概率P1(e)为:
(1) 如果d∈V0,P1(e)=1.0
(2) 如果d∈V且d∉V0,其有s个前件结点,用节点数组l[i]表示,对应的攻击步骤为e[i](0≤i≤s),则
1) 如果d既非AND节点,又非OR节点,那么:
2) 如果d为AND节点,那么:
P1(e[1])=P1(e[2])=…=P1(e[s])
3) 如果d为OR节点,且其s个前件结点对应的攻击步骤按照成本m由大到小的顺序依次排列为q[1],…,q[j],…,q[s]。那么:
同样的,我们可以计算出其他前件结点的条件概率P1[q[2]], P1[q[2]],…,P1[q[s]]。
定义9分析了攻击成本和攻击步骤发生概率之间的关系。
(1) 初始节点。初始状态下,引发初始节点状态改变的攻击步骤已经发生。因此,P1(e)=1.0。
(2) 非初始节点。① d为非AND节点和非OR节点,即d的前件结点只有一个。这种情况下,条件概率P1是已消耗的攻击成本h(e[i])与沿此路径占有i结点需要消耗的总成本m(e[i])的比。它表示攻击者实施此攻击步骤的可能性。攻击步骤成本Cost占有m(e[i])的比例越小,攻击者实施此次攻击的可能性越小。② AND节点。对于AND节点,攻击者只有同时实施攻击步骤,才能到达节点d。因此,攻击者实施各攻击步骤的可能性是相同的,故有P1[e[1]]=P1[e[2]]=…=P1[e[s]]。③ OR节点。对于OR节点,我们知道,攻击者只要沿一个攻击步骤实施攻击,即可到达节点d。由于攻击成本的增加会降低攻击者实施攻击行为的可能性,因此,对于攻击成本最高的攻击步骤,其发生的条件概率越小。P1[q[1]就是赋予攻击成本最高的攻击步骤最小的实施可能性,赋予攻击成本最低的攻击步骤最大的实施可能性。
3.3 节点置信度的计算
贝叶斯网络中,之所以存在着节点置信度的错误计算问题, 根本原因是节点间存在着相关性。为了解决这一问题,我们给出如下定理。
定理1贝叶斯攻击图中,假设存在任意节点集合D={d1,d2,…,dk}和N={n1,n2,…,nk},其中D,N⊆V,那么:

(2)
证明:对于任意的D,N⊆V,由贝叶斯定理:
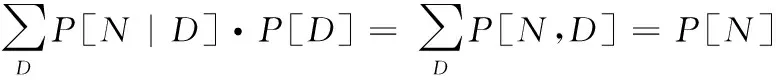
定理2贝叶斯攻击图中,假设存在任意节点集合D={d1,d2,…,dk}和N={n1,n2,…,nk},其中D,N⊆V,且集合D中所有节点取值已知情况下,集合V中的节点相互独立,那么:
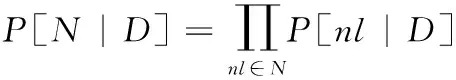
(3)
对于集合N,组成它的节点之间总是存在关联性。为了准确地计算各节点的联合概率P{n1,n2,…,nk},我们可以首先寻找到集合D,使集合N中各节点相互独立,然后依据式(2)和式(3),在条件独立的情况下计算其联合概率。
d-分隔是贝叶斯网络中,对于3个两两交空的集合X、Y和Z,判断X和Y在给定Z时的条件独立性。为了找到使集合N中各节点相互独立的节点集合D,本文引入了d-分隔。
定义10贝叶斯攻击图中,对于两两交空的节点集合X和Y,如果存在一些节点v∈V,使得v是节点x∈X和节点y∈Y的分连节点,那么由v、d-分隔v的祖先节点和d-分隔v的祖先节点的节点所组成的集合D(D⊆V)d-分隔X和Y。
根据定义10,如果D中所有节点的值已知,那么X和Y中所有元素相互独立,记为X⊥Y|D。条件概率记为φ({X,Y},D)。为方便叙述,令N=X∪Y,则φ({X,Y},D)=φ(N,D)。
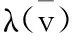

(4)

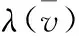
(1) 当W=AND时:
(5)
(2) 当W=OR时:
(6)
考虑到节点之间的关系为AND或OR,会对置信度的计算结果产生影响,因此,定义12在定义11的基础上进行了推广,使之能用于计算节点之间的关系为AND或OR等情况下的节点置信度。
3.4 节点置信度的计算举例
考虑到节点置信度的计算需要计算攻击步骤发生的条件概率P1,我们给出图4所示的贝叶斯攻击图。图4中,我们假设各攻击步骤的取值为True,对应的攻击成本为1。

图4 贝叶斯攻击图-攻击成本
在计算P1时,我们将从初始节点开始,采用递归的方法,逐层推进。具体的计算方法见定义9,计算步骤如下(计算时我们假设初始节点的攻击权为W(1,1)):
(1) 依据定义9,占有初始节点v1、v2的攻击步骤发生的条件概率均为1.0。
(2) 结合攻击权定义,我们得到节点v3、v4、v5攻击权为W(v3)=(1,2),W(v4)=(1,2),W(v5)=(1,2),依据定义9对非初始节点条件概率的定义,P1(e1,3)=P1(e1,4)=P1(e2,5)=1/2。
(3) 分别计算节点v6、v7、v8攻击权为W(v6)=(4,6),W(v7)=(4,6),W(v8)=(2,3),依据定义9对AND和OR节点的条件概率定义,P1(e3,6)=1/2,P1(e4,6)=1/2,P1(e4,7)=P1(e5,7)=2/3,P1(e5,8)=2/3。
(4) 计算节点v9、v10攻击权为W(v9)=(10,12),W(v10)=(3,4),P1(e6,9)=1/2,P1(e7,9)=1/2,P1(e8,10)=3/4。
(5) 计算节点v11攻击权为W(v11)=(13,16), P1(e9,11)=11/16,P1(e10,11)=4/16。
获得攻击步骤的条件概率后,我们可以依据定理1和定理2,以及定义10和定义11计算各节点的概率。下面以λ(v6)为例来说明节点置信度的具体计算方法。
图4中,Z(v6)={v3,v4},Z(v7)={v4,v5},D(v6)={v1∪D(v4)}∩{v1∪D(v3)}={v1},D(v7)={v1∪D(v4)}∩{v2∪D(v5)}=∅。因此:
(定义12)
(定理2)
(定理2)
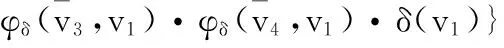
(1-P1(e4,6)·P2(e4,6)·P1(e1,4)·P2(e1,4))·(P1(e1,3)·
P2(e1,3)·P1(e1,4)·P2(e1,4)}
(定义10-12)
按照上述计算方法,我们最终得到的各节点置信度如表2所示。

表2 贝叶斯攻击图节点置信度
3.5 节点置信度的计算算法
为了计算贝叶斯攻击图的节点置信度,本文设计了如下的3个算法。
算法1是一个条件概率计算算法,用来计算攻击步骤发生的条件概率。对于贝叶斯攻击图中的任一节点,该算法都能计算出欲到达该节点,所选攻击路径上已消耗的总攻击成本h和需要消耗的总攻击成本m,并根据节点类型,返回对应的比值。这个比值就是攻击步骤发生的条件概率。具体的计算方法见定义9。
算法1条件概率计算算法 ConProb-Computing (G,Cost)
描述:本算法将依据贝叶斯攻击图G和攻击步骤实施成本Cost,计算攻击步骤发生的条件概率P1。
输入:贝叶斯攻击图G,攻击步骤成本Cost,攻击权W(h,m)。
输出:攻击步骤发生的条件概率P1。
1. IF节点v是初始节点 THEN{W(h,m)=W(1,1)}
2. RETURN P1(v)=1.0
//初始节点攻击步骤条件概率
3. END IF
4. IF节点v是非初始节点 THEN
5. h←SUM(节点v的所有前件结点对应的h值)
6. m←h+SUM(节点v的所有前件结点对应的Cost值)
7. END IF
8. IF节点v是AND节点 THEN
9. A对于∀d∈ Pre(v),P1(ed,v) = h/m
//引发AND节点的攻击步骤具有相同的发生概率
10. END IF
11. IF节点v是OR节点 THEN
12. 将所有前件结点d依据各节点h(q(i))+Cost(q(i))值由大到小编入队列QUENE(r)
13. QUENE(r)={r1,r2,…,rn}
14. 将所有前件结点d依据各节点

16. 值由到大编入队列QUENE(q)
17. QUENE(q)={q1,q2,…,qn}
18. IF r1是QUENE(r)中最小值,q1是QUENE(q)中最大值,THEN
19. QUENE(r)←{r1,r2,…,rn}
20. QUENE(q)←{q1,q2,…,qn}
21. RETURN P1= q1
22. 对于∀d∈ Pre (v),调用步骤18,
23. RETURN P1= qi
24. END IF
25. ELSE IF节点v既非OR节点又非AND节点 THEN
26. P1=h/m
27. RETURN P1=h/m
算法2也是一个条件概率计算算法,用来计算节点集合D发生情况下,节点集合N被成功占有的条件独立概率φδ(v,D)。由于φδ(v,D)=P1[e[z]]×P2[e[z]]×φ(z,D)(定义11),因此,本算法在φδ(v,D)时,主要步骤包括:1)单个节点n在集合D不同取值情况下的条件概率φ({n},D); 2)依据集合N中不同节点的类型,将φδ(v,D)转化为φ(z,D)形式进行计算。(定理2、定义11和定义12); 3)依据上述步骤,最终返回条件独立概率φδ(v,D)。具体的计算方法见定理2、定义11和定义12。
算法2条件独立概率算法 InConProb-Computing φδ(v,D)
描述:本算法将依据贝叶斯攻击图G和攻击步骤发生的条件概率P1和成功实施的条件概率P2,计算节点集合D发生情况下,节点集合N被成功占有的条件独立概率φδ(v,D)。
输入:贝叶斯攻击图G,节点集合N,d-分隔节点集合N中所有节点的集合D,P1,P2。
输出:φδ(v,D)。
1. N←{n0,n1,…,nq}
2. D←{d0,d1,…,dk}
3. IF 集合N中元素个数大于1 THEN
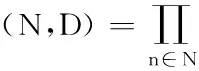


7. IF N和D中元素相同THEN
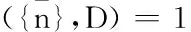
9. IF D中有元素取值为False THEN
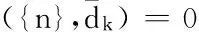
11. IF集合N中节点为初始节点 THEN
12. RETURN φδ(N,D)=1
13. IF集合N中节点不全为初始节点 THEN
14. 遍历搜索N中各节点的前件结点集合Z
15. IF n为AND节点 THEN

17. RETURN φδ(v,D)
18. IF n为OR节点 THEN
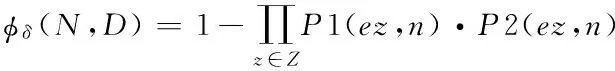
20. RETURN φδ(v,D)
21. IF 集合Z中只有一个节点 THEN
22. φδ(N,D)=P1(ez,n)·P2(ez,n)
23. RETURN φδ(v,D)
算法3为节点联合概率计算算法,用来计算节点置信度λ(v)。对于任意节点,如果为初始节点,那么λ(v)为1.0;如果为非初始节点,那么首先依据其前件节点的个数分为两种情况:前件结点个数大于1或者等于1。对于前件结点个数大于1的节点,再依据其d-分隔节点集合是否为空集,分为空集和非空集两种情况来计算得到。依据上述算法最终返回结果即为各节点置信度。具体的计算方法见定义11、定义12和定理1以及定理2。
算法3节点联合概率计算算法JoProb-Computingλ(n)
描述:本算法将依据贝叶斯攻击图G和算法2得到的φδ(v,D)贝叶斯攻击图G的节点置信度λ(n)。
输入:贝叶斯攻击图G,节点集合N,d-分隔节点集合N中所有节点的集合D,P1,P2,φδ(v,D)。
输出:λ(n)。
1. N←{n0,n1…,nq}
2. D←{d0,d1…,dk}
3. IF节点n为初始节点 THEN
4. RETURN λ(n)
5. IF节点n为非初始节点 THEN
6. 遍历搜索N中各节点的前件结点集合Z
7. IF 集合Z中只有一个节点 THEN
8. λ(n)=P1(ez,n)·P2(ez,n)·λ(z)
9. RETURN λ(n)
10. IF 集合Z中有多个节点 THEN
11. 查找d-分隔n的集合D
12. IF D(Z)=∅ THEN
13. IF n为AND节点 THEN
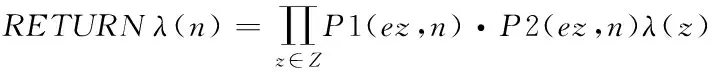
15. IF n为OR节点 THEN

17. IF D(Z)不为空集 THEN
18. IF n为AND节点 THEN
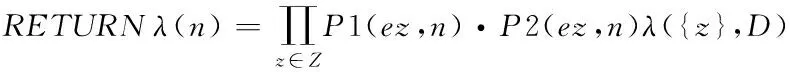
20. IF n为OR节点 THEN

4 实验设计与分析
为了验证节点置信度计算方法的有效性,本文设计了基于Windows系统的小型局域网,并用Java语言实现了算法1、算法2和算法3。
4.1 实验网络配置
图5为试验用局域网拓扑图。实验网络以防火墙为界,将互联网与局域网内的M1、M2、M3 3个安全区域分别隔开。攻击主机Attack通过Internet访问局域网。
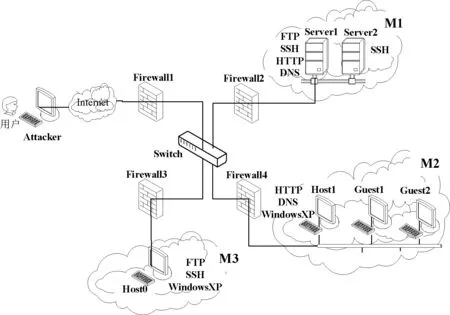
图5 局域网拓扑图
局域网中,M1区域设置有SQL服务器(Server1)和历史数据服务器(Server2),并通过Firewall2与其他网络相隔离。Server1负责对Server2进行数据备份,并为M1和M2区域的各主机提供FTP、SSH、HTTP、DNS等服务,为Server2提高SSH服务;M2区域中,Host1开放HTTP和DNS服务;M3区域中,Host0为存储有重要数据的目标主机,开放FTP和SSH服务。
4.2 实验数据及分析
利用Scanner对实验网络进行扫描,得到的各主机漏洞及漏洞信息如表3所示。各漏洞被利用的难易程度量化值可以通过查询NVD数据库中的“AccessComplexity”属性值获得,查询结果见表4所示。

表3 各主机漏洞信息
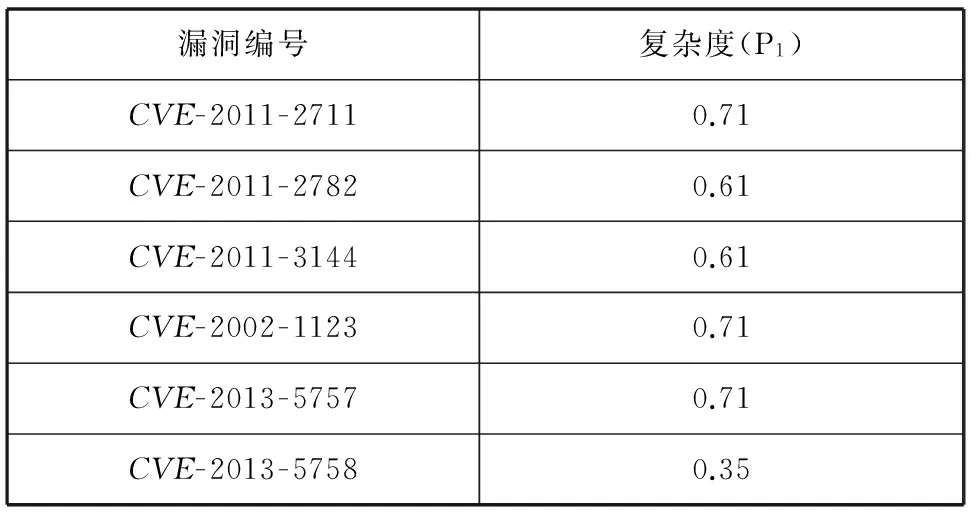
表4 各主机漏洞信息量化
应用前文提出的3个算法,我们对图4所示的贝叶斯攻击图节点置信度进行了计算。首先,我们利用传统节点置信度计算方法(不考虑攻击成本和节点间相关性),对图4的节点置信度进行计算,计算结果见表5所示。
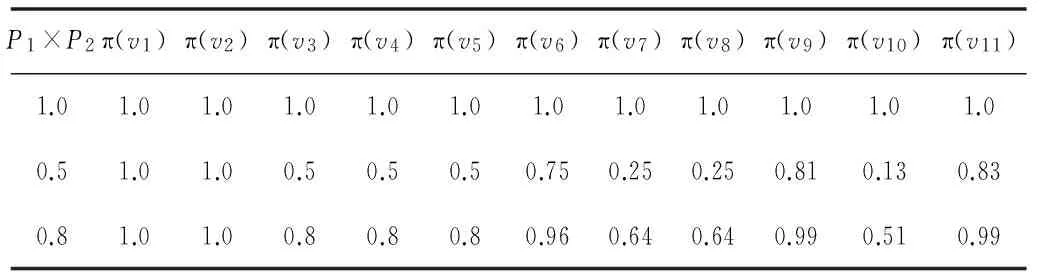
表5 传统节点置信度计算方法计算结果
图4中,需要明确攻击路径的节点是v3和v4、v6和v7、v9和v10。由于传统的计算方法不考虑攻击成本和节点间相关性的影响,因此,我们假设攻击者占有资源节点的条件概率是固定值(固定值分别设置为1.0、0.5、0.8)。
对于v3和v4、v6和v7、v9和v10三对节点中,v6和v7、v9和v10两对节点的置信度在条件概率为1.0时,均相等,而在条件概率为0.5和0.8时则不相等。之所以出现这种结果,从图4中我们可以看到,节点v6和v7除了同时受到节点v4的影响,v6还受到了v3的影响,而v7则同时受到了v5的影响,这在一定程度上相当于改变了攻击者占有资源节点v6和v7的条件概率。对于v9和v10,也是如此。因此,符合传统计算方法条件的只有v3和v4。
从表3中可以看出,在不考虑攻击成本和节点间相关性的影响下,v3和v4的节点置信度总是对称相等的。这意味着,我们无法通过节点置信度来判断攻击者选择了哪条攻击路径。
而后,我们考虑考虑攻击成本和节点间相关性对节点置信度计算结果的影响,并利用本文方法做了实验,得到的节点置信度计算结果见表6所示(i表示试验编号,i不同,计算节点置信度的攻击成本或者条件概率也不同)。

表6 本文节点置信度计算方法计算结果
i=1时,我们假设各攻击步骤消耗的攻击成本均为1且P2(e1,3)> P2(e1,4),因而π(ν3)>π(ν4),明确了攻击路径。
i=2时,保持其他节点条件不变,只改变攻击步骤e6,9、e7,9成功的条件概率。由于节点v9和v11与v6和v7相关,因而,表中的节点v9和v11的置信度亦随之发生了变化。与i=1时相比,解决了节点相关性对节点置信度计算结果的影响。
i=3时,我们假设与节点v4相关的条件不变,增大Cost(e13)和Cost(e25)。基于这种假设得到的π(ν6)小于前两种假设。这归因于节点v4和v3对v6的共同影响。在v4和v3间为OR节点,且v4相关条件不变的情况下,随着Cost(e13)的增加,v3对v6的影响必然降低,因而,与i=1和i=2相比,π(ν6)减小。另一方面,基于这种假设得到的π(ν7)大于前两种假设。这是因为影响v7的节点v4和v5间为AND关系,其中一方对v7影响的增大,必然导致π(ν7)的增大。因而,与i=1和i=2相比,π(ν7)增大。
所以,本文提出的计算方法有效地解决了节点置信度错误计算问题,明确了攻击路径。
4.3 攻击路径的预测
为了预测攻击路径,我们引入成本比率参数C(X),用来分析攻击成本对攻击者所选攻击路径的影响。我们以图2中的v3和v4为例,分析Cost(e13)和Cost(e14)对e13和e14的影响。这其中,我们设定参数C(X)=Cost(e13)/Cost(e14),它表示攻击者实施攻击步骤e13和e14需要花费的成本比值。
依据参数C(X)的设定,我们对攻击者实施攻击步骤e13或e14的可能性进行预测,动态生成节点v6的置信度走势图。图6显示了节点v6随C(X)变化的置信度走势图。X轴表示成本比率C(X),Y轴表示置信度,红线表示节点v6的置信度π(ν6),平行于X轴的黑线为阈值,表示攻击者想通过实施攻击步骤e13成功占有节点v6,节点v6的置信度必须达到的最小值。

图6 攻击路径预测
图6中,随着参数C(X)的增大,π(ν6)呈现出逐渐减小的趋势。其阈值为0.23,表明攻击者想通过实施攻击步骤e13成功占有节点v6,π(ν6)的最小值必须达到0.23。此时,对应的C(X)值为0.33。由此我们得出结论,当C(X)值不大于0.33时,攻击者会选择通过路径e13到达节点v6。因此,结合管理人员设定的阈值,如本文的0.23,和成本比率预警值,当攻击者选择某一路径的成本比率达到预警值时,就能做出预警,并采取相应措施。
目前,有关攻击路径的预测算法大致分为以下两类:1) 包含攻击图模型以及模型内部系统风险因素的概率分布的二元组模型;2) 利用系统风险因素之间的关系,对系统的可靠性进行分析评估。其中,第一类算法能够快速地对模型进行构建,能准确地找出系统风险的关键点,但在实际的攻击路径传播中,风险因素间的相关性,以及目标节点的复杂性及重要性的不同,都可能导致节点概率的错误计算,影响预测的准确性。第二种算法考虑到以上的问题,并针对这些问题做出了相应地解决办法,在一定程度上提高了预测的准确性,但是模型的复杂程度也随之加大,并不具备良好的扩展性。
本文中基于d-分隔定理的节点置信度计算方法通过对攻击成本的量化,使其成为攻击行为实施的可能性,能更为准确地计算出节点发生的概率。提出利用贝叶斯网络分隔定理的节点置信度计算方法,能使节点间的相关性对节点置信度计算的影响达到最小。相比以上的两类攻击路径预测算法,本文的算法有以下三个优势:1)通过对攻击行为发生的条件概率,提高了置信度计算的准确性;2)节点置信度的准确性的提高,使网络威胁传播路径预测更为有效;3)该算法以贝叶斯网络为基础,能适用于更加复杂的网络,具有很好的扩展性。
5 结 语
为了解决节点相关性和条件概率导致的节点置信度错误计算问题,提高网络安全威胁传播路径预测的有效性,本文提出了一种节点置信度计算方法。围绕这一方法,定义了贝叶斯攻击图G,引入了d-分隔定理,提出了攻击行为发生的条件概率和节点置信度的计算公式,并给出了节点置信度的计算算法。上述内容的提出,不但弥补了Homer[6]文中的不足,考虑了条件概率对节点置信度的影响,而且提出了条件概率的计算公式,这在文献[12,13]中并未被提出。针对文献[14,15]的不足,本文还分析了攻击成本对攻击者选择策略和节点概率的影响。最后,通过对实验结果进行分析,本文提出的方法能够很好地提高节点置信度的计算准确性,提升网络威胁传播路径预测的有效性。
进一步研究工作包括深入研究网络安全威胁传播路径存在的问题以及在更为复杂的网络中验证本文所提方法的有效性。
[1] 黄家林, 张征帆. 主动防御系统及应用研究[J].网络安全技术与应用, 2007(3):48-51.
[2] 陈锋, 张怡, 苏金树,等.攻击图的两种形式化分析[J].软件学报,2010,21(4):838-848.
[3] 吴迪, 连一峰, 陈恺,等. 一种基于攻击图的安全分析与识别方法[J].计算机学报,2012,35(9):1938-1950.
[4] Changhe Yuan,Brandon Malone. Learning optimal bayesian networks: a shortest path perspective[J]. Journal of Artificial Intelligence Research, 2013,48(1):23-65.
[5] 陈锋, 毛捍东, 张维明, 等. 攻击图技术研究进展[J]. 计算机科学,2011,38(11):12-18.
[6] Homer J, Ou X M, Schmidt D. A sound and practical approach to quantifying security risk in enterprise networks[R]. Technical report, Kansas State University, 2009.
[7] Mell P, Scarfone K. A Complete Guide to the Common Vulnerability Scoring System Version 2.0[EB/OL].2007. http://www.first.org/cvss.
[8] Common Vulnerability Scoring System version2[EB/OL]. 2011. http://www.cvss.org.
[9] Yu D, Frincke D. Improving The Quality Of Alerts And Predicting Intruder’s Next Goal With Hidden Colored Petri-Net[J]. Computer Networks, 2007,51(3):632-654.
[10] 石进, 郭山清. 一种基于攻击图的入侵响应方法[J]. 软件学报,2008,19(10):2746-2753.
[11] Mehta V, Bartzis C, Zhu H, et al. Ranking Attack Graphs.[J]. Proceedings of Recent Advances in Intrusion Detection, 2006,4219:127-144.
[12] 张少俊, 李建华, 宋珊珊,等. 贝叶斯推理在攻击图节点置信度计算中的应用[J]. 软件学报, 2010,21(9):2376-2386.
[13] Publishing S. A Novel Attack Graph Posterior Inference Model Based on Bayesian Network[J].Journal of Information Security,2011,2(1):8-27.
[14] Wang S, Zhang Z, Kadobayashi Y. Exploring attack graph for cost-benefit security hardening: A probabilistic approach[J]. Computers & Security, 2013, 32(1):158-169.
[15] 吴泓润, 覃俊, 郑波尽. 基于代价的复杂网络抗攻击性研究[J]. 计算机科学, 2012,39(8):224-227.
[16] Li W, Vaughn R B. Cluster Security Research Involving the Modeling of Network Exploitations Using Exploitation Graphs[C]//Proc of the 6th IEEE International Symposium on Cluster Computing and the Grid Workship, 2006:26-37.
[17] 黄光球,程凯歌. 基于攻击图的扩充Petri网攻击模型[J].计算机工程,2011,37(10):131-133,136.
NODE CONFIDENCE CALCULATION METHOD BASED ON D-SEPARATION THEOREM OF BAYESIAN NETWORK
Wang Hui Kang Kaihang Wang Yunfeng
(School of Computer Science and Technology, Henan Polytechnic University, Jiaozuo 454000,Henan,China)
Current node confidence calculation method for Bayesian network has the problem of node confidence miscalculation caused by the miscalculation of conditional probability and the correlation of nodes. This problem reduces the accuracy of node confidence and impacts the effectiveness of prediction on propagation paths of network threats. Therefore, we present a node confidence calculation method which is based on d-separation theorem of Bayesian network. First, by analysing the correlation between attack cost and the occurrence likelihood of attack activity, we propose an approach for calculating the conditional probability of attack activity occurrence so as to solve the problem of miscalculation in conditional probability. Secondly, by introducing separation theorem of Bayesian network, we make the nodes with correlation be independent to each other under the condition of their common d-separation set, and propose the node confidence calculation method so as to effectively avoid the miscalculation of node confidence caused by the correlation. Finally, experimental results show that our method effectively solves the miscalculation problem of node confidence and improves the accuracy of node confidence, consequently it achieves the effective prediction on propagation paths of network threats.
Node confidence Conditional probability Correlation d-Separation Attack cost
2015-07-16。国家自然科学基金项目(51174263,6130 0216);教育部博士点基金项目(20124116120004);河南省教育厅科学技术研究重点项目(13A510325)。王辉,副教授,主研领域:计算机网络及网络安全,无线传感器网络。亢凯航,硕士生。王云峰,硕士生。
TP393.08
A
10.3969/j.issn.1000-386x.2016.11.066
