基于群体划分优化的GAP-RBF神经网络学习算法

包沁昕 宋 威

(江南大学物联网工程学院 江苏 无锡 214122)



基于群体划分优化的GAP-RBF神经网络学习算法

包沁昕 宋 威

(江南大学物联网工程学院 江苏 无锡 214122)

针对传统GAP-RBF算法学习精度不够高的问题，提出一种基于群体划分优化的GAP-RBF网络学习方法。首先，为了克服传统GAP-RBF中存在的大型矩阵的计算问题，用DEKF(Decoupled EKF)方法调整网络参数；其次，为了获得学习精度更高的网络模型，算法利用基于PSO和GA的群体划分优化方法来训练隐含层和输出层的连接权值以及偏移项。实验结果表明，与RAN、RANEKF、MRAN和GAP-RBF算法相比，提出的算法可获得更精简的网络结构，同时提高了学习精度。

径向基函数神经网络 增长剪枝径向基函数算法 粒子群优化算法 遗传算法

0 引 言

近年来，随着人工智能、机器学习、数据挖掘等方面的发展，神经网络的研究受到了学者们的广泛关注。在众多的神经网络模型中，径向基函数RBF神经网络能够解决复杂非线性问题，在模式识别、回归分析和动态建模等领域得到了广泛的应用[1-4]，并且具有推广能力好，学习方法速度快，精度高，网络拓扑结构简单等特点。

针对RBF网络结构设计的问题，近年来相继提出了一些动态的构造方法。1991年，Platt提出了一个动态的资源分配网络RAN[5]，它可以根据输入数据的新颖性动态地增加隐层神经元，在没有新的神经元增加时，使用LMS(Least Mean Squares)方法调整网络参数，但是网络存在收敛速度过慢的问题。文献[6]中给出的RANEKF算法利用扩展卡尔曼滤波器EKF(Extended Kalman Filter)代替原LMS方法更新网络参数，算法的收敛速度和训练精度得到了提高，但也加大了网络结构的复杂度和计算负担，并且不能够删除冗余的神经元。针对这一问题，Lu等人提出了一种最小资源分配网络MRAN(Minimal RAN)算法[7]，它引入输出误差的RMS值和滑动窗口作为判断增长和删除隐层神经元的条件。虽然MRAN算法得到了精简的网络，但需要太多的调整参数，参数值的选择是非常困难的。文献[8]提出的GAP-RBF(Growing and Pruning RBF networks)算法采用隐层神经元重要性的概念作为增长和删除神经元的判断准则，减少了可调参数的个数，并且仅调整距离当前输入样本最近的隐层神经元的相关参数，大大降低了网络计算的复杂性。但是对于一些实际问题，相比MRAN算法，GAP-RBF的学习精度不是很高。

本文在GAP-RBF网络的基础上，提出了基于PSO[9]和GA[10]的群体划分优化的GAP-RBF算法(OGAP-RBF)。通过优化网络隐含层和输出层之间的连接权值以及偏移项来提高网络的学习精度。不同于原始EKF算法，本文采用DEKF(Decoupled EKF)[11]方法调整网络参数以降低网络计算复杂度和训练时间。通过3个Benchmark问题，对本文提出的算法进行计算机仿真并与其他算法做比较，结果表明此算法是一种稳定并且有效的学习方法。

1 PSO算法和GA算法

1.1 PSO算法

PSO粒子群优化算法是由Kennedy 博士于1995 年提出的一种新的基于群体智能的优化算法[9]。它源于对鸟类捕食行为的模仿，在基本PSO算法中，搜索空间中的每一个粒子都是优化问题的可选解[12]。

假设在一个n维的搜索空间，种群包括m个粒子P=(p1,p2,…,pm)，其中第i个粒子的位置为pi=(pi1,pi2,…,pin)，它的速度为vi=(vi1,vi2,…,vin)。粒子i目前最好的位置称为个体最优解Bi=(bi1,bi2,…,bin)，整个群体中最好个体的位置称为全局最优解Bg=(bg1,bg2,…,bgn)。在每次迭代中，每一个粒子搜索合适的解，以获得更好的适应值，根据以下公式来调整自己的速度和位置：

vid(t + 1)= ωvid(t)+ c1r1(bid(t)-pid(t)) + c2r2(bgd(t)-pid(t))

(1)

pid(t + 1)= pid(t)+ vid(t + 1)

(2)

其中，d=1,2,…,n,i=1,2,…，m，m为群体大小，pid(t)和vid(t)分别是时刻t时粒子i的位置和速度，pid(t + 1)和vid(t + 1)是下一时刻的更新。c1和c2称为学习因子，通常取常数。r1和r2是取自(0,1)之间的相互独立的随机数，ω称为惯性因子，可以随着迭代次数线性地减小。

由于对一些具有潜在最优解的问题PSO算法表现不佳，所以它的全局搜索能力可以进一步提高[13]。由于遗传算法获得局部极小值的概率很小，因此，PSO算法可以与GA算法相结合，得到全局最优解[14]。

1.2 GA算法

遗传算法是一类基于自然选择和遗传理论的有效优化方法，由美国Holland教授提出的[10]，它应用在RBF网络中具有全局的搜索和优化能力[15]。它可以解决非线性问题，通过对全局空间的搜索，根据遗传算法的选择，交叉和变异操作，以获得所需的解。

GA算法基于一个有染色体组成的群体，每个染色体都对应于问题空间的一个解，问题的求解表示为染色体优胜劣汰的过程。群体中的染色体并行的进行进化，在每一阶段，随机的选择染色体来产生下一代的个体。GA算法是一种有效的方法，因为它的理论是计算编码，而不是参数，每个染色体的适应度直接关系到目标函数。正是由于它相对的简单性和鲁棒性而变得越来越流行[16]。

算法开始时随机地生成初始群体，每个染色体由适应度函数来评价，之后每代群体根据适应值来复制或者淘汰。GA算法每次迭代主要包括以下步骤：

第一步选择操作 选择操作也被称为复制操作，是以一定的概率从父群体中选取下代个体，根据个体的适应度函数值决定他的优劣性。在本文中，使用最流行的转轮法进行选择操作，个体的适应度值越大，它被选取的概率越高。为了提高选择的质量和效率，最好的个体可以直接复制到下一代群体中。

第二步交叉操作 从群体中随机选择2条染色体，并在这2个父代染色体中随机选择一个位置，采用两点交叉的方法对两个染色体进行交叉，产生两个新的染色体。

第三步变异操作 每个染色体按照变异概率随机选择几个点，取随机值替换原有值，产生新的染色体，因此变异操作是一个随机搜索的过程。

由于GA算法收敛速度相对较慢，与PSO算法结合可以提高其搜索效率[17]。

2 群体划分优化GAP-RBF算法

本文提出的群体划分优化GAP-RBF算法(OGAP-RBF)主要过程包括：先用基于DEKF的GAP-RBF方法构建网络结构，获得网络的初始权值。在此基础上，利用基于PSO和GA的群体划分方法进一步优化GAP-RBF网络的权值和偏移项，最终得到最优的网络结构。

2.1 基于DEKF的GAP-RBF算法

对于一个GAP-RBF网络，具有K个隐层神经元，给定输入向量x∈Rl，则网络输出为：

(3)

其中φk(x)是第k个隐层神经元的响应：

(4)

其中，αk是连接隐含层与输出层的权值，μk是第k个隐层神经元的中心，σk为对应高斯函数的宽度。GAP-RBF的学习过程包括对隐层神经元的增加和删除以及参数的调整。在开始学习之前，网络没有隐层神经元，当输入样本(xn,yn)到达网络时，判断是否满足增加隐层神经元的条件，增加准则如下：

(5)

其中，en=yn-f(xn)为期望输出和网络输出之间的误差，μnr是距离输入样本xn最近的隐层神经元的中心，emin为网络输出的期望误差。εn为输入空间的分辨率，开始时εn=εmax， εn随着样本的输入按指数衰减：εn={εmaxγn,εmin}，εmax和 εmax分别为输入数据之间的最大和最小距离，γ为衰减常数：0<γ<1。Esig(k)是第k个隐层神经元的重要性，神经元重要性的定义为在目前到达网络的所有样本中对网络输出的平均贡献度，根据文献[8]的推导，它可以近似地表示为如下公式：

(6)

其中S(X)是整个输入空间的大小，l是输入空间的维度。当一个输入样本满足式(5)的条件时，增加一个新的隐层神经元，其相关参数为：

(7)

其中κ为重叠因子，用来确定隐层神经元的相应宽度。

当输入样本不满足增加准则时，本文使用DEKF方法调整距离当前样本最近的神经元的相关参数，相比原算法中的EKF方法，大大地降低了计算时间和计算复杂度[18]。在t时刻参数的调整过程如下：

K(t)=P(t)B(t)[R(t)+BT(t)P(t)B(t)]-1

(8)

w(t+1)=w(t)+K(t)e(t)

(9)

P(t+1)=[I-K(t)BT(t)]P(t)+Q(t)I

(10)

式中，R(t)为测量噪声方差，B(t)是与输出有关的参数的偏导数，P(t)是误差协方差矩阵，K(t)是卡尔曼增益向量，w(t)是参数矩阵，e(t)是输出误差，Q(t)是为了避免局部最小值收敛的人造过程噪声。

DEKF方法的关键在于它忽略互相排斥的神经元组的相关性，即忽略误差协方差矩阵P中的交互相关的元素。当DEKF方法中一个神经元的参数调整时，P中这个神经元与其他神经元交互相关的元素假设为0。此外，对于一个单独的神经元，其中心、宽度和权值也假定不相关的。

在参数调整之后，为了保证网络的精简需要删除重要性较低的隐层神经元。检查距离当前输入样本最近的神经元，如果满足删除准则：

(11)

即第nr个神经元对网络的输出贡献小于期望的精度，则删除这个神经元。

2.2 群体划分优化方法

群体划分优化方法是本文提出的一种融合了PSO算法和GA算法的新的优化方法。为了使PSO的局部搜索和GA的全局搜索同时进行，将群体进行划分。根据群体的适应度值将群体进行排序，划分为相等的两部分，PSO算法作用于适应度值较好的一部分，GA算法作用于适应度值较差的一部分，实现两种算法的并行搜索。

在RBF网络中，连接隐含层和输出层的权值和偏移项对网络至关重要，不合适的值直接影响网络的有效性和精确度。原始GAP-RBF算法中网络没有设置偏移项，本文在群体划分优化时加入对偏移项的优化以获得更合适的网络。由于GAP-RBF网络对样本只学习一次，之后用群体划分方法进行优化可以使样本得到充分地训练，提高网络的学习精度。改进的优化GAP-RBF算法(OGAP-RBF)包括两个学习阶段：在顺序学习阶段当所有新样本输入网络后，网络获得一个初始的结构；然后在优化阶段基于学习过的历史样本使用群体划分方法对网络的权值和偏移项进行优化以获得最优的网络模型。

本文提出的群体划分优化方法结合了PSO算法和GA算法，群体由PSO中的粒子和GA中的染色体组成。群体中的每个个体表示一组权值和偏移项的可选值。经过原始GAP-RBF网络的学习，获得权值的初始值，再通过群体划分优化的迭代计算逐步获得最优解。

在群体划分优化初始化群体时，其中一个个体由顺序学习阶段GAP-RBF获得的权值和随机偏移项构成，其他个体在一定的范围内随机产生。本文定义网络实际输出和期望输出之间的均方误差函数作为适应度函数，搜索最合适的权值和偏移项以获得最小的均方误差。适应度函数定义如下：

(12)

其中，ei是第i个样本实际输出与预期输出之间的误差。

群体包含m个个体，将群体划分为大小相等的两部分, 如图1所示。pm代表第m个个体，所有个体按照适应度排序如下：

fit(p1)≤fit(p2)≤…≤fit(pm/2)≤fit(pm/2+1)≤…≤fit(pm)

(13)

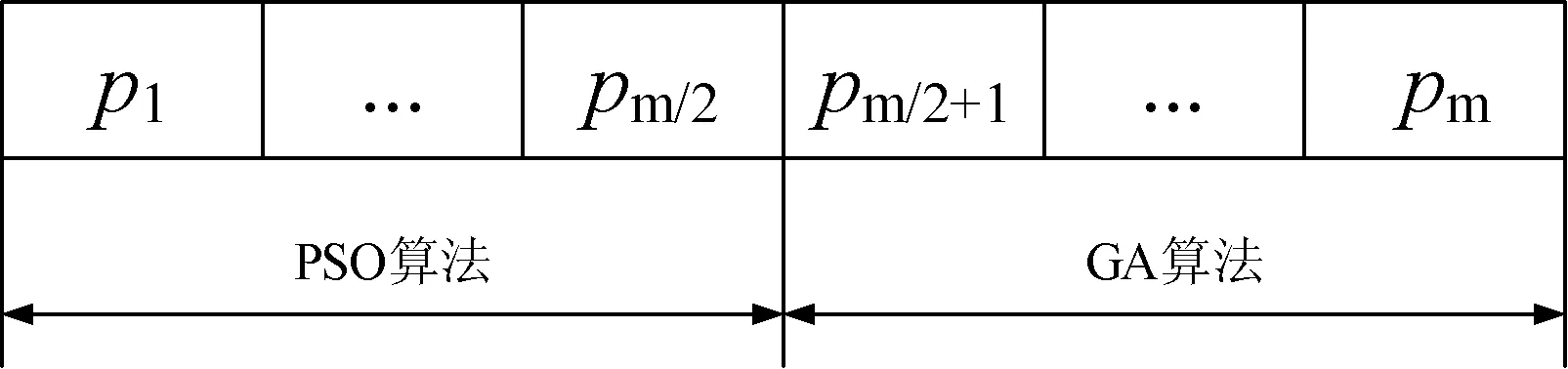
图1 群体划分优化方法的群体排序

PSO算法拥有较好的局部寻优特性以及较快的收敛速度，排序前半部分的个体在整个群体中获得了较好的适应度值，所以局部最优算法PSO作用于这一部分；相反，后半部分的个体适用度较差，只有较小的可能达到好的适应度值，所以为了获得更好的解，使用全局最优算法GA作用于这一部分。

群体划分优化过程如下：

步骤1算法开始时，迭代计数器记为0。初始化群体。

步骤2根据适应度值将群体进行排序。

步骤3目前为止本次迭代和上次迭代中适应度最小的个体作为最优解。

步骤4使用PSO算法作用于图1前半部分的群体，迭代规定的次数。

步骤5使用GA算法作用于图1后半部分的群体，迭代规定的次数。

步骤6迭代计数器加1，如果没有达到终止条件，返回步骤2；否则，算法结束。目前为止具有最好适应度值的个体为所求最优解。

在GAP-RBF算法的基础上，结合本文提出的群体划分优化方法，完整的OGAP-RBF网络学习算法流程见算法1。

算法1基于群体划分优化的GAP-RBF算法

给定网络输入矩阵xn∈Xl和输出矩阵yn∈Y。

1) 计算网络输出f(xn)。

2) 计算增加准则中的相关量εn,en。

3) 应用增加准则判断是否增加隐层神经元：如果增加，设置相应参数αK+1,μK+1,σK+1；否则，用DEKF方法调整距离当前输入最近神经元的参数αnr,μnr,σnr。

4) 检查隐层神经元的删除准则是否满足，如果满足，删除神经元。

5) 重复步骤1到步骤4直到所有新样本顺序地进入网络。

6) 使用已获得的网络权值以及随机值初始化群体。

7) 根据历史样本得到网络输出，根据适应度公式计算个体的适应度值，再对群体进行排序。

8) PSO算法和GA算法分别作用于群体的两部分，得到当前的最优解。

9) 重复步骤7和步骤8直到达到终止条件，获得最优的网络结构。

3 计算机仿真及结果分析

本文采用MATLAB 7.7开发环境，在配置为Intel(R)，Core(TM)i3-3240，CPU 3.40 GHz的Windows 7操作系统上运行。对函数逼近方面的3个Benchmark问题进行实验，将本文提出的算法与其他经典顺序学习算法RAN、RANEKF、MRAN和GAP-RBF在性能上做了比较。这三个问题分别为：(1)波士顿房价预测问题；(2)鲍鱼年龄预测问题；(3)汽车燃油消耗量预测问题。这些数据来自于UCI标准数据库，并具有高维、非均匀分布的特点。通过在三个数据集上的对比实验分析，验证了本文所提算法的有效性和可操作性。

本文用均方根误差RMSE来衡量算法的学习精度，其定义形式为：

(14)

其中n是所求均方根误差的元素个数。训练后的网络结构复杂度通过算法训练网络结束后所确定的隐层神经元个数来衡量，算法的计算速度通过算法学习过程所需要的CPU时间来衡量。

为了实现一个紧凑的RBF网络，各种顺序学习算法都需要一些固定的参数，例如MRAN算法中神经元的增长、剪枝阈值和滑动窗口大小等，但是并没有标准如何正确选择这些参数的值，并且这些值严格依赖于实际的应用。然而，GAP-RBF唯一需要确定的参数只有S(X)，其余参数在大多数情况下是固定的。本文中所需参数的值以及训练测试样本个数都参考文献[8]进行选择。所有算法在三个问题中的通用参数设置如下： εmax=1.15,εmin=0.04,κ=0.10,γ=0.999,emin=0.0001。

对于每个Benchmark问题，为了使输入数据更好地适应于神经网络的学习，防止系统训练过程震荡，输入值和输出值进行归一化。在数据集中随机选取训练集和测试集，每个算法运行50次，并分别计算CPU时间，训练误差，测试误差以及隐层神经元个数的均值和标准偏差进行比较分析。在实验环境和设置参数都相同的条件下，算法RAN、RANEKF、MRAN和GAP-RBF的结果来自文献[8]。实验数据集汇总信息如表1所示。

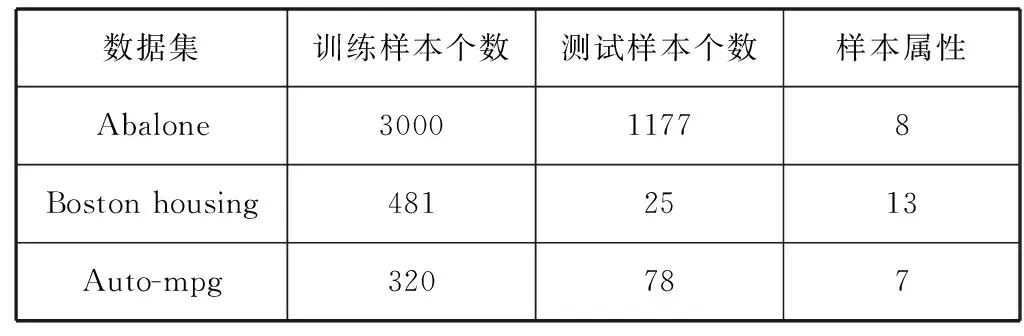
表1 实验数据集

3.1 波士顿房价预测问题

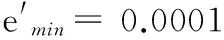
图2给出了各种算法在顺序学习过程中的均方根误差变化曲线，以及OGAP-RBF的顺序学习确定网络结构阶段与其他算法的比较结果。可以看出OGAP-RBF算法在GAP-DEKF构建网络结构的顺序学习阶段，当所有新样本学习过后，可以达到与MRAN和GAP-RBF相当的训练误差。为了进一步提高OGAP-RBF网络的精确度，在本算法中加入了群体划分优化过程，如图3所示，在GAP-DEKF的基础上，将网络的训练误差降低了13%左右。图4给出各算法在训练过程中隐层神经元的更新过程，可以看出，OGAP-RBF可以生成相对较少的隐层神经元。这些图示为在波士顿数据集上的一次典型实验的结果图，在其他数据集上的实验同样有类似的结果。

实验结果如表2所示，将OGAP-RBF与RAN、RANEKF、MRAN和GAP-RBF在算法执行时间、训练误差、测试误差和隐含层神经元个数四个方面进行了比较。可以看出OGAP-RBF与GAP-RBF相比，在相差不多的运算时间和网络结构的前提下，具有更好的训练误差和测试误差。另外三个算法中RANEKF算法虽然训练误差相对较低，但是这些算法所需时间和隐层神经元个数都比较多。所以可以看出在本数据集上，改进算法在学习精度、网络复杂度和计算速度三个方面表现都较好。

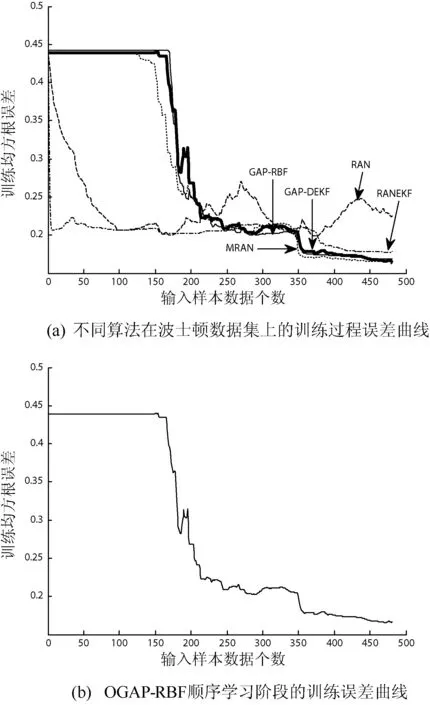
图2 误差曲线

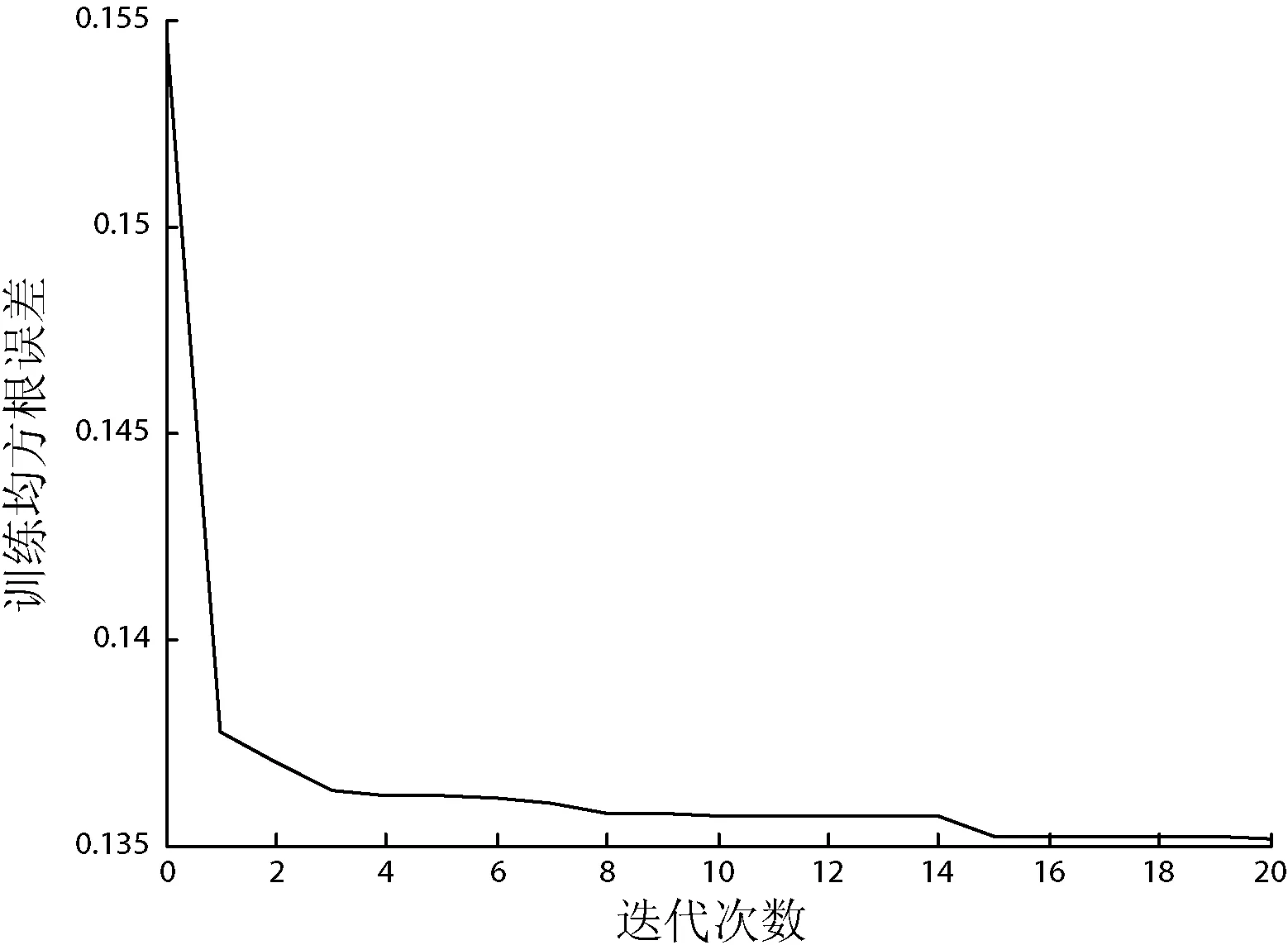
图3 在波士顿数据集上的OGAP-RBF优化过程曲线

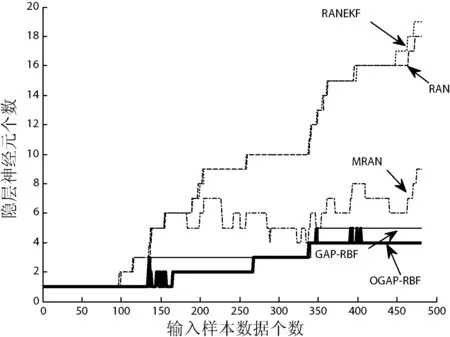
图4 不同算法隐层神经元的更新曲线

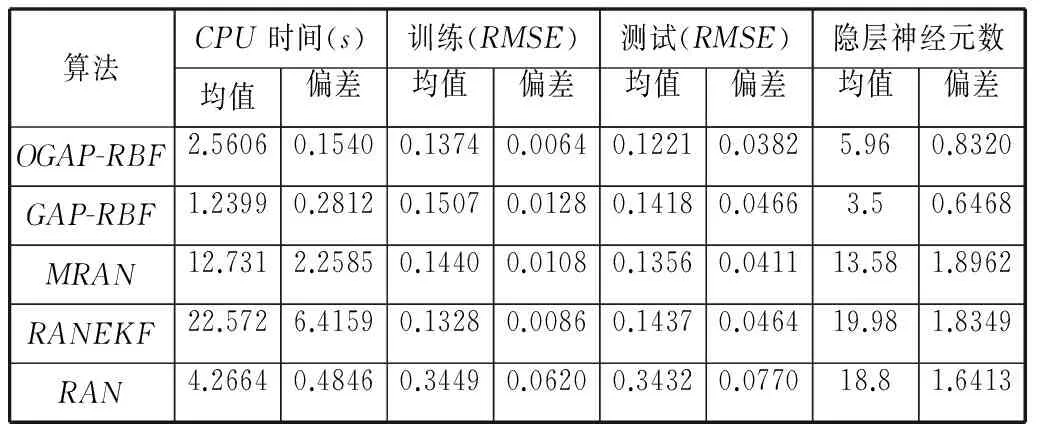
表2 各算法在实际问题Boston Housing应用中的性能比较

3.2 汽车燃油消耗量预测问题

汽车的燃耗问题是用来预测不同类型汽车燃油消耗量的数据库。实验中有398个样本数据，这些样本的输入数据包括车辆的7个属性，样本的输出为汽车的燃油消耗量。

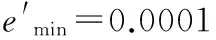
从表3可以看出，OGAP-RBF与GAP-RBF相比，虽然运算时间略有增加，但是在隐层神经元数量相差不多的情况下，训练误差和测试误差明显降低，并且测试误差相对比较稳定。与RAN、RANEKF和MRAN相比，在运算时间基本相当的情况下，OGAP-RBF达到了最低的测试误差和最少的隐层神经元。所以可以看出在本数据集上，改进算法的学习精度和网络结构都具有一定的优越性。

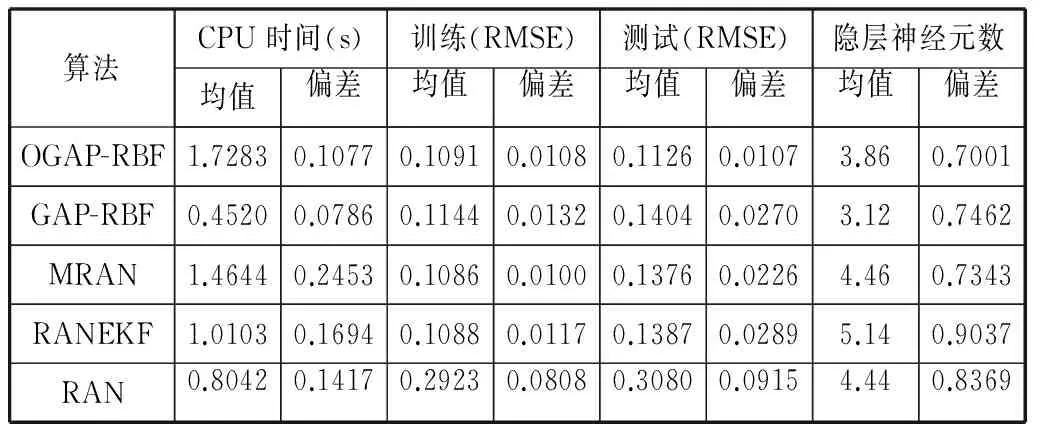
表3 各算法在实际问题Auto-Mpg应用中的性能比较

3.3 鲍鱼年龄预测问题

鲍鱼数据集共有4177个样本数据，是关于鲍鱼年龄预测的数据库。该例中每个数据样本包括9个属性，分别属于不同的年龄阶段。

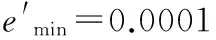
从表4可以看出， OGAP-RBF相比其他算法，运算时间明显降低，这是由于对于数据量较大的数据集，DEKF方法大大降低了计算的复杂度，同时也弥补了群体划分优化带来的额外运算时间。相比GAP-RBF算法，训练误差、测试误差和隐层神经元个数都有一定程度的降低。在所有算法中RANEKF、MRAN和OGAP-RBF都达到了相对较低的测试误差，但是OGAP-RBF算法的运算时间和网络结构都远远优于另外两个算法。所以可以看出在本数据集上，改进算法在各方面都具有一定的优越性。

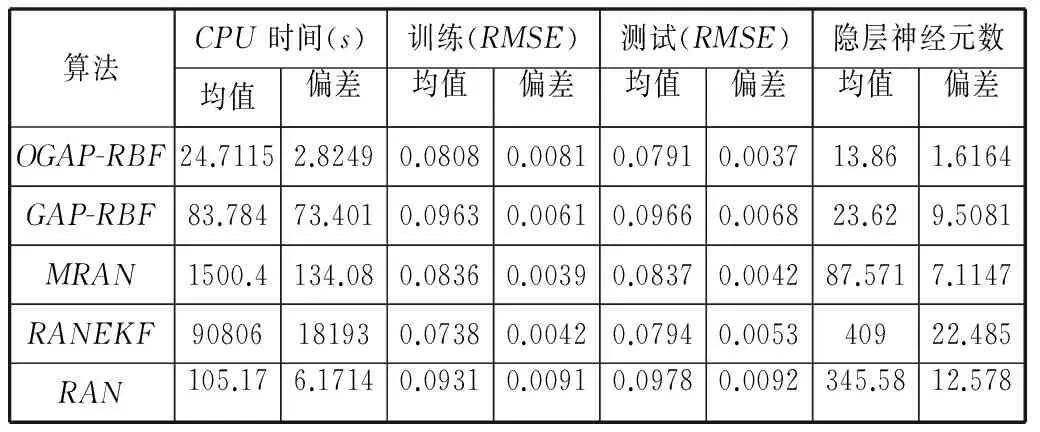
表4 各算法在实际问题Abalone应用中的性能比较

4 结 语

本文提出的基于群体划分优化的GAP-RBF神经网络学习方法，在原有的GAP-RBF做了两点改进：使用DEKF方法来降低网络的计算复杂度和运算时间；利用群体划分方法对网络权值和偏移项进行优化进一步提高网络的学习精度。通过在3个Benchmark问题上与其他学习算法进行比较分析可知，对于不均匀分布的实验数据，OGAP-RBF仍能够获得较好的学习精度，并且在数据量较大的情况下，运算时间和网络结构都远远优于其他算法。可见，改进后的算法提高了网络的泛化能力和处理问题的能力，并建立了性能良好的神经网络模型。

[2] Qiao J F, Han H G. Identification and modeling of nonlinear dynamical systems using a novel self-organizing RBF-based approach[J].Automatica, 2012,48(8):1729-1734.

[3] Chen H, Gong Y, Hong X. Online modeling with tunable RBF network[J].Cybernetics,IEEE Transactions on, 2013,43(3):935-947.

[4] Han H G, Qiao J F, Chen Q L. Model predictive control of dissolved oxygen concentration based on a self-organizing RBF neural network[J].Control Engineering Practice, 2012, 20(4):465-476.

[5] Platt J. A resource-allocating network for function interpolation[J].Neural computation, 1991, 3(2):213-225.

[6] Kadirkamanathan V, Niranjan M. A function estimation approach to sequential learning with neural networks[J].Neural Computation, 1993, 5(6):954-975.

[7] Yingwei L, Sundararajan N, Saratchandran P. A sequential learning scheme for function approximation using minimal radial basis function neural networks[J].Neural computation,1997,9(2):461-478.

[8] Huang G B, Saratchandran P, Sundararajan N. An efficient sequential learning algorithm for growing and pruning RBF (GAP-RBF) networks[J].Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2004,34(6):2284-2292.

[9] Kennedy J, Eberhart R. Particle swarm optimization[C]//Proc IEEE International Conf on Neural Networks. Piscataway: IEEE, 1995:1942-1948.

[10] Holland J H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence[M].MIT Press, 1992.

[11] Puskorius G V, Feldkamp L. Neurocontrol of nonlinear dynamical systems with Kalman filter trained recurrent networks[J].Neural Networks, IEEE Transactions on,1994,5(2):279-297.

[12] Chen Z, Qian P. Application of PSO-RBF neural network in network intrusion detection[C]//Intelligent Information Technology Application, 2009. IITA 2009. Third International Symposium on. IEEE,2009,1:362-364.

[13] Hendtlass T. Restarting Particle Swarm Optimisation for deceptive problems[C]//Evolutionary Computation (CEC), 2012 IEEE Congress on. IEEE, 2012:1-9.

[14] Yourdkhani S. Portfolio Management by using Value at Risk (VaR)(A Comparison between Particle Swarm Optimization and Genetic Algorithms)[J].Life Science Journal, 2014,11(S1):15-26.

[15] Pan Y, Xue W, Zhang Q, et al. A forecasting model of RBF neural network based on genetic algorithms optimization[C]//Natural Computation (ICNC), 2011 Seventh International Conference on. IEEE, 2011,1:48-51.

[16] 严宗光, 邓宇豪. 遗传算法的自适应机制[J].科技资讯,2014(28):192-193.

[17] Yu-liang Q, Hao Z, Daogang P, et al. Fault diagnosis for generator unit based on RBF neural network optimized by GA-PSO[C]//Natural Computation (ICNC), 2012 Eighth International Conference on. IEEE, 2012:233-236.

[18] Zhang R, Huang G B, Sundararajan N, et al. Improved GAP-RBF network for classification problems[J].Neurocomputing, 2007,70(16):3011-3018.

GAP-RBF NEURAL NETWORK LEARNING ALGORITHM BASED ON POPULATION PARTITIONING OPTIMISATION

Bao Qinxin Song Wei

(School of IoT Engineering, Jiangnan University, Wuxi 214122,Jiangsu,China)

Aiming at the problem of traditional GAP-RBF algorithm that its learning accuracy is not high enough, we present in the paper a new GAP-RBF network learning algorithm which is based on population partitioning optimisation. First, for overcoming the large matrix computation problem in traditional GAP-RBF, the proposed algorithm adjusts network parameters with DEKF method; secondly, in order to obtain the network model with higher learning accuracy, the algorithm uses the PSO and GA-based population partitioning optimisation to train the connection weight values of hidden layers and output layers and the bias items. Experimental results indicate that compared with the algorithms such as RAN, RANEKF, MRAN and GAP-RBF, the presented algorithm can obtain a more concise network structure and improves the learning accuracy at the same time.

RBF neural network GAP-RBF algorithm PSO algorithm Genetic algorithm

2015-09-21。物联网技术应用教育部工程研究中心，中央高校基本科研业务费专项资金项目(JUSRP51510)。包沁昕，硕士生，主研领域：神经网络，机器学习。宋威，副教授。

TP183

A

10.3969/j.issn.1000-386x.2016.11.051