快速鲁棒的光学零件表面划痕亚像素检测方法研究

陈少杰 李柏林 刘甲甲 冯河洋

(西南交通大学机械工程学院 四川 成都 610031)



快速鲁棒的光学零件表面划痕亚像素检测方法研究

陈少杰 李柏林 刘甲甲 冯河洋

(西南交通大学机械工程学院 四川 成都 610031)

针对光学零件表面划痕检测精度较低的问题，提出一种多尺度线检测与离散正交多项式曲线拟合相结合的亚像素边缘检测算法。首先，为克服噪声等干扰，基于不同尺度线检测特性，提出改进的多尺度线检测，并通过该方法得到划痕初始轮廓。然后，对边缘点及其邻域在梯度方向上的点进行筛选。最后，利用正交多项式曲线拟合具有模型简单、求解速度较快、拟合精确的特点，对所选取离散点进行曲线拟合，以实现亚像素边缘检测。实验结果表明，该算法检测精度较高，具有较强的鲁棒性，同时更好地适用于屋脊边缘检测；较最小二乘法时间大大降低，且低于较快速的三次样条插值法，平均计算时间比为19.9∶4.73∶1，处理效率显著提高，能够满足工程应用中快速、高精度检测要求。

光学器件 划痕检测 线性检测器 曲线拟合 亚像素边缘检测

0 引 言

光学零件在抛光加工过程中，不可避免地会因抛光磨砂颗粒导致表面存在划痕等缺陷。这些缺陷将会影响元件的正常工作，并影响光学系统的质量。随着机器视觉技术的快速发展，通过高分辨率CCD相机获取疵病图像，采用数字图像处理算法，以实现划痕疵病检测，逐步取代了传统人工检测方法。目前采用的边缘检测、阈值分割等图像处理方法，算法简单、速度快，但对噪声及光照不均等干扰敏感，且只能达到像素级精度[1,2]。现代精密光学加工对表面疵病检测精确度要求提高，像素级精度已经不能满足检测精度的需求，因此需要更高精度的亚像素级的检测算法。

初始边缘的提取是亚像素边缘定位的基础。由于实际采集的图像通常含有较多噪声以及光照不均匀等干扰信息，且划痕边缘与背景对比度不明显，常用的边缘检测算法Sobel、Roberts、Prewitt以及Canny等方法难以提取完整初始轮廓边缘。基于线性检测的边缘检测方法受噪声及光照不均等影响较小，在检测屋脊边缘方面取得一定效果。其最开始是由Ricci等人提出[3]，用于检测视网膜中血管。因其采用单一尺度线性检测器，存在模糊紧邻血管、产生伪边缘等缺陷。Nguyen[4]等人将其推广，构建了多尺度线性检测，在视网膜血管图像分割中取得较好效果；但是其计算模型只是简单地把不同尺度下线检测响应函数进行线性融合，并引入了背景噪声。在此基础上，Hou[5]进一步提出根据不同权重将不同尺度下线检测响应函数进行融合的模型，能够为特征图像提供更多血管信息，但其不同尺度的响应也未能充分利用各尺度线性检测器的特性。本文提出了新的多尺度线性检测器，使其能更好地检测划痕边缘，且适用于常规屋脊边缘检测。目前常用的亚像素精度的检测算法，主要分为插值法[6-8]、矩方法[9-13]和拟合法[14-16]等几类。其中，插值法重复性好，计算量小，但定位精度较低；基于矩的方法，运算复杂度较高，计算量普遍较大。基于高斯曲线拟合方法是对沿梯度方向梯度值进行曲线拟合，模型简单，对于边缘模糊程度不敏感。常用的曲线拟合方法是最小二乘法，其稳定性较好，但计算复杂度高且耗时。

为了实现光学零件表面划痕快速、稳定、精确的边缘检测，本文提出了一种基于改进的多尺度线检测与离散正交多项式曲线拟合相结合的亚像素边缘检测算法。该算法首先通过改进的多尺度线检测得到划痕初始轮廓；然后，筛选边缘点及其邻域在梯度方向上的点，并进行正交多项式曲线拟合，从而实现亚像素边缘检测。通过实验分析和对比，本文改进的多尺度线检测受噪声及光照不均等影响较小，鲁棒性好；基于离散正交多项式曲线拟合的亚像素边缘检测算法快速、易于实现、抗噪声能力较强、定位精度高。

1 基于改进线性检测边缘检测算法

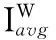
(1)

基础线检测器中，窗口W的尺寸一般选为血管宽度的两倍，以确保当检测窗口的中心位于血管中轴线上时，血管和背景像素数量近似相等，以此区分背景区域线检测器的响应。基础线检测器能很好地处理血管中央反射，受噪声等干扰较小，但是其存在模糊邻近血管、在强边缘处产生伪边缘等缺陷。多尺度线性检测原理是不同尺度下线检测器的响应不同，长尺度线性检测器能够检测大尺寸血管，并且能够处理中央反射；而短尺度检测器能够有效检测细节及邻近的并行血管。基于不同检测器的优点，Nguyen以及Hou分别提出式(2)、式(3)两个不同多尺度线检测模型：

(2)

(3)

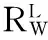
(4)

该模型根据不同尺度响应特性，改进了多尺度的响应权重，使其能更好地发挥不同尺度检测器优势，在避免伪边缘产生的同时，也为划痕边缘提供了更多的细节信息。由于原图含有较多噪声以及光照不均匀等干扰信息，为避免引入原图干扰信息，所以不再加入原图相关信息。

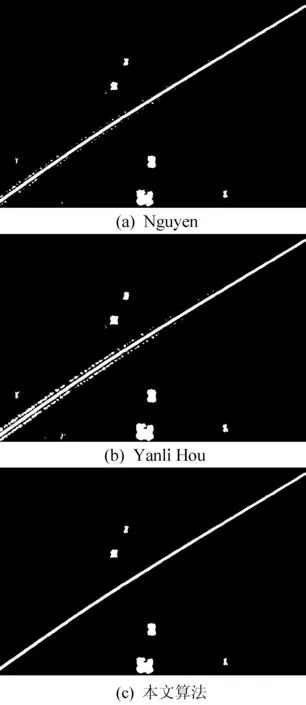
图1 不同算法划痕分割结果

经过多尺度线性检测之后并不能直接把划痕提取出来，其结果代表每个像素属于划痕的可能性。还需要进行后续处理，本文采取自适应阈值分割处理算法。由于划痕宽度集中在7个像素左右，因此设置窗口宽度W为15 个像素。最后得到的图像结果如图1(c)所示。通过图中结果对比可知，本文所提出的多尺度算法在划痕伪边缘以及细节处理方面均比Nguyen与Hou效果好，并且受噪声及光照不均等干扰信息影响较小。

2 亚像素边缘精确定位

边缘附近点(过渡区域)的灰度值通常是连续分布而不是垂直于边缘方向的阶跃分布。根据中心极限定理，沿边缘点梯度方向，灰度变化近似为高斯分布，并且高斯分布的中心是在沿该梯度方向灰度变化最大的地方，即为亚像素边缘位置。因此，只要求得梯度分布曲线的极大值点即可得到亚像素边缘坐标。通过上述划痕检测算法，已经得到像素级边缘点，此时需得到确定高斯曲线的离散点。在实际应用中，取点个数太少会导致定位不准确；反之，会因噪声干扰影响定位精度且增加运算负担。所以本文提出的选取策略过程如下：

(1) 以边缘点为中心，沿边缘的梯度方向在梯度图像中截取一系列像素点的梯度值 g(i),i=1,2,…,n；

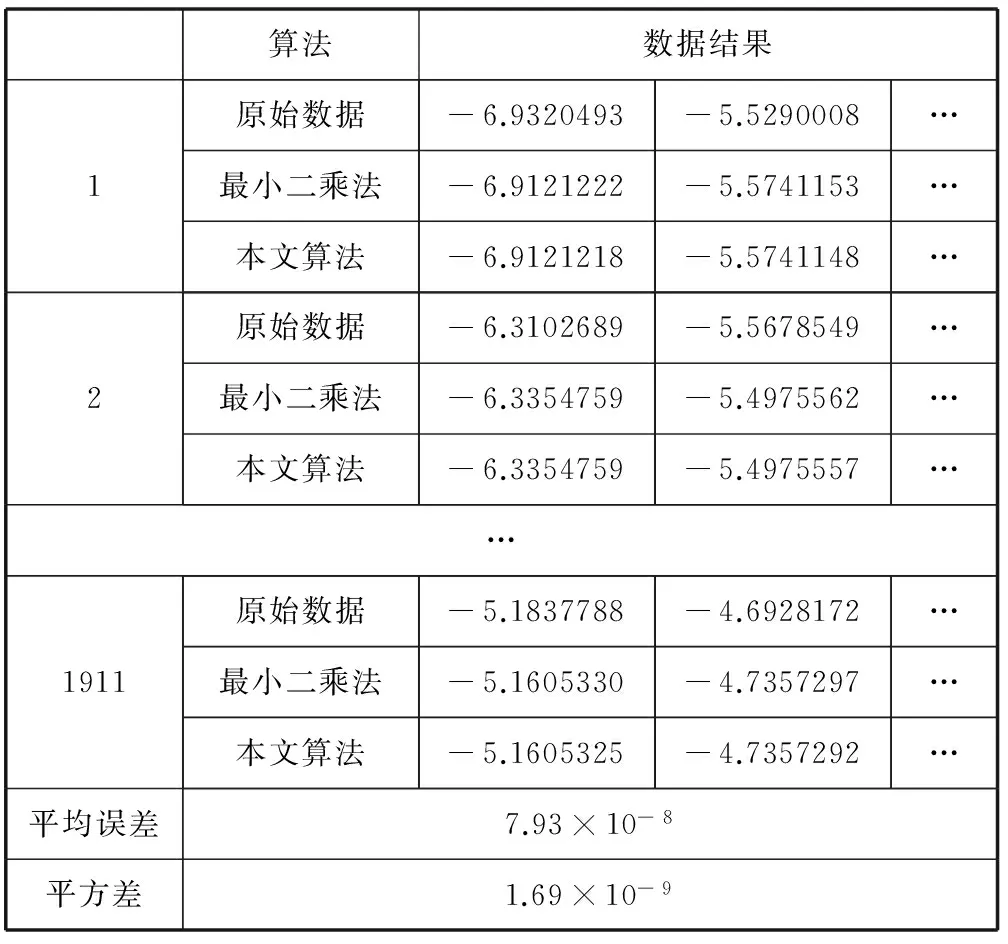
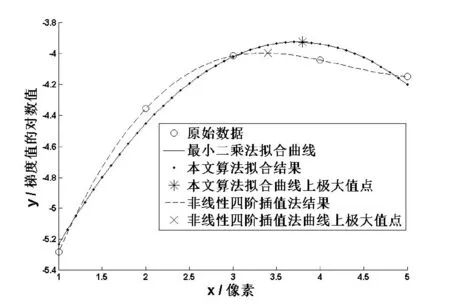
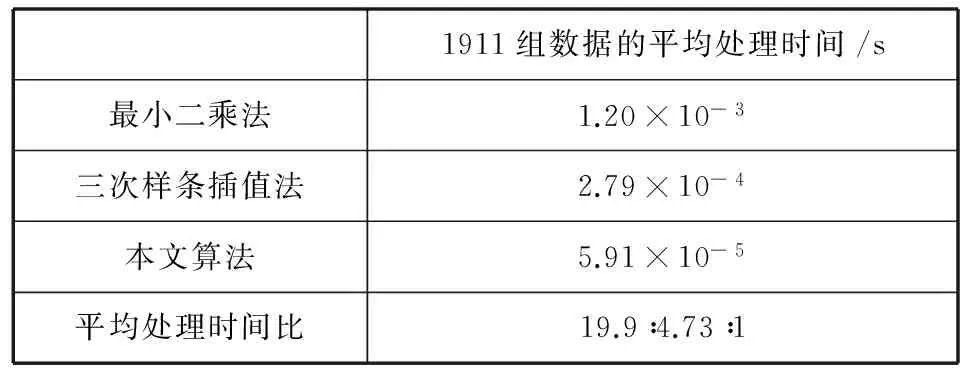
(2) 以g(i)中最大值g(max)位置为分界点，向前后两个方向进行筛选。当g(i)-g(i-1)

由于得到的点的梯度图像是离散的, 直接将这些离散数据拟合成高斯曲线，计算复杂，且难以进行。高斯曲线方程经过等式两边同时取对数后近似为抛物线，且二次曲线是高斯曲线的高次逼近，具有较高的计算精度。通过二次曲线来近似高斯曲线，求出极大值点，即为亚像素边缘点坐标，既能保证误差较小，也能显著提高计算效率。对于二次曲线拟合，常用的方法是最小二乘法，其稳定性较好。但若直接进行最小二乘法求解，计算复杂度高且耗时。为实现快速精确的亚像素边缘检测，本文采用离散正交多项式作曲线最佳拟合[17-19]。

设多项式集合{p0(x),p1(x),…,pn(x)}是关于节点集合{x0,x1,…,xm}的一个正交多项式族。其中pi(x)代表一个i次多项式，一般有n

p0(x)=1

p1(x)=x-α

(5)

pk+1(x)=(x-αk+1)pk(x)-βkpk-1(x) k=1,2,…,n-1

其中pk(x)为最高项系数为1的k次多项式，αk+1、βk+1由{pk(x)}的正交性可得：

(6)

当求解一个n次多项式拟合问题时，可以利用正交多项式pi(x)作为线性组合模型的基函数。本文采用{p0(x),p1(x),p2(x)}作为拟合基底，进行2次正交多项式拟合，则得到拟合多项式函数形式为：

y=a0p0(x)+a1p1(x)+a2p2(x)

(7)

依据线性组合模型的最小二乘拟合问题的求解方法以及正交多项式的定义，可以得到上述拟合问题的最小二乘解对应线性方程组：

(8)

(9)

亚像素边缘点坐标位于曲线的极大值点，通过对拟合曲线求一阶导数即可得到极大值坐标t,于是亚像素边缘坐标为(xs,ys)：

(10)

其中，(xP,yP)为初始像素位置，θ为梯度方向角。由于目标函数是高斯曲线取对数后近似得到，因此进行拟合的值应当用像素梯度值的对数值。

3 实验结果与分析

3.1 像素级边缘检测鲁棒性实验

传统的边缘检测算法中，Canny方法较其他方法抗噪性能好。因此，采用本文算法与Canny算法进行对比实验，实验结果如图2所示。通过对比分析可知，本文提出的多尺度算法，处理得到的划痕经过轮廓提取后边界连续，对噪声的抑制能力较强，受到光照不均等影响较小，处理结果较一般边缘检测方法Canny算法效果更好；且不需要设定阈值，同时适用于一般屋脊边缘检测。

图2 不同算法处理结果

3.2 亚像素级边缘定位精度、鲁棒性以及时间复杂度实验

矩方法因定位精度高和抗噪能力好而被广泛应用，但其定位原理是针对理想阶跃边缘模型，存在原理性误差。且如果考虑模糊后的边缘模型，就会增加模型参数，导致参数求解变得十分困难，不利于实时检测。插值法是对像素点的灰度值[6,7]或灰度值的一阶导数[8]进行插值。其中，基于灰度的三次样条插值方法[7]，根据样条插值原理，得到边缘的连续灰度分布；通过计算样条函数的二阶导数为零点，实现亚像素定位，计算过程简单，运算时间短。文献[6,8]采用非线性四阶插值，以增加图像信息，实现亚像素边缘定位。

针对上述特点，本文采取文献[7,8]中插值法、最小二乘法曲线拟合以及本文算法在定位精度、鲁棒性以及时间复杂度方面进行实验对比验证。

对于曲线拟合，常用的方法是最小二乘法，其稳定性较好。通过对划痕1911个边缘点的数据分别采用最小二乘法和本文算法进行拟合，得到结果如表1所示，其平均误差为7.93×10- 8，平方差为1.69×10- 9。图3中显示了随机抽取一组数据的不同算法的拟合曲线，其中本文算法与最小二乘法拟合曲线重合。这说明了本文算法拟合结果精确且稳定，验证了其有效性及鲁棒性。

表1 不同算法拟合结果对比

图3 不同算法对数据进行处理后曲线图

利用本文算法与样条插值法进行对比实验，其结果在原图中局部显示如图4(a)所示。本文算法得到亚像素边缘点比三次样条插值法稳定，抗噪性较强，精度优于该插值结果。利用本文算法与最小二乘法以及四阶非线性插值法进行对比试验，随机选取一组处理后数据。如图3所示，本文算法与最小二乘法拟合曲线重合，得到的极大值位置(即亚像素边缘点位置)为同一点。虽然该插值法得到曲线更接近原数据，但当原数据受噪声等干扰时，其得到结果也相应地将受到影响；且沿边缘某一梯度方向，梯度值近似为高斯分布，插值法得到的极大值位置与拟合法得到的近似高斯曲线的极大值点有偏差，所以定位结果并不精确。同时综合图4(b)可知，本文算法得到亚像素边缘点比该插值法更接近实际边缘点，精度优于该插值结果。这说明了本文算法的精确性与鲁棒性。

图4 不同算法亚像素边缘检测结果对比

时间复杂度方面，最小二乘法的时间复杂度为O(n4) ；三次样条插值，其时间复杂度为O(n3)；本文算法的时间复杂度为O(n2)。针对1911组数据处理的时间，如表2所示。本文算法时间较最小二乘法时间大大降低，且低于较快速的三次样条插值法，平均计算时间比例为19.9∶4.73∶1，说明了本文算法的有效性。

表2 不同算法处理时间结果对比

4 结 语

本文以光学零件表面划痕疵病图像为例，提出了一种基于改进的多尺度线检测与离散正交多项式曲线拟合相结合的亚像素边缘检测算法。初始边缘提取方面，本文提出的多尺度线检测对于噪声及光照不均等干扰不敏感，得到的边界连续，比Canny算法效果更好，并适用于一般屋脊边缘检测；基于离散正交多项式曲线拟合的亚像素边缘定位方法，很好地解决了最小二乘法复杂且耗时的问题，速度为最小二乘法的19.9倍，且比三次样条插值法速度快；同时拟合精度高，定位较三次样条以及四阶非线性插值法精确，鲁棒性好。实验结果表明，本文提出的方法易于实现、处理效率高、划痕轮廓定位精度较高且稳定。除光学零件图像外，本文所提出的方法对其他类型图像涉及到的屋脊边缘检测也具有很好的处理效果。

[1] Chen X Y,Liu D,Wang S T,et al.Research on digital calibration method for optical surface defect dimension[C]//6th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT 2012).International Society for Optics and Photonics,2012,8417:84173L.

[2] 朱聪,于广婷,李柏林,等.一种新的精密光学镜片表面疵病宽度测量方法[J].计算机应用与软件,2014,31(12):259-261,286.

[3] Ricci E,Perfetti R.Retinal blood vessel segmentation using line operators and support vector classification[J].IEEE Transactions on Medical Imaging,2007,26(10):1357-1365.

[4] Nguyen U T V,Bhuiyan A,Park L A F,et al.An effective retinal blood vessel segmentation method using multi-scale line detection[J].Pattern Recognition,2013,46(3):703-715.

[5] Yanli Hou.Automatic Segmentation of Retinal Blood Vessels Based on Improved Multi-scale Line Detection[J].Journal of Computing Science and Engineering,2014,8(2):119-128.

[6] Hermosilla T,Bermejo E,Balaguer A,et al.Non-linear fourth-order image interpolation for subpixel edge detection and localization[J].Image and Vision Computing,2008,26(9):1240-1248.

[7] 孙秋成,周亚洲,宁闯,等.基于三次样条插值的亚像素边缘检测方法[J].控制工程,2014,21(2):290-293.

[8] 吴鹏,徐洪玲,宋文龙,等.基于非线性四阶图像插值的亚像素边缘检测算法[J].哈尔滨工程大学学报,2015,36(2):243-247.

[9] Da F P,Zhang H.Sub-pixel edge detection based on an improved moment[J].Image and Vision Computing,2010,28(12):1645-1658.

[10] 杨浩,裴蕾,李昌顺.基于Zernike矩亚像素边缘检测的快速算法[J].计算机应用研究,2011,28(11):4380-4382,4385.

[11] 肖锋,郭丽娜.基于降维技术及空间矩的彩色图像亚像素边缘检测[J].计算机应用与软件,2014,31(6):204-207.

[12] Zeng T,Chen S G,Zhang B,et al.A fast subpixel edge detection method for image of micro-part[C]//Fifth International Conference on Machine Vision (ICMV 12). International Society for Optics and Photonics,2013,8783:87831H.

[13] 蔡艳,叶连祥,孙大为,等.基于改进的Zernike矩亚像素边缘提取算法外螺纹非接触测量[J].上海交通大学学报,2014,48(10):1468-1472,1478.

[14] Fabijanska A.Gaussian-based approach to subpixel detection of blurred and unsharp edges[C]//Computer Science and Information Systems (FedCSIS),2014 Federated Conference on.IEEE,2014:641-650.

[15] Flesia A G,Ames G,Bergues G,et al.Sub-pixel straight lines detection for measuring through machine vision[C]//2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings,2014:402-406.

[16] 陈小卫,徐朝辉,郭海涛,等.利用极值梯度的通用亚像素边缘检测方法[J].测绘学报,2014,43(5):500-507.

[17] Li Liwei,Zhang Bing,Gao Lianru,et al.Spectral feature extraction based on Orthogonal Polynomial Function fitting[C]//Pattern Recognition in Remote Sensing (PRRS),2014 8th IAPR Workshop on.IEEE,2014:1-4.

[18] Carley M.Moving least squares via orthogonal polynomials[J].SIAM Journal on Scientific Computing,2010,32(3):1310-1322.

[19] 李建保,张铁,孙宝京,等.基于正交多项式最小二乘分段拟合的气象探测数据处理方法[C]//第23届中国控制与决策会议,2011:838-841.

RESEARCH ON FAST AND ROBUST SUB-PIXEL DETECTION METHOD FOR SCRATCHES ON OPTICAL COMPONENTS

Chen Shaojie Li Bailin Liu Jiajia Feng Heyang

(CollegeofMechanicalEngineering,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)

Aiming at the problem of low precision in scratch detection on optical lens surface, we proposed a sub-pixel edge detection algorithm, which combines the multi-scale line detection and discrete orthogonal polynomial curve fitting. First, to overcome interference of noise, based on the characteristics of line detection in different scales we proposed an improved multi-scale line detection, and obtained initial contour of scratches by this method. Then, we screened the edge points and the points of their neighbourhood on gradient direction. Finally, by making use of the advantages of orthogonal polynomial curve fitting in simple model, fast processing and precise fitting, we fitted the selected discrete points into curve so as to realise the sub-pixel edge detection. Experimental results show that the proposed method has higher accuracy and robustness, and is suitable for roof edge detection better. In terms of processing time, the method is greatly reduced when contrasting with the least square method, and is also faster than cubic spline interpolation method, their average computation time ratios are 1∶19.9∶4.73, the processing efficiency is significantly improved. This method can meet the requirements of fast and high precision detection in engineering applications.

Optical devices Scratch detection Linear detector Curve fitting Sub-pixel edge detection

2015-09-06。四川省科技支撑计划基金项目(2014GZ 0005)。陈少杰，硕士生，主研领域：数字化设计和图像处理。李柏林，教授。刘甲甲，博士生。冯河洋，硕士生。

TP391.41

A

10.3969/j.issn.1000-386x.2016.11.037