基于非局部矩阵填充的文物修复技术研究

杨国亮 鲁海荣 丰义琴 唐 俊

(江西理工大学电气工程与自动化学院 江西 赣州 341000)



基于非局部矩阵填充的文物修复技术研究

杨国亮 鲁海荣 丰义琴 唐 俊

(江西理工大学电气工程与自动化学院 江西 赣州 341000)

文物图像包含了丰富的内容，使用传统偏微分方法很难有效地恢复文物图像。为了有效恢复原图像，提出一种基于非局部矩阵填充的文物修复方法。该算法充分利用图像的冗余信息，在搜索窗口内，通过比较像素点周围一个矩形邻域内的多个像素点的相似性，找到一定数量的相似块转换为列向量，构成相似块组矩阵。由于相似块组矩阵为低秩或者近似低秩的，再通过矩阵填充的原理对损坏像素点进行填充修复。对于文物图像中出现的不同比例像素点丢失、有划痕、有文字破损的修复实验结果表明，该算法能够很好地保留结构细节信息，拥有较好的视觉特性，使目标轮廓边缘特征清晰，有效地恢复出文物图像的原貌，具有良好的修复能力。

矩阵填充 非局部 相似块 低秩

0 引 言

计算机技术的快速发展，促使了信息化时代的加速进步。近年来，随着数字图像应用的日愈广泛，数字图像领域逐渐发展了新型的图像复原技术。

在文物方面，由于历史原因和许多不可抗拒的因素，许多出土的文物会存在物理和化学上的反应，导致出现在我们面前的文物是缺失、不完整的。文物的缺失和不完整，影响着文物的交流与欣赏，更为重要的是没能保护祖先留给我们的历史文化遗产。

长期以来，文物的修复工作主要是由文物工作者进行手工修复。人为手工修复需要工作者具有很高的文物方面的背景知识，凭借自己丰富的经验和感知力对文物进行修复，这种修复方式一旦完成，其修复结果很难再次更改。同时，修复的结果还与修复工作者个人的审美观点和认知有关系，这样，不同的工作者对文物的修复结果也是不一样的。但是，借助数字图像修复技术可以很好地解决这一困境。数字图像修复技术不但可以极大地缩短人工修复周期，而且很大程度上防止了手工修复过程中对文物产生的再次伤害，还能避免人工修复主观因素的影响，尽可能让修复的文物信息更加贴近真实，展现出文物的本来面貌。

近些年来，针对图像的修复问题主要集中在基于偏微分方程PDE、纹理合成方法及其混合的方法。Chan等人提出的整体变分TV(Total Variation)模型也是基于各向异性扩散的，并且它对尖锐的边缘有很好的修复效果。但该方法在图像的平滑区域会产生阶梯效应，不能满足人们的视觉连通性准则。文献[2]提出了基于曲率驱动扩散CDD(Curvature Driven Diffusions)的修复模型，它利用修复点的曲率信息，使用和曲率相关的递增函数，从破损区域边缘向内部修复图像。该方法虽然能够对较大破损区域进行修复，但是容易使图像造成一定程度的模糊。上述两种模型都是利用图像的边界梯度来定义图像的能量函数，从而利用泛函数分析法来求其最小值，所以这两种模型都称为偏微分方程的方法。基于偏微分方程的方法是根据图像中待修复区域的边缘信息，利用热扩散机制沿等照线的方向将已知的信息扩散到待修复的区域中。

随着压缩感知在图像处理领域的发展，近年来，基于稀疏表示的图像修复方法也得到了重视。文献[3]通过输入图像的有效数据和大量样本来训练字典，将字典和数据作为先验知识来对图像进行修复。该方法需要训练大量图像样本，计算效率不高。文献[4]把快速算法与基于稀疏表示的图像修复算法相结合,可以有效地修复小块缺失纹理的区域。文献[5]提出了结构稀疏的图像修复方法，同时考虑了图像的几何结构和纹理信息。然而，上述方法并没有考虑图像的非局部自相似性和充分利用图像的相关信息，对先验信息的表述能力有限。

矩阵填充MC(Matrix Completion)理论[6,7]是继压缩感知、稀疏表示后又一热门研究方向，它旨在将一个低秩的、不完整的矩阵，利用元素间的相关性，完美地恢复出来。而在文物修复中，待修复文物正是由于出现局部的缺失、损坏或者污损，需要使用图像修复技术进行修复。本文充分利用图像的冗余信息，将非局部的思想引入到文物修复中，在搜索窗口内，通过比较像素点周围一个矩形邻域内的多个像素点的相似性，而非单个像素点的相似性，找到最为相似的一定数量的相似块，从而构成相似块组矩阵；再利用矩阵填充的原理对其破损区域进行修复。这样，本文把非局部的思想和矩阵填充的方法联合起来进行文物的修复。

本文算法整体流程如图1所示。

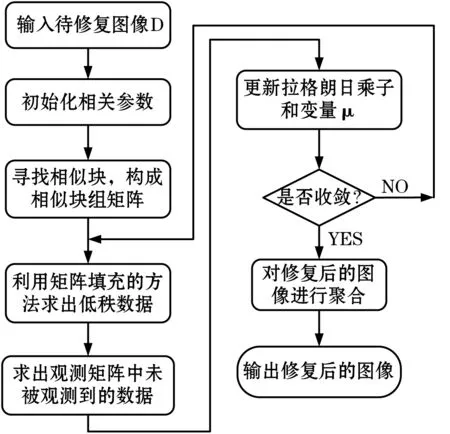
图1 整体算法流程图

1 矩阵填充

矩阵填充技术主要用来解决通过矩阵中的已知数据来恢复其未知或者缺失的数据。它是一个非适定性的问题，如果在没有额外信息调节的约束下，填充的结果有无数多个。然而，当观测矩阵是低秩或者近似低秩时，则可以使观测矩阵精确重构出原始矩阵。

当数据矩阵D中含有丢失元素时，可以通过数据矩阵中低秩结构来恢复出所有元素。假设观测数据矩阵D=m×n，则MC优化模型[7]可以描述为如下问题：

(1)

其中，Ω是矩阵M中被观察到的元素位置的集合，A为待重建的低秩矩阵，PΩ为一线性投影算子，即：

(2)

由于矩阵的秩函数是非连续、非凸的，直接求解秩的最小化问题比较困难。因此，问题是一个NP难问题，无法直接求解。然而Candes等[8]证明，矩阵填充并不是一个病态问题，问题可以通过将秩松弛到矩阵的核范数来近似求解，即得到凸优化问题：

(3)

其中，E表示在观测矩阵D中未知的元素，把它简单设置为0，τ是一个正则化参数。

MC的问题与鲁棒主成分分析RPCA问题比较类似，很自然会考虑使用增广拉格朗日ALM方法来有效求解MC问题，通过构造增广拉格朗日函数对凸优化问题进行求解秩范数。

(4)

然后采用非精确拉格朗日乘子法求解MC问题，在最小化L(A,E,Y)更新E的时候采用PΩ(E)=0这个约束条件。每一步通过最小化该拉格朗日函数，使用交替方向法求解A、E、Y，则式(4)最小值的求解过程可以转换为下列算法流程：

算法1:矩阵填充方法Input:输入观测矩阵1.初始化μ0=0.1,τ=10,tol=10-6 Y0=zeros(size(D))E0=zeros(size(D)),k=0,ρ>12.Whilenotconvergeddo3.(U,S,V)=svd(D-Ek+1μkYk)4.Ak+1=UΘτ/μk(S)VT,其中,Θτ/μk为奇异值收缩算子5.Ek+1=PΩ(D-Ak+1+1μkYk),其中,Ω是矩阵M中未被观察到的元素位置的集合6.Yk+1=Yk+μk(D-Ak+1-Ek+1)7.μk+1=ρμk8.k=k+19.EndwhileOutput:A

2 非局部矩阵填充

在自然图像中，往往会存在这样的一些图像块，虽然它们处在空间域的不同位置，但是它们彼此之间在结构细节部分却存在一定的相似性，我们称这种相似性为非局部结构自相似性。

在图像块中寻找相似块时，如果在整个图像中进行寻找，则算法的计算时间会比较长。这样，考虑到算法性能和耗费时间问题，选择限制搜索范围，改为在一定大小的搜索窗口中进行相似块的寻找。将找到的相似块转化为列向量，组成一个新的相似块组矩阵。由于相似块组的每列都是近似相似的，所以这个相似块组矩阵为低秩或者近似低秩的，则可以利用图像块之间的结构相似性特点，通过矩阵填充的方法对缺失部分数据进行填充。

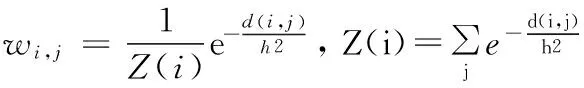
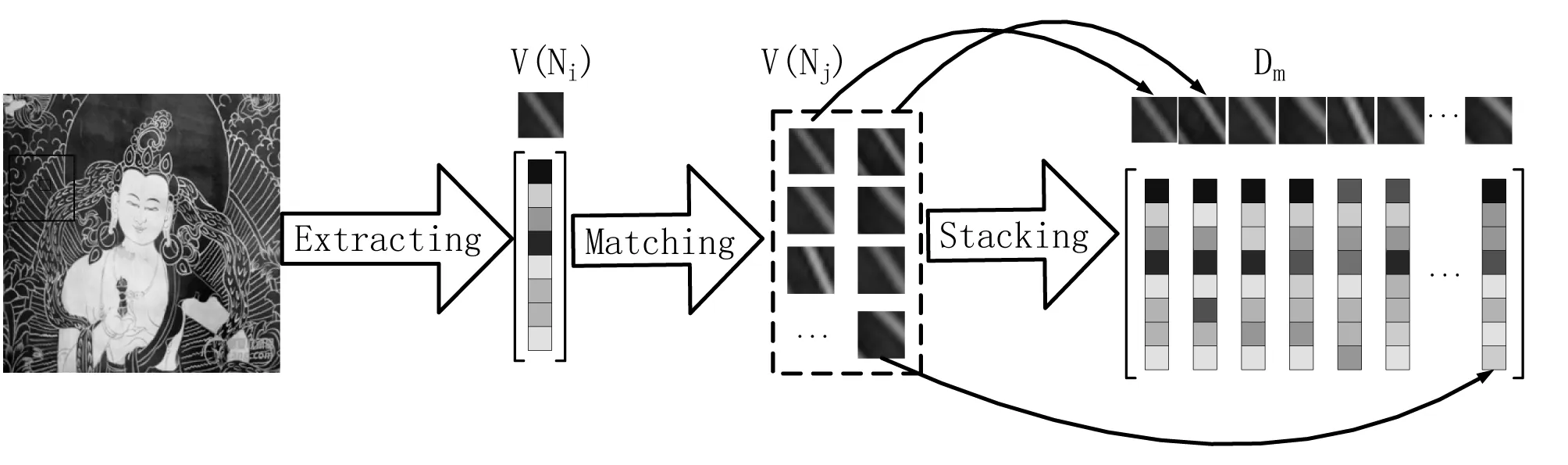
图2 非局部寻找相似块

3 算法实现

对于文物图像的修复可以分为以下四步：

第一步建立搜索窗口。以图像中的某一个像素点为中心建立大小为30×30的搜索窗口。

第二步在当前搜索窗口中计算相似块矩阵。对缺失图像当前窗口进行分块，利用块匹配法对图像块进行相似块匹配，取最为相似的前60个相似块，将匹配后得到的相似块列向量堆叠成图像的相似块组矩阵Dk。

第三步对相似块组矩阵进行矩阵填充。采用矩阵填充的方法修复受损区域，从而得到恢复后的数据矩阵Dk。

第四步聚合。对缺失图像中所有搜索窗口，重复第二步和第三步后得到所有恢复后的图像块矩阵，然后对恢复后的所有图像块矩阵进行聚合就可以获得修复后的图像。

算法流程：

算法2:对输入受损文物图像进行修复1.输入待修复文物图像D;2.建立搜索窗口,在搜索窗口内对Dk分块并进行相似块匹配,得到相似块组矩阵Dk=[Dk1,Dk2,…,Dkm];3.Dk→算法1(对每个相似块组进行算法1操作);4.对恢复出的相似块进行聚合,输出修复后图像。

本文算法的软件编程方式采用Matlab编程，其中较为核心的步骤在于矩阵填充中核范数子问题的求解。本文采用非精确拉格朗日乘子法求解，相比于精确拉格朗日乘子法速度更快。在求解过程中采用奇异值分解，对分解出的特征值收缩，重构后的值即为核范数的解。

核心代码如下：

for k = 1:iterations

%% Step1,update A

V = P.*M-X + (1/mu)*Y;

[U,SigmaY,V] = svd(full(V),‘econ’);

SigmaX = sign(SigmaY).*max(abs(SigmaY)-tau/mu,0);

X2 = U*SigmaX*V′;

A = X2;

%% Step 2,update E

old_E = E;

E = R.*(P.*M-A + (1/mu)*Y);

%% Step 3,update Y,mu

Y = Y + mu*(P.*M-A-E);

mu =ρmu

%% Check stopping criteria

stop_vals(k,1) = norm(P.*M-A-E,‘fro’) / norm(M,‘fro’);

if ( stop_vals(k,1) <= tol)

break;

end

end

4 实验及结果分析

本实验的运行平台为Intel Duo e7500双核处理器、主频为2.93 Ghz、内存为2 GB的台式电脑，使用Windows XP操作系统，通过Matlab R2010a编程实现。

为了衡量经过修复后的图像品质，通常参考峰值信噪比PSNR和结构相似指数SSIM来衡量算法的去噪效果是否令人满意。PSNR值越大，代表失真越少，修复效果越好。SSIM取值范围为0到1之间，其值越大越好，值越大，说明两幅图像的结构越相似。

为了验证本文提出的基于非局部矩阵填充的文物修复方法，采用释迦牟尼的不同画像作为测试图片，图像来源于网络，大小都为256×256。对文物图像进行不同比例的像素丢失修复、有划痕形式的破损修复和文字去除修复这三个方面的实验，并采用传统的TV方法、CDD方法和矩阵填充的方法进行实验对比。

4.1 不同比例的噪声点修复

图 3为原始文物图像丢失10%像素后通过使用不同方法修复得出的结果图。图 3(a)为原始图；图 3(b)丢失10%的像素，纹理信息已被损坏，破损程度较为轻微，PSNR=34.066，SSIM=0.189；图 3(c)为TV方法修复效果，PSNR=29.612，SSIM=0.208；图 3(d)为CDD修复效果图，PSNR=43.295，SSIM=0.976；图 3(e)为MC修复效果图，PSNR=43.923，SSIM=0.975；图 3(f)为本文修复效果图，PSNR=46.241，SSIM=0.990。从实验结果可以看出，本文算法要比TV、CDD和MC方法PSNR值分别高出16.629、2.946和2.318，SSIM值分别高出0.782、0.014和0.015。除了TV方法不能有效修复图像外，其他几种方法修复效果都还不错。然而本文方法PSNR和SSIM值都要比其他几种方法的值要高，能够很好恢复出原始图像。

图3 丢失10%的像素不同修复方法的对比

为了更好体现本文算法的修复效果，再对原始文物图像丢失70%像素做实验进行对比。图 4(a)为原始图；图 4(b)丢失70%的像素，纹理信息损坏严重，破损程度较高，肉眼已无法看清原始图像的轮廓，PSNR=25.614，SSIM=0.032；图 4(c)为TV方法修复效果，PSNR=24.095，SSIM=0.356；图 4(d)为CDD修复效果图，PSNR=33.194，SSIM=0.719；图 4(e)为MC修复效果图，PSNR=33.169，SSIM=0.619；图 4(f)为本文修复效果图，PSNR= 35.682，SSIM=0.819。从实验结果可以看出，TV方法对于不同比例像素点的修复没有效果；在高比例像素点丢失的情况下，本文方法仍然能够有效恢复出原始图像。本文方法的PSNR值要高出CDD、MC方法分别为2.489、2.514，SSIM值要分别高出0.1、0.2。从人眼视觉效果可以看到，本文方法的修复效果图更为平滑，纹理结果保持效果更好；而CDD方法未能有效修复，噪声点较多，边缘还有未能修复的像素点；MC方法也比较模糊，结构纹理丢失严重。从该实验可以看出，经过本文算法的修复，仍能达到人眼可以接受的状态，能够有效修复高比例的像素丢失，可以看到较为清晰的边缘以及丰富的纹理，具有很好的保持结构优势。

图4 丢失70%的像素不同修复方法的对比

4.2 有划痕形式的破损修复

图 5为划痕修复实验。图 5(a)为原图；图 5(b)为有划痕图，上面的划痕损坏严重，纹理信息丢失，视觉效果较差，PSNR=31.014，SSIM=0.277；图 5(c)为TV方法修复效果图，PSNR=31.642，SSIM=0.634；图 5(d)为CDD方法修复效果图，PSNR=38.131，SSIM=0.925；图 5(e)为MC方法修复效果图，PSNR=37.923，SSIM= 0.819；图 5(f)为本文算法，PSNR=41.271，SSIM=0.958。从图中可以看到，TV方法对于这些划痕不能修复，人眼可以很明显地看到还有划痕。相对于TV方法，CDD方法有了很明显的改善，能够很好地去除划痕，但对于边界的修复效果不佳，还能看到很明显的划痕信息。MC方法相对于CDD方法来说效果要差，还有一些很明显的划痕不能去除。而本文算法可以把划痕较好地修复，从而恢复出原图像；对于纹理信息丰富的区域，也能够较好修复划痕，保持原有的结构信息。从实验结果数据来看，本文算法的PSNR和SSIM值也是对比方法中最高的，能够较好地修复划痕。

图5 不同方法划痕修复效果图

4.3 文字去除修复

为了验证本文算法的文字去除性能，同样，我们采用TV、CDD和MC方法进行对比。图 6(a)为原图；图 6(b)为有文字图，文字区域图像的纹理信息被覆盖，破损程度较高，PSNR=37.064，SSIM=0.843；图 6(c)为TV方法修复图，PSNR=42.340，SSIM=0.960；图 6(d)为CDD方法修复图，PSNR=46.595，SSIM=0.986；图 6(e)为MC方法修复图，PSNR=44.877，SSIM=0.968；图 6(f)为本文算法，PSNR=47.668，SSIM=0.991。从实验得到的数据结果中可以看到，本文算法修复图像得到的PSNR和SSIM值在对比方法中是最高的。再通过实验局部放大的结果可以看到，TV方法修复的的结果会模糊化，CDD方法在人头边缘有结构的丢失，使用MC方法在去除文字后有一个很明显的文字轮廓。而本文方法既可以较好去除文字，且能够很好保持图像的边缘结构，视觉效果更好。

图6 文字修复实验对比效果图

5 结 语

本文将非局部均值引入到矩阵填充的修复算法中，充分利用图像的冗余信息，在搜索窗口内寻找相似度较高的相似块，从而转为列向量构成相似块组矩阵，利用矩阵填充的原理来修复图像。通过在不同比例像素的丢失、有划痕和有文字文物图像上分别做实验，并与其他几种算法进行对比，可以看出：本文算法能够最大限度保持图像的基本信息和结构特性，获得较高的PSNR和SSIM值，在一定程度上可以很好保证恢复图像取得较高的视觉质量。同样，本文方法也可以扩展到视频图像中污点的去除，以及旧照片、影视特技应用中。

[1] Chan T F，Shen J H.Mathematical Models For Local Nontexture Inpaintings[J]. SIAM Journal on Applied Mathematics,2002, 62(3):1019-1043.

[2] Chan T F, Shen J H. Nontexture inpainting by curvature-driven diffusions[J]. Journal of Visual Communication and Image Representation, 2001,12(4):436-449.

[3] 李民, 李世华, 乐翔,等. 基于学习字典的图像修复算法[J]. 仪器仪表学报, 2011, 32(9):2041-2048.

[4] Zhao M, Li S T. Hybrid Inpainting Algorithm Based On Sparse Representation And Fast Inpainting Method[J]. International Journal of Digital Content Technology and Its Applications, 2011, 5(7):239-247.

[5] Zongben X, Jian S. Image inpainting by patch propagation using patch sparsity[J]. Image Processing,IEEE Transactions on, 2010, 19(5):1153-1165.

[6] Cai J F, Candès E J, Shen Z W. A Singular Value Thresholding Algorithm for Matrix Completion[J]. SIAM Journal on Optimization, 2010, 20(4):1956-1982.

[7] Lin Z C,Chen M M,Ma Y.The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices[R].UIUC Technical Report UILU-ENG-09-2215,2009.

[8] Candè E J,Recht B. Exact Matrix Completion via Convex Optimization[J]. Foundations of Computational Mathematics, 2009, 9(6):717-772.

[9] Wright J, Ganesh A, Rao S, et al. Robust principal component analysis:Exact recovery of corrupted low-rank matrices via convex optimization[C]//Advances in Neural Information Processing Systems,2009:2080-2088.

[10] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C]//Computer Vision and Pattern Recognition,IEEE Computer Society Conference on. IEEE, 2005,2:60-65.

[11] 李民,程建,李小文,等. 非局部学习字典的图像修复[J]. 电子与信息学报,2011,33(11):2672-2678.

ON CULTURAL RELIC IMAGES RESTORATION TECHNOLOGY BASED ON NON-LOCAL MATRIX COMPLETION

Yang Guoliang Lu Hairong Feng Yiqin Tang Jun

(SchoolofElectricalEngineeringandAutomation,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)

Cultural relic images contain rich contents,and they are difficultly to be restored effectively with traditional partial differential methods.In order to effectively restore original images,we propose a non-local matrix completion-based method for cultural relic image restoration.The method makes full use of the redundant information of image,within the search window and by comparing the similarity of multiple pixels in a rectangular neighbourhood around the pixel,it finds a certain number of similar blocks and converts them to column vector so as to construct the similar block group matrix.Since the obtained similar block group matrix is low rank or near to low rank,we then use matrix completion theory to fill and restore the damaged pixels.It is demonstrated by the restoring experimental results covering the pixels missing in different proportions,scratches and words damages occurred in cultural relic images that the proposed method is able to well preserve the detail information of structure,has good visual characteristics and clear edge features of the target profile.It can effectively recover the original appearance of the cultural relic image with good restoring capability.

Matrix completion Non-local Similar block Low rank

2015-08-31。国家自然科学基金项目(51365017,61305019);江西省科技厅青年科学基金项目(20132bab211032)。杨国亮，副教授，主研领域：模式识别与图像处理，智能控制。鲁海荣,硕士生。丰义琴，硕士生。唐俊，硕士生。

TP391.41

A

10.3969/j.issn.1000-386x.2016.11.030