一类精确修复多个节点的简单再生码
2016-12-26收稿日期20150625国家自然科学基金项目61325005博士生主研领域分布式存储网络编码教授
收稿日期:2015-06-25。国家自然科学基金项目(61325005)。,博士生,主研领域:分布式存储,网络编码。,教授。
一类精确修复多个节点的简单再生码
收稿日期:2015-06-25。国家自然科学基金项目(61325005)。王丽莎,博士生,主研领域:分布式存储,网络编码。唐小虎,教授。
海量数据环境下要求存储系统具有高扩展性、高可靠性和低成本等特点。大规模存储系统的节点因数目巨大而易频繁失效,为保证节点的可用性,系统会利用冗余数据对失效节点进行修复。作为一种新的容错技术,再生码可有效降低分布式存储系统中失效节点修复时需要的下载数据量。基于简单再生码,为分布式存储系统设计一种新的编码方式。它不仅可容忍多个节点同时出错并进行修复,而且编码形式简单并具有较高的码率。
分布式存储系统 精确修复 多节点修复 简单再生码
0 引 言
据国际数据咨询公司(IDC)统计2012年全世界产生的数据量已达到1.8 ZB,全球已进入大数据时代。分布式存储系统通过使用网络中多台机器上的存储设备,把数据分散存储在多个独立的节点上,从而实现对数据的海量存储。分布式存储系统由于单个节点的可靠性不高,需要利用数据冗余技术保证整个系统的鲁棒性,特别地在节点失效时为维持冗余度需要创建新节点代替失效的节点,我们称其为节点修复问题。
在分布式存储系统中,主要有三种节点修复方式: 复制、纠删码和再生码。使用复制和纠删码修复失效节点时,要在系统中传送整个原始信息,才能在新加入的节点上重构出失效的数据块。为减少修复失效节点需要下载的数据量(即修复带宽),Dimakis等[1]将网络编码技术与分布式存储技术结合,提出一种称之为再生码的新的编码策略。对于(n;k;d)——再生码,它需要满足: (1) 是(n;k)——MDS 码; (2) 当一个节点失效时,新节点可以连接剩下的n-1个节点中任意d(d≥k)个恢复该节点的数据。文献[1]中利用网络信息流图理论给出了节点存储容量和修复带宽之间的理论界,并基于随机网络编码技术构造出达到理论界的最佳再生码。其中最小存储再生码MSR Code(Minimum Storage Regenerating Code)和最小带宽再生码MBR Code(Minimum Bandwidth Regenerating Code)因分别具有最小存储量和最小的修复带宽故而最为重要。再生码修复失效节点时,恢复出的数据和原节点存储的数据可能不一样,这种修复模式被称为功能修复。而精确修复因能确切地恢复出失效节点的数据,更符合实际系统的需要,所以更具研究意义。目前为止,基于完全图或干扰对齐技术构造得到的精确修复的MBR和MSR码的编码策略日趋完善[2-4]。最一般的编码方法是Rashmi等在文献[4]中利用矩阵乘积的形式给出的, 但是它们的码率都不高。
上面修复机制的研究都是基于单节点失效情形给出的编码方案,然而在实际的分布式存储系统中多节点同时失效的问题也很常见。针对多节点修复,目前有两种解决方案: 第一种是将多节点修复过程转换为多个独立的串行的单次修复,此时系统中所使用的(n;k;d)——再生码只要满足n≥d+r,即可依次修复出r个失效的节点。事实上在实际修复机制下,修复过程中需要修复的新节点之间也可以进行数据传输,以进一步减少修复带宽,这种方式被称为多节点合作修复[5]。Shum等在文献[6]中确定了节点存储容量和修复带宽的理论关系,并依此给出了对应的最小存储合作再生码MSCR Code(Minimum Storage Cooperate Regenerating Code)和最小带宽合作再生码MBCR Code(Minimum Bandwidth Cooperate Regenerating Code)的参数。对此,Wang等[7]构造出了任意参数(n,k,d,r)下的非线性MBCR码,Chen等[8]给出了参数为(n=2k;k)的MSCR码,但精确合作修复的再生码构造方法还很少。在这些已知的编码体制的基础上,近年来人们更多的关注于新的编码形式[9-15]。
2012年,Papailiopoulos等[9]利用MDS码构造了一类简单再生码。该编码方式把信息重建和节点修复这两个问题分离,通过简单的异或运算来精确修复系统中单个失效的节点。此外,其节点存储量也与再生码要求的存储最小理论值接近。而对于其它高码率的编码构造方案[13-15]节点数据存储量为(n-k)的幂指数,这极大地增加了系统的复杂性。本文中,基于简单再生码,我们提出一种新的编码方式,可容忍多个节点同时失效并通过简单的计算进行修复。同简单再生码一样,这种编码形式有较高的码率和较小的节点存储。
1 预备知识
本文首先给出简单再生码[9]的具体构造: 设文件W大小为M=kf,将其分成f部分:W=[W(1)…W(f)],这里W(i)∈F1×k,i∈{1,…,f},F是一充分大的素域。此时W(i)可以看成是一个长为k的向量,利用一个(n;k)——MDS 码G∈Fk×n分别对其编码,形成f个长为n的编码向量x(i)= (x0(i),…,xn-1(i)) =W(i)G,其中i∈{1,…,f}。于是根据MDS码的性质可知,x(i)中的任意k个数据组可以恢复W(i),i∈{1,…,f}。接着利用:
(1)
生成n个校验数据,最后将这(f+1)n组数据放入表1所示的n个节点中,注意本文涉及节点序号的运算是模n的。

表1 节点数据存储方式
上述简单再生码可以容忍任意n-k个节点的错误,并且能够使用简单的异或运算进行节点的修复,详见文献[9]。此外,在修复任意失效节点时需要连接的剩余节点数为min(2f,n-1)。但是,这种简单再生码仅能每次修复一个失效的节点。本文接下来的部分,针对能精确修复多个失效节点的简单再生码进行研究。
2 能够精确修复r=2的错误再生码
本节中,我们改进简单再生码使其可以修复r=2的错误。
2.1 编码构造
我们保持其他数据不变,仅修改式(1)中的n个校验数据:
(2)
这里j=0,1,2,…,n-1,要求n≥3f+1且n-(f+1)≥d≥f。由于仅改变校验数据,所以任意选取的k个节点中,每行包含的k个编码数据可恢复W(i),i∈{1,…,f},f行即可重构出原始文件。
2.2 修复方式
我们具体地给出一般的f,d=f时修复r=2的错误方案,对于其他的d,其修复方法与过程类似。



引理1若如下形式的编码数据同时失效:
则只需下载3f个数据即可完成修复。
(3)
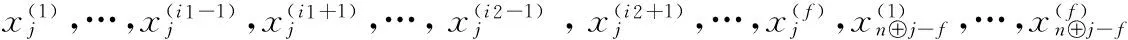
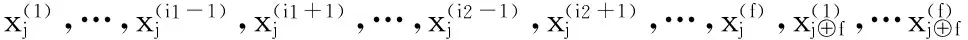
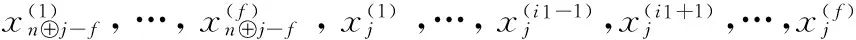
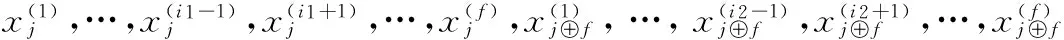
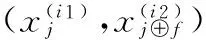
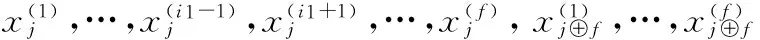
利用引理1,接下来我们根据修复类型详细分析编码方式(2)下r=2的错误修复过程:

表2 情形(Ⅰ)需修复的数据


表3 情形(Ⅱ)需修复的数据

表4 情形(III)需修复的数据


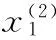
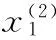

通过上面对修复类型的分析,我们将可以修复的节点对情形总结如表5所示。

表5 各修复情形所对应的节点对
为避免重复,我们对节点个数n的不同进行如下讨论。注意到如下主要针对n的取值不同来分类,与上述情形I-III分类不同,主要目的是为避免重复修复节点对。
2.2.1 n=3f+1时的修复
当n=3f+1时,依据表5容易验证,只需讨论上述三种修复情况,即可修复出节点对(1,j),j=2,3,…,n。
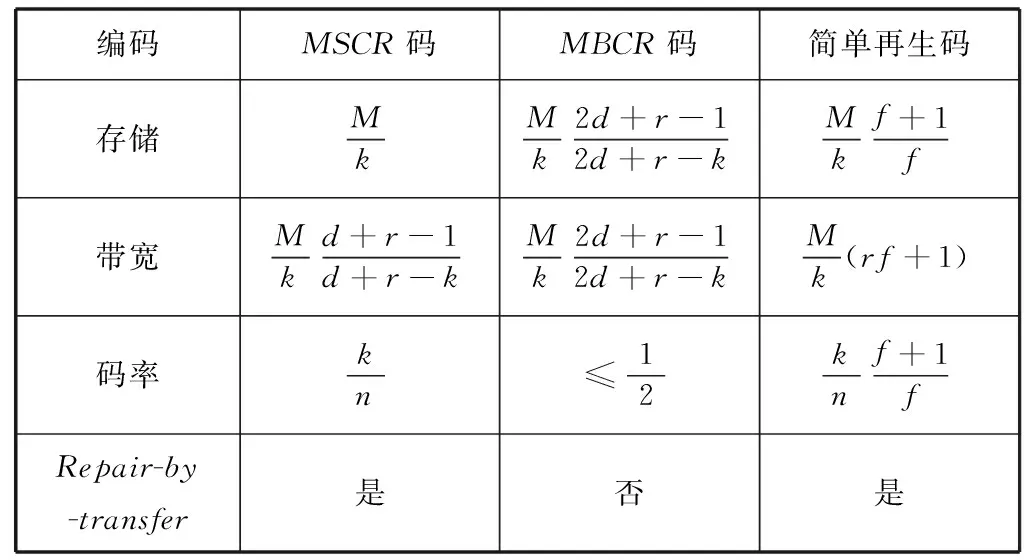
2.2.2 3f+1 当3f+1 (IV) 设N=3f+1+j,j=1,2,…,f-1。节点对(1,f+1+t),t=1,2,…,j失效,我们需要修复数据如表6所示。 表6 情形(IV)需修复的数据 此时根据上面的讨论,我们得到如下节点对的修复情形(见表7)。 表7 修复情形(IV)对应的节点对 2.2.3 n≥4f+1时的修复 当n≥4f+1时,对于修复情形(IV) ,取j=f-1,可以修复节点对(1,f+2),…,(1,2f)。再结合表2,那么只需考虑节点对(1,2f+2),… ,(1,n-2f)的修复即可。 (V) 节点对(1,j),2f+2≤j≤n-2f失效。 此时,我们得到如下节点对的修复情形(见表8)。 表8 修复情形(V)对应的节点对 通过上面的分类可知,最多通过上述五种情况的讨论即可修复节点对(1,j),2≤j≤n。根据节点数据放置的对称性,可类似的修复任意的节点对,从而式(2)的编码方式可容忍r=2的节点失效。 实例:当参数f=3时,取n=10,12,15,上述五种修复情形可修复的节点对分别如表9所示。 表9 各修复情形及所修复节点对实例 2.3 修复带宽 修复r=2的失效节点,需要修复2f个编码数据和2个校验数据。根据上节的讨论,我们得到修复2f个编码数据需要的下载量如表10所示。 表10 各修复情形所需下载量 修复校验数据时,可以重复利用下载的数据,或是利用已修复的编码数据,所以需要再下载的数据量最多为2f。因此结合表10可知,修复r=2的失效节点需要的带宽最多为4f2+2f=2f(2f+1),那么相应的修复一个节点的修复带宽为f×(2f+1)。 注4对于n=3f+1,d=f按照上述的方式进行编码,经验证可以同时修复r=2的失效节点的数据。选取N=(3f+1)m个节点,并平均分成m份,每份含有3f+1个节点。对n=3f+1,d=f的编码形式复制到这m份中,那么我们就得到了一个新的再生码。这种新的再生码同样可以同时修复r=2的失效节点的数据, 并且修复数据需要连接的节点数(Repair Locality)可以只有3f+1个。 3.1 编码构造和相关性能 基于r=2的编码构造方式,我们把它扩展成可容忍任意r个节点同时失效的编码形式。此时数据应当进行r次校验,具体的校验数据的形式为: (4) 这里要求节点个数n≥(2r-1)f+1,才能从剩余可用的节点上下载的数据,修复出失效的数据。因此关于任意r个节点错误的修复过程虽然更复杂,需要讨论的情况更多,但是总能够找到相应存活的数据进行修复,在此我们省略其具体过程。 当f无限增大时,可达到任意高的码率: 3.2 存储代价及相关性能的比较 在表11中,给出了可以修复多个失效节点的编码:MSCR码,MBCR码和改造的简单再生码之间的比较。主要涉及以下四个参数:每个节点的存储代价;修复任意r个失效节点时,每个节点需要的带宽;编码率;Repair-by-transfer性质,即可以直接从剩余节点下载数据进行修复。由表11可知,改造的简单再生码的存储和修复带宽只与f有关,并且当f越大时,与MSCR码的存储最小理论值和码率越接近。而现有的MSCR码的编码策略中,要求节点数据存储量为(n-k)的幂指数,这极大地增加了系统的复杂性,改造的简单再生码却可以存储多项式函数。对于修复带宽,相比于利用拉格朗日插值法需运算而构造的MBCR码,改造的简单再生码在修复数据时,可以直接从剩余节点下载数据,运算简单并且可靠型强。所以,改造的简单再生码与其他可以修复多个失效节点的编码相比,花费较小的存储代价,且达到简单的修复运算性能,可适用于分布式存储系统中。 表11 与MSCR、MBCR码的参数比较 本文基于文献[9]中单节点失效的情形,通过对校验节点的数据进行适当的修改,使其可以对多个节点同时失效进行精确修复。本文具体给出了r=2的失效节点的详细修复过程,并讨论了其修复带宽。通过对本文所生成的简单再生码在存储代价和相关性能上的分析,可知简单再生码具有Repair-by-transfer性质,即可以直接从剩余节点下载数据进行修复,码率较高,并且简单再生码的编码方式简单,因此具有一定的优越性。 [1] Dimakis A G, Godfrey P B, Wu Y, et al. Network coding for distributed storage systems[J].IEEE Transactions on Information Theory, 2010, 56(9):4539-4551. [2] Suh C, Ramchandran K. Exact-repair MDS codes for distributed storage using interference alignment[C]//IEEE International Symposium on Information Theory, ISIT 2010, Austin, Texas, USA,2010:161-165. [3] Shah N B, Rashmi K V, Kumar P V, et al. Interference alignment in regenerating codes for distributed storage: Necessity and code constructions[J]. IEEE Transactions on Information Theory,2012,58(4):2134-2158. [4] Rashmi K V, Shah N B, Kumar P V. Optimal exact-regenerating codes for distributed storage at the MSR and MBR points via a product-matrix construction[J].IEEE Transactions on Information Theory, 2011,57(8):5227-5239. [5] Hu Y, Xu Y, Wang X, et al. Cooperative recovery of distributed storage systems from multiple losses with network coding[J].IEEE Journal on Selected Areas in Communications, 2010,28(2):268-276. [6] Shum K W, Hu Y. Cooperative regenerating codes[J].IEEE Transactions on Information Theory, 2013,59(11):7229-7258. [7] Wang A, Zhang Z. Exact cooperative regenerating codes with minimum-repair-bandwidth for distributed storage[C]//Proceedings of IEEE INFOCOM,2013:400-404. [8] Chen J, Shum K W. Repairing multiple failures in the Suh-Ramchandran regenerating codes[C]//IEEE International Symposium on Information Theory,2013:1441-1445. [9] Papailiopoulos D S, Luo J, Dimakis A G, et al. Simple regenerating codes: Network coding for cloud storage[C]//Proceedings of the IEEE INFOCOM 2012, Orlando, FL, USA, 2012:2801-2805. [10] 李小兵, 许胤龙, 林一施,等. X再生码:一类适用于云存储的准确修复编码[J]. 计算机应用与软件, 2014,31(8):241-244,248. [11] Shah N B. On Minimizing Data-Read and Download for Storage-Node Recovery[J].IEEE Communications Letters, 2013,17(5):964-967. [12] Ernvall T. Codes between MBR and MSR points with exact repair property[J].IEEE Transactions on Information Theory,2014,60(11):6993-7005. [13] Papailiopoulos D S, Dimakis A G, Cadambe V R. Repair Optimal Erasure Codes through Hadamard Designs[J].Information Theory IEEE Transactions on,2013,59(5):3021-3037. [14] Tamo I, Wang Z, Bruck J. Zigzag Codes: MDS Array Codes with Optimal Rebuilding[J].IEEE Transactions on Information Theory, 2013,59(3):1597-1616. [15] Li J, Tang X, Parampalli U. A framework of constructions of minimal storage regenerating codes with the optimal access/update property[J].IEEE Transactions on Information Theory, 2015,61(4):1920-1932. 王丽莎 唐小虎 (西南交通大学信息科学与技术学院 四川 成都 611756) A CLASS OF SIMPLE REGENERATING CODES CAPABLE OF EXACT MULTI-NODE REPAIR Wang Lisha Tang Xiaohu (SchoolofInformationScienceandTechnology,SouthwestJiaotongUniversity,Chengdu611756,Sichuan,China) Massive data environment requires the storage system with the characteristics such as high scalability, high reliability and low price, etc. However, the nodes in large-scale storage system will frequently failure due to too huge in number. In order to ensure the usability of nodes, the system will use redundancy data to repair the failure nodes. As a new fault-tolerant technology, regenerating code can effectively reduce the amount of the download data required when repairing the failure nodes in distributed storage system. In this paper, we design a new encoding mode for distributed storage system based on simple regenerating codes. This mode can not only tolerates the simultaneous errors of multiple nodes and repairs them, but also has simple encoding form and achieves higher code rate. Distributed storage system Exact repair Multi-node repair Simple regenerating codes TP302.8 A 10.3969/j.issn.1000-386x.2016.11.003


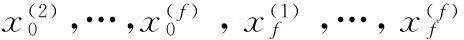



3 能够精确修复r个错误的的再生码
4 结 语
