锥角变化对旋流除砂性能影响的数值模拟*

张晓光 赵立新 徐保蕊 蒋明虎 邓 鑫

(1. 东北石油大学机械科学与工程学院；2. 中国石油天然气管道工程有限公司)

锥角变化对旋流除砂性能影响的数值模拟*

张晓光**1赵立新1徐保蕊1蒋明虎1邓 鑫2

(1. 东北石油大学机械科学与工程学院；2. 中国石油天然气管道工程有限公司)

针对在油田开展采出液除砂的必要性进行了介绍，对所研究的除砂型旋流器结构和基本原理进行了说明。利用数值模拟软件Fluent，将某油田现场采出液作为分离对象，对主直径为56mm的除砂旋流器进行变锥角结构数值模拟研究。得出不同锥角结构旋流器的速度场、压力降和砂相体积分数分布的变化规律，并对不同锥角结构旋流器的除砂分离效率进行了对比。研究表明：当锥角为5°时，旋流器内部产生的切向速度最大，底流出口砂相体积分数分布最高，但也伴随着较大的压力降，所完成的砂相分离效率最高为96.30%。

旋流器 锥角 除砂 分离性能 数值模拟

随着油井开采时间的延长，油井采出液中含砂量越来越高，甚至一些油井从投产时就存在严重的采出液含砂问题[1]。现有的沉降清砂方法周期长、占地面积大、所耗费成本较高，已不能适应油井采出液产液量逐年上升、含砂量逐年增加的现状。近年来不进罐清砂技术(如旋流分离)在石油工业中应用广泛。除砂用水力旋流器是利用固液两相介质间的密度差将分散相——砂相从连续相——液相中分离出来的一种技术方法，具有装置紧凑、占地面积小、分离周期短、处理量调节范围大及设备投资成本小等优点。

除砂用水力旋流器是一种应用广泛的分离设备，不仅可用于油田除砂、脱泥，还可以用于矿场分级分离、洗涤等。研究表明旋流器锥角结构参数对旋流器的分离性能影响较大，但由于旋流器处理介质不同、主要结构形式不同，锥角变化对旋流器分离性能的影响规律也不尽相同[2，3]。越来越多的研究表明，利用数值模拟方法研究旋流器内分离流场的方法具有成本低、速度快的优点，模拟结果确实可反映旋流器内流体的流动规律[4，5]。

油井采出液除砂对于旋流器的要求主要是提高旋流器底流口排砂浓度，笔者结合油田采出液含砂的实际情况，借助于计算流体动力学CFD数值模拟方法，研究分析了一种单锥形水力旋流器的锥角变化对旋流器速度场、压力降、底流含砂浓度和除砂分离效率的影响规律，给出了适用于油井采出液除砂旋流器的最佳锥角。

1 旋流分离器结构分析

旋流器的工作原理是运用离心作用进行液固两相分离，水力旋流器本身无任何运动部件，由待分离的固液两相混合液以一定的压力从水力旋流器入口切向进入，产生强烈旋转运动，由于固液两相的密度差，两相所受的离心力、向心浮力和流体曳力的大小不同，大部分的重质相(固相)经由旋流器底流出口排出，而轻质相(液相)则由溢流出口排出，从而达到固液两相分离的目的[6]。

旋流器通常由入口、旋流腔、锥段、溢流出口和底流出口组成(图1)[7]，主要结构参数包括主直径D1、锥角α、入口当量直径di、旋流腔长度L1、溢流管直径Do、溢流管伸入长度Lo及底流管直径Du等，其中，主直径与锥角两个参数最为重要，这是因为旋流体长度由D1与α决定，其他结构参数也均与D1成一定比例关系。入口形式选择切向双入口矩形结构，其当量水力直径计算值为主直径的0.22倍，矩形入口断面与旋流腔壁面相切，能较好地消除来液短路的死区，减弱可能出现的循环流，使入口来液液流更稳定。其他主要参数设置分别为：Lo=0.714D1、Do=0.357D1、L1=D1。

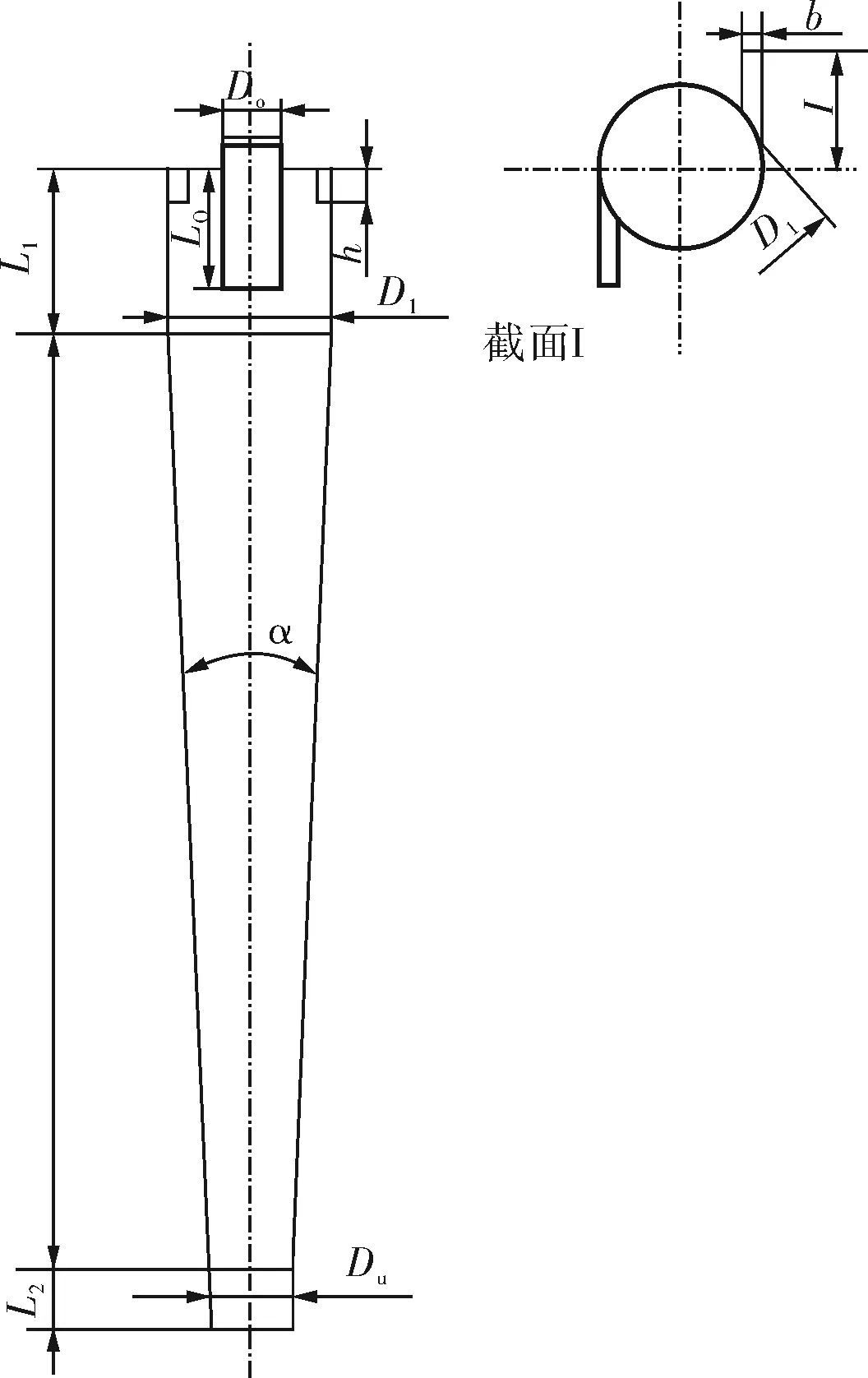
图1 旋流器结构示意图

图2为不同锥角结构旋流器的结构形式对比图，变换锥角主要对旋流器锥段的长度产生影响，而旋流器旋流腔、溢流管段、底流管段的结构参数不变。模拟结构确定旋流器主直径为D1=56mm，用Hy-α5、Hy-α8和Hy-α10分别代表旋流器锥角为5、8、10°的结构，其锥段计算长度分别为5.71D1、3.58D1和2.86D1。

图2 不同锥角水力旋流器结构形式对比

2 参数设置与网格划分

2.1介质物性参数与初始条件设置

进行模拟计算时，对应介质的物性参数为：油相密度870kg/m3，动力粘度0.046 1kg/(m·s)，油相粒径0.09mm；水的密度998.2kg/m3，动力粘度1.003g/(m·s)；砂的密度2 500kg/m3，动力粘度1.72×10-5kg/(m·s)，砂平均粒径0.09mm。

根据油田某站实际情况，初始模拟计算边界条件设置为：入口流量4m3/h，入口油相体积分数为7.9%，入口含砂1.5%，溢流分流比为80%；入口法向速度分量为9.26m/s，其他两个方向的速度分量为零；溢流出口和底流出口均设定为自由出口。

2.2网格划分

利用CFD前处理软件Gambit进行模型构建和网格划分，划分网格如图3所示，所划分网格基本采用六面体结构性网格形式，不同锥角结构形式旋流器的入口段、旋流腔段、溢流出口管段和底流出口管段网格划分一致，对于锥段部分依照等间距划分网格方法，使得不同锥角旋流器的锥段部分网格划分密度一致。同时进行网格独立性检验[8]，分别划分不同数量的网格水平，对比不同网格划分水平对底流出口含砂体积分数变化的影响，结果显示网格数为281 200时，底流出口砂相体积分数分布基本不随网格数的增多而变化。

图3 旋流器模型建立和网格划分

3 速度场影响分析

主要对旋流器内速度场、压力降和固相体积分数分布进行分析。

旋流器内液流为三维湍流流动，其速度场用圆柱坐标系来表示，分为3个分速度：切向速度vt、轴向速度va和径向速度vr。由于切向速度在数值上远大于轴向速度和径向速度分量，因此分析中暂忽略轴向和径向两个速度分量，主要针对切向速度进行重点研究[9～12]。

vt是旋流器内速度场中最重要的一个速度分量，vt的大小决定着旋流器中产生的离心加速度和离心力的大小，也是固液分离中固相颗粒分离的先决条件。由于旋流器为轴对称结构，且入口采用对称双入口结构形式，因此选取旋流腔与锥段连接处横截面I作为不同锥角结构旋流器内部速度场的对比截面，该截面上的速度变化直接受到旋流器锥段变化的影响，更能体现旋流器锥角变化对分离器内部流体流动的影响规律。

对比截面I上，不同锥角结构旋流器的vt分布对比曲线图如图4所示，由图可见，截面I上切向速度呈周向对称分布，3种锥角结构旋流器的vt变化趋势基本一致：中心处速度均为零；随半径的增加，切向速度也逐渐增加，且存在一个最大切向速度点vtmax，在该点处随着半径的进一步增加，旋流器vt逐渐减小，在边壁处的切向速度减小为零，因此以最大切向速度为界，使得旋流器内部分为内涡流区和外涡流区两个区域，由于溢流分流比设置为80%，明显高于底流分流比，可以看出内涡流区也明显大于外涡流区。

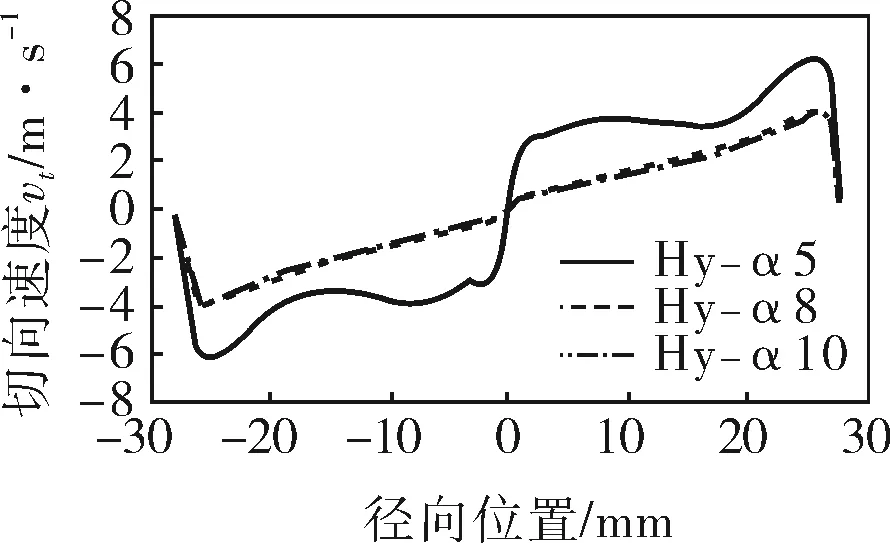
图4 切向速度分布对比

由图4也可看出3种锥角结构旋流器的切向速度变化规律的不同：在径向位置(0～3mm)范围内，Hy-α5旋流器变化梯度最大，随锥角的增加，该区域的切向速度变化梯度逐渐减小，且Hy-α8与Hy-α10两种锥角结构旋流器的切向速度梯度变化差异不大；径向位置(3～20mm)范围内，Hy-α5旋流器的切向速度在一定范围内基本不变，然后继续增大到最大值，Hy-α8与Hy-α10两种旋流器切向速度变化呈线性增加趋势也逐渐增大到最大切向速度，随着锥角的增加，旋流器内部所能达到的最大切向速度点值逐渐减小，Hy-α5旋流器的最大切向速度值最高。因此，其他设置参数一致情况下，旋流器锥角增加对内外涡流的分界面影响很小，但会改变其旋转强度，Hy-α5结构旋流器内部流场的旋转强度最大。

4 压力降影响分析

水力旋流器的压力降为进口处压力与溢流出口管(或底流出口)处的压力之差。图5为不同锥角结构旋流器内部压力降的分布对比图，对比截面为旋流器的纵向截面z=0，由图可见在截面z=0上，旋流器内部压力降由旋流器器壁处向中心逐渐增大，在旋流器中心处达到最大值，沿旋流器器壁向底流出口方向压力降呈逐渐增大趋势，在旋流腔内部，旋流器中心与溢流出口底部相交位置处出现最大压力降值，且由该位置沿旋流器中心轴向向上到溢流出口和向下到底流出口截面，压力降呈现出逐渐降低趋势，即3种不同锥角旋流器内部的最大压力降均发生在溢流出口伸入部分底部。3种不同锥角旋流器所达到的最大压力降不同，锥角越小压力降越大，因Hy-α5旋流器锥段最长，底流压力降与溢流出口相比其他锥角结构旋流器压力降则更高；Hy-α8和Hy-α10旋流器，由于锥段减小，底流出口压力降明显低于溢流出口压力降。因此当旋流器其他设置参数不变时，仅锥角变化时对旋流器内部压力降的影响较为明显。

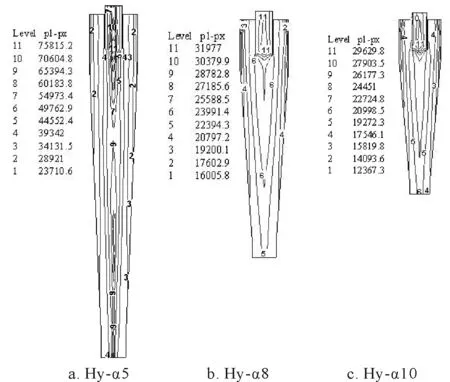
图5 不同锥角旋流器内部z=0截面上的压力降分布对比

由图5可见旋流器内部主要压力降分布包括溢流出口压力降Δpo，底流出口压力降Δpu和溢流伸入管处最大压力降Δpmax，对比不同锥角结构旋流器的主要压力降分布如图6所示。由图可见，随锥角增加压力降呈逐渐降低趋势，锥角越小压力降越大，且溢流压力降比底流压力降增加幅度也最大，锥角由8°变化到10°时二者压力降变化较小；底流压力降最低，因为最高压力降分布在溢流管伸入部分底部，与溢流出口较近，溢流压力降比最高压力降值降低幅度不大。

5 砂相体积分数分布影响分析

砂相经旋流器离心分离后，主要分布在旋流器器壁临近区域，因此主要对比不同锥角结构旋流器器壁临近区域内的砂相体积分数Fs分布。在相同操作参数下，不同锥角旋流器固相体积分数梯度分布如图7所示，对比可见，砂相经旋流腔和锥段分离后基本沿旋流器内壁流向底流出口，整体上底流含砂浓度最高。Hy-α5、Hy-α8和Hy-α10旋流器所达到的底流砂相体积分数最高值分别为29.9%、20.0%和17.5%。

图7 不同锥角旋流器砂相体积分数梯度分布

为进一步对比底流出口含砂浓度受锥角结构变化的影响，针对底流出口截面上的砂相体积分数分布曲线进行对比，如图8所示。由图可见，底流出口截面不同径向位置处的砂相体积分数是变化的，基本呈轴向对称分布，且由边壁到底流出口中心处随半径减小而逐渐降低，在临近边壁7mm范围内，也是旋流器底流出口砂相含量最集中的部分，含砂体积分数随锥角的增加而逐渐降低，Hy-α5结构旋流器的底流出口含砂体积分数分布最高；在中心处和临近部分，含砂相体积分数很小，小于0.1%，其分布对旋流器底流出口含砂浓度影响较小。整体上Hy-α5结构旋流器的底流出口含砂浓度最高。

图8 不同锥角旋流器底流出口截面上砂相体积分数分布曲线对比

6 固液分离效果影响分析

除砂分离效率Es为底流出口固相砂的质量流率与入口来液中固相砂质量流率的比：

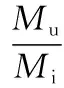
(1)

式中Mi——入口砂的质量流率，kg/s；

Mu——底流出口砂的质量流率，kg/s。

计算得出不同锥角结构旋流器除砂分离效率变化如图9所示。由图可见，旋流器锥角变化对油田采出液砂相分离效率影响较大，在研究范围内，锥角越小旋流器除砂分离效率越高，当锥角为5°时，旋流器除砂分离效率最高可达96.30%。

7 结论

7.1不同锥角结构旋流器的切向速度变化趋势基本一致，截面I上切向速度呈周向对称分布，以最大切向速度为界，旋流器内部速度场被分为内涡流区和外涡流区现象明显，随着锥角的增加，旋流器内部所能达到的最大切向速度点值逐渐减小，旋流器锥角变化对速度场内外涡流的分界面径向位置影响较小，但对其旋转强度影响较大，锥角为5°旋流器内部流场的旋转强度最大。

7.2旋流器内溢流管伸入管底部所产生的压力降值最大，溢流出口压力降次之，底流出口的压力降最低，锥角越小压力降越大。

7.35°锥角结构旋流器的底流出口含砂体积分数最大，且砂相主要分布在旋流器器壁临近区域，该结构计算得出的砂相分离效率也最高。

7.4综上可见，在一定范围内减小旋流器锥角可以提高除砂效率，但其压力降也会增大，实际当中应综合考量除砂分离效率与生产能耗等进行参数选择。

[1] 吕瑞典，李君裕，王远明，等.油井产液除砂旋流器试验研究[J].石油机械，1995，23(6)：18～23.

[2] 张丹，陈晔.锥角对固-液水力旋流器流场及其分离性能的影响[J].流体机械，2009，37(8)：11～16.

[3] 高淑玲，魏德洲，韩聪，等.底流口直径和锥角对旋流器流场的影响[J].东北大学学报(自然科学版)，2010，31(5)：728～732.

[4] 卢涛.矿物颗粒在旋流复合力场中运动行为的数值模拟[D].沈阳：东北大学，2011.

[5] 蒋明虎，刘道友，赵立新，等.锥角对水力旋流器压力场和速度场的影响[J].化工机械，2011，38(5)：572～576.

[6] 赵立新，李枫.离心分离技术[M].哈尔滨：东北林业大学出版社，2006.

[7] Zhao L X，Jiang M H，Xu B R，et al.Development of a New Type High-efficient Inner-cone Hydrocyclone[J].Chemical Engineering Research and Design，2012，90(12)：2129～2134.

[8] 赵立新，韩丽艳，郑国兴，等.同向出流倒锥式旋流器的结构模拟分析[J].流体机械，2013，41(2)：19～24.

[9] 徐保蕊.T形管油水分离器流场分布特性及分离性能研究[D].大庆：东北石油大学，2012.

[10] 赵立新，王尊策，李枫，等.液液水力旋流器流场特性与分离特性研究(一)——锥角变化对切向速度场的影响[J].化工装备技术，1999，20(4)：1～3.

[11] 赵立新，李枫，王尊策，等.液液水力旋流器流场特性与分离特性研究(二)——锥角变化对轴向速度场的影响[J].化工装备技术，1999，20(5)：1～3.

[12] 赵立新，王尊策，蒋明虎.液液水力旋流器流场特性与分离特性研究(三)——水力旋流器径向速度测试方法[J].化工装备技术，1999，20(5)：4～6.

NumericalSimulationofConeAngleEffectonDe-sandingPerformanceofHydrocyclone

ZHANG Xiao-guang1, ZHAO Li-xin1,XU Bao-rui1, JIANG Ming-hu1, DENG Xin2

(1.CollegeofMechanicalScienceandEngineering,NortheastPetroleumUniversity,Daqing163318,China;2.ChinaPetroleumPipelineEngineeringCorporation,Langfang065000,China)

The necessities of de-sanding produced liquid in oilfields were introduced, including both structure and fundamental principle of the cyclone-desander. Through making use of Fluent software and taking the produced fluid from an oilfield as a separation object, the research on numerically-simulating variable cone angles’ structure of the 56mm-diameter-cyclone-desander was implemented to obtain the distribution and the variation law of the velocity, pressure drop and sand phase volume fraction. Comparing the sand separation efficiency of the hydrocyclone with different cone angles shows that, the tangential velocity (vt) in the cyclone is maximum when the cone angle is 5° and the sand volume fraction distribution in the bottom outlet is the highest along with a larger pressure drop and a sand separation efficiency up to 96.30%.

hydrocyclone, cone angle, desanding, separation performance, numerical simulation

*国家“863”计划课题(2012AA061303)，国家教育部高等学校博士学科点专项科研基金课题(20132322110002)。

**张晓光，女，1984年1月生，讲师。黑龙江省大庆市，163318。

TQ051.8

A

0254-6094(2016)06-0798-05

2015-12-25，

2016-10-28)