一道解析几何试题的命制与结论推广

●王志良 (安溪第一中学 福建泉州 362400) ●杨苍洲 (泉州第五中学 福建泉州 362000)



一道解析几何试题的命制与结论推广

●王志良 (安溪第一中学 福建泉州 362400) ●杨苍洲 (泉州第五中学 福建泉州 362000)

坐标法是解析几何的基本思想方法，坐标系是解决平面几何问题中化“形”为“数”的重要工具，高中数学试题的命制应注重对知识本质思想的考查.圆锥曲线有着很多优美的性质，它们往往可以作为解析几何试题命制的素材.

解析几何;圆锥曲线;试题命制;结论推广

笔者有幸参与了2015年福建省泉州市的质检命题工作，在一道解析几何试题的命制过程中，感触颇深，同时也“意外”地发现了一些有关圆锥曲线的一般性结论.下面谈谈该试题的命制与结论的推广，与同行交流探讨.

1 试题命制

1.1 命制构想

根据命题组的分工安排，命制一道解析几何解答题是笔者的任务之一.于是，笔者设想从解析几何的基本思想——坐标法出发，让考生合理地选择坐标系，考查运算求解能力；以抛物线为考查内容，通过相切问题与导数进行交汇，进而使试题内容丰富饱满.

1.2 试题内容

题目 已知点O,F分别是抛物线Γ的顶点和焦点，且|OF|=1，点P在射线OF上.过点P作直线l交抛物线Γ于点A,B，分别过点A,B作抛物线的切线l1,l2,设2条切线的交点为Q.

1)试选择一个图形(如图1和图2所示)，求抛物线Γ在适当的平面直角坐标系下的标准方程.

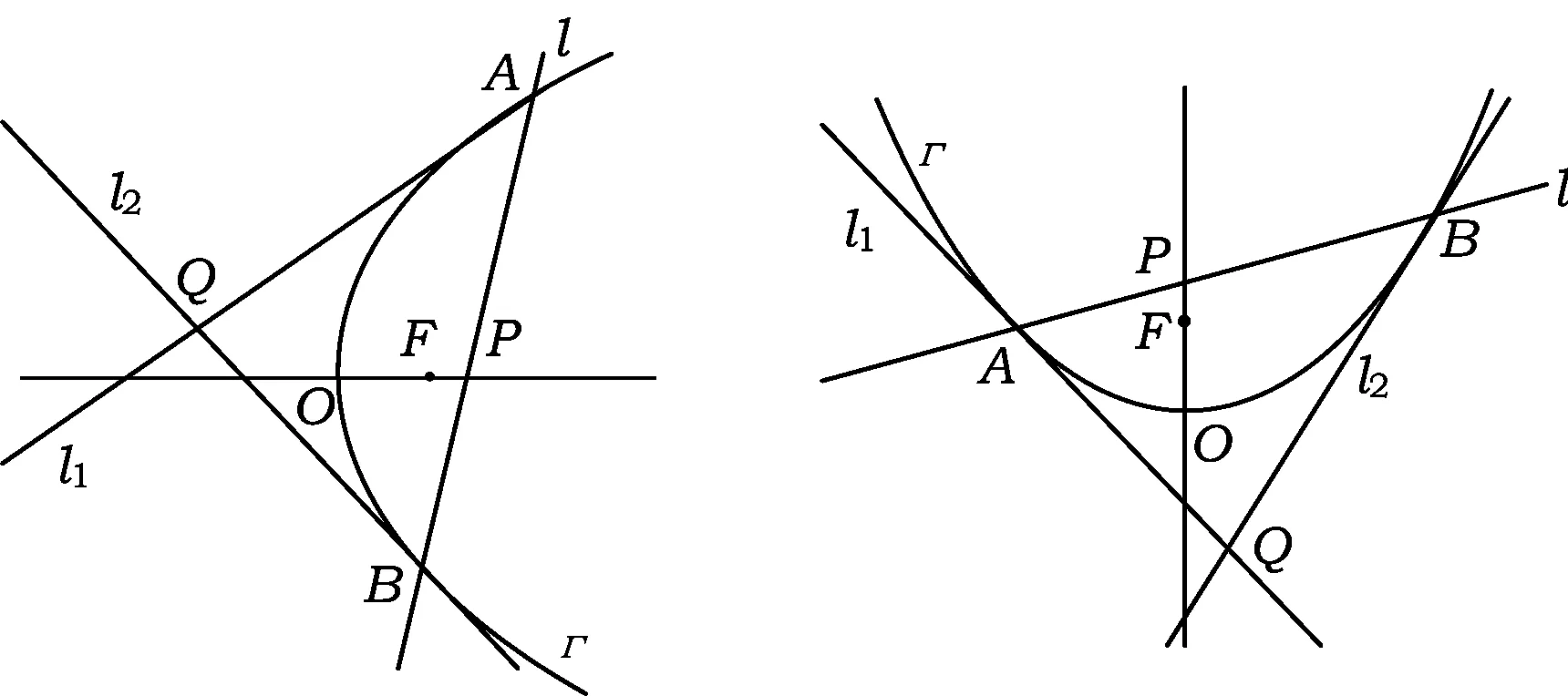
图1 图2

2)在第1)小题的条件下，①证明：当|OP|的长度不变时，直线l1,l2的斜率之积为定值；②若l1⊥l2，请直接确定点P的位置.

(2015年福建省泉州市第二次数学模拟考试

第19题)

图3

1)解 选择图2，以O为原点、OF所在直线为y轴建立平面直角坐标系xOy(如图3所示)，则F(0,1)， 故抛物线Γ的标准方程为x2=4y.

x2-4kx-4m=0，

可得x1x2=-4m，从而

②若l1⊥l2，则

k1k2=-m=-1，

故点P的坐标为(0,1)，即点P与点F重合.

1.3 试题评析

本题主要考查直线的方程、抛物线的定义、直线与抛物线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等[1]．本题有以下几个亮点：

1)重视数学本质思想.坐标法是解析几何的基本思想方法，是利用代数手段研究平面图形的重要方法[2].本题通过让学生自主建系，得到抛物线的标准方程，既考查了坐标法，又考查了抛物线的标准方程在坐标系中的位置特征.

2)突出考查高考数学的能力要求.通过合理地选择坐标系，即合理地选择运算途径，以达到简化计算的目的，从而实现运算求解能力的“自然”考查.

3)倡导开放探索，关注创新意识[3].《考试说明》中指出：高考中可适当设置开放性、探索性试题，考查创新意识和创新精神[1].在本题中，先是探究证明当|OP|长度不变时，直线l1,l2的斜率之积为定值；然后再根据所得结论进行推测该定值与|OP|的长度关系，即确定点P的位置，使试题具有深厚的探究气息和较高的考查价值.

2 结论推广[4]

在本题的探究中，笔者借助软件GeoGebra让点P在抛物线(标准方程形式下)的对称轴上移动，探究其一般性结论，发现：

命题1 若过点P(0,m)的直线与抛物线Γ:x2=ay(其中a≠0)交于点A,B，分别过点A,B作抛物线的切线l1,l2，且l1,l2的斜率分别为k1,k2，则k1k2=-m.

在探究过程中，笔者又想到探究相关的轨迹问题，进而借助软件并结合证明，很快地发现了命题3.

图4

命题3 如图4，已知抛物线Γ:x2=2py(其中p>0).若点P(x0,y0)为坐标平面内的一定点，过点P的动直线l与抛物线Γ交于点A,B，过A,B作抛物线Γ的切线l1,l2，2条切线交于点Q，则点Q的轨迹为直线x0x=p(y+y0)(除抛物线开口内的部分).

命题4 已知抛物线Γ:y2=2px(其中p>0).若点P(x0,y0)为坐标平面内的一定点，过点P的动直线l与抛物线Γ交于点A,B，过点A,B作抛物线Γ的切线l1,l2，2条切线交于点Q，则点Q的轨迹为直线y0y=p(x+x0)(除抛物线开口内的部分).

特别地，当点P在抛物线的对称轴上时，可得命题5和命题6.

命题5 已知抛物线Γ:x2=ay(其中a≠0).若过点P(0,m)的动直线l与抛物线Γ交于点A,B，过A,B作抛物线Γ的切线l1,l2，2条切线交于点Q，则点Q的轨迹为直线y=-m(除抛物线开口内的部分).

命题6 已知抛物线Γ:y2=ax(其中a≠0).若过点P(m,0)的动直线l与抛物线Γ交于点A,B，过A,B作抛物线Γ的切线l1,l2，2条切线交于点Q，则点Q的轨迹为直线x=-m(除抛物线开口内的部分).

由于圆锥曲线在很多方面具有统一性，笔者进一步探究圆、椭圆、双曲线，经过验证，发现下列命题：

命题7 如图5，已知⊙O:x2+y2=r2(其中r>0).若点P(x0,y0)为坐标平面内的一定点(异于圆心O)，过点P的动直线l与⊙O交于点A,B，过点A,B作⊙O的切线l1,l2，2条切线交于点Q，则点Q的轨迹为直线x0x+y0y=r2(除圆内部分).

图5 图6

特别地，当点P为椭圆的焦点时，可得命题9.

图7

特别地，当点P为双曲线的焦点时，可得命题11.

[1] 福建省考试院．2015年普通高等学校招生全国统一考试福建省语文·数学·英语考试说明[M]．福州：福建教育出版社，2014.

[2] 中华人民共和国教育部．普通高中数学课程标准[M]．北京：人民教育出版社，2003.

[4] 杨苍洲，王志良.一道解析几何高考试题的题源探究与推广[J].中学教研(数学)，2014(6)：1-6.

2016-03-17；

2016-04-20.

王志良(1977-)，男，福建泉州人，中学一级教师，研究方向：数学教育.

O123.1

A

1003-6407(2016)06-36-03