巧用建系 以数解形

●虞 会 (蛟川书院 浙江宁波 315201)



巧用建系 以数解形

●虞 会 (蛟川书院 浙江宁波 315201)

在初中阶段，平面直角坐标系是数与形的又一次完美结合.把一个几何图形放到平面直角坐标系中，图形中的点就有了坐标，图形中的线就有了解析式.当几何题难以用几何的方法来解决的时候，不妨放到平面直角坐标系中去，用代数的方法去解决.

直角坐标系;几何代数；运动轨迹

在初中阶段，平面直角坐标系是数与形的又一次完美结合.当我们把一个几何图形放到平面直角坐标系中，图形中的点就有了坐标，图形中的线就有了解析式.当几何题难以用几何的方法来解决的时候，不妨放到平面直角坐标系中去，用代数的方法去解决，往往有“山穷水尽疑无路，柳暗花明又一村”的感觉.

图1

例1 如图1，正方形ABCD和正方形CGEF的边长分别是2和3，且点B，C，G在同一直线上，M是线段AE的中点，联结MF，求MF的长.

(2013年浙江省宁波市初中自主招生试题)

本题的几何方法很多，利用条件中“M是线段AE的中点”这个条件，可以倍长中线(如图2和图3)，也可以构造中位线(如图4和图5).而这些辅助线在平常的学习中不经常遇到，难度也较大，学生不容易想到.

图2 图3

图4 图5

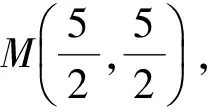
图6 图7

例2 如图7，已知正方形ABCD的面积为36，E,F分别为边AB,BC上的点，AF和CE相交于点G，并且△ABF的面积为9，△BCE的面积为12，则四边形BEGF的面积为______.

分析 根据已知条件可知BE=4，BF=3，联结BG，则

S四边形BEGF=S△EBG+S△BGF=

只要求出GM，GN的长即可，联想到求点G坐标，而点G恰好是直线AF,CE的交点.

解 以B为原点、AB为x轴建立如图7所示的平面直角坐标系.由题意可知B(0,0)，A(-6,0)，F(0,3)，C(0,6)，E(-4,0)，从而

故

于是

例3 如图8所示，在△ABC中，∠ACB=90°，BC=2AC，以BC为底作等腰直角△BCD，E是CD的中点，求证：AE⊥EB.

分析 要证AE⊥EB，联想到直线AE,BE的斜率k相乘等于-1，本题的难点是如何建立恰当的平面直角坐标系.建立平面直角坐标系的几个原则：1)利用题目中的直角;2)利用单位“1”;3)点坐标表示简便.

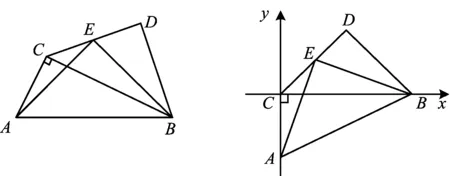
图8 图9

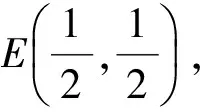
又因为

kAE·kBE=-1，

所以

AE⊥EB.

例4 已知线段AB=10，AC=BD=2，点P是线段CD上的一个动点，分别以AP,BP为边向上、向下作正方形APEF和PHQB.设正方形对角线的交点分别为O1,O2，求点P从点C运动到点D时线段O1O2的中点G的运动路径长为______.

(2013年广西壮族自治区桂林市数学中考试题)

分析 此题得分率很低，难点在于对点G运动路径的判断.如果用几何的方法来解决，思维跨度较大，难以想到,不妨放到平面直角坐标系中去，用代数法来证明点G运动的路径是一条线段，即只要说明点G的横纵坐标满足一次函数解析式.

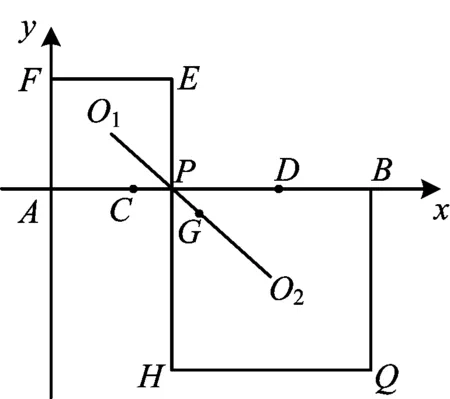
图10

小结 对于运动型几何问题，在借助平面直角坐标系解决时，常常会出现含参的解析式，这对学生的计算能力和理解能力有较高的要求.

例5 如图11，在矩形ABCD中，AB=5,BC=4,点E为边AB上的一个定点，且AE=2，点P为直线CD上的一个动点,在PE的右侧作PQ⊥PE,PQ=PE．在点P沿直线CD运动的过程中,求DQ+EQ的最小值.

(2014年浙江省宁波市初中自主招生试题)

分析 点D和点E是定点，点Q是动点，要求DQ+EQ的最小值，需要知道点Q的运动轨迹，可以借助平面直角坐标系来解决，得出点Q的运动路径是一条直线后，此题就转化为将军饮马模型.

图11 图12

解 以A为原点、AB为x轴建立如图12所示的平面直角坐标系，过点P作PF⊥AB于点F，过点Q作QG⊥CD于点G.令DP=a，由题意可知A(0,0)，E(2，0)，D(0,4).由PQ⊥PE,且PQ=PE,知

△PEF≌△PQC，

从而

PG=PF=4，QG=FE=2-a，

于是

Q(4+a,6-a)，

多一种方法，多一种选择.初中阶段学习过的平面图形主要有三角形、四边形、圆，而三角形、四边形的边可以用直线解析式来描述，圆也可以用圆的解析式来描述，在初中竞赛和提前招生考试中常常会遇到.因此对于程度较好的学生来说,比较容易接受该方法.初中建立平面直角坐标系法在高中即是解析几何法，虽在教材中并不要求，但是在新课标所提倡的模型思想中，可以提高学生学习数学的兴趣和应用意识，也可以体现出新课程基本理念中不同的人在数学上得到不同的发展.

2016-03-11；

2016-04-26.

虞 会(1984-)，男，浙江宁波人，中学一级教师，研究方向：数学教育.

O123.1

A

1003-6407(2016)06-26-02