最值互嵌问题的解题策略
2016-12-26王红权杭州市基础教育研究室浙江杭州310006
●王红权 (杭州市基础教育研究室 浙江杭州 310006)
最值互嵌问题的解题策略
●王红权 (杭州市基础教育研究室 浙江杭州 310006)
解答最值互嵌问题对学生来说比较困难.理清这类问题的解题规律和操作策略可以有效地帮助学生提高解题水平.解答这类问题常常需要构造图像、对称式、不等式等.文章结合实例,分析构造的具体策略.
最值互嵌;解题策略;构造
最值互嵌问题历来是数学竞赛命题的一个热点,也是教学中的一个难点.最近几年这类问题正悄悄地由竞赛转向高考.命题专家给出的解答往往很突然,变化无穷且一题一法,不易为广大学生想到.学生解答这类问题普遍感觉比较困难,很难获得普遍有效的方法,更何况理解这些抽象的记号本身也需要下点功夫.笔者认为有必要对这类问题作系统的梳理,本文试图通过几个例题给出这类问题的一般解题策略,供大家参考.
本文约定min{a1,a2,…,an}表示数a1,a2,…,an中的最小者,max{a1,a2,…,an}表示数a1,a2,…,an中的最大者.max min{a1,a2,…,an}表示“求最小值中的最大值”,min max{a1,a2,…,an}表示“求最大值中的最小值”.
1 求最小值中的最大值
策略1 对于单变量问题,画图是非常有效的方法,不仅直观而且易于上手.初学者从这里开始接触这些记号,比较容易理解记号所要表示的含义和最值互嵌本身的内含,不至于一开始就把初学者挡在门外了.
1.1 图像法
通过画出函数图像,并根据图像的位置直接看出答案.这种方法一般适用于单变量问题.

( )
A.-1 B.1 C.2 D.3
(2014年浙江省高中数学竞赛试题)

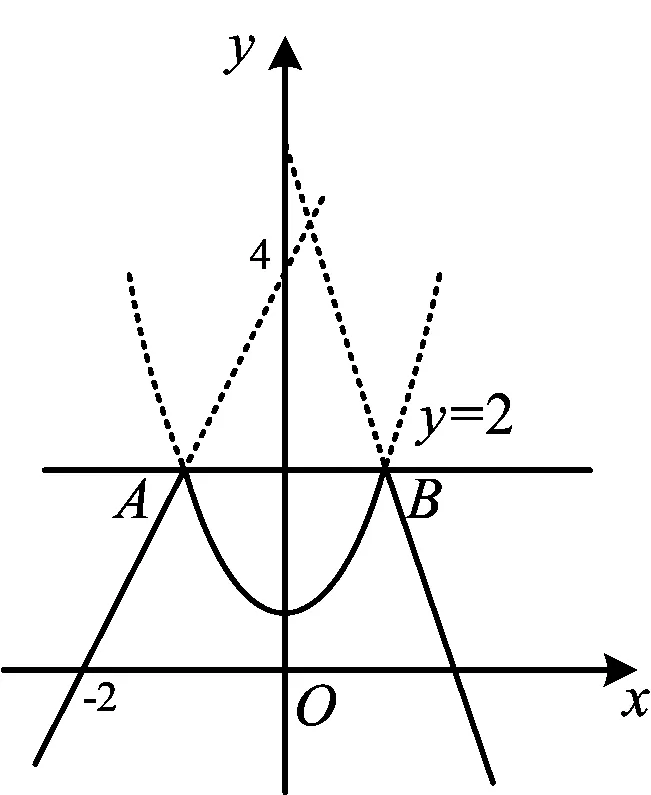
图1
评注 如果问题只含有1个变量,一般只需画出函数图像,观察图像位置关系便可获得答案.
策略2 对于多变量问题,常常先设A=min{a1,a2,…,an},则A≤a1,A≤a2,…,A≤an,然后通过构造法来解决.
1.2 构造对称式法
在多变量问题中,已知各式往往是不对称的,难以利用重要不等式求解.通过构造对称式,即可利用重要不等式求出A的最大值.

解 由题意知
把这2个不等式相乘,并利用不等式x2+y2≥2xy,得
即
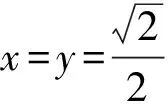
1.3 不等传递法
挖掘a1,a2,…,an内在逻辑不等关系,通过不等式自身具有的传递特点,构造含有A的不等式,解该不等式即可获得A的最大值.
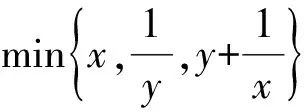
(2003年北京市高中数学竞赛试题)

可得
从而
于是
A2≤2,
即



(2006年浙江省高中数学竞赛试题)
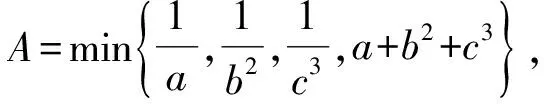
0 可得 从而 于是 A2≤3, 即 1.4 不等式构造法 通过挖掘a1,a2,…,an内在等量关系,构造含有A的不等式,通过解不等式即可获得A的最大值. 例5 设x>1,y>1,A=min{logx2,log2y,logy8x2},则A的最大值为______. (2006年陕西省高中数学竞赛试题) 解 由题意知 0 因为 logx2· (log2y·logy8x2-3)= 又 A(A2-3)≤logx2·(log2y·logy8x2-3), 得 A(A2-3)≤2, 即 A3-3A-2≤0, 分解因式得 (A-2)(A+1)2≤0, 评注 本题的关键在于发现等量关系 logx2·(log2y·logy8x2-3)=2, 从而构造关于A的三次不等式A3-3A-2≤0,通过解不等式得到A的最大值. 2.1 图像法 如前面所述,该方法对解决一元问题适用. 例6 对a,b∈R,记 函数f(x)=max{|x+1|,|x-2|}(其中x∈R)的最小值是______. (2006年浙江省数学高考理科试题第12题) 图2 策略3 对于多变量问题,常常先设A=max{a1,a2,…,an},则A≥a1,A≥a2,…,A≥an.这类问题相对于前面的问题,解决的方法要简单些,常用的方法有构造对称式和分类讨论. 2.2 构造对称式法 这种方法与前面求“最小值的最大值”类似,但不同的是这里的构造对称往往是为了利用条件,因此构造的方向就是如何用好条件. 例7 设a,b,c∈R,且a+b+c=1,求min max{a+b,b+c,a+c}. 解 设A=max{a+b,b+c,a+c},则 A≥a+b,A≥b+c,A≥a+c, 从而 3A≥ (a+b)+(b+c)+(a+c)= 2(a+b+c)=2, 得 评注 如何从a+b,b+c,a+c构造利用好条件a+b+c=1是本题的关键. 2.3 放缩法 对于一类带有绝对值的问题,可以通过三角形不等式:|a|-|b|≤|a+b|≤|a|+|b|(或|a|-|b|≤|a-b|≤|a|+|b|)放缩得到. (2006年河北省高中数学竞赛试题) 解 根据题意得 A≥|f(0)|=|q|, 2A≥2|f(1)|=|2p+2q+2|, A≥|f(2)|=|2p+q+4|, 上述3个式子相加得 4A≥ |q|+|2p+2q+2|+|2p+q+4|≥ |q-2p-2q-2+2p+q+4|=2, 故 例9 设a,b∈R,不等式max{|a+b|,|a-b|,|2 006-b|}≥c恒成立,则常数c的最大值是______. (2006年上海市高中数学竞赛试题) 解 设A=max{|a+b|,|a-b|,|2 006-b|},则 A≥|a+b|,A≥|a-b|,A≥|2 006-b|, 故 4A≥ |a+b|+|a-b|+2|2 006-b|≥ |(a+b)+(b-a)+2(2 006-b)|= 4 012, 得A≥1 003,当a=0,b=1 003时等号成立,因此c的最大值为1 003. 评注 例8和例9构造了含“4A”的不等式是为了能利用三角形不等式放缩后凑得一个常数.这里的系数可以用待定系数法得到. 2.4 分类讨论法 分类讨论的最大优点在于各个击破,通过分类讨论使得一些本来困难的求解过程变得容易.在求解“最大值的最小值”问题中,最麻烦的事是如何剔除那些“鱼目混珠”的量,分类讨论是其中一种有效的方法. 例10[1]设x,y∈R,A=max{|x+y|,|x-y|,|1-x|,|1-y|},试求A的最小值. 解 1)若xy≥0,因为 |x-y|≤|x|+|y|=|x+y|, 所以 max{|x+y|,|x-y|,|1-x|,|1-y|}= max{|x+y|,|1-x|,|1-y|}. 由题意得 A≥|x+y|,A≥|1-x|,A≥|1-y|, 故 3A≥ |x+y|+|1-x|+|1-y|≥ |(x+y)+(1-x)+(1-y)|=2, 2)若xy<0,max{|1-x|,|1-y|}>1,则 A= max{|x+y|,|x-y|,|1-x|,|1-y|}> 评注 本题通过分类讨论,发现当xy<0时结论显然成立;当xy≥0时,通过分析剔除无关量“|x-y|”,这是解决这个问题的关键. (2013年江苏省常州市高三数学调研试题) 解 由题意知 于是 故 即A≥2. ②当0 从而 于是 故 即A≥2. 综上所述,A的最小值为2. 求解最值互嵌问题的策略是多元的.如何选择合理的解题策略,需要有敏锐的观察能力,更需要心中有“法”.因此归纳一类问题的解题策略对学生入门和初步掌握解决该类问题是有帮助的.教学中教师需要引导学生“发现一类问题,归纳一类问题,提出一些策略”,解决学生入门难的问题,帮助学生减轻学习的负担. [1] 孔祥新.求双层复合最值的解题策略[J].中等数学,2006(11):11-13. [2] 郑日锋.不等式[M].杭州:西冷印社出版社,2006. [3] 席华昌.一个最大数命题的多种证法[J].中学数学杂志,2005(3):36-37. 2016-03-27; 2016-04-15. 王红权(1970-),男,浙江杭州人,中学高级教师,研究方向:数学教育. O122.1 A 1003-6407(2016)06-12-04

2 求最大值中的最小值



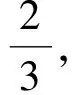



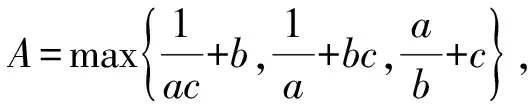
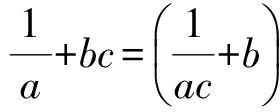
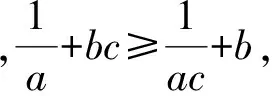
3 结束语
