Clos交换结构的基于相异代表组的路由控制算法
2016-12-24刘晓锋
刘晓锋
(西华师范大学 计算机学院,四川 南充 637009)
Clos交换结构的基于相异代表组的路由控制算法
刘晓锋
(西华师范大学 计算机学院,四川 南充 637009)
Clos交换结构作为多级结构的典型代表在以大数据、数据中心网络为特征的云计算时代再次受到业界的关注,但目前应用于Clos交换结构的分组控制算法(或调度算法)却较难以适应大数据及数据中心网络的低延迟,低能耗等的性能需求。因此,根据Clos交换结构中分组调度的本质,利用相异代表组(SDR)基本思想为每个分组分配不同中间级交换模块,从而实现无阻塞交换,同时以示例和理论上证明了该算法的可行性及算法实现。由于该控制算法有效避免了大量的仲裁信息,因此能有效降低交换延迟,提高交换吞吐率。
分组交换;相异代表组;Clos网络;控制算法
0 引 言
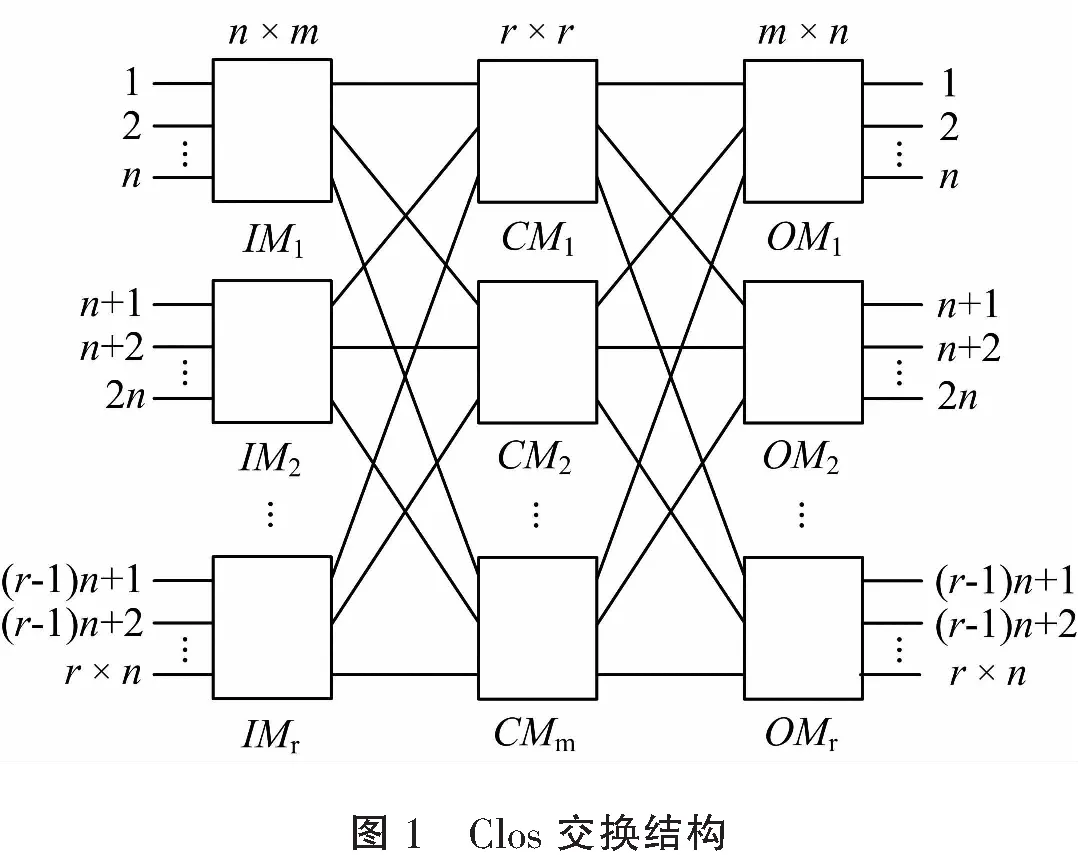
Clos网络[1]作为电话交换网络的产物,却在分组交换中扮演了非常重要角色,特别是在以大数据、数据中心网络为特征的云计算成为主流运维模式的背景下,它作为数据中心网络的物理架构再次成为企业及学术界的研究焦点。一个Clos交换网络是由输入级、输出级和中间级连接而成的3级结构,级与级之间由通信链路通过部分互连的方式连接而成,如图1所示。输入级的交换模块称为输入模块(input module,IM),输出级的交换模块称为输出模块(output module,OM),中间级的交换模块称为中间模块(center module,CM)。每个IM(OM)是一个n×m(m×n)的交换矩阵,每个CM是一个r×r的交换矩阵,而且每个IM(OM)模块都有唯一链路连接一个CM模块,因此一个Clos交换网络的相关属性完全由参数n,m,r来决定。当m≥2n-1,此网络严格无阻塞[1];当m≥n,为可重排无阻塞[2]。
交换网络的一个指派(assignment)是所有输入/输出端口组成有序对<输入端口,输出端口>的集合,而且每个端口只能出现在一个有序对中。有序对<输入端口,输出端口>指明了分组在交换结构中的入口和出口。在交换结构内部如果存在不相交(即不产生冲突)的路由路径来链接指派中的每个有序对,则称此指派是可行的(realizable)。对Clos交换网络来说,一个指派是否可行与CM的分配策略紧密相关。如果CM分配不合理,则其内部的路由路径可能会产生冲突,最终致使分组丢失,交换吞吐率降低。为了确保一个指派是可行的,通常需要相应的路由控制算法来控制每个有序对<输入端口,输出端口>的路由路径。在设计交换网络内部的路由控制算法时,可将路由问题转化矩阵分解(matrix decomposition)问题,二分图匹配(bipartite matching)问题及边着色(edge coloring)等问题[3]。本文根据CM的分配原则及分配目标,以相异代表组(system distinct representative, SDR)为基础设计一款路由指派算法能有效避免大量的仲裁信息。
1 分组控制算法相关研究
交换结构的控制算法(或调度算法)主要完成在所有输入-输出间选择一条没有冲突的交换路径,从而实现快速高效的分组交换,达到合理利用网络资源,提高吞吐率和降低延迟,因此控制算法的性能直接影响交换结构的交换性能。
在交换结构的输入-输出间寻找无冲突匹配的数学模型就是二分图的匹配问题。为了提高吞吐率,调度算法需要在二分图的匹配中找到一个最大匹配(maximum size matching)。目前实现最大匹配的算法虽能达到100%的吞吐率,但其实现复杂度比较高(O(N2.5))[4],而且可能导致不稳定性及饿死现象[5],在实际应用中很少采用。通常采用一些近似手法通过多次迭代来逼近一个最大匹配,较为知名的控制算法如CRRD/CMSD[6],PIM[7],iSLIP[8]。虽然这些调度算法所针对的交换结构有一定的差异,但其采用的基本思想是一致的,均为请求-授权-接受(request-grant-accept,RGA)模式在输入-输出间建立匹配。基于RGA匹配模式的控制算法会在输入端与输出端之间产生大量的仲裁信息,这不仅会增加交换延迟,而且还会增加信息存储的负担,在高速环境中控制也比较复杂。
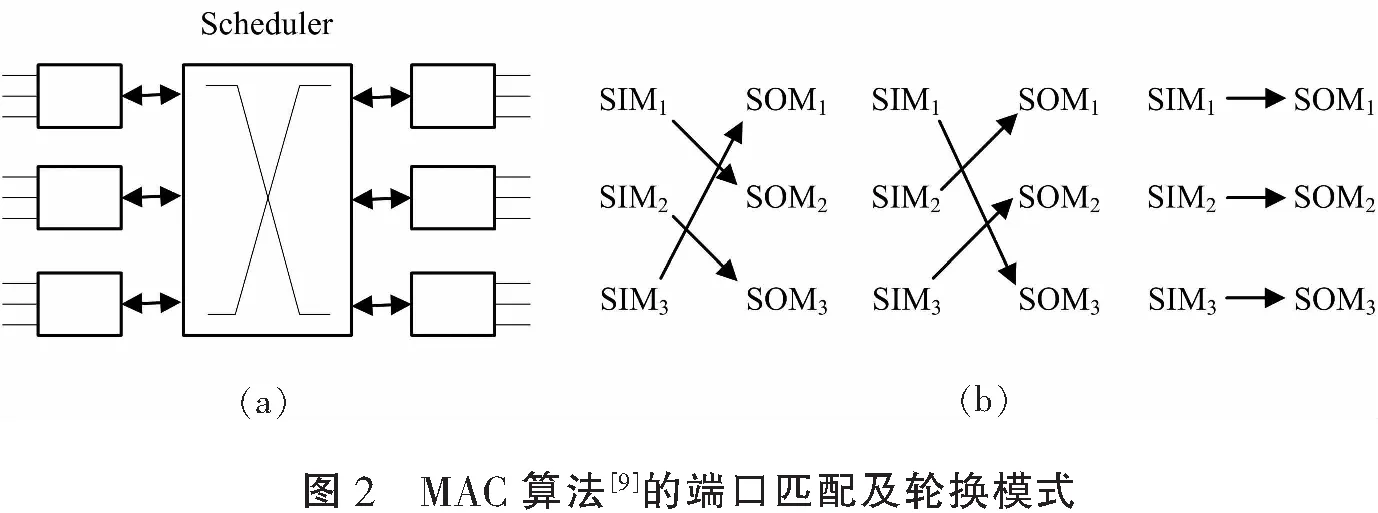
MAC[9]和Distro[10]是两款以多级体系结构为硬件平台的调度算法。Distro算法利用静态轮转的模式在多级间通过问-答方式来建立输入-输出端口间的匹配。此算法类似于CRRD/CMSD,不同的是Distro采用静态轮转,少了一次“接受”信息的传送,其负面影响就是不能很好适用于任意的流量模式,同样需要逐级传送咨询信息。MAC算法部署了一个类似于单级结构的调度器(如图2(a)所示),去掉了逐级探测的匹配方式,但需要通过两级匹配来完成输入-输出端口的匹配。首先是SIM与SOM的匹配(称为1级匹配),然后在已配对的SIM-SOM所包含的输入与输出端口间进行匹配(称为2级匹配)。1级匹配采用了预先确定的轮换方式(如图2(b)所示);2级匹配就在已配对SIM-SOM所含的输入-输出端口间按RGA模式进行匹配。这样就不需要在多级间传递仲裁信息。
本文提出的基于SDR思想的控制算法去掉基于RGA的询问-应答模式,在匹配成功的输入-输出间直接分配路径,从而提高传输效率,降低传输延迟。
2 基于SDR的控制算法
路由路径指派的终极目标是在分组交换过程中不要产生任何阻塞,为了实现此终极目标,算法对CM的选择必须满足以下2点分配目标:(1)为来自相同IM的分组分配不同的CM;(2)为前往相同OM的分组分配不同的CM。为此先定义如下相关定义及基本定理。
2.1 基本定义
定义1 业务矩阵(traffic matrix)T表示输入交换模块到输出交换模块的请求情况,表示为

元素tij表示源输入模块为IMi,目的输出模块为OMj的分组数,即从IMi→OMj的分组数。
定义2 相异代表组[11]就是为一个集合系的每个集合寻找一个代表元素,而且要求所有的代表元素互不相同。如有集合系S={S1,S2,S3,S4,S5,S6},其中S1={1,2,3},S2={1,2,3,4},S3={2,3,4,5},S4={3,4,6},S5={1,2},S6={1,2,3}。此集合系的相异代表组SDR={3,4,5,6,1,2},即用元素3来代表S1,4代表S2,5代表S3,6代表S4,1代表S5,2代表S6。
定理1[11]假设集合系S由集合M的n个子集合S1,S2,…,Sn构成,即S={S1,S2,…,Sn}。这n个子集合的任意k (k=1,2,…,n)个子集合的并集至少包含M的k个不同元素,则集合系S存在一个相异代表组。
证明 可以对整数k用数学归纳法证明。详细证明过程参见[11]。
下面给出两个关于CM的集合系CM_im(i)和CM_om(j) (1≤i,j≤r)。
定义3CM_im(i)={CM| 源输入模块为IM(i)的分组能使用的CM};CM_om(j) = {CM| 目的输出模块为OM(j)的分组可使用的CM},(1≤i≤r,1≤j≤r)。
这两个集合系中每个集合的初值均为{CM1,CM2,…,CMm}。一个指派中的任意请求有序对〈IMi,OMj〉(1≤i,j≤r)可经过任意CM来实现其交换目的。为了实现上述CM的分配目标,只需在集合CM_im(i)∩CM_om(j)(1≤i,j≤r)中为每个请求有序对分配一个CM,然后在集合CM_im(i)和CM_om(j)中删除此CM,这样可以有效避免各种类型的阻塞。
2.2 基于SDR的控制算法
为了实现CM的分配目标,用一个m位的二进制串来表示定义3中的每个CM集合。串的每一位对应于相应的CM的使用情况。如果某位为1则表示对应的CM可用,否则此CM不可用。如果集合CM_im(i)的初始值为{CM1,CM2,CM3,CM4,CM5},用二进制“11111”表示,在经历了几次分配后此集合变成{CM2,CM5},则二进制为“01001”,因为CM1、CM3和CM4已被分配,对应的二进制串中相应位由1变为0。
为了实现在集合CM_im(i)∩CM_om(j) (1≤i,j≤r)中选择CM,可对相应串进行按位“与”,结果串中数字1所对应的CM可用;然后修改两个串的被选CM对应的位为0。
下面通过一个例子来阐述这种思想。
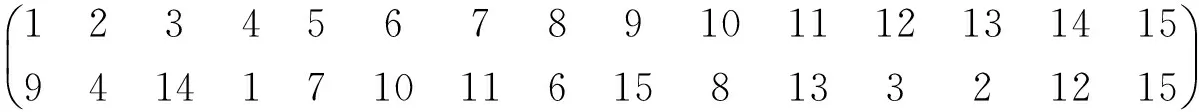
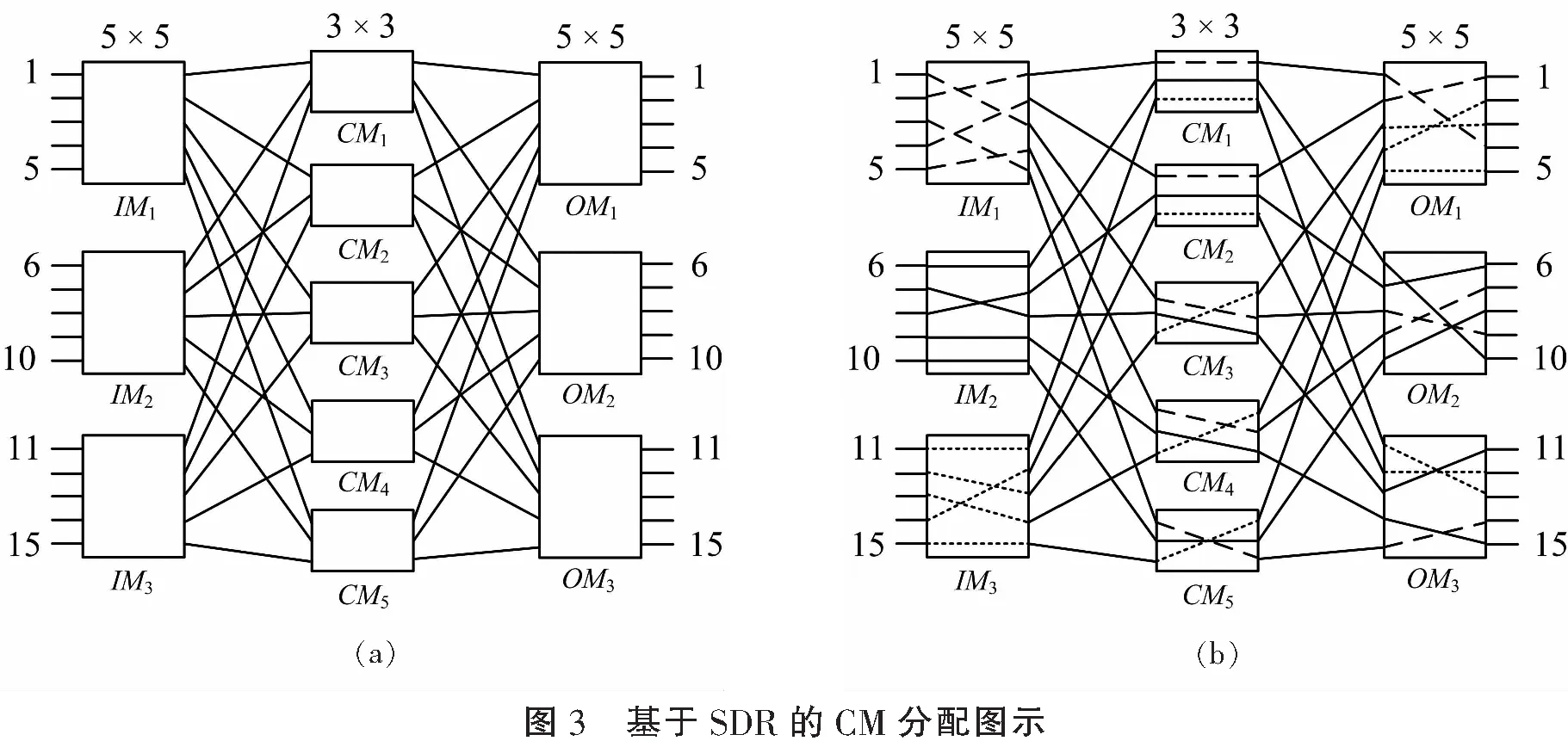
下面讨论中均用二进制串代表集合。
第1步,分析T的第1行元素[2,2,1]。它表示来自IM(1)的5个分组,其中2个到OM(1),2个到OM(2),1个到OM(3)。
①计算CM_im(1)&CM_om(1)=“11111”,这说明5个CM均可用,任意选择2个作为到OM(1)的分组使用,如CM1和CM2。然后修改这两个二进制串中对应位为0,即CM_im(1)=“00111”,CM_om(1)=“00111”。
②计算CM_im(1)&CM_om(2)=“00111”&“11111”=“00111”,这表明只CM3,CM4和CM5可用,如选择CM3和CM4。修改两二进制串为CM_im(1)=“00001”,CM_om(2)=“11001”。
③计算CM_im(1)&CM_om(3)=“00001”&“11111”=“00001”,这表明只有CM5可用,因此只能选择CM5。修改二进制为CM_im(1)=“00000”,CM_om(3)=“11110”。
第2步,分析T的第2行元素[0,3,2]。它表示来自IM(2)的5个分组,其中0个到OM(1),3个到OM(2),2个到OM(3)。
①计算CM_im(2)&CM_om(2)=“11111”&“11001”=“11001”,这表明只CM1,CM2和CM5可用,所以将这3个CM分配给到OM(2)的分组。修改串为CM_im(2)=“00110”,CM_om(2)=“00000”。
②计算CM_im(2)&CM_om(3)=“00110”&“11110”=“00110”,说明当前只有CM3和CM4可用,于是将这两个CM分配给到OM(3)的分组。修改串为CM_im(2)=“00000”,CM_om(3)=“11000”。
第3步,分析T的第3行元素[3,0,2]。它表示来自IM(3)的5个分组,其中3个到OM(1),0个到OM(2),2个到OM(3)。
①计算CM_im(3)&CM_om(1)=“11111”&“00111”=“00111”,结果表明只有CM3,CM4和CM5可用,所以将这3个CM分配给到OM(1)的分组。修改串为CM_im(3)=“11000”,CM_om(1)=“00000”。
②计算CM_im(3)&CM_om(3)=“11000”&“11000”=“11000”,结果表明CM1和CM2可用,于是将这两个CM分配给这两个分组。修改串为CM_im(3)=“00000”,CM_om(3)=“00000”。
所有CM模块按此分配算法不会产生任何阻塞,如图3(b)所示。
3 基于SDR控制算法实现及可行性分析
3.1 算法可行性证明
Clos网络C(n,m,r)在m≥2n-1成立时严格无阻塞,在m≥n成立时可重排无阻塞。本算法的讨论是在m≥n的背景下进行。为讨论的方便,我们进一步假设此网络是对称的,即m=n=r。对于非对称的Clos网络同样可以证明。
如前所述,为请求集IM(i)→OM(o)(o=j1,j2,…,jt)分配CM的过程,为了给来自IM(i)的所有请求分配不同的CM,等价于找集合系CM_om(o)(o=j1,j2,…,jt)的相异代表组。集合系CM_om(o)(o=j1,j2,…,jt)是否存在相异代表组是决定该算法可行性的根本。假设在某个时隙,来自IM(i)(1≤i≤r)的请求有s个。由于来自IM(i)(1≤i≤r)的请求最多有n个,所以s≤n。另外,可能存在多个请求到相同的输出模块,但不存在一个请求到多个不同的输出模块(不考虑多播),因此t,s,n三者存在不等关系:t≤s≤n。下面分两种情况证明集合系CM_om(o)(o=j1,j2,…,jt)存在相异代表组:(1)t=s;(2)t (1)t=s 条件t=s表示来自IM(i)的s个请求到s个不同的输出模块,而集合系CM_om(o)(o=j1,j2,…,jt)中的每个集合都含有m个不同的元素CM1,CM2,…,CMm。因此当t=s≤n≤m关系成立时,集合系的任意k(k≤t)个集合的并集至少含有k个不同元素,根据定理1,此集合系CM_om(o)(o=j1,j2,…,jt)一定存在相异代表组。 (2)t 条件t 假设有来自IM(i)的rh个分组请求到OM(jh) (1≤h≤t),而且满足r1+r2+…+rt=s。现在需要在集合CM_om(jh)中为这rh个分组选出不同元素。为了实现这样的分配目标,现将集合CM_om(jh)映射成一个子集合系(1≤h≤t)。在集合CM_om(jh)中选出rh个不同元素,相当于为子集合系选出一个相异代表组。如例1中,将CM_om(1)映射成两个集合CM_om(l1)和CM_om(l2),在这两个集合中选出相异代表给 经这样映射得到的新集合系共含有s个集合,且每个集合都含有m个不同元素CM1,CM2,…,CMm。根据定理1,当t 综上所述,对可重排非阻塞Clos网络,对任意请求集IM(i)→OM(o)(o=j1,j2,…,jt),集合系CM_om(o)(o=j1,j2,…,jt)一定存在其相异代表组,只要请求集通过这个相异代表组就可完全实现分组的无阻塞交换。 3.2 算法的实现 假设集合系S={S1,S2,…,Sn},且S存在相异代表组。下面基于换元的思想[12]来寻找集合系S的相异代表组。寻找相异代表组的过程如下:从S1中选一个元素a1;从S2从选一个元素a2,但要求a2≠a1,……,从Si中选一个元素ai,确保ai≠aj(j=1,2,…,i-1)。如果这个过程能够进行到最后一个集合Sn,则SDR={a1,a2,…,an}就是集合系S的一个相异代表组,当然一个集合系的相异代表组可能不唯一[11]。如果这个过程进行到某个集合Si,其中的所有元素都已成为其它集合Sj(j=1,2,…,i-1)的代表,导致在Si中找不到不同于aj(j=1,2,…,i-1)的元素作为自己的代表,此时需要调整Sj(j=1,2,…,i-1)的代表,以便在Si中能选出一个不同于aj(j=1,2,…,i-1)的代表。下面给出具体的调整过程。 为了在Si中能选出一个不同于aj(j=1,2,…,i-1)的代表ai,首先构造辅助集合T,然后根据这个集合进行换元,直至找到Si的不同于aj(j=1,2,…,i-1)的代表ai。假设已经得到的相异代表组SDR={a1,a2,…,ai-1},Si={b1,b2,…,bt},且br∈SDR(r=1,2,…,t)。T的初值设为Si,即T=Si={b1,b2,…,bt}。现在逐个考察T的每个元素br(r=1,2,…) (假设T的元素有序的)。如果br是某个集合Sj(j=1,2,…,i-1)的代表,则将Sj中不属于T的元素加入到T中;如果br不是任何集合的代表,而且br∈Sj,则用br作为Sj的新代表换出其原代表aj。如果aj∈Si,则用aj作为Si的代表加入到SDR中,调整过程结束,继续寻找Si+1的代表,否则检查贡献aj的集合Su,用aj作为Su的新代表换出其原代表au,再检查au是否属于Si,如果属于,则让au作为Si的代表,终止调整过程,继续寻找Si+1的代表,否则继续换元直至找到Si的代表为止。下面通过一个例子来说明这个寻找过程。 例2 有一个集合系S1={1,2,3},S2={2,3,4},S3={2,3,4,5},S4={3,5,7},S5={1,2},S6={1,2,3}。首先选出S1,S2,S3和S4的相异代表SDR={1(S1),2(S2),3(S3),5(S4)} (SDR集合中元素a(S)表示a为集合S的代表)。S5的两个元素都已成为其它集合的代表,所以进入调整阶段。整个调整阶段分为辅助集合T的构造及相异代表的替换。首先令T=S5={1,2}。T中元素1是S1的代表,将S1中不属于T的元素3加入T中,得T={1,2,3(S1)} (T集合中元素b(S)表示b来自集合S);因为T中元素2是S2的代表,所以将S2中不属于T的元素4加入T中,得T={1,2,3(S1),4(S2)};T中元素3是S3的代表,将S3中不属于T的元素5加入T中,得T={1,2,3(S1),4(S2),5(S3)};T中元素4当前不是任意集合的代表,终止T集合的构造进入换元阶段。T中元素4来自于S2,就让4作为S2的新代表换出其当前代表2,因为2∈S5,所以2作为S5的代表进入SDR中,得SDR={1(S1),4(S2),3(S3),5(S4),2(S5)}。现在继续找S6的代表。因为S6的所有元素也都成为其它集合的代表,所以也需要调整。令T=S6={1,2,3}。T中元素1是S1的代表,但S1中没有不属于T的元素,不执行任何操作;T中元素2是S5的代表,S5中也没有不属于T的元素;T中元素3是S3的代表,将S3中不属于T的元素4,5加入T中,得T={1,2,3,4(S3),5(S3)};T中元素4是S2的代表,但S2中没有不属于T的元素;T中元素5是S4的代表,将S4中不属于T的元素7加入到T中,得T={1,2,3,4(S3),5(S3),7(S4)};T中元素7当前不是任何集合的代表,但它是来自集合S4,所以让7作为S4的新代表换出其原代表5,但5∉S6,还需继续换元。T中元素5是来自S3,让5换出其原代表3,因3∈S6,所以让3作S6的代表,得SDR={1(S1),4(S2),5(S3),7(S4),2(S5),3(S6)}。 下面给出此算法的形式化描述,为此先定义如表1所示的三个数据结构 表1 算法1中所需数据结构 算法1 寻找集合系S1,S2,…的相异代表组 SDR(S1,S2,…) 输入:集合系S1,S2,… 输出:此集合系的相异代表组sdrep。 1.IFai∈Si&& ai≠aj(i=1,2,…;j=1,2,…,i-1) 2.sdrep(i)←ai; 3.ELSEsdrep(i)=Rep_exch(Si); FunctionRep_exch(St) 输入:St 输出:找出St的代表 1.T←St;∥SupposethattheTisasequentialset。 2.FOReachelementbiinT 3.IFbi∈sdrep 4.findoutthesetSiwhoserepresentativeisbi 5.T←Si-T; 6.ELSE 7.IFbi∈St 8.RETURNbi; 9.ELSE 10.findoutthesourceset,saySj,ofbi; 11.findouttherepresentative,saybu,ofSjfromsdrep; 12. bi∈bu;GOTO3。 13.END 14.END 15.END 随着基于大数据、数据中心网络的云计算模式的成熟,对交换结构的端口数量、交换容量、交换延迟及能耗等的要求越来越高。这些性能需求不仅对硬件结构带来转型的压力,而且对分组交换的控制算法的有效性也提出了更高的要求。基于Clos网络的多级交换结构具有良好的模块性及可扩展性,因此在交换结构面临性能压力时再次受到了业界的关注,但目前面向此结构的分组控制算法由于自身的交换模式不能很好地满足云计算所致的性能需求,而且它也只能在某些流量模式下效果显著,如均匀流量模式。 本文提出基于相异代表组的分组控制算法是针对无缓存Clos交换结构。该算法将分组的交换分成两步完成,第一步实现输入端口与输出端口间的配对;第二步实现为配对成功的输入-输出对寻找合理的路由路径。这样能有效避免在多级之间来回产生大量的仲裁信息,从而提高吞吐率降低延迟。 [1]CLOSC.Astudyofnon-blockingswitchingnetworks[J].Bellsystemstechnicaljournal,1953,32(3):406-424. [3] 刘晓锋,吴亚娟.Clos交换网络的一种基于矩阵分解的路由指派算法[J].西华师范大学学报(自然版),2015,36(4):404-410. [4] HOPCROFT J E, KARP R M. An n5/2algorithm for maximum matching in bipartite graph[J]. SIAM Journal on Computing,1973,2(4):225-231. [5] MCKEOWN N,MEKKITTIKUL A,ANANTHARAM V,et al.Achieving 100% throughput in an input-queued switch[J].IEEE Transactions on Communications,1999,47(8):1260-1267. [6] OKI E,JING Z G,CESSA-R R,et al.Concurrent round-robin-based dispatching schemes for Clos-network switches[J].IEEE/ACM Transactions On Networking,2002,10(6):830-844. [7] ANDERSON T E,OWICKI S S,SAXE J B,et al.High-speed switch scheduling for local-area networks[J]. ACM Transactions on Computer Systems,1993,11(4):319-352. [8] MCKEOWN N.The iSLIP scheduling algorithm for input-queued switches[J].IEEE/ACM Transactions on Networking,1999,7(2):188-201. [9] BCHAO H J,JING Z G,LIEW S Y.Matching algorithms for three-stage bufferless Clos network switches[J].IEEE Communications Magazine,2003,41(10):46-54. [10] PUN K,HAMDI M.Distro:a distributed static round-robin scheduling algorithm for bufferless Clos-network switches[C]//Proc.of IEEE Globecom,Taipei:2002,3:2298-2302. [11] MANN H B,RYSER H J. Systems of distinct representatives[J].The American Mathematical Monthly,1953,60(6):397-401. [12] HALL M. An algorithm for distinct representatives[J].The American Mathematical Monthly,1956,63(10):716-717. A Routing Control Algorithm Based on SDR for Unbuffered Clos-network Switches LIU XiaoFeng (College of Computer Science,China West Normal University,Nanchong Sichuan 637009,China) The Clos-network switch,as a typical representative of multi-stage switching architectures,is gaining considerable research interest and momentum again both from academia and industry in cloud-computing era with the characteristics of big data and data center networks.However, most existing control algorithms (or scheduling algorithms) applied to Clos-switches cannot well satisfy the performance requirements of low latency and low power consumption in big data and data center networks.Therefore, according to the scheduling process of packets in Clos-switches,a control algorithm based on system distinct representative (SDR) is proposed in this paper to dispatch deferent central switching module (CM) for each arrived packet so as to realize non-broking switching.Moreover, the theoretical proof and an example are provided on the validity of the proposed control algorithm.Since the control algorithm does not need to exchange much arbitration information,it can effectively reduce the switching delay and improve the throughput. packet switching;system distinct representative (SDR);Clos-network;control algorithm 1673-5072(2016)03-0354-07 2016-01-18 基金项目:西华师范大学博士启动基金项目(15E013,11B026);四川省教育厅重点项目(16ZA0174) 作者简介:刘晓锋(1972—),男,重庆石柱人,副教授,博士,主要从事计算机网络体系条结构、路由与交换等相关研究。 通讯作者:刘晓锋,E-mail:xhxfliu@163.com TP393 A 10.16246/j.issn.1673-5072.2016.03.022
4 结 论
