利用二元函数性质来刻画集值映射的单调性
2016-12-24龙天友叶明露
龙天友,叶明露,李 军
(西华师范大学 数学与信息学院,四川 南充 637009)
利用二元函数性质来刻画集值映射的单调性
龙天友,叶明露,李 军
(西华师范大学 数学与信息学院,四川 南充 637009)
首先回顾了集值映射和二元函数的几种单调性,包括单调、严格单调、强单调、伪单调、拟单调以及弱单调,并定义了二元集值函数的这几种单调性,同时举出大量例子说明这些单调性之间的关系。最后,利用二元实值函数和二元集值函数的六种单调性分别刻画了集值映射的六种单调性。
集值映射;二元函数;单调性条件
0 引 言
许多数学模型,包括优化问题、多目标优化问题、变分不等式问题、不动点问题、互补性问题和非合作Nash均衡问题等,都可以通过均衡问题来进行表达:找到向量x*∈S,使得
f(x*,y)≥0,∀y∈S,

变分不等式理论被广泛地运用于各个领域,如经济学、物理学、工程学、优化与控制、运输业等[4,5]。像数学规划问题中的凸性一样,单调性在求解变分不等式时起到了非常重要的作用。为了研究变分不等式,Karamardian和Schaible在文献[6]中引入了各种单调映射。在文献[7]中,Crouzeix,Marcotte和Zhu引入了单调加映射并利用切平面方法证明了求解变分不等式解的迭代算法的收敛性。Bigi和Passacantdo在文献[8]中,给出了12种二元函数的单调性,并且概括了他们之间的关系。特别地,还分别对变分不等式和线性均衡问题进行了详细地描述。那么,由此我们联想到了利用二元函数的单调性来刻画集值映射的单调性。
本文的主要目的是研究集值映射的单调性,并通过构造二元函数和二元集值函数来刻画集值映射单调性的一些条件。为了得到这些条件,我们首先给出了集值映射的单调性, 二元函数和二元集值函数单调性定义,并且给出了这些单调性之间的蕴涵关系,还举出了一些反例来证明他们之间的反蕴涵关系不成立。然后建立起了它们之间的一些等价关系。
本文的安排如下,在第1节中,我们回顾一些相关的概念和结论来作为我们理论分析的主要工具,并举出几个相关例子。在第2节中,我们通过构造二元函数和二元集值函数来刻画集值映射几类单调性的等价条件。
1 集值映射和二元函数的单调性及例子
我们首先回顾一些相关的概念和结论来作为我们理论分析的主要工具。

我们首先给出集值映射的单调性定义:

x,y∈S,tx∈F(x),ty∈F(y)⟹〈ty-tx,y-x〉≥0
成立,则称F在S上单调;若
x,y∈S,x≠y,tx∈F(x),ty∈F(y)⟹〈ty-tx,y-x〉>0
成立,则称F在S上严格单调;若存在常数τ>0,使得
x,y∈S,tx∈F(x),ty∈F(y)⟹〈ty-tx,y-x〉≥τ‖y-x‖2


〈tx,y-x〉≥0⟹〈ty,y-x〉≥0,
则称F在S上伪单调;若对任意的x,y∈S,tx∈F(x),ty∈F(y),有
〈tx,y-x〉>0⟹〈ty,y-x〉≥0
则称F在S上拟单调;若存在常数τ>0,对任意的x,y∈S,tx∈F(x),ty∈F(y),有
〈ty-tx,y-x〉≥-τ‖y-x‖2,
则称F在S上弱单调。
由定义显然有强单调性蕴涵严格单调性,严格单调性蕴涵单调性,单调性蕴涵伪单调性,而伪单调性又蕴涵拟单调性。同时单调性也蕴涵弱单调性。但是,反过来就不一定有这样的蕴涵关系了。比如下面的几个映射:

很容易验证:映射F1单调但非严格单调,映射F2严格单调但非强单调。








f(x,y)+f(y,x)≤0

f(x,y)+f(y,x)<0

f(x,y)+f(y,x)≤-τ‖y-x‖2
成立,则称f在S上强单调。
二元函数的伪单调性、拟单调性和弱单调性定义如下:

f(x,y)≥0⟹f(y,x)≤0,

f(x,y)>0⟹f(y,x)≤0,

f(x,y)+f(y,x)≤τ‖y-x‖2,
则称f在S上弱单调。
显然,根据定义可得强单调性蕴涵严格单调性,而严格单调性又蕴涵单调性。单调性蕴涵伪单调性,伪单调性蕴涵拟单调性,单调性蕴涵弱单调性。然而,反过来同样也不一定具有这样的蕴涵关系,如下面的例子。

f(x,y)+f(y,x)=(x3-y3)(y-x)<0。

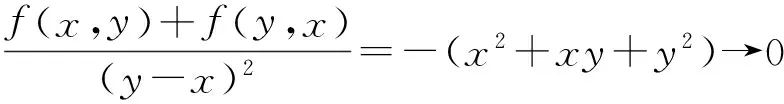


f(x,y)+f(y,x)=0


f(x,y)≥0⟹y≥x⟹f(y,x)≤0,




f(x,y)>0⟹y>x⟹f(y,x)≤0,
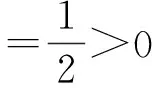

f(x,y)+f(y,x)=(y-x)2

下面,我们给出二元集值函数的几种单调性定义。






成立,则称T在S上强单调。






则称T在S上弱单调。
根据定义显然有以下蕴涵关系:强单调性蕴涵严格单调性,严格单调性蕴涵单调性,而单调性又蕴涵伪单调性,伪单调性蕴涵拟单调性,同时也有单调性蕴涵弱单调性。但是,反过来的蕴涵关系就不一定成立了。显然,当二元集值映射T只有一个元素的时候,它就是一个简单的二元函数。因此,请看下面的几个例子。

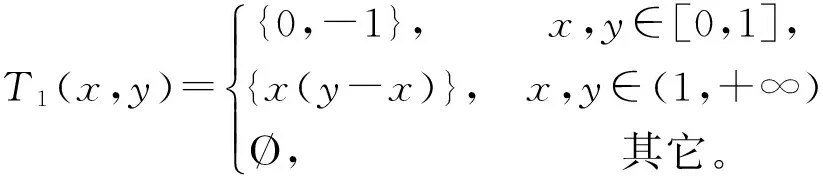
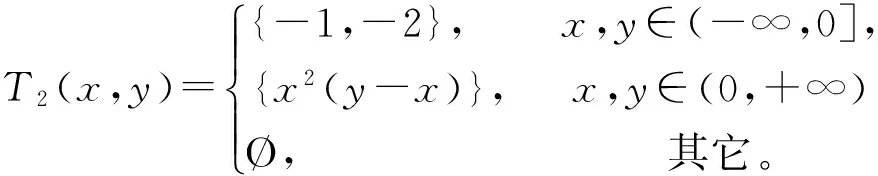
由定义易知T1单调而非严格单调,T2严格单调而非强单调。
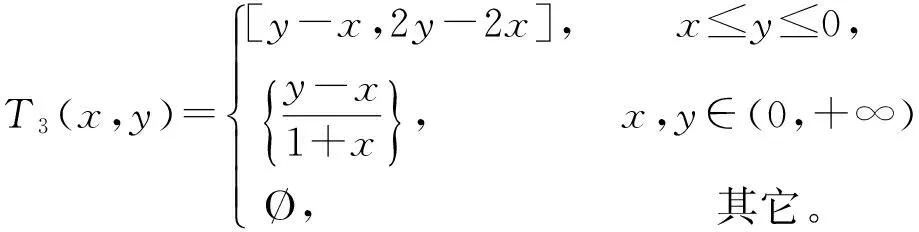
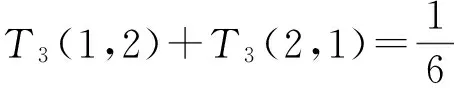
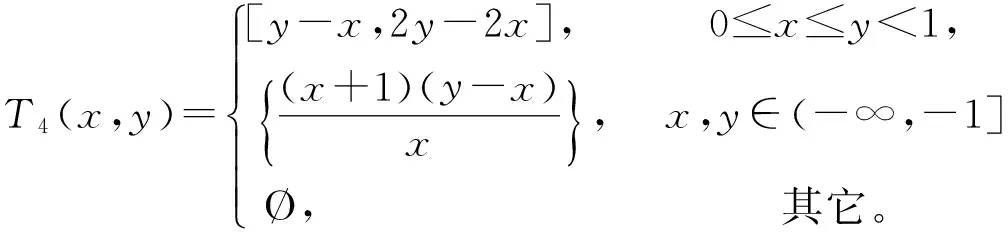


由定义易知T5弱单调。但是T5(-1,-2)+T5(-2,-1)=1,即T5不是单调的。
2 集值映射单调性的刻画

命题1 下列结论成立:
(a)F在S上单调的充要条件是:对任意的x,y∈S,有

(b)F在S上严格单调的充分条件是:对任意的x,y∈S,x≠y,有
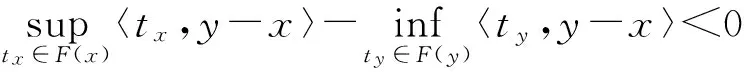
若集值映射F在S上有紧值,则必要性成立。
(c)F在S上强单调的充要条件是:存在常数τ>0,对任意的x,y∈S,有

命题2 以下结论成立:
(a)F在S上单调的充要条件是:对任意的x,y∈S,有

(b)F在S上严格单调的充要条件是:对任意的x,y∈S,x≠y,有

(c)F在S上强单调的充要条件是:存在常数τ>0,对任意的x,y∈S,有


同理可证(b)、(c)。
由此,下面我们通过构造二元函数来刻画集值映射的单调性。
定理1 对任意的x,y∈S令

(1)
则以下的结论成立:
(a)F在S上单调的充要条件是:在f上S单调;
(b)F在S上严格单调的充分条件是:f在S上严格单调;若集值映射F在S上有紧值, 则必要性成立;
(c)F在S上强单调的充要条件是:f在S上强单调;
(d)F在S上伪单调的充分条件是:f在S上伪单调; 若集值映射F在S上有紧值, 则必要性成立;
(e)F在S上拟单调的充分条件是:f在S上拟单调; 若集值映射F在S上有紧值, 则必要性成立;
(f)F在S上弱单调的充要条件是:f在S上弱单调。
证明 (a)首先证明必要性。由(1)式可得
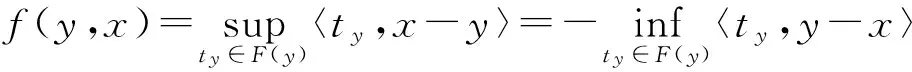
(2)
将(1)式与(2)式相加,即可得

(3)
又因为F在S上单调,则对任意的x,y∈S,由命题1(a)可得

(4)
成立,即f在S上单调。
下面证明充分性。若f在S上单调,则对任意的x,y∈S,均有(4)式成立,再由命题1(a)有F在S上单调。
(b)首先证明充分性。因为f在S上严格单调,则对任意的x,y∈S,x≠y,有f(x,y)+f(y,x)<0成立,再由(3)式即有

(5)
由命题1(b)可得F在S上严格单调。
再证明必要性。若F在S上严格单调,则对任意的x,y∈S,x≠y,有
〈tx,y-x〉<〈ty,y-x〉
成立,又因为集值映射F在S上有紧值,从而
成立。因此有(5)式成立,即f在S上严格单调。
(c)首先证明必要性。假设F在S上强单调,则存在常数τ>0,对任意的x,y∈S,tx∈F(x),ty∈F(y),有〈ty-tx,y-x〉≥τ‖y-x‖2成立,即
〈tx,y-x〉-〈ty,y-x〉≤-τ‖y-x‖2
成立,由tx和ty的任意性,对任意的x,y∈S,有

成立,即

(6)
因此f在S上强单调。
下面证明充分性。因为f在S上强单调,则存在常数τ>0,对任意的x,y∈S,使得
f(x,y)+f(y,x)≤-τ‖y-x‖2
成立。又因为

则由(6)式可得,对任意的x,y∈S,tx∈F(x),ty∈F(y),有〈ty-tx,y-x〉≥τ‖y-x‖2成立,即F在S上强单调。
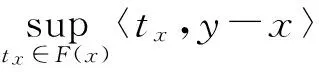

(e)与(d)证明方法类似。
(f)首先证明必要性。假设F在S上弱单调,则存在常数τ>0,对任意的x,y∈S,tx∈F(x),ty∈F(y),有
〈ty-tx,y-x〉≥-τ‖y-x‖2
成立,即
〈tx,y-x〉-τ‖y-x‖2≤〈ty,y-x〉
(7)
成立,从而

(8)
成立,即

(9)
成立,因此f在S上弱单调。
其次证明充分性。若f在S上弱单调,则存在常数τ>0,对任意的x,y∈S,都有(9)式成立,即(8)式成立,则存在常数τ>0,对任意的x,y∈S,tx∈F(x),ty∈F(y),有(7)式成立,因此F在S上弱单调。
定理2 对任意的x,y∈S令
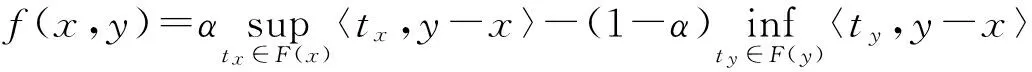
(10)
这里α∈[0,1],则以下结论成立:
(a)F在S上单调的充要条件是:f在S上单调;
(b)F在S上严格单调的充分条件是:f在S上严格单调;若集值映射F在S上有紧值,则必要性成立;
(c)F在S上强单调的充要条件是:f在S上强单调;
(d)F在S上弱单调的充要条件是:f在S上弱单调。
证明 由(10)式可得

(11)
将(10)式与(11)式相加,即可得

(12)
于是(a)— (d)的证明分别与定理1(a)— (c)和(f)的证明方法相似。
上述的二元函数都是单值的函数,下面通过二元集值函数单调性来刻画集值映射的单调性。
定理3 对任意的x,y∈S令T(x,y)=〈F(x),y-x〉,则有以下结论成立:
(a)F在S上单调的充要条件是:T在S上单调;
(b)F在S上严格单调的充要条件是:T在S上严格单调;
(c)F在S上强单调的充要条件是:T在S上强单调;
(d)F在S上伪单调的充要条件是:T在S上伪单调;
(e)F在S上拟单调的必要条件是:T在S上拟单调;
(f)F在S上弱单调的充要条件是:T在S上弱单调。
证明 (a)首先证明必要性。假设F在S上单调,由命题2(a),则对任意的x,y∈S,都有

成立,由于T(x,y)=〈F(x),y-x〉,可得

(13)
即T在S上单调。
下面证明充分性。由于T在S上单调,则对任意的x,y∈S,显然有(13)式成立。由命题2(a)可得,F在S上单调。
(b)、(c)的证明与(a)证明方法相似。


(e)的证明与(d)证明方法相似。
(f)若F在S上弱单调,则存在常数τ>0,对任意的x,y∈S,tx∈F(x),ty∈F(y),有
〈ty-tx,y-x〉≥-τ‖y-x‖2,
等价于对任意的x,y∈S,有

因此T在S上弱单调。
[1] BIGI G,CASTELLANI M,PAPPALARDO M,et al.Existence and solution methods for equilibria[J].European J.Oper.Res.,2013,227(1):1-11.
[2] BLUM E,OETTLI W.From optimization and variational inequalities to equilibrium problems[J].Math.Stud.,1994,63(1/2/3/4):123-145.
[3] FACCHINEI F,PANG J S.Finite-dimensional variational inequalities and complementarity problems[M].New York:Springer-Verlag,2003.
[4] BAIOCCHI C, CAPELO A.Variational and quasivariational inequalities applications to free boundary problems[M].New York:John Wiley & Sons,1984.
[5] HARKER P T,PANG J S.Finite-dimensional variational inequalities and nonlinear complementarity problems:a survey of theory,algorithms and applications[J].Math.Program.Series B,1990,48(2):161-220.
[6] KARAMARDIAN S,SCHAIBLE S.Seven kinds of monotone maps[J].J.Optim.Theory Appl.,1990,66(1):37-46.
[7] CROUZEIX J P ,MARCOTTE P,ZHU D L.Conditions ensuring the applicability of cutting-plane methods for soving variational inequalities[J].Math.Program.Series A,2000,88(3):521-539.
[8] BIGI G,PASSACANTANDO M.Twelve monotonicity conditions arising from algorithms for equilibrium problems[J].Optim. Methods Softw.,2015,30(2):323-337.
[9] FUKUSHIMA M.非线性最优化基础[M].北京:科学出版社,2011.
Some Characterizations of Monotonicity of Set-valued mappings By Using Properties of Bifunctions
LONG Tianyou,YE Minglu,LI Jun
(College of Mathematics and Information,China West Normal University,Nanchong Sichuan 637009,China)
In this paper,we first recall the monotonicity of set-valued mappings and bifunctions,such as monotonoicity,strict monotonicity, strong monotonicity,pseudomonotonicity,quasimonotonicity and weak monotonicity.We then define these monotonicity of set-valued bifunctions.Several examples are given to illustrate these monotonicity.We also give some new characterizations of six kinds of monotonicity of set-valued mappings by using bifunctions and set-valued bifunctions.
set-valued mapping;bifunction;monotonicity
1673-5072(2016)03-0289-08
2015-10-21 基金项目:国家自然科学基金项目(11371015); 教育部科学技术重点项目(211163); 四川省青年科技基金(2012JQ0035)
龙天友( 1990—) , 女, 四川隆昌人, 硕士研究生, 主要从事优化理论及应用研究。
李 军( 1974—) , 男, 四川旺苍人,教授,主要从事优化理论及应用研究。E-mail: junli1026@163.com
O221
A
10.16246/j.issn.1673-5072.2016.03.011
