基于星座图统计的盲载波同步算法

邱钊洋, 黄 焱, 欧阳喜

(解放军信息工程大学信息系统工程学院, 河南 郑州 450001)



基于星座图统计的盲载波同步算法

邱钊洋, 黄 焱, 欧阳喜

(解放军信息工程大学信息系统工程学院, 河南 郑州 450001)

卫星通信信号中90%以上采用相位或幅相联合调制方案,包括多进制相位键控(multiple phase shift keying，MPSK)，多进制正交幅度调制(multiple quadrature amplitude modulation，MQAM)，多进制幅相键控(multiple amplitude phase shift keying，MAPSK)等,此外短波通信、移动通信中MPSK也是最常用的信号类型之一。载波同步是信号解调中十分关键与核心的部分。针对非合作接收条件下幅相调制类信号星座图分布特性进行了深入研究,提出了一种基于星座图密度统计的载波同步算法,实现了一定信噪比条件下盲频偏消除与星座图恢复,此方案不需要预先进行调制识别,对数据量要求不高,复杂度低,抗噪性能好,可广泛应用于常规信号以及未知、猝发信号解调。仿真表明,在接近或高于解调信噪比的条件下,该方法频偏估计性能接近克拉美罗限,可应用于工程实践。

幅相调制信号; 盲载波同步; 突发信号解调

0 引 言

卫星通信中,幅相调制类(amplitude-phase modulated,APM)信号由于其频带利用率高,易于调制解调,被广泛用于各种标准。卫星数字视频广播标准(digital video broadcast-satellite, DVB-S)中采用移相键控(multiple phase shift keying, MPSK)和正交振幅调制(multiple quadrature amplitude modulation,MQAM)进行信号传输[1],DVB-S2中同时采用振幅移相键控(multiple amplitude phase shift keying,APSK)进行信号传输,并采用自适应编码调制(adaptive coded modulation, ACM)技术动态地改变调制方式。经统计,现存卫星信号中,90%以上均采用MPSK,MQAM, MAPSK等相位或幅相联合调制方式,除此之外,移动通信,短波,超短波等各频段都广泛存在APM类数字信号。

在实际的通信系统及信息对抗活动中,由于很难获取训练序列,尤其是在诸如卫星载波监视、监测、通信侦察和其他非合作接收等非协作通信中,由于没有调制类型的先验知识,盲解调和参数估计一直是一个十分重要的问题。许多文章研究了信号的调制识别和参数估计问题。全盲条件下这些方法普遍存在估计精度与算法复杂度成正比,且要求数据量足够多,信噪比足够高等,不能有效应对未知、突发信号以及可变调制类信号。星座图是APM信号最本质的特征之一,文献[2]通过统计星座点的瞬时相移的统计,实现了MPSK信号的调制阶数识别和小频偏估计,文献[3]通过对星座点统计实现了存在频偏情况下APM信号的匹配识别,文献[4]通过星座点周期性相差实现了APSK信号的小频偏估计,这些方法虽然利用了星座图特征,但性能受限于信噪比和信号类型,适应性和实用性也十分有限。本文针对非合作接收条件下的APM信号全盲解调算法进行了深入研究,提出一种基于星座图统计的盲载波同步方案,该方法避开了复杂的调制识别,抗噪性能好,复杂度低。经过仿真与实测,在同样满足解调信噪比的环境下,能够实现MPSK、MQAM、MAPSK等APM信号的全盲载波同步,频偏估计性能在符号数较少时也能逼近克拉美罗限,同时由于本文算法无需任何先验知识,对信号无区分,故其适应性、灵活性、鲁棒性大大优于目前已有算法。

1 APM信号解调流程及星座图特性

非合作条件下卫星信道中APM类通信信号的解调一般需要完成调制识别定时同步,载波同步等一系列工作。

图1 非合作接收条件下卫星信号常规解调流程
Fig.1 Conventional satellite signal demodulation process under non-cooperative reception conditions

对于APM类信号的调制识别研究已进行多年,目前大多是基于相差特征或非线性变换谱线特征等,定时同步可采用模方谱方法提取离散谱线获得符号速率信息,进而对信号进行匹配滤波,之后采用平方定时方法获得最佳采样点。载波同步是APM类信号解调中最为关键和核心的部分,一般而言,不同的调制方式对应着不同的载波同步过程,所以传统的载波同步要求必须完成精确的调制识别。目前针对该类信号载频估计主要是依靠M次方谱[5],对信号进行去调制信息后,利用单频谱线进行载频估计,这种方法的前提是必须已知信号的调制方式,且对信号的数据量、信噪比等要求较高,而非合作接收条件下,信号的调制未知且信噪比一般较低,故这种方法使用受限。而星座图作为APM类信号原始的映射特征,其分布特性可以为实现精确的载波同步提供十分重要的信息。

如图2(a)所示,载波频偏得到消除时,信号定时后的星座图呈现明显的聚集特性,这是进行判决的基础,而存在一定频偏时,如图2(b)所示,星座点将不断的积累相差,最终呈现出环状特性。仅含频偏情况下,3类信号的标准星座图环状特性如表1。

可见,幅相调制类信号的星座图都是由这些分布在不同圆环上的星座点构成。利用这种特征,通过对星座图分布进行统计,构造统计量来衡量星座图的聚集特性,可以实现性能良好的频偏估计。本文正是基于此,对含频偏星座图进行去频偏处理,从而实现信息星座图的还原,进而实现全盲解调。

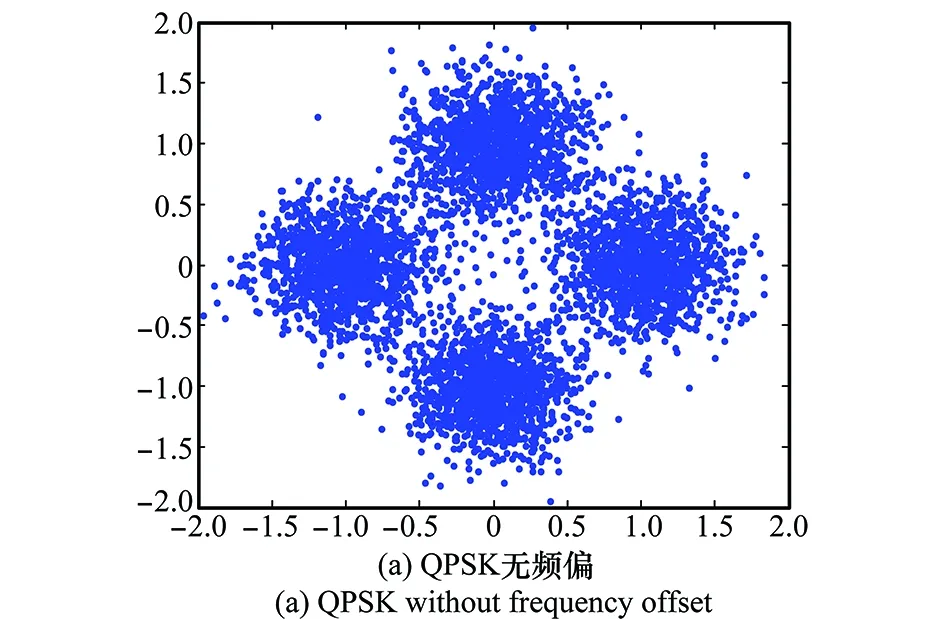
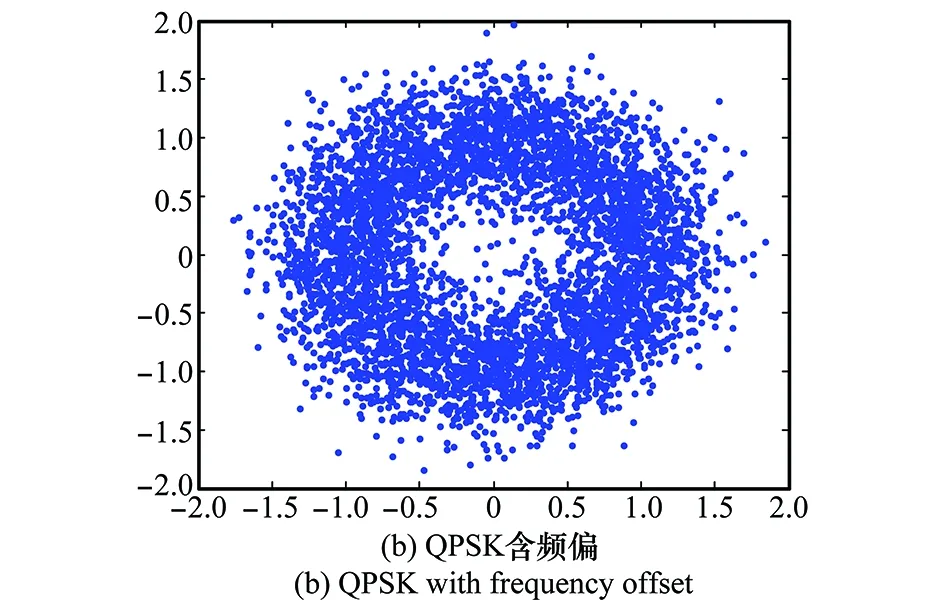
图2 APM信号的星座图分布特性Fig.2 Constellation distribution of APM signal

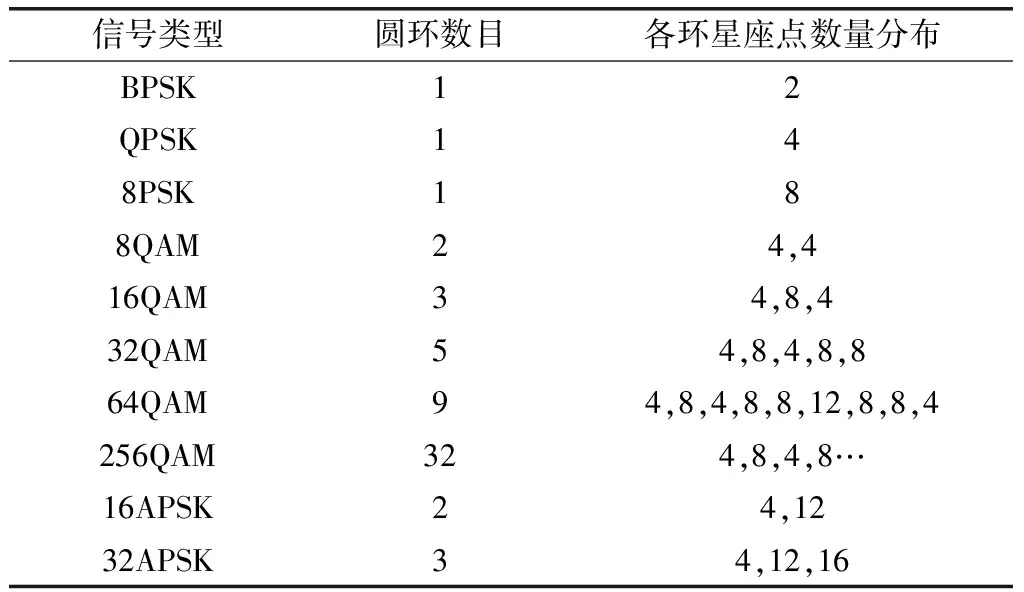
信号类型圆环数目各环星座点数量分布BPSK12QPSK148PSK188QAM24，416QAM34，8，432QAM54，8，4，8，864QAM94，8，4，8，8，12，8，8，4256QAM324，8，4，8…16APSK24，1232APSK34，12，16

2 算法流程

2.1 星座图获取

幅相调制信号的复基带模型可以表达为

(1)

式中，Δf为载波频偏;φ为载波初相;T为符号周期;g(t)是等效的信道滤波器,包括成型滤波器、信道,匹配滤波器等;an为能量归一化后的符号序列;v(t)为高斯白噪声。

设M为调制阶数,对于PSK类信号:

an=ej(2i+1)π/M,i=0,1…,M-1

(2)

对于QAM类信号:

(3)

对于APSK类信号:

(4)

式中,rk为第k个圆周半径;nk为第k个圆周的星座点数量;ik为第k个圆周上的第i个星座点;θk为第k个圆周的初始相偏。

接收信号后对信号做welch谱,从中直接粗估出载频,进行下变频。对下变频后的信号进行模方谱运算,在符号速率处会出现离散谱线,检测谱线位置获得信号传输的符号速率,据此设计根升余弦滤波器,滚降系数一般为0.35,进行匹配滤波,以提高信号定时时刻的信噪比。

为了获得最佳抽样时刻以消除码间串扰提高信噪比,需估计信号的初始时延,本文采用Oerder和Merl 提出的时延估计算法[6],如式(5):

(5)

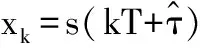
值处理[7],即可获得传输信号的含频偏星座图,均衡[8]可减弱星座图中的多径效应,使其模值更为收敛。APM信号定时同步流程见如图3。

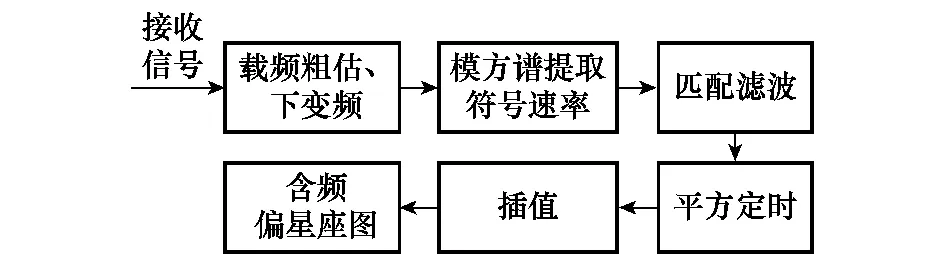
图3 APM信号定时同步流程Fig.3 APM signal timing synchronization process

2.2 星座图分布统计

2.2.1 环数估计

对星座图上映射点进行取模操作,可以得到其幅度分布。理想无噪声,仅存在频偏的情况下,MPSK类星座图会呈现一个圆环,模值即为该圆环的半径,即各点模值相等。含噪声情况下,PSK类信号将呈现出图4(a)所示的离散的圆环状,此时星座点模值直方图将呈现图4(b)所示类高斯分布,均值为圆环的半径,方差为环状星座点的方差,该方差与噪声方差呈正相关。

对于QAM类方形星座图和APSK类多环状星座图而言,若存在载波频偏,星座图旋转形成多个环,如图5所示,有噪声情况下对其模值进行直方图统计将呈现多个类高斯特性。

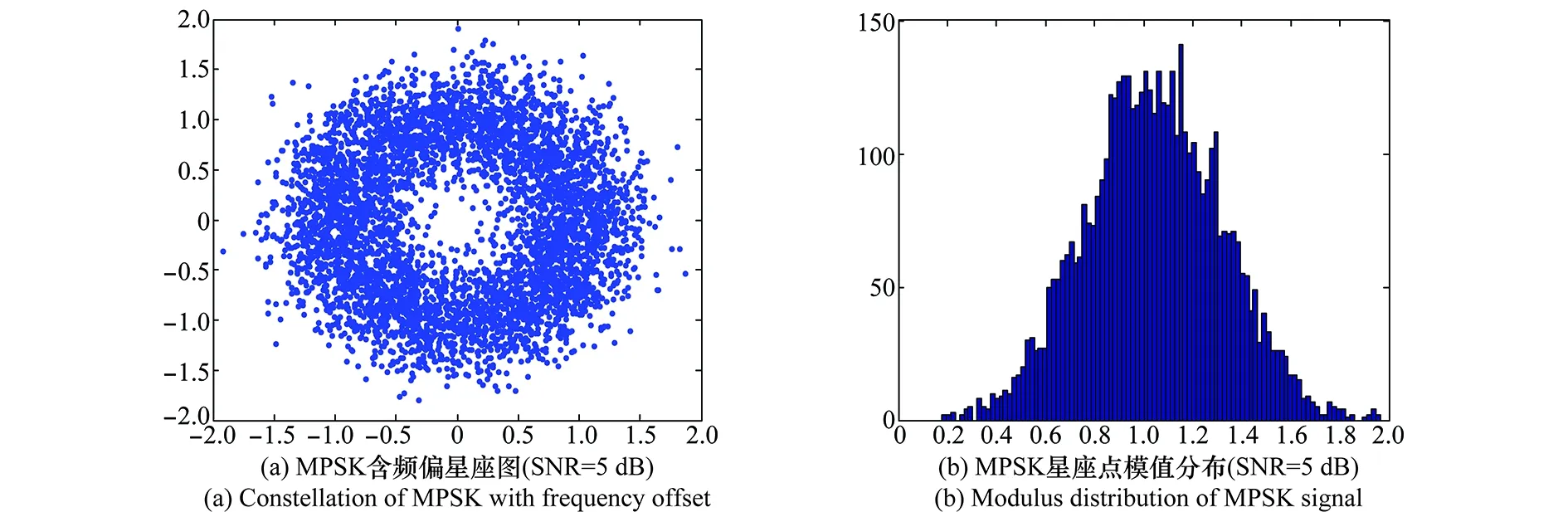
图4 MPSK含频偏星座图及其模值分布Fig.4 MPSK constellation with frequency offset and its modulus distribution

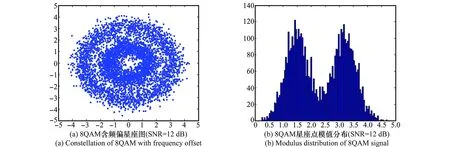
图5 8QAM含频偏星座图及其模值分布Fig.5 8QAM constellation with frequency offset and its modulus distribution

经过以上理论分析可得APM信号的星座图特征。由于应用背景为高斯白噪信道,故含频偏星座图上星座点的环状分布特性,在数学上可理解为星座点幅值的概率密度是多个高斯分布的混合,由于各环上星座点的数量可能不同,统计意义上反映到模型中即各高斯分布的权值不同。

文献[3]说明了这一点,并进一步证明了各环高斯分布的方差:

(6)

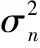
设x=[x0,x1,…,xN]为定时同步后的星座点幅值,由以上分析,在高斯白噪信道下,这些星座点幅值的概率密度应满足(7)式所示的混合高斯分布:

(7)

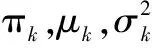
常用于图像处理、语音识别、聚类分析中的高斯混合模型(Gaussian mixture model, GMM)是描述这一问题有力数学工具[9-10]。GMM模型通常采用期望最大化(expectation maximization, EM)算法进行求解[10],其本质是寻找模型参数θ使似然函数L(θ)最大化:

(8)

EM算法求解过程中需要对高斯分布的数量进行设定,本文对此进行动态的寻优,即从最大可能的聚类数目(对应所有的星座图,一般最多有10种模值)开始向下搜索,对1～10每一种可能的聚类数目分别求解似然值,选取似然值最大者作为估计的聚类数目。即聚类环数估计值:

(9)

由此采用GMM模型进行无监督聚类,可以通过迭代求解获取各聚类环半径信息,为下文的星座点密度统计提供参数。

2.2.2 聚类环上星座点密度分布统计

幅相调制信号星座图在无频偏的稳定态下呈现局部聚集特性,由此本文提出对星座图的各聚类环进行均匀分块,获得其局部星座点密度统计,从而得到各环的密度分布直方图,有频偏情况下,各环上星座点密度相对均匀,无明显峰值和谷值。无频偏情况下,各环的星座点将均匀呈现若干个聚合点,每个聚合点附近呈高斯分布。设M为单环均匀分块数,Ri为第i个聚类环半径,ri为第i个聚类环上分块圆半径,oi,j为第i个聚类环上第j个分块圆圆心。分块圆半径相等,为保证分块圆之间互不重叠且覆盖整个单环,如图6所示,可令:

(10)

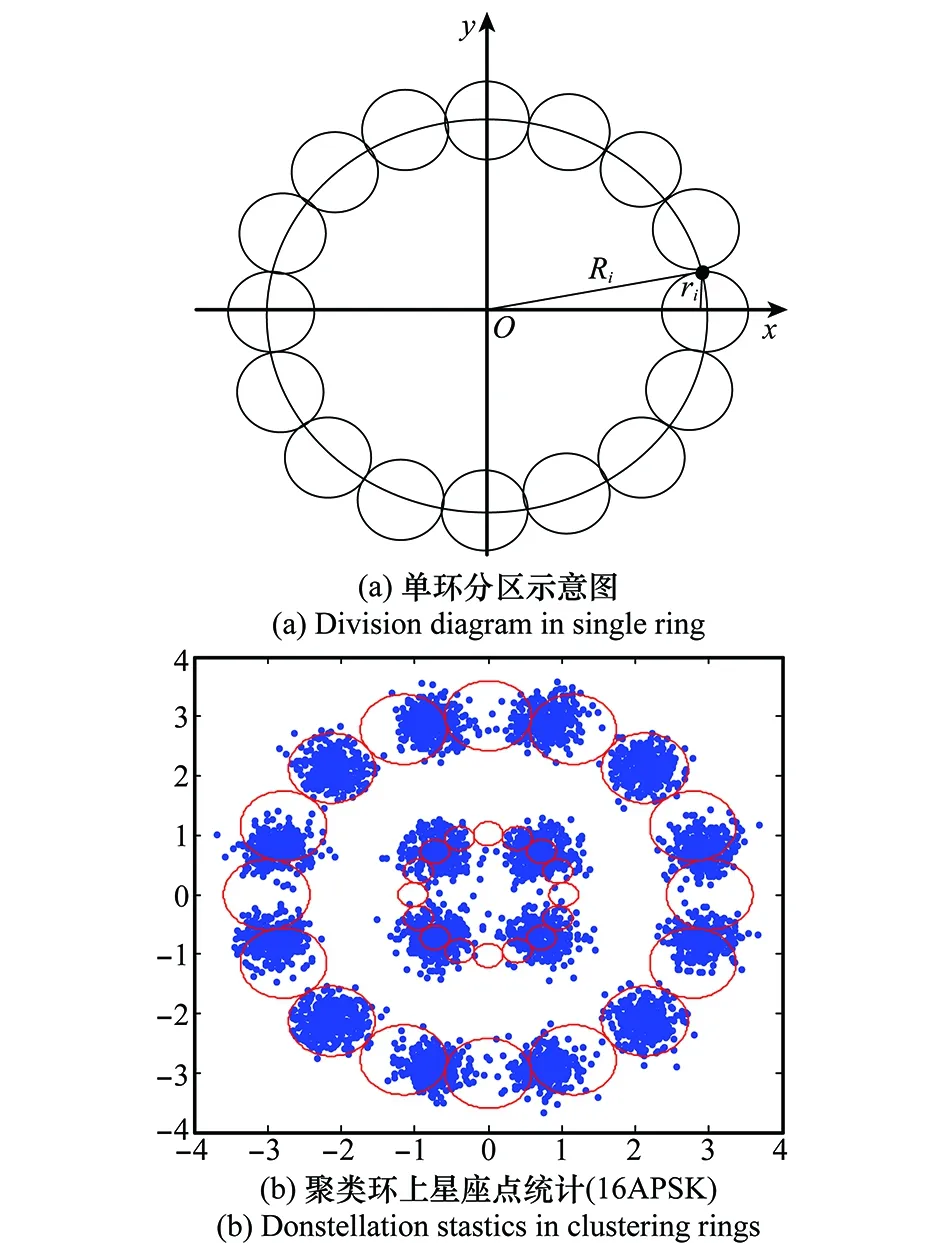
图6 聚类环分区及星座点统计示意图Fig.6 Schematic diagram of clustering ring partition and constellation point statistics

2.2.3 统计量构造

无频偏时,聚类环上星座图密度呈现图7(b)所示的多个高斯分布特性,含频偏时,星座点分布均匀,密度直方图基本稳定,见图7(a)。

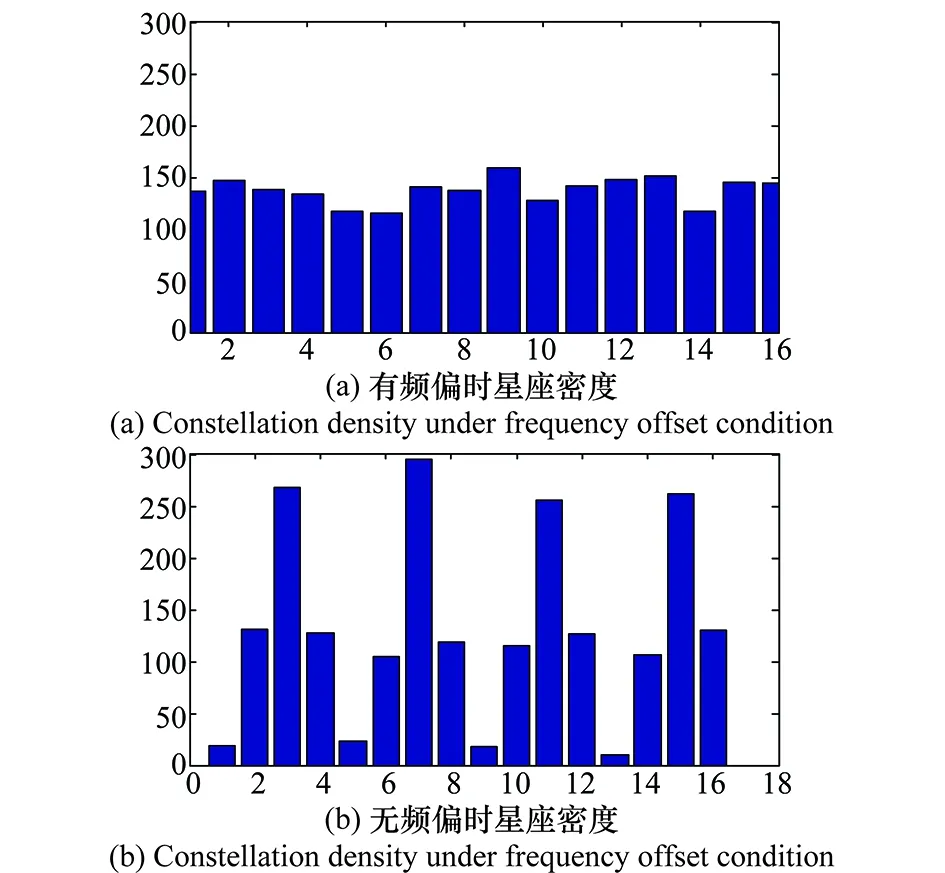
图7 各分区星座点数量统计Fig.7 Number of the partition constellation point

构造统计量对星座密度直方图进行描述,是衡量信号去频偏效果的关键。本文选用峰谷比(peak-to-valley ratio,PVR)对单环上密度直方图的不同分布进行描述,选用平均峰谷比(mean peak-to-valley ratio, MPVR)对整体星座图密度进行描述。用PVRi表示第i个聚类环上的峰谷比。令NUM(i,j)为落入第i个聚类环上第j个分块的星座点数目,其中i=1,2,…,R,j=1,2,…,M,其中R表示聚类环数目。则:

将第i个聚类环上NUM(i,j)按照从大到小的顺序排列得NUMsort(i,j),依次选取m个最大值,m个最小值,得到第i个聚类环的峰谷比定义:

(11)

为说明PVRi统计量的有效性,其与信号高斯性的关系曲线如图8所示:

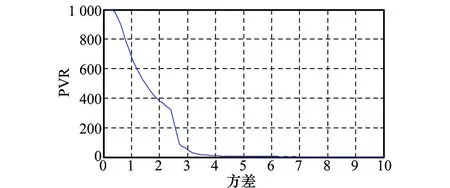
图8 星座密度直方图PVR与高斯分布方差的关系曲线Fig.8 Relationship between PVR and the Gauss curve sign density histogram distribution variance

图8为典型的多个不同均值,相同方差的高斯分布混合的条件下的峰谷比随着高斯分布方差的变化曲线,这种模型条件与星座图的密度分布特征最为接近。由图8可见,曲线是单调的,即信号的高斯性越明显(方差小,偏离均匀分布),峰值与谷值的比越大,由此,可用峰谷比作为衡量星座图聚集效果的统计量。

结合图7,当无频偏时,聚类环上直方图的高斯型较好,PVRi最大,当存在频偏时,聚类环上星座点将呈现接近均匀分布,PVRi最小。

选取各聚类环上星座点密度分布直方图峰谷比的平均值作为整个星座图的聚集特性的描述:

(12)

2.3 频偏消除与星座图恢复

2.3.1 频偏估计范围

算法的有效性建立在无频偏时星座图的最佳聚集特性之上,故星座的旋转对称性将决定本文算法对频偏的有效估计范围。经统计,幅相调制类信号的旋转对称性如表2所示。

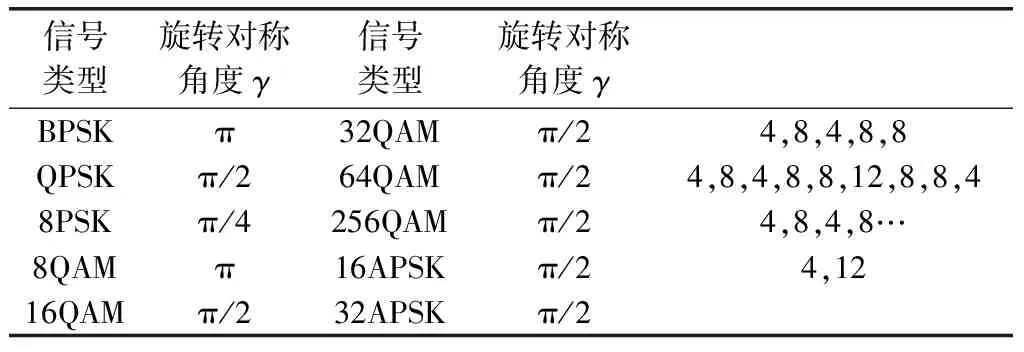
表2 常见幅相调制类信号星座旋转对称特性

根据表2星座的旋转对称性,可推得算法对信号频偏的有效估计范围为[-γ/4πTs,γ/4πTs],这是非数据辅助(non data-aided, NDA)频偏估计算法的最大估计范围。

表3中M′表示去调制阶数,N′ 表示与观测数据长度有关的量,一般取N′=N/2。对比可见,本文算法在估计范围上具有明显优势。

表3 不同频偏估计算法估计范围比较

2.3.2 频偏搜索

根据构造统计量的单调特性,我们可以根据粗估精度,设定一定的频偏区间,进行搜索,每次迭代中计算星座图各聚类单环上的星座图密度直方图峰谷比,对各单环求平均,从而得到频偏与星座图聚类环平均峰谷比的关系曲线,见图9。

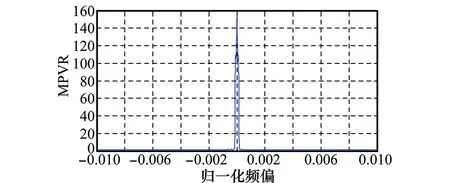
图9 归一化频偏迭代值与MPVR关系曲线Fig.9 Curve of normalized frequency offset value iteration relationship with MPVR

由星座图的频偏特性,当符号数较多时,微小的频偏也将对星座图的聚集特性产生重大的影响,使其在每个旋转单环上都趋于均匀分布,无频偏时,每个聚类单环峰均比理论上同时达到最高,故采用峰谷比可有效搜索出真实的频偏值,进而实现盲载波同步。

(13)

式中,fi为第i次迭代频偏值。

2.3.3 参数选取

本文算法的性能很大程度上取决于单环分块个数M,当信噪比达到或超过一定的值时,估计性能反而会下降,这是由于聚类环上分块数目的限制引起的,当频偏较小时,由于切分的小分块有一定面积,且符号数量有限,同一符号的星座点在一定的频偏范围内不能越过统一分块圆,此时PVR统计量将不发生变化,从而出现图10(a)所示平顶现象。

理想无噪声情况下,给定单环分区数目M,符号个数L,考虑一个分块区间能容纳的频偏范围,平顶频率区间的长度Δf可以用式(14)表示:

(14)

对此,可在平顶范围内采取增大M(分块数目)的方法,缩小分块面积,随着分块面积的减小,平顶现象将得到有效抑制,见图10(b)。此时随着信噪比的提高,频偏估计性能将继续提高。对此,算法可先设置较小的M值,随后检测平顶现象,若存在,则在平顶区间内增大M值进行搜索,直至平顶现象得到消除。

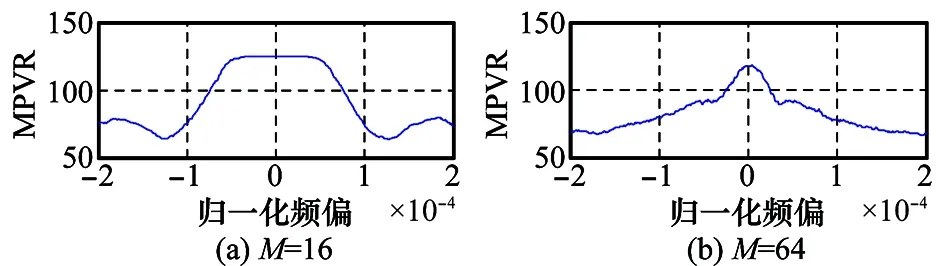
图10 低阶调制信号高信噪比情况下MPVR平顶现象Fig.10 Flat MPVR phenomenon of low order modulation signal with high SNR

2.4 非合作接收条件下盲载波同步算法与信号解调流程

据上文分析,设计如图11所示的非合作接收条件下盲载波同步与解调流程。

步骤 1 对接收信号进行welch谱估计,利用幅相调制类信号频谱的对称性,采用频率居中法[14]粗估载频,进行下变频。

步骤 2 进行符号速率估计,所有的幅相调制类信号的符号速率估计均可通过循环谱或模方谱等方法,估计精度较高。获得符号速率信息后对低通信号进行匹配滤波,计算时延,获得最佳抽样时刻,对信号进行抽样(过采倍数较低时需要先进行插值再抽样),获得含频偏星座图。

步骤 3 对含频偏星座图进行取模处理,用EM算法迭代求得GMM聚类参数,获得聚类环个数及半径等信息。

步骤 4 根据载频粗估精度设定频偏搜索区间,将信号按照设定的频偏值处理后,然后统计该频偏下各聚类环上峰谷比,求其均值。

步骤 5 检测平均峰谷比随频偏变化曲线是否存在平顶效应,若存在,在平顶区间内增大单环分块个数M,重复步骤4,若不存在,选择平均峰谷比最大时对应的频偏设定值,就是接收信号的真实频偏估计。

步骤 6 对信号进行去频偏处理后,获取稳定的星座图后,可以对其进行模板匹配,获取其调制方式,对照相关协议及映射规则,可以实现信息比特流的恢复, 或者获得软信息,进行后续的软信道译码。

图11 非合作接收条件下盲载波同步与解调流程Fig.11 Blind carrier synchronization demodulation process under non-cooperative reception conditions

3 仿真实验

实验分别选取3类信号,进行500次蒙特卡罗仿真。

实验 1 信号调制类型为QPSK,符号个数为L(500、1 000、2 000),过采倍数为4,根升余弦成形,成形系数α=0.35。选取单环分块个数初始值M=16。相对符号速率的归一化频偏的搜索区间为[-0.01 0.01]。同时采用ML—补零M次方谱法在(L=500)时仿真对比。

从图12中可以看出,对于低阶调制信号,符号数较少时估计精度也能十分接近克拉美罗限[15],相同数据量下效果优于传统的M次方谱法,同步理想。

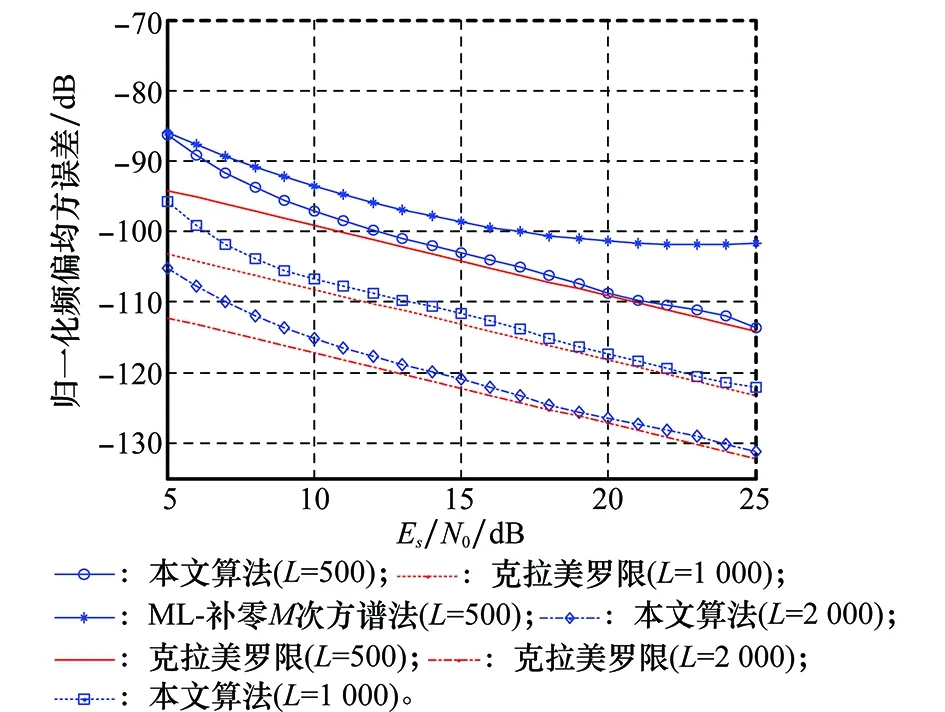
图12 QPSK载波频偏估计性能Fig.12 Performance of estimation in QPSK

实验 2 信号调制类型为16APSK,符号个数为L(500、1 000、2 000),过采倍数为4,根升余弦成形,成形系数α=0.35。选取单环分块个数初始值M=16。相对符号速率的归一化频偏的搜索区间为[-0.01 0.01]。同时采用ML—补零M次方谱法在(L=500)时仿真对比。

从图13可以看出,对于APSK类高阶信号而言,信噪比较低时,算法性能退化明显,这是由于低信噪比下,星座图的分布聚集性将受到严重干扰甚至被噪声彻底掩盖,当随着信噪比逐渐提高时,随着星座图的局部聚集性逐渐凸显,算法性能迅速提高,数据量相同时,与M次方谱法(选取12次方)对比,效果优于后者。

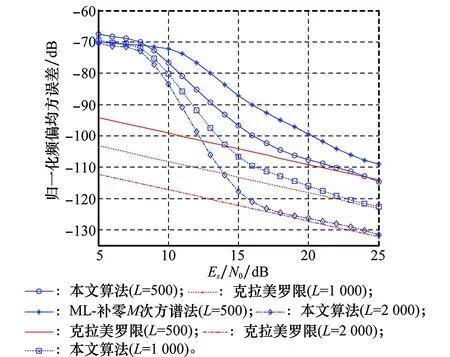
图13 16APSK载波频偏估计性能Fig.13 Performance of estimation in 16APSK

实验 3 信号调制类型为64QAM,符号个数为L(500、1 000、2 000),过采倍数为4,根升余弦成形,成形系数α=0.35。选取单环分块个数初始值M=16。相对符号速率的归一化频偏的搜索区间为[-0.01 0.01]。同时采用ML—补零M次方谱法在(L=500)时仿真对比。

从图14可以看出,对于64QAM类更高阶更复杂的信号而言,算法的性能同样稳定。低信噪比下性能的退化依然归因于星座图受到严重的噪声干扰而乱序,同样当信噪比条件达到星座图开始聚集时,算法性能将快速收敛于克拉美罗限。而从图中可以看出相同数据量,低信噪比下,算法的性能不如M次方谱法,这是由于星座图的混乱,导致性能下降,对于方形星座的高阶QAM信号,M次方谱法(选取4次方谱)在低信噪比下更有优势。当64QAM信号信噪比高于20 dB时,本文算法的精度超过M次方谱,说明在满足解调信噪比的前提下其能较好的克服M次方谱法中存在的分辨率难以提高导致的精度差等问题。

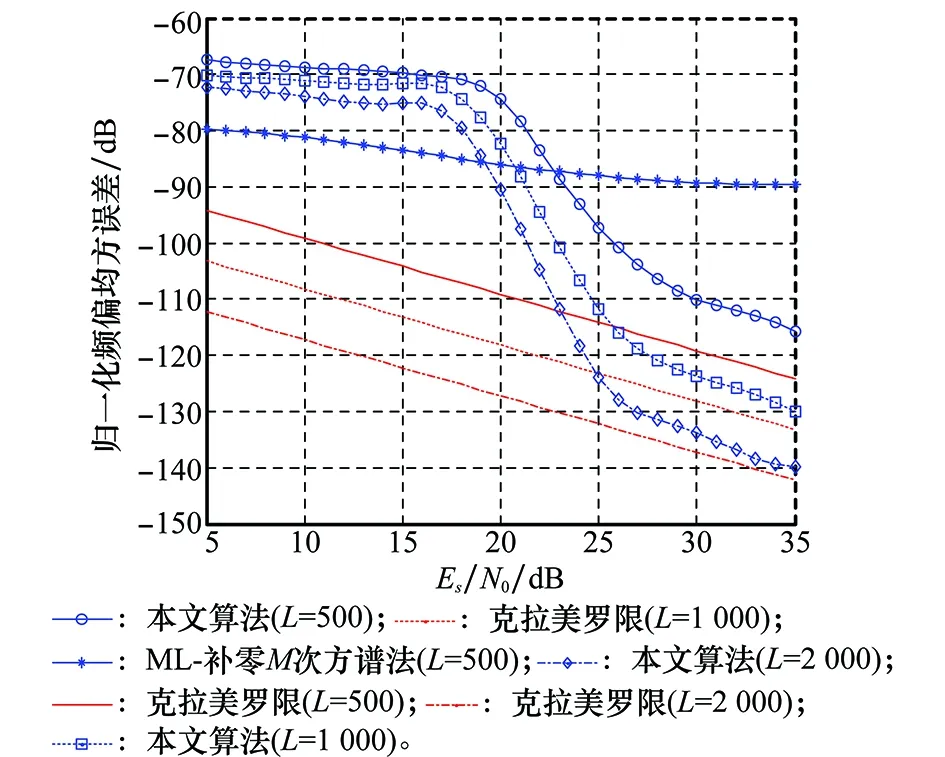
图14 64QAM载波频偏估计性能Fig.14 Performance of estimation in 64QAM

通过对恢复过程的分析,高斯混合模型的引入主要是为了识别含频偏情况下星座图的环状分布。考虑到本文所选择的星座图恢复衡量指标——各环上星座图密度分布直方图平均峰谷比,由于各环的峰谷比理论上在同一时间达到最大值,而稍有残余频偏各环的峰谷比特性将集体恶化,故可分析得本文算法对高斯混合模型的分类结果的鲁棒性较强,即无论聚类的结果是否完全正确,甚至偏差较大,只要有一个聚类环识别正确,算法均可通过比较峰谷比搜索到精确的频偏值,噪声是影响GMM模型聚类效果的主要因素,该算法对聚类的精度要求不高,即反映了其优良的抗噪性能,仿真实验结果证明了以上分析,从实验结果看,算法应用的不同信号全盲星座图恢复的信噪比门限基本等于或低于信号解调所需的信噪比,说明了算法的实用性。

频偏搜索策略主要是在频偏区间内均匀搜索,复杂度与精度成正比,考虑到频偏区间搜索时,每两次搜索之间互相独立,故可采用并行运算的思路解决复杂度问题。

4 结束语

本文提出了一种非合作接收条件下幅相调制信号的全盲载波同步算法,该算法避开了复杂的调制识别工作,充分利用幅相调制类信号星座图的特点,实现了全盲条件下频偏消除,相较于传统算法,其灵活性,适应性和抗噪性能有明显优势,适合卫星信号盲解调,尤其是未知猝发信号的盲解调。

[1] Reimers D I U.Digital Video Broadcasting (DVB)[M]∥Digital video broadcasting Artech House,1999:104-110.

[2] Wan X H, Luo W Z, Luo L Y. Blind carrier frequency estimation for MPSK signal[J].JournalofElectronicsandInformationTechnology, 2008, 30(5):1148-1150. (苑小华, 罗武忠, 罗来源. MPSK信号载波频率盲估计[J]. 电子与信息学报, 2008, 30(5): 1148- 1150.)

[3] Liao C H, Tu S L, Wan J. An anti-frequency-offset algorithm for modulation recognition of satellite amplitude-phase modulated signal[J].JournalofElectronicsandInformationTechnology, 2014, 36(2):346-352.(廖灿辉, 涂世龙, 万坚. 一种抗频偏的卫星幅相调制信号识别算法[J]. 电子与信息学报, 2014, 36(2):346-352.)

[4] Hu J M, Liu A J, Guo D S.Algorithm of carrier frequency offset estimation based on APSK cyclical phase offset[J].MilitaryCommunica-tionTechnology,2013,34(1):7-12.(胡景明,刘爱军,郭道省. 基于APSK信号周期性相差的载波频偏估计算法[J]. 军事通信技术, 2013, 34(1):7-12.)

[5] Zhao L. Automatic recognition based on spectrum feature for common used modulations[J].JournalofChinaAcademyofElectronicsandInformationTechnology, 2012, 2(2): 182-185.(赵岚. 基于谱线特征的调制方式自动识别方法[J]. 中国电子科学研究院学报,2012,2(2): 182-185.)

[6] Oerder M, Meyr H. Digital filter and square timing recovery[J].IEEETrans.onCommunications, 1988, 36(5):605-612.

[7] Farrow, C W. A continuously variable digital delay element[C]∥Proc.oftheIEEEInterna-tionalSymposiumonCircuitsandSystems, 1988:2641-2645.

[8] Yang J, Werner J J, Dumont G. The multi modulus blind equalization and its generalized algorithms[J].IEEEJournalonSelectedAreasinCommunication, 2002, 20(5):997-1015.

[9] Ou K J. Study on image segmentation based on gaussian mixture model[D]. Beijing:Beijing Jiaotong University,2015:11-13.(欧垚江. 基于高斯混合模型的图像分割的研究[D].北京:北京交通大学, 2015:11-13.)

[10] Fu Q. The study of GMM-based language identification[D].Hefei:University of Science and Technology of China,2009:15-21.(付强. 基于高斯混合模型的语种识别的研究[D]. 中国科学技术大学, 2009:15-21.)

[11] Luise M, Reggiannini R. Carrier frequency recovery in all-digital modems for burst-mode transmissions[J].IEEETransactionsonCommunications, 1995, 43(2):1169-1178.

[12] Fitz M P. Further results in the fast estimation of a single frequency[J].IEEETrans.onCommunications, 1994, 42(234): 862-864.

[13] Tretter S A. Estimating the frequency of a noisy sinusoid by linear regression[J].IEEETrans.onInformationTheroy, 1985, 31(6): 823-835.

[14] Liu S L. Modulation recognition and parameter estimation of MPSK signals[D]. Beijing: Beijing University of Posts and Telecommunications,2015.(刘少林. MPSK信号调制方式识别与参数估计[D]. 北京邮电大学, 2015：20-21.)

[15] D’Andrea A N. The modified Cramer-Rao bound and its application to synchronization problems[J].IEEETrans.onCommunications, 1994, 42(2): 1391-1399.

Blind carrier synchronization algorithm based on statistical constellation

QIU Zhao-yang, HUANG Yan, OUYANG Xi

(InstituteofInformationSystemEngineering,InformationEngineeringUniversityofPLA,Zhengzhou450001,China)

More than 90% of the signal in the satellite channel use phase or amplitude and phase united modulation scheme including MPSK, MQAM, MAPSK, etc. In shortwave communications and mobile communications, MPSK is also one of the most common signal types in addition. Carrier synchronization is crucial and the central part in signal demodulation. A thorough research on the constellation distribution of amplitude-phase modulated (APM) signal is conducted under the condition of non-cooperation receiving, and then a synchronization algorithm is proposed based on constellation density statistics which realizes the blind elimination of carrier offset and constellation recovery. This algorithm does not require a modulation recognition in advance, less amount of data, low complexity, good anti-noise performance, and it can be widely used in conventional signals and unknown, burst signal demodulation. The simulation results show that the performance of the algorithm gets close to Cramer-Rao bound under the condition that the signal to noise ratio gets close to the bound of demodulation, and verify the reliability to engineering practice.

amplitude-phase modulated (APM) signal; blind carrier synchronization; burst signal demodulation

2016-01-07;

2016-02-17;网络优先出版日期:2016-09-30。

国家自然科学基金(61072046);河南省基础与前沿基金(1123004100322)资助课题

TN 911.6

A

10.3969/j.issn.1001-506X.2016.12.26

邱钊洋(1991-),男,硕士研究生,主要研究方向为通信信号分析与处理、软件无线电。

E-mail:qiuzhaoyang2010100@163.com

黄 焱(1964-),男,教授,硕士研究生导师,主要研究方向为通信信号分析与处理。

E-mail:stephen_young@163.com

欧阳喜(1973-),男,副教授,博士,硕士研究生导师,主要研究方向为软件无线电。

E-mail:oyxwlm@163.com

网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160930.1243.020.html