单脉冲最省能量拦截轨道迭代算法

2016-12-24孟少飞刘新学

系统工程与电子技术 2016年12期

关键词：单圈拦截器变轨

孟少飞, 刘新学, 傅丹, 杨其

(1.火箭军工程大学初级指挥学院, 陕西西安 710025; 2. 中国航天科技集团公司第一研究院, 北京 100071)

单脉冲最省能量拦截轨道迭代算法

孟少飞1, 刘新学1, 傅丹2, 杨其1

(1.火箭军工程大学初级指挥学院, 陕西西安 710025; 2. 中国航天科技集团公司第一研究院, 北京 100071)

最优拦截轨道解算是航天器在轨拦截问题中的重要内容,是天基武器研发中需要解决的核心技术难题之一。由于轨道解算方程和拦截方程是隐式非线性方程,因此很难用解析的方法进行分析和计算。针对非固定拦截点条件下的拦截轨道优化问题,分析讨论了拦截轨道参数和拦截器变轨点特征速度随拦截时间和拦截真近点角的变化规律。在此基础上,研究了由拦截轨道的真近点角反向求解拦截初始参数问题,并设计了能量最省拦截轨道的快速迭代算法。最后通过仿真,验证了算法的可行性和快速性。

空间拦截; 特征速度; 快速迭代

0 引言

随着现代空间技术的发展,夺取制天权并保持空间优势已经成为世界各国的重要军事发展战略。同时,空间对抗技术与手段随着空间技术的发展进步而变得越来越复杂与多样,其约束性越来越多,偶然性也越来越大。空间拦截作为空间对抗的重要内容,其首要的约束条件即是拦截器所携带的能量的约束[1-2],除此之外还有其他战术条件上的约束,包括拦截时间[3-4]、拦截窗口[5-6]、拦截位置[7]等约束条件。随着多脉冲变轨技术和多圈拦截交会技术的发展,虽然多脉冲拦截和多圈拦截所需的能量往往小于单脉冲单圈拦截所需的能量,但是考虑到天基武器的特殊作战需求以及“发出后不管”的高效作战模式,单脉冲拦截相比多脉冲拦截能减小作战所需的后续轨道保障成本和可靠性;而相比于多圈拦截模式,单圈拦截能较少拦截轨道和目标轨道的交叉,减小暴露作战意图和轨道被跟踪探测的风险。

由于最优拦截轨道的解算问题是一个具有多个局部最优解的非线性优化问题,如何避免算法陷入局部最优成了首先需要考虑的问题。文献[8-9]研究了起点和终点固定而飞行时间不定情况下所需能量随飞行时间的变化规律和极小能量轨道;文献[10-11]采用了全局搜索的方法实现了对单脉冲最省能量拦截轨道的计算;文献[12-17]以能量最省、拦截时间最短、脱靶量最小为综合指标,采用遗传算法等组合优化算法对单脉冲拦截轨道的优化进行了研究。而本文考虑在轨拦截中拦截起点固定而拦截终点不固定条件下的单脉冲单圈最省能量拦截问题,从转移速度增量的变化规律角度入手设计了能量最省拦截轨道的数值迭代算法,既提高了算法的快速性与可靠性,又避免了陷入局部最优的问题。

1 非固定终端拦截特征速度变化规律

转移轨道示意图如图1所示,航天器先后通过固定端点P1、P2时的位置矢量为r1、r2,速度矢量为v1、v2,c为连接P1、P2的弦长,当其轨道为椭圆时,所需要的时间Δt和转移轨道半长轴a之间的关系[18-19]为

(1)

这就是Lagrange转移时间方程,其中α、β为拉格朗日参数,且有

(2)

(3)

(4)

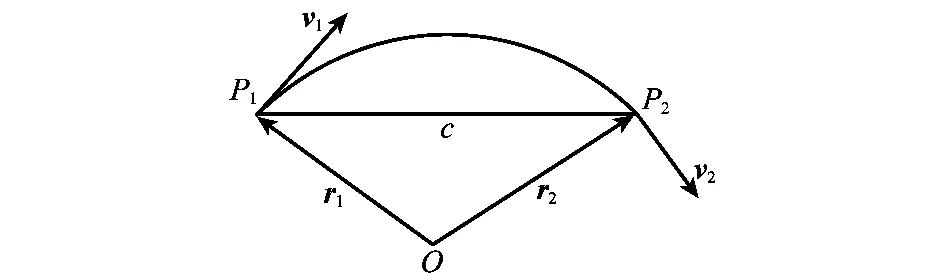
图1 转移轨道示意图Fig.1 Transfer orbit sketch map

1.1 特征速度关于轨道半长轴的导数

设拦截器变轨点速度增量的大小为Δv,则有

(5)

式中,v+和v-为拦截器变轨前和变轨后的速度；φ为它们的夹角。可以看出,当变轨时刻和拦截时刻都不确定时,Δv为变量v+、v-和φ的函数;而当变轨时刻确定而拦截时刻不确定时,Δv仅为变量v+和φ的函数。

设a为变轨后拦截轨道的半长轴,将式(5)两边分别对a求导[20]有

(6)

其中

(7)

(8)

由椭圆轨道的速度公式得

(9)

对式(1)～式(9)两边求导可得

(10)

此时,式(6)右边4个因式中,还有dφ/da没有解决。为解决这一因式,需要确定φ和变轨后的方向角γ+的关系,如图2所示。

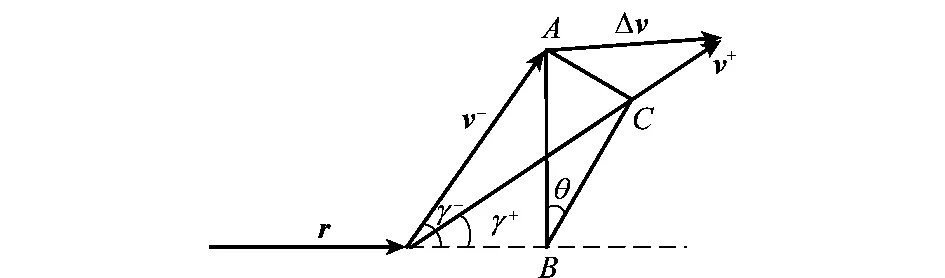
图2 变轨前后速度变化示意图Fig.2 Change of velocity before and after orbital transfer

图中,γ-和γ+为变轨前后的飞行方向角,且有γ-<90°,γ+>90°。过A点作AB垂直于变轨点位置矢量r于B点,过B点在拦截轨道平面内作垂直v-的直线交v+于C点。通过三角函数关系可以得到

cosφ=cosγ+cosγ-+sinγ+sinγ-cosθ

(11)

将式(11)两边对a求导可得

(12)

式(11)和式(12)中的γ+、γ-和θ可以由以式(13)求得:

(13)

(14)

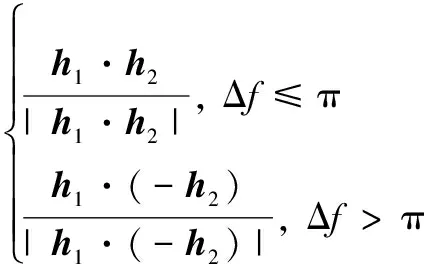
(15)

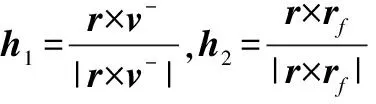
(16)

又由式(13)可得

(17)

(18)

同时,对式(1)求导可得

(19)

(20)

(21)

至此,可以求出特征速度Δv对拦截轨道半长轴a的导数。

1.2 特征速度的变化规律

当拦截时间较长时,可以分为多圈拦截和单圈拦截,多圈拦截是指拦截器变轨后经过多个转移轨道的轨道周期后拦截指定目标,单圈拦截则是指拦截器变轨后在一个轨道周期内拦截指定目标。显然,多圈拦截的特征速度往往小于单圈拦截的特征速度。但是多圈拦截的缺点是拦截器多次经过拦截点,这样则容易暴露其拦截意图,且容易被目标航天器跟踪与规避。当拦截的时间控制在合适的范围内时,采用单圈拦截需要的最小速度增量和多圈拦截最小速度增量接近,且战术效果优于多圈拦截。仅考虑单圈拦截的情况下,拦截时间t和变轨特征速度Δv随拦截轨道半长轴a的变化规律如图3所示。

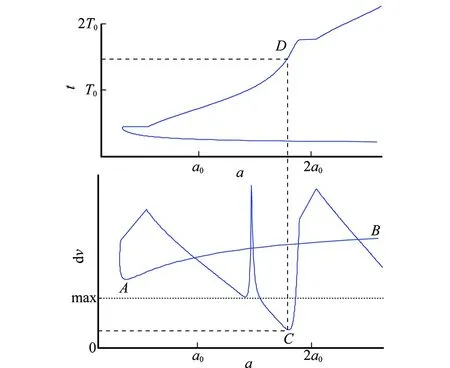
图3 t和Δv随a的变化规律Fig.3 Rule of t and Δv with the change of a

由图3可以看出,当拦截时间较小时,所需要的速度增量较大,如图中AB段曲线所示。由A点以后的一个时间周期内,拦截特征速度有两个极小值,而符合条件的全局极小值只有一个C点,它所对应的拦截时间为D。可以看出,拦截轨道优化问题是具有多个局部最优解的非线性优化问题,在不同的区间内存在不同的局部最优解,且全局最优解是唯一存在的,而求解最优拦截轨道问题的本质则是求解全局最优解。

但在图3中,拦截轨道特征速度在各区间的变化是非单调的,且拦截轨道半长轴和拦截轨道特征速度之间并非单映射的关系,无法用数值迭代的方法求解局部最优拦截轨道。为了方便问题的解决,考虑用转移轨道的真近点角Δθ取代转移轨道半长轴a,讨论特征速度Δv的变化规律。

(22)

(23)

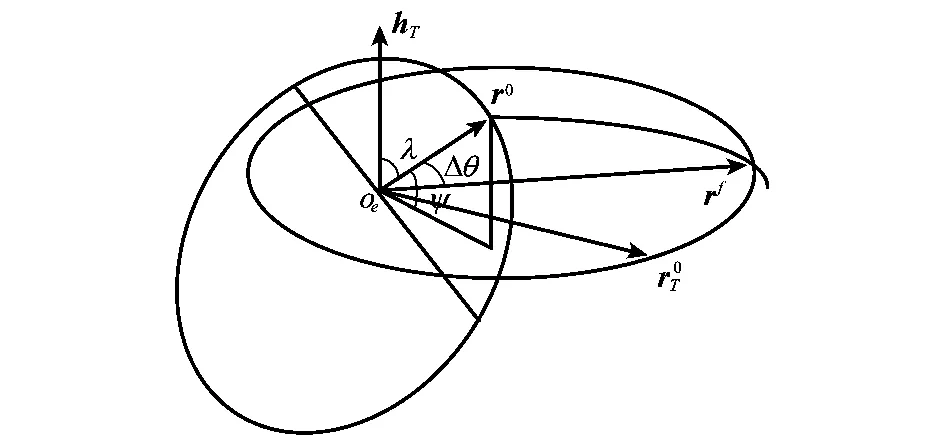
图4 Δθ的变化范围Fig.4 Variation range of Δθ

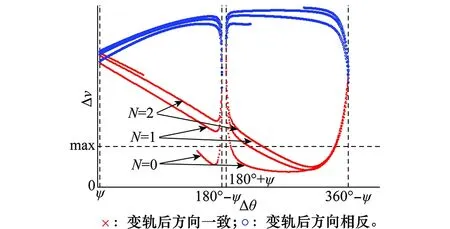
图5 Δv随Δθ的变化规律Fig.5 Rule of Δv with the change of Δθ

可以看出:虽然Δv的变化规律与变轨时刻的具体条件有关,但由于目标航天器的周期性运动,导致Δv在不同的周期内,具有相似的变化规律;在目标的一个运动周期内,当拦截轨道与原轨道方向一致时,Δv存在唯一最小值Δvmin,且以Δvmin为分界,其两侧的变化分别都是单调的。

2 最省能量拦截轨道快速迭代算法

2.1 迭代算法的总体思想和基本模型

(Δθ0,Δv0),…,(Δθn-1,Δvn-1),(Δθn,Δvn)

则有

(24)

设该区间内的局部最优解为F,值为(Δθf,Δvf),则有

(25)

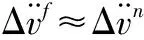
(26)

当计算精度满足要求时,迭代停止:

|Δvn-Δvn-1|≤δ

(27)

由式(26)可以看出,迭代条件是至少需要已知前面两个点,因此迭代初始可以手动选择一个点进行计算,作为迭代初始条件。当获得多个时间周期内的多个局部最优解后(当N≠0时,取ΔtN=Δt0+TT·N即可),通过比较每个局部最优解得能量成本和时间成本,结合规定的拦截时间窗口,从中选择最合适的解作为全局最优解。一般计算2～3个周期即可找到全局最优解。

迭代算法的流程图如图6所示。

图6 迭代算法流程图Fig.6 Iteration algorithm flow chart

2.2 最省能量拦截轨道参数解算

当迭代算法确定后,还需要解决如何由拦截轨道的真近点角Δθ计算拦截器变轨所需要的特征速度Δv。设m为拦截轨道的方向,1表示顺行,-1表示逆行;设变量Δθ*、m*为拦截轨道所对应的最便捷路径参数,并与原始参数Δθ*、m*的关系为

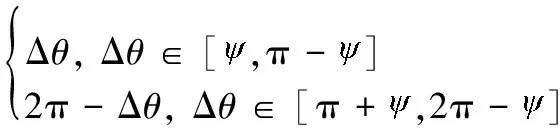
(28)

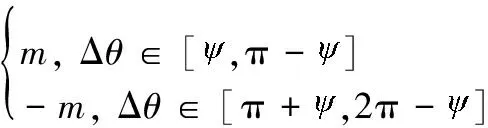
(29)

(30)

为了便于求解方程(30),设

(31)

又设

(32)

则方程(30)的解可以表示为

(33)

设方程(30)的两个解分别为n1、n2,则需要排除掉一个不符合实际情况的解。具体方法是计算

(34)

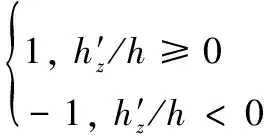
(35)

若m*=m′,则对应的ni为所求解。若m*≠m′,则对应的ni需要筛除。当n确定后,计算

(36)

(37)

设ΔθT为目标飞行过的真近点角度,则有

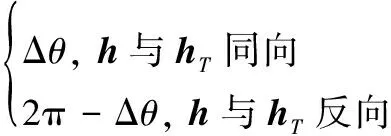
(38)

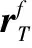
3 仿真算例

设初始时刻拦截器和目标的轨道根数如表1所示。拦截器在t=0时刻开始机动变轨,拦截时间约束为Δt≤4 h。通过仿真,可以得到变轨点速度增量随拦截器转移真近点角的变化关系如图7所示,迭代所得的局部最优解如表2中所示。

表1 目标和拦截器初始轨道根数

图7 仿真算例中Δv随Δθ的变化规律Fig.7 The rule of Δv with the change of Δθ in the simulation example

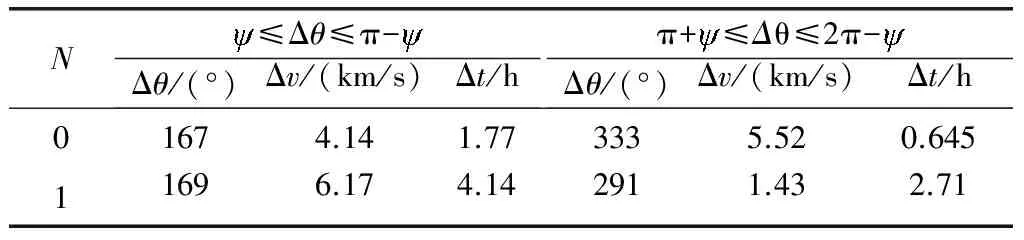
N≤Δθ≤π-Δθ/(°)Δv/(km/s)Δt/hπ+≤Δθ≤2π-Δθ/(°)Δv/(km/s)Δt/h01674．141．773335．520．64511696．174．142911．432．71

通过对表2中各个周期中不同区间段的局部最优解比较可得,当拦截轨道真近点角Δθ为291°时,拦截器变轨所需要的特征速度Δv达到全局最小值1.43 km/s,与之对应的拦截时间Δt为2.7 h,所需的变轨特征速度矢量为

Δvmin=

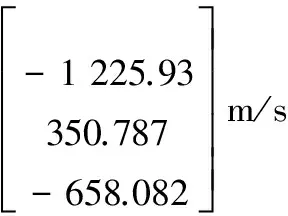
对比图7中的特征速度变化曲线可以看出,迭代算法求得的最优解为全局最优解,这验证了迭代算法的正确性。在此条件下的最优拦截轨道如图8所示。

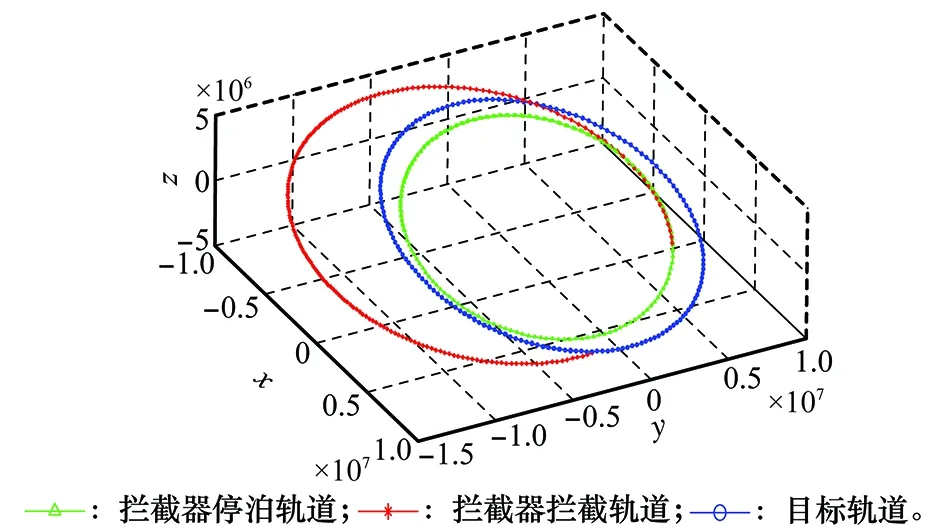
图8 拦截轨道三维仿真图Fig.8 The three-dimensional emulational interception orbit

迭代计算过程中的迭代次数和所用时间如表3所示,可以看出各区间迭代的平均次数在30次左右,这对计算机来说属于较小的计算量,所用的最大迭代时间为0.031 s,很好地满足了天基武器快速性反应的要求,同时也说明此迭代方法的快速性。

表3 不同区间最省能量轨道迭代次数与时间

Table 3 The complexity and time of iteration for the optimal interception orbit

N≤Δθ≤π-迭代次数时间/sπ+≤Δθ≤2π-迭代次数时间/s0300．031310．0311320．016300．025

4 结论

文章探讨了在一般天基拦截问题中,拦截终点不固定条件下的最省能量拦截轨道。首先仿真研究了变轨点速度增量随拦截器飞过的真近点角的变化曲线并探讨了其共性特点;其次在此基础上研究设计了最省能量拦截轨道的分段迭代方法,并进行了仿真验证,证明了该方法的有效性。此算法实现起来较为简单,迭代速度也较快,能满足星载计算机的实时计算能力要求。同时,通过对起点固定而终点不固定的最省能量拦截问题的研究,能为起点和终点都不固定的无约束最省能量在轨拦截和交会问题提供一定的借鉴意义和理论支撑。

[1] Henzeh L, Donghoom K, James T. Solution for nonlinear three-dimensional intercept problem with minimum energy[J].MathematicalProblemsinEngineering, 2013: 435725.

[2] Chen X G, Wu Z L, Gao Y. Design and optimization of space-based interception orbit based on energy[J].ComputerSimulation,2012,29(5):59-63.(陈小刚,吴志林,高宇.基于能量的天基拦截轨道设计与优化[J].计算机仿真,2012,29(5):59-63.)

[3] Bai H B, Feng S X, Zhu L P. Simulation of fixed-time orbit interception in space warfare[J].AerospaceControl, 2006, 24(4): 62-66.

[4] Gao H, Zhu Z X, Liu J. An effective minimum-time orbital transfer design under continuous thrust[J].JournalofNorthwesternPolytechnicalUniversity,2012, 30(2): 187-191.(高怀,朱战霞,刘剑. 基于遗传算法的连续推力最短时间转移轨道设计[J]. 西北工业大学学报, 2012, 30(2): 187-191.)

[5] Leeghim H. Spacecraft intercept using minimum control energy and wait time[J].CelestialMechanicsandDynamicalAstronomy, 2013, 115(1): 1-19.

[6] Liu H, Lei T, Li S L, et al. Optimal design for impulsive orbit maneuver based on parameters optimization thinking[J].AerospaceShanghai, 2010(1)：20-25.(刘恒,雷涛,李顺利,等.基于参数优化的脉冲轨道设计[J].上海航天,2010(1)：20-25.)

[7] Wei P T, Lei G, Guo H N, et al. Orbit interception at virtual crossing point based on Lambert transfer[J].FlightDynamics, 2012, 30(6):556-559.(魏鹏涛,雷刚,郭洪娜,等.基于Lambert转移的虚交点轨道拦截优化[J].飞行力学,2012,30(6):556-559.)

[8] Lu T, Zhu J. A genetic algorithm for finding a path subject to two constraints[J].AppliedSoftComputing, 2013, 13(2):891-898.

[9] Ulybyshev Y. Continuous thrust orbit transfer optimization using large-scale linear programming[J].JournalofGuidanceControlandDynamics, 2007, 30(2): 427-436.

[10] Chao T, Wang S Y, Wang Z C, et al. Near space vehicle trajectory optimization approach based on hybrid SVM and GA algorithm[J].JournalofAstronautics, 2012, 33(2): 183-188.(晁涛, 王松艳,王子才,等. 基于组合优化算法的临近空间飞行器轨迹优化[J]. 宇航学报,2012,33(2): 183-188.)

[11] Yan Y H, Guo D C. Indirect optimization for finite-thrust orbital interception problem[J].AppliedMechanicsandMaterials, 2013, 313/314: 1051-1054.

[12] Zheng Q, Sha J X, Shu H, et al. A variant constrained genetic algorithm for solving conditional nonlinear optimal perturbations[J].AdvancesinAtmosphericScience,2014,31(1):219-229.

[13] Leung C S, Lam P M, Tsang P W M. A graphics processing unit accelerated genetic algorithm for affine invariant matching for broken contours[J].JournalofSignalProcessingSystemsforSignalImageandVideoTechndogy,2012,65(2):105-111.

[14] Li X S, Wang M J, Zhao X Y, et al. Finite thrust orbit interception optimization using hybrid genetic algorithm[J].ComputerSimulation, 2010, 27(12) : 20-23.(李新三,王明建,赵旭阳,等.采用混合遗传算法的有限推力拦截轨道优化[J].计算机仿真,2010,27(12): 20-23.)

[15] Tang Y H, Chen S L, Xu M, et al. A genetic algorithm (GA) method of orbit interception with finite thrust[J].JournalofNorthwesternPolytechnicalUniversity,2005,23(5):671-674.(汤一华,陈士橹,徐敏,等.基于遗传算法的有限推力轨道拦截优化研究[J].西北工业大学学报,2005,23(5):671-674.)

[16] Qi Y H, Cao X B. Design of optimal multiple-impulsive rendezvous trajectory using genetic algorithm[J].JournalofHarbinInstituteofTechnology, 2008, 40(9): 1345-1349.(齐映红,曹喜滨.基于遗传算法的最优多脉冲交会轨道设计[J].哈尔滨工业大学学报,2008,40(9):1345-1349.)

[17] Li Y, Li X J, Zhang D L, et al. Application of hybrid genetic algorithm in optimal Lambert orbital transfer design[J].FlightDynamics, 2013, 31(3): 269-272.(李勇,李小将,张东来,等. 混合遗传算法在最优Lambert轨道转移设计中的应用[J]. 飞行力学,2013,31(3):269-272.)

[18] Zhao R A.Spaceweaponorbitdesign[M]. Beijing:China Aerospace Press, 2008.(赵瑞安.空间武器轨道设计[M].北京:中国宇航出版社, 2008.)

[19] Xu P D, Huang S Y, Li Z M. A new method for determining intercepting orbit of space kinetic weapon[J].ComputerSimulation, 2009, 26(6):54-58.(徐培德,黄思勇,李志猛.天基动能武器拦截轨道的确定方法研究[J].计算机仿真,2009,26(6):54-58.)

[20] Zhang P Y. Optimal trajectory design for space interception[D]. Harbin: Harbin Institute of Technology, 2009.(张鹏宇.空间拦截最优轨道设计[D].哈尔滨:哈尔滨工业大学,2009.)

Iterative algorithm for minimum-energy interception orbit with single pulse

MENG Shao-fei1, LIU Xin-xue1, FU Dan2, YANG Qi1

(1.PrimaryCommandCollege,TheRocketForceUniversityofEngineering,Xi’an710025,China; 2.TheFirstInstituteofChinaAerospaceScienceandTechnologyCorporation,Beijing100071,Chian)

Optimal interception orbit calculation is important content of spacecraft on-orbit interception question, and is one of the core technical problems of space-based weapons development. It’s difficult to analytically analyze and calculate because of the nonlinearity and implicitness of orbit calculation equations and interception equations. Aiming at interception trajectory optimization problem with no-constant interception point, the law of interception trajectory parameter and characteristic velocity in transfer point changing with interception time and interception true anomaly is summed up. On this basis, the calculation of the initial interception parameters from interception orbit true anomaly has been researched and rapid iterative algorithm for minimum-energy interception trajectory has been designed. Finally, practicability and rapidity of the algorithm is verified by simulation.

space interception; characteristic velocity; rapid iterative

2015-07-16;

2016-10-20;网络优先出版日期:2016-10-27。

V 448

10.3969/j.issn.1001-506X.2016.12.21

孟少飞(1989-),男,博士研究生,主要研究方向为飞行动力学与制导。

E-mail:627786952@qq.com

刘新学(1964-),男,教授,博士,主要研究方向为飞行动力学与制导。

E-mail:bobxaliang@yahoo.com.cn

傅丹(1979-),女,博士,主要研究方向为飞行器总体设计。

E-mail:1126043246@qq.com

杨其(1983-),男,博士研究生,主要研究方向为惯性制导与控制。