基于证据特征的区间证据合成方法研究

孙伟超, 许爱强, 李文海

(1. 海军航空工程学院研究生管理大队, 山东 烟台 264001;2. 海军航空工程学院飞行器检测与应用研究所, 山东 烟台 264001)



基于证据特征的区间证据合成方法研究

孙伟超1, 许爱强2, 李文海2

(1. 海军航空工程学院研究生管理大队, 山东 烟台 264001;2. 海军航空工程学院飞行器检测与应用研究所, 山东 烟台 264001)

基于区间值的证据合成理论可以有效地描述和处理不确定性问题,针对目前区间证据合成方法存在融合失效的问题,分析了其产生的原因并提出新的区间证据组合方法。对证据源本身的特征进行提取,依此对证据进行修改,并提出两种优化方法用于区间信度结构下的证据合成。数值实验结果表明,提出的方法收敛性、鲁棒性较好,在面对冲突区间证据融合时得到了合理的结果。

区间证据理论; 特征提取; 证据组合

0 引 言

证据理论是关于证据推理的数学理论,其对不确定性问题的推理方法符合人们的思维习惯,是主观Bayes理论的一种推广,能在不需要先验概率的情况下,表示不精确性和不确定性,处理不完整数据[1]。目前,证据理论因其坚实的数学基础,简单的推理形式,已广泛应用于人工智能、信息融合、数据挖掘等领域。

经典D-S证据理论中需要基本概率赋值函数取值为介于0和1之间的精确单点值。但是在大部分情况下,由专家给出的基本概率赋值并不是精确的,而是一个区间值。在决策分析过程中,将这些区间值合成一个精确的点估计是困难的,也是不必要的。文献[2]认为基于区间值的概率可以更简洁的表示模糊性和不完全性,因此,基于区间值的证据合成理论研究可以有效拓展经典D-S证据理论的应用范围。

由于经典D-S理论中单点值概率赋值函数不易获取,国内外的一些学者展开了对区间值证据组合问题的研究,并取得了一些进展。文献[3]最早研究了区间证据合成,定义了广义和与广义乘积运算,并基于此得出区间证据合成规则,但该方法缺少对正规化的考虑,导致其合成结果易出现错误。文献[4]也对区间证据合成的问题做过研究,但其计算区间证据合成时用到了区间算数规则,可能会出现上边界概率小于下边界概率的情况,导致错误。文献[5]的研究在TBM框架下进行,同时考虑正规化合成与非正规化合成,但由于区间证据合成与正规化过程分离,优化过程批次独立,导致得出的结果为次优的。为了解决这个问题,文献[6-7]对Denoeux方法进行了研究,并对该方法进行了改进,提出了一种区间值概率赋值函数合成与正规化的最优化方法。它同时考虑合成与正规化运算,得到最优的焦元基本概率赋值区间。

近年来,对区间证据融合问题的研究主要集中在两个方面,对融合规则的修改以及对区间证据理论在应用上的拓展。在区间证据融合过程中,存在结果区间过于宽泛以及冲突证据合成失效的问题[8]。针对结果区间过大问题,文献[9]提出焦元的最大置信区间的概念,并以此对区间信度结构进行处理;在冲突证据合成时,文献[10]指出因Dempster方法缺少正规化过程,会存在合成失效的情况。文献[11]认为应根据冲突程度决定是否使用Dempster方法,因此将精确信度结构情况下的一致性测量方法拓展到区间信度结构上,对冲突程度进行衡量。而更多的学者选择对证据进行修正,文献[12]提出了多种证据理论框架下的相异度度量方法;文献[13]通过获取区间证据置信度,对原始证据进行加权平均得到新的证据;文献[14]构建了证据间pignistic概率距离的最优化模型,并以此对证据进行修正;文献[15-16]则给出证据相关情况下的区间信度融合时各证据权重的计算方法。在区间证据融合的应用中,针对不同的应用场合,学者们也进行了相应的改进。文献[17]利用区间信度结构提出一种不确定数据的参数估计方法;文献[18]在多传感器目标识别中,将传感器的可靠性作为每一条证据的权重,传感器得到的,不确定信息转换为区间值,用所提的新算法进行组合;文献[19]在决策系统中,在区间信度结构下构建了新的决策模型,并将多种聚合算子拓展,并提出一种将区间权重用于这些聚合算子的方法;文献[20]提出了区间信度结构更新规则,并将其用于故障诊断上。

由于区间值的证据合成理论可以有效地描述和处理不确定性问题,有着广泛的应用需求,因此有必要深入研究区间值证据合成方法。本文拟对之前的方法进行分析,并在此基础上,研究如何对区间冲突证据进行修改,提出一种适用范围更广泛的区间证据合成方法,并通过算例对该方法进行验证。

1 区间证据组合问题分析

设Θ为识别框架,基本概率赋值函数m是一个从集合2Θ到[0,1]的映射,A表示识别框架Θ的任一子集,记作A⊂Θ,且满足:① m(∅)=0, ② ∑A⊂Θm(A)=1。m表示证据对A的信任程度。

有时,对于同样的证据,由于数据来源的不同,会得到多个不同的基本概率赋值函数,因此,Dempster提出了一种合成方法。它假设证据源独立,并采用正交运算将其合成:

m=m1⊕m2⊕…⊕mn

式中,⊕表示合成算子。当有n个同一识别框架Θ上的基本概率赋值函数时,Dempster合成规则为

m(C)=

式中,Ai是焦元;m(A)是合成后的基本概率赋值函数。分子∑∩Ai=A∏1≤i≤nmi(Ai)反映了各个证据间的冲突程度,分母1-∑∩Ai=∅∏1≤i≤nmi(Ai)为正规化因子。

定义 1 设Θ为识别框架,Ai(i=1,2,…,n)是Θ上的焦元,区间值[ai,bi]满足0≤ai≤bi≤1,则Θ上的区间基本概率赋值函数m(Ai)有效,需满足:

(1)ai≤m(Ai)≤bi

(3)m(A)=0,∀A∉{A1,A1,…,An}

，

i=1,2,…,n

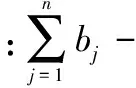
式中,(m1⊕m2⊕…⊕mn)-(C)和(m1⊕m2⊕…⊕mn)+(C)分别表示证据合成后的区间值上下限,由下面的优化模型确定:

min/max[m1⊕m2⊕…⊕mn](C)=

i=1,2,…,n;j=1,2,…,n

之前的区间证据合成方法对模型的分子和分母分别进行优化,这样会割裂其间的联系,而上述合成该方法同时考虑了区间证据合成过程与正规化过程,通过求解优化问题得到合成焦元的概率赋值区间。但该方法由于来源于Dempster组合规则。而其在处理高冲突证据时,由于归一化因子的存在,经常会得出违背常理的结果,甚至完全失效。由此推知,当该方法用于区间冲突证据组合时,也会出现方法失效的情况,类似于于Dempster组合中的全冲突悖论与0信任悖论等。下面对这种方法失效的情况进行证明。

min/max[m1⊕m2⊕…⊕mn](A)=

i=1,2,…,n;j=1,2,…,n

证毕

2 改进的区间证据合成方法

本文同时对区间证据的证据源和组合规则进行修改,对Yager公式进行推广,并把冲突的信息按照可信度重新进行分配,给出更有效的合成方法。

2.1 证据特征提取

为了衡量个证据间相似度,引入证据距离[21]概念。识别框架Θ下,有M个证据源S1,S2,…,SM,每个证据源Si可以看成一个维数为2N的行向量,其各分量为Θ的幂集2Θ中各元素对应的mi的概率分配值。则两个证据源Si,Sj之间的距离可以由下式计算:

在给出证据间距离后,就可以衡量两个证据的相似程度,其与证据距离呈反方向变化。证据的相似度定义为:sim(Si,Sj)=1-d(Si,Sj)。

从相似度的定义可以看出,两个证据的相似度反映了它们相互支持的程度。一个证据与其他证据的相似度越高,反映了其被其他所有证据支持的程度越大。由此,证据Si被其他证据支持的程度定义为Si的支持度:

本文认为,如果一个证据被其他证据支持程度越大,则该条证据的可信度越高,因此利用证据间的支持度来定义单个证据的可信度,证据Si的可信度为

当有多个证据源时,当一个证据源拥有的相似度较大的证据越多,该证据源的总体可信度越大。因此,借助证据间相似度构造证据源的可信度超球体和证据完全一致这一理想状况下的可信度超球体,据此定义证据源整体相似半径和证据完全一致时的相似半径分别为

证据源的总体可信度可表示为:E=r/R,其表示了该证据源从整体上对理想证据源的接近程度。本文以此作为决定冲突信息中需要重新划分的冲突量。若E=0,冲突信息完全赋予未知项;若E=1,则冲突信息全部在各证据间重新分配。

为了衡量各证据之间的相似度,首先提出相似度度量函数的概念。

定义 4 考虑任意映射在幂集2Θ空间上的区间信度赋值函数:m1(·),m2(·)和m3(·),Ai(i=1,2,…,g)为辨识框架Θ上的焦元,如果满足以下4个条件,则存在一个映射SM:2Θ×2Θ→[0,1]称为相似度度量函数,基本条件如下:

(1) 对称性:对于∀m1(·),m2(·)∈2θ,有SM(m1,m2)=SM(m2,m1);

(2) 一致性:对于∀m1(·),m2(·)∈2θ,且m1(Ai)=m2(Ai),Ai∈{X1,X2,…,Xg},有SM(m1,m2)=1;

(3) 非负性:对于∀m1(·),m2(·)∈2θ,有SM(m1,m2)∈[0,1];

(4) 单调性:如果SM(m1,m2)>SM(m1,m3),则m2(·)比m3(·)与m1(·)更为相似。

SM(m1,m2)被称为m1(·)与m2(·)之间的相似度度量函数。

定理 1 在幂集2Θ空间上对任意的区间信度赋值函数m1(·),如果给定一足够大的实数ε<1,则至少存在一个区间信度赋值函数m2(·),使得SM(m1,m2)>ε。

证明 使用反证法对定理进行证明。假设不存在m2(·)使得SM(m1,m2)>ε。如果m2(·)=m1(·),可知SM(m1,m2)=1,由于ε<1,所以SM(m1,m2)>ε,这与假设矛盾。又因为相似度度量SM(m1,m2)为连续的,则满足SM(m1,m2)>ε的m2(·)不唯一。

证毕

定理 2 若给定的正实数ε<1越大,则m1(·)与m2(·)之间距离越小,相似度越大。

证明 根据定理1可知,对于∀m1(·),∃m2(·)使得对∀ε<1有SM(m1,m2)>ε,随着ε的增大,则m1(·)与m2(·)之间的相似度SM(m1,m2)逐渐增大,当SM(m1,m2)=1时,m1(·)与m2(·)完全相同。

证毕

通过以上定理可知,相似度度量函数可以很好的对两证据间的相似程度进行度量,下面依托于Jousselme[21]距离给出一种相似度度量函数:

定义 5 设Θ={θ0,θ1,…θn}为辨识框架,Xi(i=1,2,…,g)为辨识框架Θ上的焦元,两证据E1,E2的区间信度赋值函数分别为m1(·),m2(·),则m1(·)与m2(·)间的相似度度量函数定义如下:

下面证明SMJ(m1,m2)是相似度度量函数。

所以,SMJ(m1,m2)=SMJ(m2,m1),SMJ(m1,m2)满足交换律。

(3) 首先证明SMJ(m1,m2)≤1。由于

故

SMJ(m1,m2)=

由于‖m1‖2≤1,‖m2‖2≤1,故当且仅当‖m1‖2=1,‖m2‖2=1,〈m1,m2〉=0时,‖m1‖2+‖m2‖2-2〈m1,m2〉=2,SMJ(m1,m2)=0。

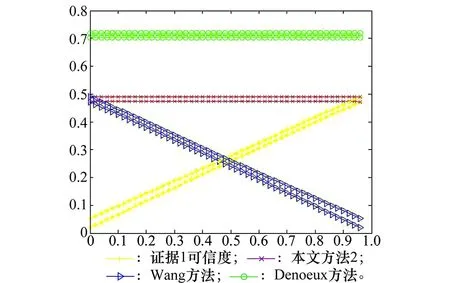
(4) 令SMJ(m1,m3)=ε<1,根据定理1,至少存在一个区间信度赋值m2(·)使得SMJ(m1,m2)>ε,此时SMJ(m1,m3)

证毕

两个证据的相似度反映了它们相互支持的程度。一个证据与其他证据的相似度越高,反映了其被其他所有证据支持的程度越大。由此,借助相似度度量函数SMJ(·,·),将证据Ei被证据群S中其他证据支持的程度定义为证据Ei的支持度:sp(Ei)=∑j≠iSMJ(Ei,Ej);如果一个证据被其他证据支持程度越大,则该条证据的可信度越高,因此利用证据间的支持度来定义单个证据的可信度,证据Ei的可信度为:crdei=sp(Ei)/∑isp(Ei)。

当有多个证据源时,当一个证据源Sl拥有的相似度较大的证据越多,该证据源的总体可信度越大。

为了对证据源Sl可信度进行度量,定义标准证据源Sstd,其中每一条证据Ei都相同。Sstd的总体可信度在所有证据源中最大。

采用证据源Sl与标准证据源Sstd的相似程度对证据源Sl的可信度进行表示。定义证据源Sl的可信度为csl=SM(Sl,Sstd)。

下面定义对度量函数SM(Sl,Sstd)进行定义。

SM(Sl,Sstd)=

SM(Sl,Sstd)=SMstd(Sl)=

性质 1Θ={θ0,θ1,…,θn}为辨识框架,Sstd为标准证据源。对于框架上的任意证据源Sl,满足:SMstd(Sl)∈[0,1]

证毕

性质 2SMstd(Sl)=1,当且仅当Sl为标准证据源Sstd。

证毕

定义 3 当证据群Sl内证据相似度越大,则可信度越高。

SMstd(Sl)/SMstd(Sk)=

可得,SMstd(Sl)>SMstd(Sk)。

证毕

由以上性质可知,证据源的可信度可以有效衡量出出该证据源对于理想状况的接近程度。故本文以证据源Sl的可信度csl作为决定冲突信息中需要重新划分的冲突量。若csl=0,表明此时证据源Sl完全不可信,冲突信息完全赋予未知项;若csl=1,则冲突信息全部在各证据间重新分配。

2.2 区间证据合成优化模型

通过上述分析,为了有效地解决多个区间证据合成问题,本文提出两种区间证据最优化合成方法。

min/max[m1⊕m2⊕…⊕mn](A)=

i=1,2,…,n;j=1,2,…,n

如果基于冲突信息量部分全部可以分配的思想,将全部冲突信息按照单个证据可信度给出的比例在各个证据间进行分配则(m1⊕m2⊕…⊕mn)-(A)和(m1⊕m2⊕…⊕mn)+(A)由下面的优化模型给出:

min/max[m1⊕m2⊕…⊕mn](A)=

i=1,2,…,n;j=1,2,…,n

3 数值实验

在本节中,将通过算例对本文所提两种方法的性质进行验证,并引入Wang方法与Denoeux方法进行对比分析。其中,通过例1对方法的有效性以及收敛性进行验证,通过例2验证方法在冲突证据融合方面的表现,例3对方法的鲁棒性进行验证,例4则对比了各方法随合成证据区间的增大,得到结果区间的变化趋势。例5,例6则给出了方法在信息融合领域中区间证据合成方向上的具体应用实例。

例 1 在Shafer模型下,已知辨识框架为Θ={A,B},3条证据的区间基本信度赋值为

E1:m1(A)=[0.00,0.04],m1(B)=[0.96,1.00],m1(A∪B)=[0.02,0.04]

E2:m2(A)=[0.96,1.00]-ε,m2(B)=[0.00,0.04]+ε,m2(A∪B)=[0.02,0.04]

E3:m3(A)=[0.96,1.00],m2(B)=[0.00,0.04],m2(A∪B)=[0.02,0.04]

在m2中,令ε=0,之后以0.02间隔步进至ε=0.96。在此过程中,证据E1由与E2相同,逐渐变为E3相同,随ε变化,焦元A,B,A∪B合成后的区间信度赋值变化趋势在图1～图3中给出。

图1 例1中m(A)随ε的变化趋势Fig.1 Variation trend of m(A) with ε in ex.1

图2 例1中m(B)随ε的变化趋势Fig.2 Variation trend of m(B) with ε in ex.1

图3 例1中m(A∪B)随ε的变化趋势Fig.3 Variation trend of m(A∪B) with ε in ex.1

从图中可以看出,随ε的增大,各方法合成后的焦元A的信度赋值呈减小的趋势,焦元B的信度赋值逐渐增大,而由于在3个证据中,由于焦元A∪B为固定值,与ε无关,故合成后的信度赋值没有变化。在焦元A,B上,本文方法得到的结果区间明显小于Wang方法与Denoeux方法。在焦元A∪B上,本文方法1得到结果区间较大,这是因为本例中,部分冲突证据作为被分配到A∪B上。为了更好的进行分析,将本文方法计算过程中,证据E1,E2,E3的相似度,可信度与证据源总体可信度随ε的变化趋势在图4和图5中给出。

图4 例1中证据相似度随ε的变化趋势Fig.4 Variation trend of evidence similarity with ε in ex.1

图5 例1中证据可信度随ε的变化趋势Fig.5 Variation trend of evidence credibility with ε in ex.1

在图4中,随ε的增大,证据2由与证据1完全相同变化为与证据3完全相同,相似度曲线有效地反映出这一变化,同时,由于证据1与证据3在焦元A与焦元B上显著不同,且不随ε变化,故其相似度曲线接近于0,且保持恒定。而在图5中,随着证据2由支持证据1转为支持证据3,导致证据1可信度下降,证据3可信度上升,而证据2与证据源总体可信度保持恒定。可以看出,证据可信度的度量方法具有良好的线性度。

例 2 在Shafer模型下,已知辨识框架为Θ={A,B},两证据的区间基本信度赋值为

E1:m1(A)=[0.00,0.04],m1(B)=[0.96,1.00]

E2:m2(A)=[0.96,1.00]-ε,m2(B)=[0.00,0.04]+ε

与上例相同,在m2中,令ε=0。在此过程中,两证据由完全冲突变为完全相同,以此验证本文方法在合成冲突证据方面的效果。焦元A,B合成后的区间信度赋值变化趋势在图6和图7中给出。

图6 例2中m(A)随ε的变化趋势Fig.6 Variation trend of m(A) with ε in ex.2

图7 例2中m(B)随ε的变化趋势Fig.7 Variation trend of m(B) with ε in ex.2

在图6中,随“冲突”变小,E2在焦元A上的信度赋值逐渐接近于[0.00,0.04],各方法得到的结果均收敛到0。在本文方法1中,证据E1,E2相似度低,导致证据源可信度开始时很小,使得合成结果接近于0,随ε增大,合成结果逐渐增大,后由于E2接近于[0.00,0.04],合成结果收敛到0。本文方法2由于不考虑该证据源的总体可信度,在证据E1,E2完全冲突时,给两者赋予相同权重,取到中间值为0.5的区间值,随后随ε变化合成结果趋近于0。Wang方法与Denoeux方法得到的结果相同,在“冲突”较大的情况下,得到的结果区间值过大。在完全冲突时,获得结果区间为[0,1]。在图7中,E2在焦元B上的信度赋值接近于[0.96,1.00],各方法得到的结果均收敛到1。由于证据源总体可信度属于[0,1],故本文方法1得到的结果总小于本文方法2,Wang方法与Denoeux方法同样面临强“冲突”下结果区间过大的问题。

例 3 在例1中,使证据E2的区间信度赋值发生少量变化,以此对本文方法的鲁棒性进行验证。当ε=1×10-2,ε=1×10-4,ε=1×10-6,ε=1×10-8时,各方法所得的合成结果在表1中给出。

表1 本文方法合成结果

从表1中可以看出,随着证据区间变化幅度的减小,所得到的各焦元结果区间变化随之减小,并趋于稳定。本文方法对合成中的冲突进行了保留,不存在归一化的问题,因此在面对证据区间信度赋值发生少量变化时,所得到结果不受影响,具有较好的鲁棒性。

例 4 在Shafer模型下,已知辨识框架为Θ={A,B},两证据的区间基本信度赋值为

E1:m1(A)=[0.50-η,0.50+η],m1(B)=[0.20,0.80]

E2:m2(A)=[0.20,0.80],m2(B)=[0.20,0.80]

在合成过程中令η以0.01间隔从η=0步进至η=0.50。此时信度区间m1(A)由[0.50,0.50]增大至[0.00,1.00],以此对本文方法在证据区间增大时所得结果的合理性进行验证。在图8中给出焦元A合成后的区间信度赋值变化趋势。

图8 例4中m(A)随η的变化趋势Fig.8 Variation trend of m(A) with η in ex.4

从图中可以看出,随待合成信度赋值m(A)区间范围的增大,各方法所得到的结果区间呈增大趋势。当增大到一定程度后,即η≥0.3后,结果不发生变化,这是由于约束条件使得m(A)最大取值范围仅能为[0.20,0.80]。可以看出,各方法所得的结果均有效。而此时本文两种方法所得到的合成结果区间包含于Wang方法与Denoeux方法的结果区间中。

例 5 在雷达目标融合应用中,由5部雷达对同一批次目标进行识别。其中,每一部雷达分别为目标进行信度赋值,通过合成得到最终结果。对于三目标区分,计算是首先构建辨识框架Θ={A,B,C},分别代表3个目标。各雷达对3个目标的支持程度作为区间信度赋值,在表2中给出,使用本文方法1与Wang方法对证据进行合成,结果在表3中给出。

可以看出,在多部雷达中,E1，E3，E4，E5都倾向于支持目标A,而E2在很大程度上支持目标B,对A的支持度为0,与其余证据有很大冲突。

表2 例5中基本区间信度赋值

表3 例5区间合成结果

通过对表3中结果进行分析,面对高冲突证据,Wang方法始终给出m(A)=0的结果,与实际不符;同时,随着参与合成的证据源增多,概率区间呈增大趋势,合成效果变差,故此时该方法不能做出有效决策。本文方法1在证据E1与E2融合过程中,将大部分冲突信息赋予辨识框架Θ,随着证据的加入,最终得到A的概率区间为m12345(A)=[0.431,0.514],这一结果已经很接近于证据E1，E3，E4，E5对A的赋值区间,有效去除了E2的干扰。这是因为随着证据的加入,证据E1，E3，E4，E5距离较近,获得了较高的支持度,在对冲突信息进行分配的过程中占有较大权重。而且随着参与合成的证据增多,赋予Θ的未知信息逐渐减少。

例 6 在多传感器故障诊断应用中,由各传感器采集故障数据,再通过对其给出的结果进行信息融合,对系统故障状态进行判断。

假设辨识为Θ={A,B,C,D,E},分别表示5种单发故障,由于数据存在缺失的情况,4个传感器给出的各故障模式下的信度赋值为区间值,见表4。使用本文方法2与Wang方法对证据进行合成,结果在表5中给出。

表4 例6中基本区间信度赋值

表5 例6区间合成结果

从表5中可知,两种方法组合得到的结果基本一致,给出的辨识框架内各焦元区间概率赋值大小顺序基本相同。但是,由于数据中给出的m3(C)和m4(B)区间概率赋值很小,导致Wang方法给出的合成结果m123(C),m1234(C),m1234(B)显著减小,无法反映出其他证据对该焦元的影响。本文方法2通过对证据源进行适当的修改,减弱了这种影响,避免合成结果出现大幅度波动。在合成证据弱冲突的情况下,本文方法与Wang方法一致,都可以得到合理有效的融合结果。

4 结束语

针对目前在区间信度结构合成中可能存在的冲突证据融合失效及所获得的结果区间偏大的问题,本文在分析了现有区间证据融合方法的前提下,通过对证据特征进行分析,将证据源的特征应用到对证据的修改过程中,同时基于冲突信息量部分可以利用与冲突信息量全部可以利用的思想,提出了两种优化模型。数值实验表明,两种方法收敛性、鲁棒性较好,在冲突区间证据融合时都得到较为合理的结果。

[1] Zhang L.Representation,independence,andcombinationofevidenceintheDempster-Shafertheory[M]∥New York: Wiley, 1994: 51-69.

[2] Cui W, Blockley D I. Interval probability theory for evidential support[J].InternationalJournalofIntelligentSystems, 1990, 5(2): 183-192.

[3] Lee E S, Zhu Q. An interval Dempster-Shafer approach[J].Computers&MathematicswithApplications, 1992, 24(7): 89-95.

[4] Yager R R. Dempster-Shafer belief structures with interval valued focal weights[J].InternationalJournalofIntelligentSystems, 2001, 16(4): 497-512.

[6] Wang Y M, Yang J B, Xu D L, et al. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J].EuropeanJournalofOperationalResearch, 2006, 175(1): 35-66.

[7] Wang Y M, Yang J B, Xu D L, et al. On the combination and normalization of interval-valued belief structures[J].InformationSciences, 2007, 177(5): 1230-1247.

[8] Loui R P. Interval-based decisions for reasoning systems[J].MachineIntelligence&PatternRecognition, 1985, 4(3): 459-472.

[9] Su Z, Wang P, Yu X, et al. Maximal confidence intervals of the interval-valued belief structure and applications[J].InformationSciences, 2011, 181(9): 1700-1721.

[10] Yager R R. On the fusion of imprecise uncertainty measures using belief structures[J].InformationSciences, 2011, 181(15): 3199-3209.

[11] Fu C, Yang S L. Analyzing the applicability of Dempster’s rule to the combination of interval-valued belief structures[J].ExpertSystemswithApplications, 2011, 38(4): 4291-4301.

[12] Jousselme A L, Maupin P. Distances in evidence theory: comprehensive survey and generalizations[J].InternationalJournalofApproximateReasoning, 2012, 53(2): 118-145.

[13] Feng H S, Xu X B, Wen C L. A new fusion method of conflicting interval evidence based on the similarity measure of evidence[J].JournalofElectronics&InformationTechnology, 2012, 34(4): 851-857.(冯海山, 徐晓滨, 文成林. 基于证据相似性度量的冲突性区间证据融合方法[J]. 电子与信息学报, 2012, 34(4): 851-857.)

[14] Chen S Q, Wang Y M. Conflicting evidence combination of interval-valued belief structures[J].SystemsEngineeringTheory&Practice,2014, 11(1): 256-261.(陈圣群, 王应明. 区间值信念结构下冲突证据组合[J]. 系统工程理论与实践, 2014, 11(1):256-261.)

[15] Fu C, Yang S. The combination of dependence-based interval-valued evidential reasoning approach with balanced scorecard for performance assessment[J].ExpertSystemswithApplications, 2012, 39(3): 3717-3730.

[16] Fu C, Yang S. The conjunctive combination of interval-valued belief structures from dependent sources[J].InternationalJournalofApproximateReasoning, 2012, 53(5): 769-785.

[17] Deng X, Hu Y, Chan F T S, et al. Parameter estimation based on interval-valued belief structures[J].EuropeanJournalofOperationalResearch, 2015, 241(2): 579-582.

[18] Liu H J, Nie H S, Yu H Q, et al. Modified interval Dempster-Shafer theory and its application for target identification[J].AppliedMechanicsandMaterials,2012,190(4):1153-1156.

[19] Merigo J M, Casanovas M. Decision-making with uncertain aggregation operators using the Dempster-Shafer belief structure[J].InternationalJournalofInnovativeComputing,InformationandControl, 2012, 8(2): 1037-1061.

[20] Xu X, Liu P, Sun Y, et al. Fault diagnosis based on the updating strategy of interval-valued belief structures[J].ChineseJournalofElectronics, 2014, 23(4):753-760.

[21] Jousselme A L, Grenier D. A new distance between two bodies of evidence[J].InformationFusion, 2001, 2(2): 91-101.

Research on combination of interval-valued belief structures based on features of evidence

SUN Wei-chao1, XU Ai-qiang2, LI Wen-hai2

(1.GraduateManagementUnit,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China;2.AutomaticTestEquipmentLaboratory,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China)

Combination of interval-valued belief structures can describe and deal with uncertainty problems effectively. In order to solve the problems of fusion failure existed in current methods, its reasons are analyzed. The new method extracts the characteristics of evidence source and modifies the evidence according to the characteristics. The evidence is modified according to the characteristics extracted from the evidence, and two kinds of optimization models are proposed to combine the interval-valued belief structure. The experiment results show that the proposed method is convergent and robustness. And reasonable result can be obtained in the face of combination of interval-valued belief structure with confliction.

interval-valued evidence theory; features extraction; combination of evidence

2015-01-16;

2016-02-20;网络优先出版日期:2016-10-24。

总装武器装备预研基金项目(9140A27020214JB14436)资助课题

TP 182

A

10.3969/j.issn.1001-506X.2016.12.17

孙伟超(1986-),男,博士研究生,主要研究方向为智能故障诊断。

E-mail:ben_phoenix@163.com

许爱强(1963-),男,教授,博士,主要研究方向为复杂电子装备故障诊断。

E-mail:xuaq6342@yahoo.com.cn

李文海(1969-),男,教授,博士,主要研究方向为军用电子装备故障诊断。

E-mail:ythylwh@vip.163.com

网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20161024.2059.008.html