复杂环境下的UWB脉冲成形算法

孙希延, 刘 健, 纪元法

(1. 桂林电子科技大学信息与通信学院, 广西 桂林 541004;2. 广西精密导航技术与应用重点实验室, 广西 桂林 541004)



复杂环境下的UWB脉冲成形算法

孙希延1,2, 刘 健1, 纪元法1,2

(1. 桂林电子科技大学信息与通信学院, 广西 桂林 541004;2. 广西精密导航技术与应用重点实验室, 广西 桂林 541004)

针对超宽带定位系统在多用户和弱信号环境下接收端易出现码间串扰(inter symbol interference, ISI)和多用户干扰(multiuser interference, MUI)等问题,提出一种基于修正最小均方误差估计(minimum mean square error estimation, MMSE)的自适应迭代算法进行超宽带(ultra-wideband,UWB)脉冲设计。该算法选取修正Hermite多项式(modefied Hermite polynomial, MHP)作为脉冲设计基函数。通过分析MHP的时频特性对最小均方误差估计准则下组合脉冲的各阶MHP系数进行修正,在此基础上根据组合脉冲功率谱密度与美国联邦通讯委员会(federal communications commission, FCC)辐射掩蔽之间的拟合程度设计自适应算法,对组合脉冲进行自适应调整实现脉冲设计。仿真结果表明该方案获得的脉冲有较高功率利用率,同时在多用户接入和弱信号检测方面也具备很强的适用性。

修正Hermite多项式; 自适应迭代; 多用户干扰; 弱信号检测

0 引 言

超宽带通信的信号载体是时域很窄且占空比很低的脉冲。已有多种脉冲波形被提出用来设计超宽带(ultra-wideband,UWB)脉冲,如Laplace脉冲、高斯脉冲、Rayleigh脉冲、Hermite脉冲、扁长椭球波脉冲等。但在美国联邦通讯委员会(federal communications commission, FCC)规定的UWB频段3.1～10.6 GHz[1]内单一脉冲频谱利用率低,限制了设计脉冲的功率。通过多种脉冲组合设计UWB脉冲是一种有效方案。

文献[2]通过组合多个Schlotz脉冲设计UWB脉冲,但组合脉冲时域宽度较大,通信过程中易发生码间串扰(inter symbol interference,ISI),系统误码率偏高。文献[3-4]将3.1～10.6 GHz频段分块,在各频块内分别选取适合的高斯脉冲逼近FCC掩蔽,最后将各频块的脉冲组合成UWB脉冲。该方法设计参数易于获取,但高频段辐射功率偏低。文献[5]分析了以扁长椭球波脉冲为基函数的UWB脉冲的多址性能,但该脉冲在低频段的频谱利用率不足。文献[6]通过调整前三阶Rayleigh脉冲的成形因子来设计脉冲,虽然该脉冲频谱利用率优于高斯脉冲,但多址性能并不突出。文献[7-8]选用修正Hermite多项式(modified hermite polynominal, MHP)设计脉冲,因其基函数仅限于偶数阶MHP,限制了脉冲功率的灵活性,且多址接入性能仍有待改进。文献[9-10]分别利用正余弦波窄带信号设计UWB脉冲,所得脉冲在低信噪比环境中易受干扰。文献[11]将粒子群优化算法应用于超宽带脉冲设计,所得脉冲具有一定抗多址干扰(multiple access interference, MUI)性能,但用户数大于50时,MUI性能严重下降。另外文献[12]结合认知无线电理论提出了基于特征值分解的脉冲整形方案来抑制窄带通信系统对UWB通信的干扰,并以5.2 GHz 无线局域网络(wireless local area networks,WLAN)和8.5 GHz无线电定位服务为干扰源进行性能分析,但未对MUI性能进行分析。

为解决上述问题,本文选取各阶相互正交的MHP作为UWB脉冲设计的基函数,通过分析MHP时频特性,提出一种基于修正最小均方误差估计准则(minimum mean square error estimation, MMSE)的自适应迭代算法。该算法能兼容更多基函数并对脉冲功率谱密度(power spectral density, PSD)进行自适应调整,通过与广泛使用的脉冲设计方案进行仿真对比,验证了该算法设计脉冲的良好性能。

1 修正Hermite多项式

集成电路或双极性晶体管生成的超宽带脉冲[13]可用Hermite多项式近似逼近。各阶MHP相互正交且无直流分量,其表达式为

h0(t)=e-t2/4τ2

(1)

(2)

(3)

式(2)、式(3)的频域表达式分别为

(4)

(5)

式中,H0(f)、Hn+1(f)分别为h0(t)、hn+1(t)的傅里叶变换(Fourier transform, FT)形式。

前4阶MHP时域波形如图1所示。

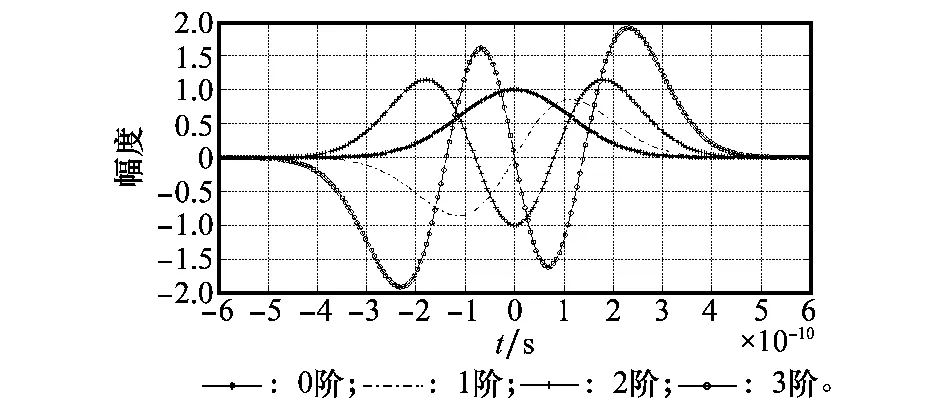
图1 前4阶Hermite脉冲时域波形(τ=0.8e-10)Fig.1 Time domain waveform of first 4 orders

由于衰减因子e-t2/4的衰减速度大于MHP增长速度,故各阶MHP时域脉宽趋于一致[14]。选取合理τ值,即可获得合适的脉冲宽度降低ISI。

由式(5)可推出

Hn(f)∝(j)nfne-4π2f2τ2

(6)

式中,f为频率。进一步推导可得峰值频率fpeak与τ的关系为

(7)

式(6)说明偶数阶MHP的FT为实函数,奇数阶的FT为虚函数。式(7)表明随着MHP阶数的增高,其峰值频率被搬移到更高频段。从图2的仿真结果可以看出:随着MHP阶数的增加,能量谱密度(energy spectral density,ESD)峰值将向更高频率端移动。

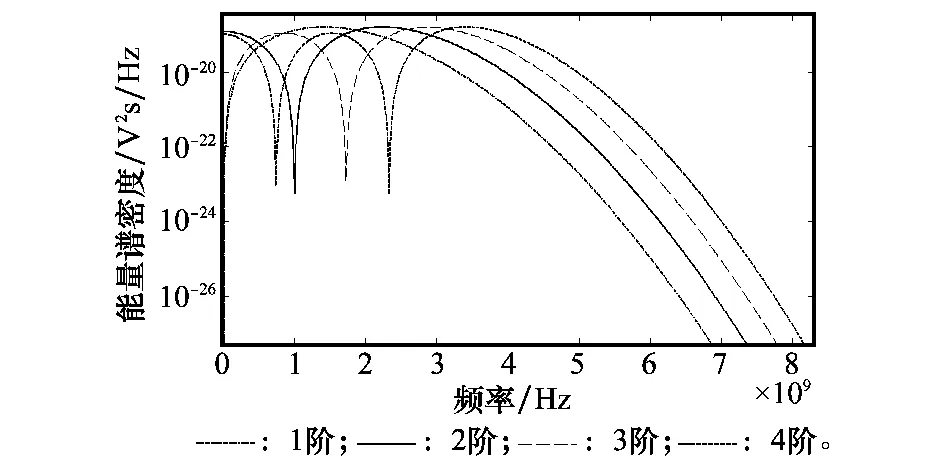
图2 前4阶Hermite脉冲的ESDFig.2 ESD of first 4 orders

图3和图4分别表示τ对MHP时域脉宽和频域ESD的影响:τ正比于MHP时域宽度,反比于ESD带宽。为保证设计脉冲的脉宽在1 ns以内,本文选取的各阶MHP均满足τ≤0.8e-10。

图3 τ对脉冲持续时间的影响Fig.3 Effect of τ on pulse duration

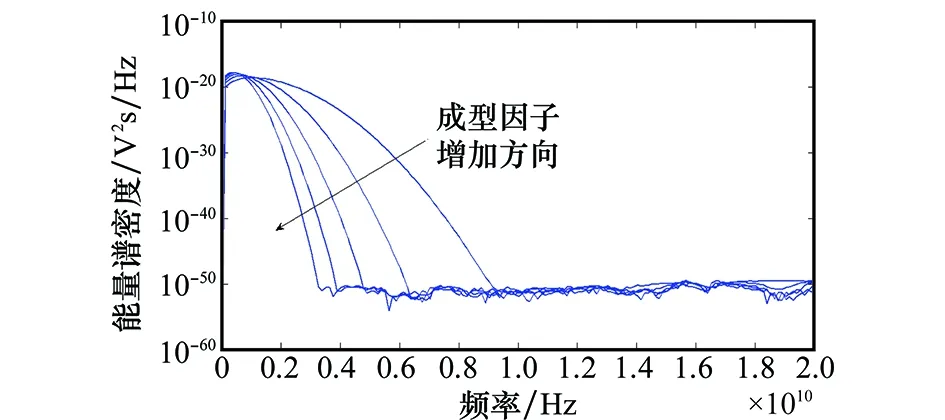
图4 τ对Hermite脉冲ESD的影响Fig.4 Effect of τ on ESD

2 UWB脉冲自适应迭代算法

2.1 基函数选取

记各阶MHP的权系数组成的向量为B=[β1,β2,β3,…βL]T。各阶MHP的FT组成的向量为G=[G1,τ1,G2,τ2,G3,τ3,…,GL,τL]T,其中L为设计脉冲中MHP的最大阶数,τ1,τ2,…,τL均小于0.8e-10。相应设计脉冲的功率谱密度为

(8)

(9)

式中,1≤i≤L。由于各阶MHP具有正交性,式(9)可近似表示[8]为

(10)

2.2 MMSE准则设计方案分析

MMSE准则是以误差平方和最小为前提寻找最佳拟合曲线的方法。其表达式为

(11)

式中,f(t)为目标函数。式(11)可改写为

(12)

按MMSE准则将设计脉冲的PSD向S(f)拟合,即求式(12)取得最小值时,设计脉冲中各阶MHP的权重向量为

Bmmse=[-1.726 4i,-0.578 1,1.053 3i,2.509 7,-2.785 1i,-1.712 4,1.101 9i,1.575 5,

1.860 0i,-1.334 1,1.026 1i,1.502 2,-1.805 7i, 1.279 1,0.788 5i]

图5为MMSE准则下设计脉冲PSD的拟合曲线。由于MMSE无法在具体频点对功率值加以约束,故图5中设计脉冲的低频段PSD大于目标函数。此外,由于奇数阶MHP的FT是虚函数,导致Bmmse中奇数项为虚数,因此奇数阶MHP实际上也无法用来进行实际的脉冲设计[8]。

图5 MMSE组合脉冲的PSD拟合曲线Fig.5 PSD fitting curve of MMSE combined pulse

2.3 基于修正MMSE的自适应迭代算法

为对图5中低频部分PSD进行修正并克服Bmmse中奇数项不能参与脉冲设计的问题,本文设计一种新的迭代选择算法。算法过程描述如下:

步骤 1 参数初始化:设定BF空间φ(本文φ由前15阶MHP组成)、迭代次数N、权重区间[α,β]、搜索步长Δ。

步骤 2 PSD曲线拟合:用随机数法和MMSE准则分别向FCC辐射掩蔽拟合,生成系数向量Brandom和Bmmse。

步骤 3 系数向量修正:生成新的系数向量E,其中E(i)=Bmmse(i),i=2,4,6,8，…;E(i)=Brandom(i),i=1,3,5,7，…。

步骤 4 对E进行自适应迭代:以E为初始权重生成初始组合脉冲,在[α,β]区间内对各BF的系数进行迭代,即对各频点做如下讨论:

首先定义迭代过程的约束条件为

ε(f)=S(f)-Sp(f)>0

(13)

步骤 4.1 式(13)成立则记录该组权值En,n为获得En时的迭代次数。按步骤1设定的步长Δ继续搜索,权值超出[α,β]或迭代次数达到N,则迭代终止。

步骤 4.2 式(13)不成立,则按式(14)给出的自适应公式对迭代步长进行自适应调整后继续迭代

(14)

式中,自适应因子μ的约束条件为μ≥1；ε(f)的约束条件由式(13)给出。

图6为步骤4所述初始脉冲的PSD,可以看到修正后的组合脉冲仍未满足式(13),为此迭代过程应侧重降低低阶MHP权重,并调节高阶MHP在低频段的分布,即通过式(14)增大低阶MHP的搜索步长同时降低高阶MHP在低频段搜索步长。图7为算法流程图。

图6 系数替换后的初始脉冲的PSDFig.6 PSD of initial pulse

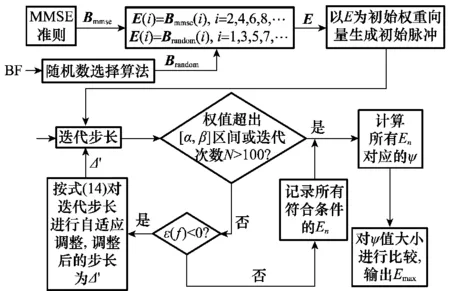
图7 基于MMSE修正的迭代算法流程图Fig.7 Flow chart of iterative algorithm

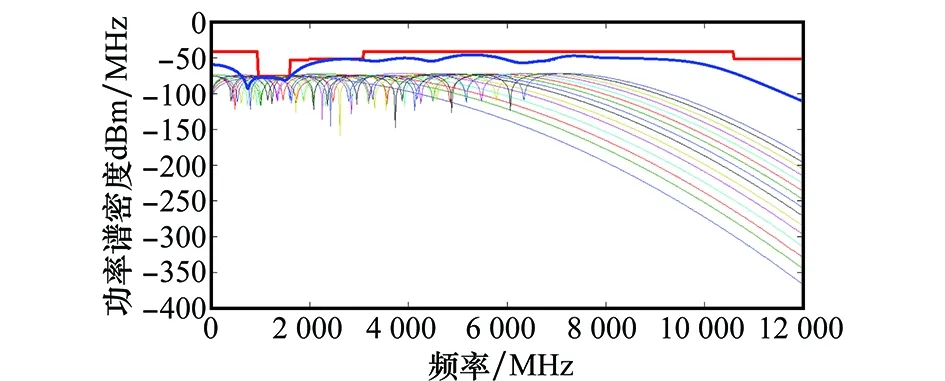
图8 设计脉冲的PSDFig.8 PSD of designed pulse

3 脉冲性能仿真

超宽带跳时(time hopping,TH)调制模型可表示为

(15)

r(t)=ru(t)+rmui(t)+n(t)

(16)

式中,ru(t)和rmui(t)分别代表接收机收到的有用信号和MUI噪声。在不同信道环境中用TH模型对接收端的多用户误码率(bit error rate, BER)和定时同步性能进行分析[15-16]。对比脉冲为文献[2]的正交Gaussian脉冲和文献[6]的Reyleigh脉冲。仿真参数设置为:数据流速率Rb=20 Mb/s,δ=0.5 ns,Tf=6。

3.1 接收端信号的误码率分析

用户数分别设置为10、20、100;信噪比仿真范围为[-5 dB,30 dB]。仿真结果如图9、图10所示。图9为不同信噪比下设计脉冲与Reyleigh脉冲的MUI性能比较。可以看出在用户数达到100时,设计脉冲的误码率仅为Reyleigh脉冲的15%。图10为设计脉冲与正交Gaussian脉冲的MUI性能对比。当用户数为100时,设计脉冲的误码率仅为正交Gaussian脉冲的60%;用户数为50时,设计脉冲的BER仅为正交Gaussian脉冲的40%;用户数为10时,设计脉冲的BER仅为正交Gaussian脉冲的2.7%。

图9 Reyleigh脉冲与设计脉冲误码率与信噪比关系对比图Fig.9 Comparison of Reyleigh pulse and design pulse

图10 正交Gaussian脉冲与设计脉冲误码率与信噪比关系对比图Fig.10 Comparison of orthogonal Gaussian pulse and design pulse

3.2 弱信号环境下同步性能分析

在信噪比为-20 dB的加性高斯白噪声 (additive white gaussian noise, AWGN)信道中,将一导频序列分别用本文设计脉冲、正交Gaussian脉冲和Reyleigh脉冲发射,在接收端检测信号的到达时间(time of arrival, TOA)估计,以比较各脉冲的定时同步性能。其中TOA真实值为:21.344 ns。各脉冲经信道传播后的TOA测量值如表1所示。

表1 各脉冲的TOA测量值

如表1所示,设计脉冲的定时同步误差低于另外两种脉冲,这说明设计脉冲在复杂信道中具有更好的鲁棒性。为对本文设计脉冲的相关性进行分析,将上述3种脉冲输入相关器,各脉冲的相关器输出如图11～图13所示。

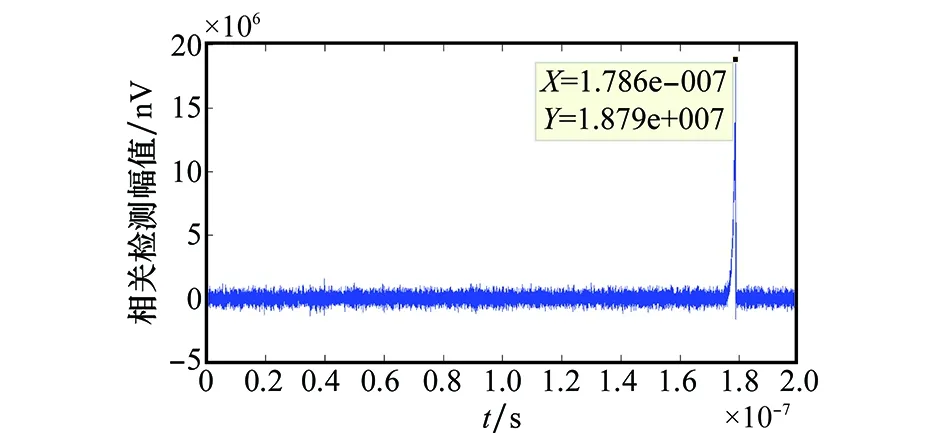
图11 Hermit脉冲的相关性能Fig.11 Correlator output of Hermit pulse

图12 正交高斯脉冲的相关性能Fig.12 Correlator output of quadrature Gauss pulse

图13 Reyleigh脉冲的相关性能Fig.13 Correlator output of Reyleigh pulse

图11～图13分别为设计脉冲、正交Gaussian脉冲和Reyleigh脉冲的相关器输出情况,通过分析可得:①在弱信号环境下设计脉冲的相关峰值高于另外两种脉冲,易于检测;②设计脉冲的噪底较薄,说明设计脉冲较另外两种脉冲具有更好的自相关和互相关性能。

4 结束语

针对UWB信号多址干扰和码间串扰问题,本文选用1到15阶Hermite脉冲作为BF进行UWB脉冲设计,通过分析MHP频域特性,选取了合适的τ值来控制脉宽,减小ISI干扰。在设计脉冲PSD曲线向辐射掩蔽拟合的过程中提出用随机系数来修正MMSE权重的方法,以此扩充参与脉冲设计的BF数量。采用自适应迭代算法来克服MMSE不能在具体频点上对设计脉冲PSD进行约束的问题。通过自适应地调整迭代步长来保证各频点上设计脉冲的PSD达到最佳拟合值。改变算法中自适应系数即可在算法计算量和拟合曲线NESP间取得平衡。最后从通信链路误码率入手,在多用户环境下对设计脉冲的性能进行仿真并与常用脉冲设计方案进行对比分析。仿真结果表明设计脉冲在获得较高的NESP的同时能保证通信链路具有较强鲁棒性。

[1] Keshavarz S N, Hajizadeh S, Hamidi M, et al. A novel UWB pulse waveform design method[C]∥Proc.oftheInternationalConferenceonNextGenerationMobileapplications,ServicesandTechnologies, 2010:168-173.

[2] Li L, Wang P, Wu X D, et al. Improved UWB pulse shaping method based on Gaussian derivatives[C]∥Proc.oftheIETInternationalCommunicationConferenceonWirelessMobileandComputing, 2011:438-442.

[3] Menon M B, Gopakumar A, Iqbal N V. A hybrid approach for UWB pulse shaping[C]∥Proc.ofthe2ndInternationalConerenceonElectronics&CommunicationSystems, 2015:263-270.

[4] Bowen B W, Nelson W S, Avise J C. Revision of part 15 of the commission’s rules regaring ultra-wideband transmission system[C]∥Proc.oftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, 1993, 90(12):5574-5577.

[5] Chen L L, Yu X, Dou Z. Research on the performance of the multiband impulse radio UWB communication system based on PSWF[J].JournalofHarbinEngineeringUniversity,2014, 35(4):499-503.(陈丽丽,于欣,窦峥.采用椭球波脉冲的多波段超宽带性能研究[J].哈尔滨工程大学学报,2014,35(4):499-503.)

[6] Chen R, Zeng X, Dong D. Algorithm for UWB pulse design and its performance analysis[C]∥Proc.oftheIEEEInternationalConferenceonIntegrationTechnology, 2007:74-77.

[7] Wu X L, Sha X J, Zhang N T. Modified Hermite function based pulse shaping algorithm for ultra wideband communications[C]∥Proc.oftheRadioandWirelessSysmposium, 2007:395-398.

[8] Lin D, Wu X L, Sha X J. Analysis on performance improvement in multiuser UWB system under imperfect power control[C]∥Proc.ofthe4thInternationalConferenceonWirelessCommunication,NetworkingandMobileComputing, 2008:1-4.

[9] Shi X. UWB waveform design method for arrowband interference suppression based on raised cosine pulse[C]∥Proc.oftheIEEEInternationalConferenceonComputerScienceandAutomationEngineering, 2011:646-649.

[10] Chen H, Jia Z, Cai X. Waveform design for UWB communication based on combined sinusoid Gaussian pulse[C]∥Proc.oftheInternationalConferenceonComputer,Mechatronics,andControntrolElectronicEngineering, 2010:267-271.

[11] Jia Z B, Chen H. A new UWB pulse design method and performance analysis[J].JournalofYunnanUniversity(NaturalSciencesEdition), 2013,27(2):162-166. (贾占彪, 陈红. 一种新的超宽带脉冲设计方法与性能分析[J].云南大学学报(自然科学版),2013,27(2):162-166.)

[12] El-Khamy R, Shaaban S, Ghaleb I, et al. An interference aware cognitive radio UWB(IA-CR-UWB) system using eigen pulse shaping[C]∥Proc.oftheInternationalConferenceonTechnologicalAdvancesinElectrical,ElectronicsandComputerEngineering, 2013:16-21.

[13] Gu L A. Research and design of ultra wideband pulse generation circuit[J].ModernElectronicsTechnique, 2016, 39(3): 131-134.(顾丽爱. 超宽带脉冲产生电路的研究与设[J].现代电子技术, 2016, 39(3): 131-134.)

[14] Wu X L, Qiu X, Ning X Y, et al. Orthogonal Hermite functions based orthogonal pulse shaping method[C]∥Proc.oftheElectricalandComputerEngineering, 2009:496-499.

[15] Mishra S, Rajesh A, Bora P K. Performance of pulse shape modulation of UWB signals using composite Hermite pulses[C]∥Proc.oftheNationalConferenceonCommunications, 2012: 1-5.

[16] Hidayat R, Miyanaga Y. IR-UWB pulse position modulation and pulse shape modulation through S-V channel model[C]∥Proc.oftheInternationalConferenceonCommunicationSoftwareandNetworks, 2010:214-217.

UWB pulse shaping algorithm in complex environment

SUN Xi-yan1,2, LIU Jian1, JI Yuan-fa1,2

(1.SchoolofInformationandCommunication,GuilinUniversityofElectronicTechnology,Guilin541004,China;2.GuangxiKeyLaboratoryofPrecisionNavigationTechnologyandApplication,Guilin541004,China)

In order to reduce the inter symbol interference (ISI) and multiuser interference (MUI) which exist in the ultra wideband positioning system under the multiuser and weak signal environment, an adaptive iterative algorithm based on minimum mean square error estimation (MMSE) for ultra-wideband (UWB) pulse design is proposed. Modified Hermite polynomial (MHP) is selected as the basis function of the designed pulse. By analyzing the time-frequency characteristics of MHP, coefficients of combined pulse are modified by the MMSE criterion. According to the fitting degree of power spectrum density between combined pulse and Federal communications commission (FCC) radiation masking, an adaptive algorithm is designed to realize pulse design. Simulation results show that the proposed scheme can obtain higher power utilization, and also obtain strong applicability in multiuser access and weak signal detection.

modified Hermite polynomial(MHP); adaptive iteration; multiuser interference (MUI); weak signal detection

2016-04-11；

2016-09-13；网络优先出版日期：2016-10-08。

国家自然科学基金(61162007，61271284，61362005，61561016)；广西自然科学基金(2013GXNSFA019004，2014GXNSFAA118352，2014GXNSFBA118280)；广西无线宽带通信与信号处理重点实验室主任基金；广西信息科学实验中心资助课题

TN 914, TN 781

A

10.3969/j.issn.1001-506X.2016.12.05

孙希延(1973-),女,研究员,博士,主要研究方向为卫星导航和电子对抗。

E-mail: sunxiyan1@163.com

刘 健(1991-),男,硕士研究生,主要研究方向为超宽带室内定位。

E-mail: sdjkjsdh@163.com

纪元法(1975-),男,教授,博士,主要研究方向为信号处理、卫星导航。

E-mail: jiyuanfa@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20161008.1500.006.html