拉挤成型复合材料板桩抗弯刚度简化计算

王仙美，王 俊，李 洋，刘伟庆，高龙刚

（1.江苏省交通规划设计院股份有限公司，江苏南京 210014；2.南京工业大学土木学院，江苏南京 211816）

拉挤成型复合材料板桩抗弯刚度简化计算

王仙美1，王 俊2，李 洋2，刘伟庆2，高龙刚1

（1.江苏省交通规划设计院股份有限公司，江苏南京 210014；2.南京工业大学土木学院，江苏南京 211816）

将折线型截面复合材料板桩整体刚度表示成翼缘和腹板刚度之和，基于层合板理论分层计算翼缘和腹板的局部刚度，然后提出整体结构抗弯刚度和抗剪刚度的简化计算公式，因此结构在弯曲荷载作用下的位移理论值可采用Timoshenko方程获得。开展拉挤复合材料板桩四点弯试验，将测量的荷载-位移曲线与理论值进行对比，表明本文推导的刚度计算公式在弹性范围内具有较好的精度，其中跨高比更大的试件理论与试验值更接近。该理论公式也可用于计算Z型、槽型、工字型等截面复合材料结构的刚度和位移。

复合材料;板桩;抗弯刚度;简化计算

1 引 言

目前常用的直立护岸结构从材料来分主要有：重力式浆砌块石圬工结构、钢筋混凝土板桩结构以及钢板桩结构等［1-2］。现有结构材料存在的主要问题有：圬工结构抗拉和抗剪强度低，混凝土易开裂继而钢筋锈蚀，钢板桩在氯离子的影响下易加速锈蚀。折线型纤维增强复合材料（FRP）板桩具有轻质高强，耐腐蚀和易施工等特点，在国外已成功应用于中小型护岸结构。然而折线型复合材料板桩属于薄壁结构，在使用时容易发生局部屈曲和整体变形过大，若加大截面的厚度和高度，则加大了生产难度和成本，上述弱点只有通过结构和材料的组合创新来克服。

目前国内外学者对拉挤复合材料板桩弯曲性能和耐久性进行了一系列研究。程瑶等［3-4］对复合材料板桩进行了一系列的性能试验，通过试验表明，板桩的破坏并非因应力破坏产生，而是由于变形过度所致。Cynthia Giroux等［5］通过对U形复合材料板桩弯曲试验研究，并基于Timoshenko梁理论和层合板理论，推导了板桩的弯曲和剪切刚度表达式。Bank［6］通过研究发现，复合材料的弹性模量较低，只有钢材的1/7左右，在荷载作用下容易产生较大变形而导致结构无法继续正常使用。Yixin Shao等［7］分别研究了在均布荷载作用下，单个U型截面板桩、在端部进行混凝土加固的板桩和三块混凝土加固相互拼接的板桩。Shao等［8］对拉挤成型复合材料板桩进行了三点弯荷载作用下的长期变形试验，并基于试验数据推导了数值分析模型。Shao等［9］探讨了复合材料板桩的吸水性及饱和吸水状态下的抗冻性能及拉伸性能。Honickman等［10］研究了在U型复合材料板桩中填充混凝土形成的组合梁抗弯性能。

本课题组在复合材料结构方面进行了较多研究：对U型截面GFRP-泡桐木夹层板进行了三点弯曲试验，研究表明该构造的U型板桩与国外现有的U型GFRP板桩相比，刚度提高了29.24％～181.97％［11］;双向纤维腹板格构能有效地提高夹层梁抗弯性能［12］;对在低速冲击作用下泡桐木夹层梁界面分层损伤机理进行研究，假定泡桐木芯材在低速冲击作用下，会发生分层连续屈曲破坏，同时结合理想弹塑性地基理论，建立了泡桐木夹层梁相应的界面分层损伤数值模型［13］;对折线型复合材料层合梁进行三点弯试验并建立折线型复合材料层合梁的整体抗弯刚度理论计算公式［14］。在上述研究基础上本文设计了翼缘和腹板均局部加强的复合材料板桩，为了简化设计程序，将折线型板桩结构的等效刚度看作翼缘和腹板的刚度之和，基于复合材料层合理论，建立板桩抗弯和抗剪刚度的计算方法。因此可用Timoshenko梁理论计算具有不同边界的复合材料板桩构件弯曲挠度。开展四点弯试验，并将理论计算荷载-位移曲线与试验值进行对比。

2 复合材料板桩刚度计算理论

2.1 截面简化

本文设计的复合材料Z型板桩，翼缘和腹板均进行了局部加强，两块Z型板桩可通过C-T锁扣拼成帽型，如图1所示。由于结构的计算截面比较复杂，对截面进行了如下简化：（1）不考虑腹板和翼缘的连接处的倒圆角;（2）忽略腹板加强肋;（3）忽略下翼缘的锁扣，将上翼缘的锁扣连接变成平板连接。简化后截面如图2所示。

图1 拼装成帽型的Z型板桩截面图Fig.1 Cap cross section assembled by Z-shape sheet pile

图2 简化后的截面图Fig.2 Simplified cross section

2.2 刚度计算

2.2.1 抗弯刚度 根据相关的研究，复合材料折线型板桩的整体等效抗弯刚度（EI）s等于各部分抗弯刚度之和，因此可得：

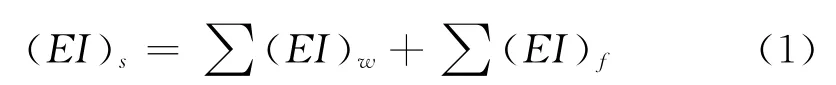
其中（EI）s为整个截面的抗弯刚度，（EI）w为腹板抗弯刚度，（EI）f为翼缘板抗弯刚度。

翼缘各部分到中心轴的距离分别为（如图3所示）：

其中h为上下翼缘板之间的净高，d为中性轴距h/2的距离（图为中性轴在h/2处，故d=0），tw为翼缘板的厚度，t为翼缘板加厚部分的单边厚度。

图3 翼缘板部分截面示意图Fig.3 Cross section of a flange

因此可以推导翼缘板的抗弯刚度为：

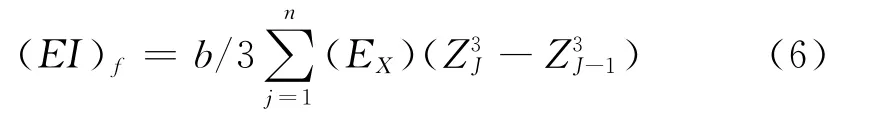
同理根据图4可推导腹板的抗弯刚度

其中h为腹板的厚度，θ为腹板的竖直倾角（本文设计的板桩腹板厚度与翼缘厚度相等）。

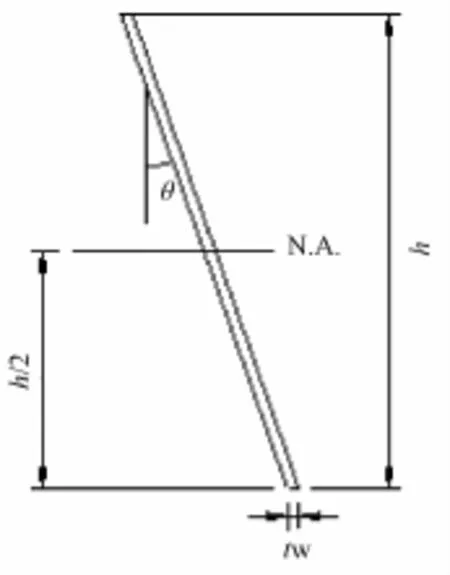
图4 腹板截面示意图Fig.4 Cross section of a web

2.2.2 抗剪刚度 根据梁跨中剪切变形w与中性轴处（τxz）z=0关系式：

其中：（τxz）z=0为腹板中性轴处剪应力;V为截面剪力; G为腹板剪切模量;k为切应变的截面形状系数;k AG为等效剪切刚度。

由轴向剪力平衡可得：

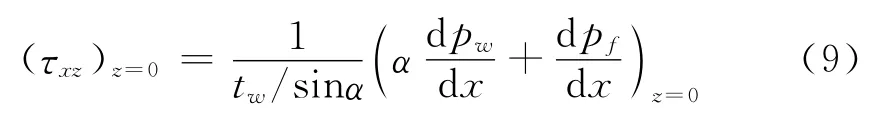
其中：pw为中性轴一侧的腹板的轴向合力;pf为中性轴一侧的翼缘板的轴向合力;α为中性轴处腹板的个数。

对于翼缘板沿Z轴方向积分，可得：

令

则：

同理，对于腹板沿Z方向积分，可得：

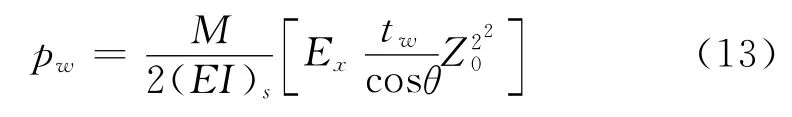
令

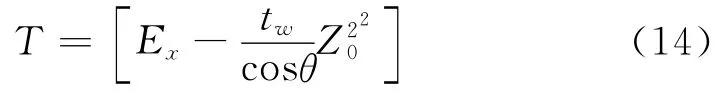
则：

剪应力只作用在中性轴上，而只有腹板通过中性轴，因此截面的剪切模量为：

将式（12）和式（15）代入式（9），再代入到式（8），消去V，得：

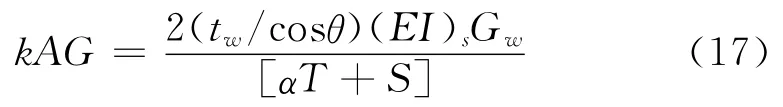
根据Timoshenko梁公式四点弯梁的位移可表示成

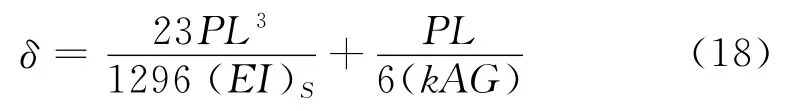
其中：δ为跨中竖向位移;（EI）S为构件弯曲刚度;（k AG）为构件等效剪切刚度;P为荷载;L为构件计算跨度。

3 四点弯试验概述

本试验共有4对Z型试件，两两拼接成U型截面进行抗弯试验（如图5所示）。构件采用拉挤工艺制作，其基体为间苯不饱和树脂，纤维采用无碱玻璃纤维丝和双向布。试件设计如表1所示。试验加载设备为油压千斤顶-反力架，采用夹具对试验构件的加载点和支撑点进行约束。用油压千斤顶对试件加载，在千斤顶加载头上安装的传感器将加载数据传送给应变仪。用有效量程为200mm的位移计来测量试件的跨中位移。

图5 弯曲试验装置图Fig.5 Test set-up

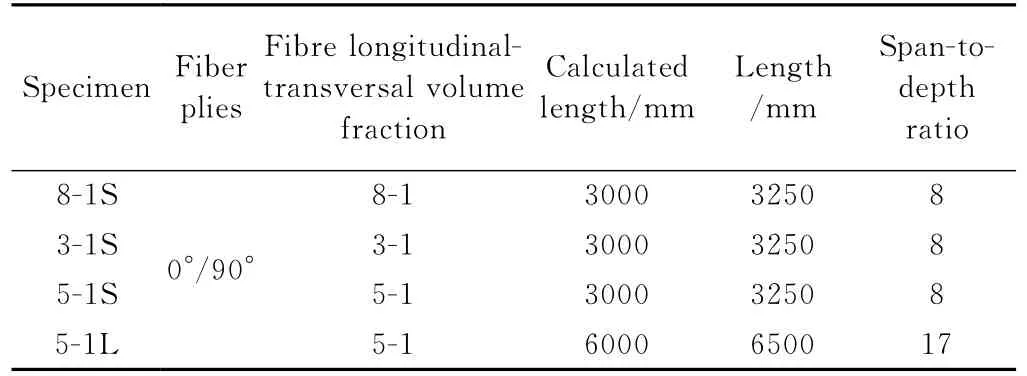
表1 试验设计Table 1 Summary of test matrix

拉伸试件取样和试验参照GB/T 1447-2005《纤维增强塑料拉伸性能试验方法》进行。材料性能试验结果见表2。

表2 材料性能试验结果Table 2 Mechanical properties of tested specimens

4 实验值与理论值的对比

根据试验测得的跨中挠度与上述理论公式计算值对比的荷载-位移曲线如图6所示。对于跨高比8的构件，实测刚度与理论值相比偏小，这是因为四点弯试验引起了加载部位局部破坏，造成构件刚度没有完全发挥。而跨高比17的构件实测荷载-位移曲线与理论值吻合较好，这是因为局部破坏对长跨结构的刚度影响较小。

图6 理论和试验荷载-位移曲线对比Fig.6 Comparison of load-deflection curves between theoretical and test results

5 结 论

基于复合材料层合板理论，以帽子型截面为例推导了复合材料板桩弯曲刚度和等效剪切刚度的计算公式。通过与拉挤复合材料板桩试件四点弯荷载-位移曲线在线弹性范围的理论和试验值对比，表明本文推导的刚度计算公式具有较好的精度。该理论计算公式也可适用于计算Z型、槽型、工字型等截面复合材料结构的刚度和位移。

［1］饶思梁.内河航道尺度与通航能力关系研究［D］.武汉：武汉理工大学，2011.

［2］徐朝辉，步海滨，程巍华，陈志强.内河航道生态护岸的发展及应用分析［J］.水运工程，2009，9：107～110.

［3］程瑶，徐舜华.FRP复合板桩性能试验研究［J］.路基工程，2007，133（4）：72～73.

［4］程瑶，徐舜华.FRP板桩墙变形计算方法探讨［C］.第一届中国水利水电岩土力学与工程学术讨论会论文集.2006.

［5］Giroux C，Shao Y.Flexural and shear rigidity of composite sheet piles.Flexural and shear rigidity of composite sheet piles［J］. Journal of composites for construction，2003，7（4）：348～355.

［6］Bank LC.Flexural and shear moduli of full section fiber reinforced plastic（FRP）pultruded beams［J］.Journal of testing and evaluation，1998，（17）：40～45.

［7］Shao Y，Shanmuga J.Moment capacities and deflection limits of PFRP sheet piles［J］.Journal of Composites for construction，2006，10（6）：520～528.

［8］Shao Y，Shanmugam J.Deflection creep of pultruded composite sheet piling［J］.Journal of composites for construction，2004，8（5）：471～479.

［9］Shao Y，Kouadio S.Durability of fiberglass composite sheet piles in water［J］.Journal of composites for construction，2002，6（4）：280～287.

［10］Honickman H，Fam A.Investigating a structural form system for concrete girders using commercially available GFRP sheetpile sections［J］.Journal of composites for construction，2009，13（5）：455～465.

［11］王俊，刘伟庆，胡世俊，方海，周宏伟.U型截面GFRP-泡桐木夹层板抗弯性能试验研究［J］.建筑材料学报，2014，2：379～386.

［12］刘子健，刘伟庆，万里，方海，陆伟东.双向纤维腹板增强夹层结构的弯曲性能［J］.材料科学与工程学报，2013，4：544～549.

［13］龚海亮，刘伟庆，万里，余轶.低速冲击作用下泡桐木夹层梁界面分层损伤机理［J］.材料科学与工程学报，2013，5：723～727.

［14］张界杰，王俊，刘伟庆，等.折线型截面复合材料层合梁弯曲性能预测与分析［J］.材料科学与工程学报，2014，3：456～460.

An Approximate Algorithm of Bending Stiffness of pultruded FRp Sheet piles

WANG Xian-mei1，WANG Jun2，LI Yang2，LIU Wei-qing2，GAO Long-gang1
（1.Jiangsu province Communication planning and Design Institute Limited Company，Nanjing 210014，China; 2.Civil Engineering，Nanjin Tech University，Nanjing 211816，China）

The stiffness of FRP sheet pile with polyline-section shape can be expressed as the sum of the stiffness of both the flange and the web.Based on classical laminate theory，the local stiffness of each flange and web can be obtained，respectively，and then a simplified formula was derived to predict the bending stiffness and shear stiffness of the whole structure.Moreover，the deformation of the structure under fourpoint bending load could be obtained by Timoshenko’s equation.Four-point bending experiment was conducted to measure the load-deflection curves.The comparison between theoretical and experimental results shows that the predicted bending stiffness and shear stiffness agree well with those obtained from the experiments in the elastic phase.It is indicated that the experimental loading-deformation curves of specimens with higher spandepth ratios fit better with the theoretical results than those of specimens with lower span-depth ratios.The present method can also be used to calculate the bending stiffness and shear stiffness of FRP structures with cross section of Z shape，groove shape or H shape.

FRP composites;sheet pile;bending stiffness;approximate algorithm

TB332

A

10.14136/j.cnki.issn 1673-2812.2016.03.023

1673-2812（2016）03-0450-05

2015-03-26;

2015-07-09

国家自然科学基金重点项目资助项目（51238003）、国家自然科学基金资助项目（51308288）、江苏省交通科学研究计划资助项目（2013 T02-2）

王仙美（1964-），女，研究员级高级工程师，主要从事港口航道与海岸工程管理与设计。

王 俊（1976-），女，副教授，硕士生导师，主要从事新型复合材料结构研究。E-mail：wangjun3312@njtech.edu.cn。