谱元法应用于涡声传播问题的研究

包振忠,秦国良,耿艳辉,和文强

(西安交通大学能源与动力工程学院,710049,西安)



谱元法应用于涡声传播问题的研究

包振忠,秦国良,耿艳辉,和文强

(西安交通大学能源与动力工程学院,710049,西安)

为了满足计算气动声学对低色散、低耗散高精度数值离散格式的需求,将高精度谱元法结合声比拟理论应用于求解气动声学问题。以伪声压的时间二阶导数作为非齐次波动方程的声源项,空间离散采用谱元法,时间离散应用隐式Newmark法,并在外边界采用C-E-M吸收边界条件,求解了由两个相距为2r0的等环量点涡组成的同向旋转涡对的发声问题。旋转涡对的不可压缩流场通过复位势理论获得,声源由流场量计算得来,并将数值结果与应用多级匹配展开法得到的解析解进行比较,可得数值解与分析解吻合较好。研究结果表明:应用高精度谱元法进行空间离散时,每波长的网格数为11时可达到很高的精度;网格数一定的情况下,时间步长越小得到的数值解与分析解之间的误差就越小;另外,证明了将伪声压对时间的二阶导数作为声源项,能够高精度求解不可压缩流动引起的气动声学问题。

计算气动声学;谱元法;声比拟理论;吸收边界条件;有限元;同向旋转涡对

随着各种交通工具速度的快速提升,辐射的气动噪声也急剧增大。气动噪声不仅引起环境污染甚至还会造成结构的疲劳和破坏,会对人的生理和心理构成严重影响。随着计算流体力学(CFD)的飞速发展,数值模拟被广泛应用于工程实践,但传统的CFD方法无法满足气动声学问题的研究,计算气动声学(CAA)对计算格式提出了比较苛刻的要求[1-2]。由于声波在传播过程中衰减很慢且声学量相对于流动量在量级上要小得多,这就要求数值方法本身必须是高精度数值方法,其数值噪声要尽量小,避免声波脉动量被数值误差所掩盖,即该高精度方法具有极低的数值色散和耗散以确保能够高精度模拟声波的长距离传播。另外,传统的CFD所求解的区域较小,数值模拟总在有限的区域内进行,声波在传播过程中具有低耗散特性相较于流场的数值模拟,声场的数值模拟需要更多的计算花费。为减少计算量,声波在计算域开放边界必须能无反射出入,采用适当的吸收边界条件[3]才能达到这一效果。

湍流产生的噪声大都起源于流动中的涡结构,因此在计算气动声学中常使用涡源作为人工声源来分析噪声产生的机理[4]。双涡流动结构是复杂流场中的常见现象,大型民机增升装置后缘襟翼侧缘所卷起的旋涡即为典型的双涡流动[5]。Manfred等用有限元法求解了不可压缩N-S方程和非齐次波动方程,结合声比拟理论将流场信息插值到声场网格中,得到了双涡流动发声的数值解[6-7]。Zhu等采用高阶有限差分格式结合黏声分离法对双涡流动发声问题进行了数值模拟[8-9]。Farshchi等采用线性和非线性黏声分离技术,并使用高阶色散保持格式进行数值离散,求解了双涡流动发声问题,结果表明,线性计算在保持计算精度的条件下大幅降低了计算时间[10]。Ekaterinaris发展了黏声分离技术,并用高阶迎风格式对控制方程进行了离散求解,验证了数值格式具有较好的数值精度[11-12]。

本文基于Chebyshev谱元法对控制方程进行空间离散,时间离散应用隐式Newmark法并结合声比拟理论从流场中提取声源,对同向旋转涡对的发声问题进行了数值模拟,并研究了数值精度的影响因素[13-14],为更好地求解计算气动声学问题提供了一定的理论依据。

1 控制方程

自1952年Lighthill提出声比拟理论以来,Lighthill方程

(1)

在气动声学问题中得到广泛应用,其中Tij为Lighthill应力张量,在绝热无黏的情况下表达式为

Tij=ρuiuj

(2)

p′=pi+pa

(3)

由不可压缩连续性方程和动量方程可得伪声压,满足条件[16]

(4)

将式(4)代入式(1)可得

(5)

式(5)提供了一种只用伪声压的二阶时间导数即可作为声源来计算声压的方法,该方法等价于文献[9]中所提的黏声分离法,初始条件为

(6)

2 数值算法

对边界条件的处理是声波传播的一个关键问题,由于计算机资源和区域的限制,所以在数值模拟波动问题时需要对求解区域进行边界截断。由于截断在边界处会引起波的反射,影响数值求解区域,为了减小波的反射,本文采用C-E-M吸收边界条件[17]

(7)

结合吸收边界条件,式(5)相应的Galerkin变分形式为

∀pa,w∈H1(Ω),t∈[0,T]

(8)

式中:ΓI为边界;w为检验函数。

小学语文阅读文章的篇幅比较短，大多是几段，每一段也由几句话组成。从文章整体上看，完整的文章由段落组成，段落则由句子组成，句子由词语或者文字组成。因此，培养学生的综合阅读能力，需要关注词句基础训练。

2.1 空间离散

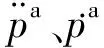
(9)

式中:M、C、K、S分别为质量矩阵、阻尼矩阵、刚度矩阵和源项,具体离散过程和表达式可参见文献[18]。

2.2 时间离散

式(9)在时域上的求解一般有隐式和显式两种逐步积分途径,显式逐步积分方法一般是条件稳定的,隐式方法是绝对稳定的。考虑到算法的稳定性,本文选择隐式Newmark方法,递推公式为

(10)

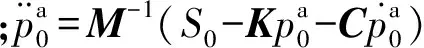
3 数值算例

3.1 数值模型

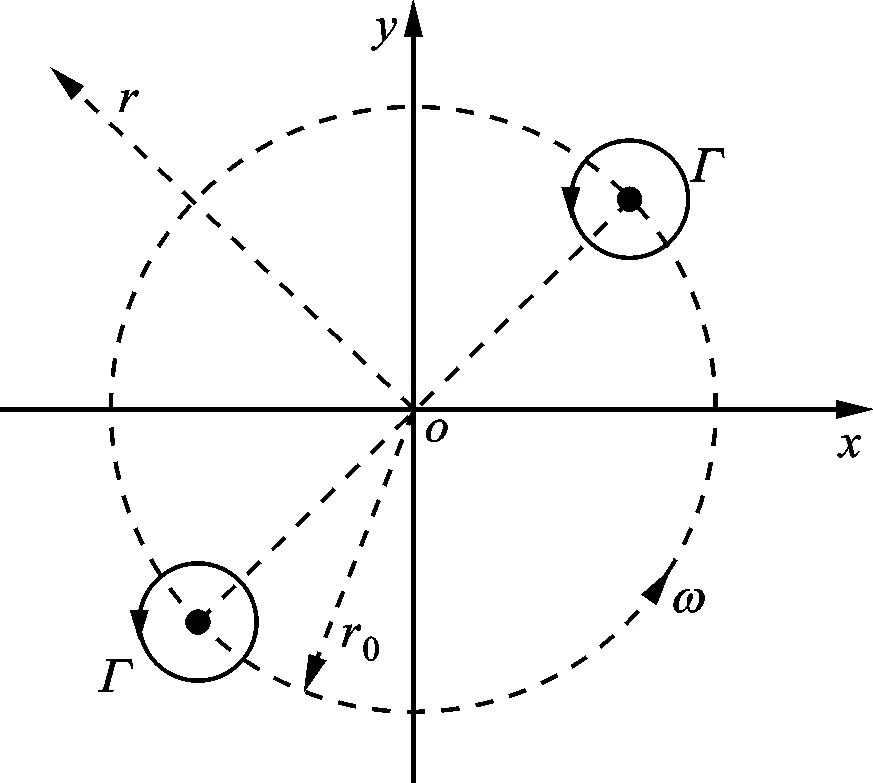
图1 同向旋转涡对配置

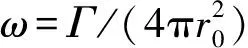
在不可压缩、无黏的条件下,涡对产生的流场可用复位势函数来表示,即

(11)

式中:z=x+iy=reiθ;b=r0eiωt。

由式(11)可得计算声源时需要的流场量

(12)

声压波动的分析解[18]可通过匹配渐近展开法获得,即

(13)

式中:k=2ω/c0;J2(kr)、Y2(kr)分别为第1、2类二阶贝塞尔函数;ψ=2(ωt-θ)。

计算区域选为400 m×400 m的方形区域,将源项区域限定在中间范围的200 m×200 m区域。总节点数Nd=(NmNx+1)(NnNy+1),旋转半径r0=1 m,环量Γ=1.005 31 m2/s,声速c0=1 m/s,波长λ≈39 m,Mr=0.079 6。本文在模拟中取均匀单元,单元内的插值节点数为2,在全部区域的网格都为均匀网格。

3.2 数值结果

图2给出了式(5)中的源项在t=100 s时的云图和三维图,其中时间步长Δt=0.1 s,网格间距Δx=3.64 m,此时每波长的网格数约为11。由图2可看出四极子源项的特征,且源项区域足够大,使得截断处源项的幅值远小于最大值,仅为其0.25%;原点处具有奇异性,源项梯度特别大。为了消除这一奇异性,Manfred等采用Scully涡核模型[19],Ekaterinaris等采取了对原点附近的源项进行截断的办法[12]。本文采用文献[12]的方法,即r/r0≤1.5时不存在源项。

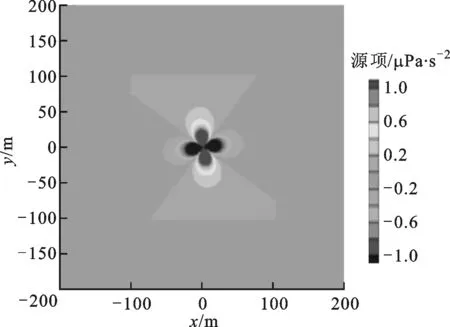
(a)源项云图

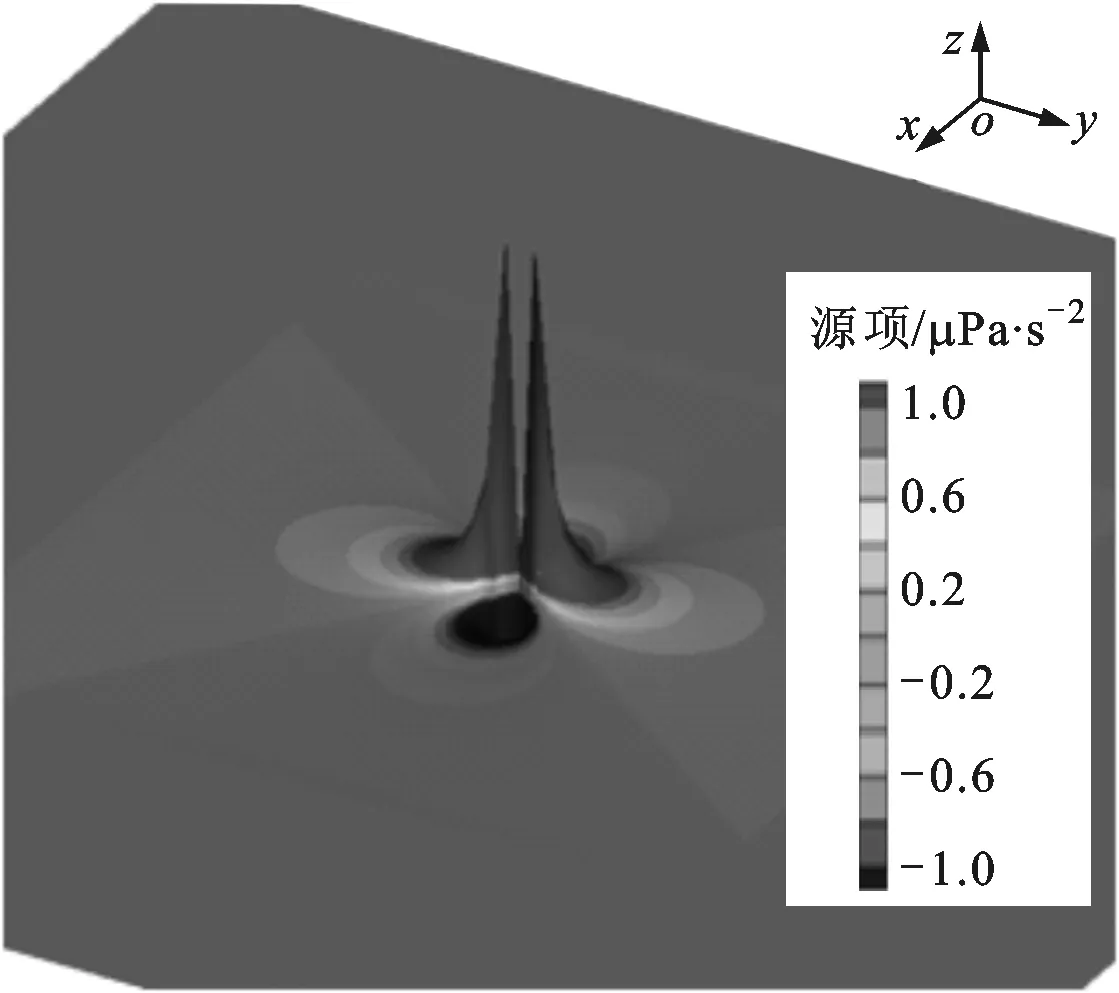
(b)源项三维图图2 源项分布图

同向旋转涡对在240 s时产生的声压场如图3所示。由图3可看出,产生的声场为旋转的双螺旋形结构,吸收边界条件的应用可吸收外向声波,不影响声场中解的精度,声波传递出去基本没有引起反射。

(a)同向旋转涡对声场云图

(b)同向旋转涡对声场三维图图3 240 s时同向旋转涡对声场

为了比较不同网格间距对数值结果的影响,分别计算了Δx=9.52,6.45,3.92,2.82 m、Δt=2.0 s时的声场,声压沿x正半轴方向的变化情况如图4所示。随着传播距离的增加,声压总体呈现衰减的趋势。Δx=9.52 m时,由于其网格间距太大,与其他节点数时的解有明显偏差,其他声压型线整体基本一致,幅值和相位都没有太大偏差。

图4 不同网格间距时x方向的声压型线

Δx=3.64 m、不同时间步长时声压沿x正半轴方向的变化曲线如图5所示。由图5可看出,在靠近原点附近数值解与分析解差别较大,这是由消除原点奇异性对源项的截断所引起的。另外,随着时间步长的减小,声压型线与分析解之间的差别也越来越小,但是幅值仍稍微低于分析解,可能和谱元算法在计算离散波动方程时的耗散有关。色散误差除了在Δt=2.0 s时较大,其余时间步长均很小,与分析解吻合较好。具体谱元方法求解波动方程及数值精度的相关因素分析可参照文献[20]。

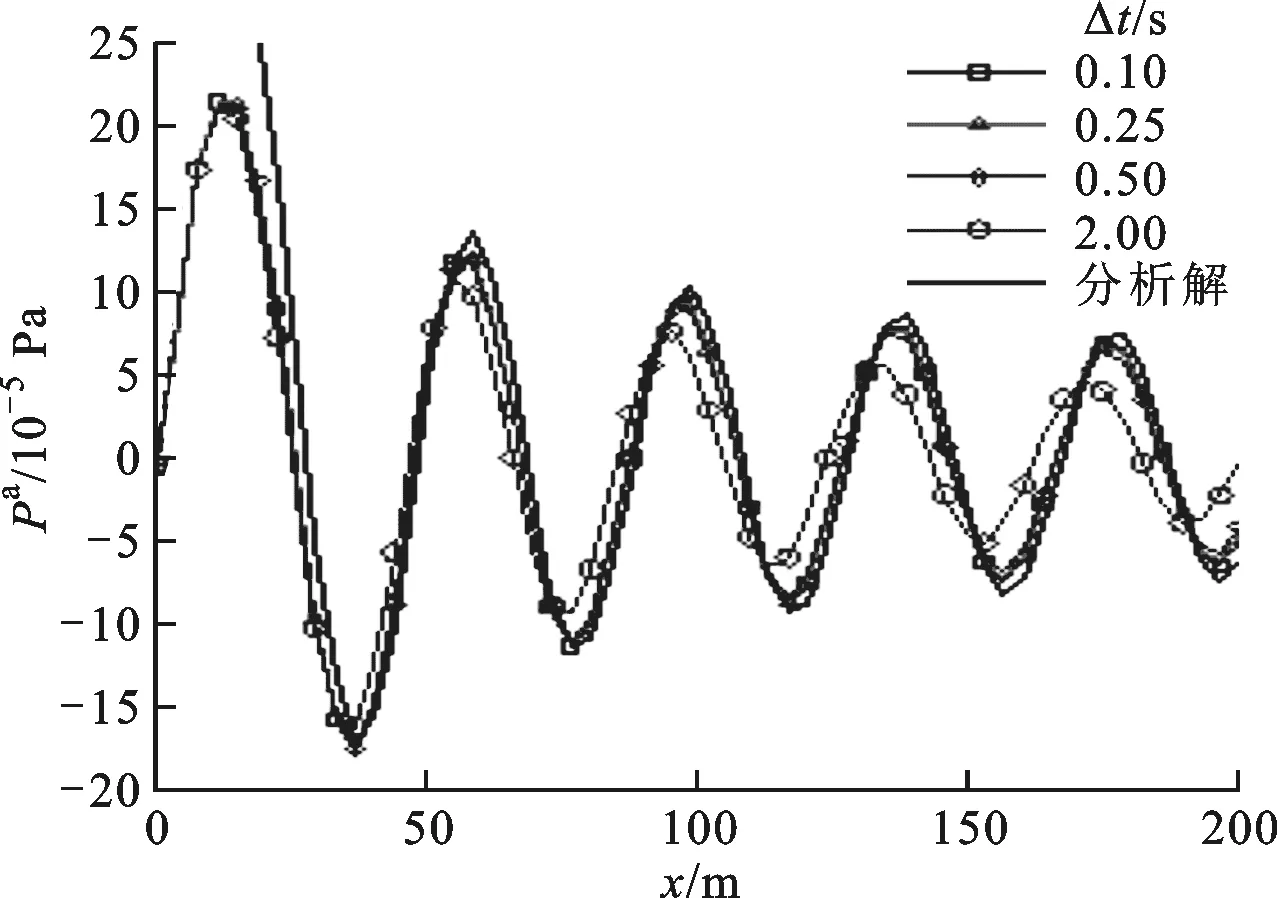
图5 不同时间步长时x方向的声压型线

(0,58.2)点处声压数值解和分析解随求解时间的变化如图6所示,原点附近的声波到达该点后,声压数值解与分析解匹配很好,只有在波峰与波谷处略微小于分析解。这是由为消除原点奇异性对源项进行截断,而导致总体源项偏小所引起的。240 s处声压数值解与分析解的比较如图7所示。由图7可看出,数值解与分析解的相位、幅值都比较吻合,在分界线处没有明显的数值跳跃。

图6 (0,58.2)点处声压随时间的变化

图7 240 s时数值解与分析解的比较

4 结 论

本文实现了将高精度谱元法结合声比拟理论应用于求解气动声学的问题,并对由两个点涡形成的同向旋转涡对声场进行了数值模拟。为了分析影响数值精度的原因,计算了不同网格、不同时间步长情况下的声场,并将计算结果与用多极匹配展开法得来的分析解进行了对比。结果表明:应用谱元法进行空间离散时,采用极少的节点数就可达到很高的精度;节点数一定的情况下,时间步长越小得到的数值解与分析解之间的误差越小,但花费的计算资源越多。用数值算例验证了将伪声压对时间的二阶导数作为声源项,可用来求解不可压缩流动引起的气动声学问题。

[1] 李晓东, 江旻, 高军辉, 等. 计算气动声学进展与展望 [J]. 中国科学: 物理学·力学·天文学, 2014(3): 234-248. LI Xiaodong, JIANG Min, GAO Junhui, et al. Progress and prospective of computational aeroacoustics [J]. Science China: Physics, Mechanics & Astronomy, 2014(3): 234-248.

[2] LELE S K, NICHOLS J W. A second golden age of aeroacoustics [J]. Philosophical Transactions of the Royal Society of London: A Mathematical, Physical and Engineering Sciences, 2014, 372(2022): 20130321.

[3] GIVOLI D. High-order local non-reflecting boundary conditions: a review [J]. Wave Motion, 2004, 39(4): 319-326.

[4] DAHL M D. Numerical solutions to the fourth and second computational aeroacoustics (CAA) workshop benchmark problems [C]∥The 4th Computational Aeroacoustics (CAA) Workshop on Benchmark Problems. Washington, DC, USA: NASA Glenn Research Center, 2004: 187-197.

[5] 徐康乐, 陈迎春, 陶俊, 等. 低马赫数条件下气动声场流场分裂求解方法研究 [J]. 复旦学报(自然科学版), 2014, 53(5): 636-644. XU Kangle, CHEN Yingchun, TAO Jun, et al. A splitting simulation method for aeroacoustic at low Mach conditions [J]. Journal of Fudan University(Natural Science), 2014, 53(5): 636-644.

[6] HÜPPE A, KALTENBACHER M. Spectral finite elements for computational aeroacoustics using acoustic perturbation equations [J]. Journal of Computational Acoustics, 2012, 20(2): 1240005.

[7] ALI I, ESCOBAR M, KALTENBACHER M, et al. Time domain computation of flow induced sound [J]. Computers & Fluids, 2008, 37(4): 349-359.

[8] ZHU W J, SHEN W Z, SØRENSEN J N. High-order numerical simulations of flow-induced noise [J]. International Journal for Numerical Methods in Fluids, 2011, 66(1): 17-37.

[9] HARDIN J, POPE D. An acoustic/viscous splitting technique for computational aeroacoustics [J]. Theoretical and Computational Fluid Dynamics, 1994, 6(5/6): 323-340.

[10]FARSHCHI M, HANNANI S K, EBRAHIMI M. Linearized and nonlinear acoustic/viscous splitting techniques for low Mach number flows [J]. International Journal for Numerical Methods in Fluids, 2003, 42(10): 1059-1072.

[11]EKATERINARIS J A. New formulation of Hardin-Pope equations for aeroacoustics [J]. AIAA Journal, 1999, 37(9): 1033-1039.

[12]EKATERINARIS J A. An upwind scheme for the computation of acoustic field generated by incompressible flow [J]. AIAA Journal, 1997, 35(1): 14481455.

[13]ZHU C, QIN G, ZHANG J. Implicit Chebyshev spectral element method for acoustics wave equations [J]. Finite Elements in Analysis and Design, 2011, 47(2): 184-194.

[14]ZHANG R, QIN G, ZHU C. Spectral element method for acoustic propagation problems based on linearized Euler equations [J]. Journal of Computational Acoustics, 2009, 17(4): 383-402.

[15]RIBNER H S. The generation of sound by turbulent jets [J]. Advances in Applied Mechanics, 1964, 8: 103182.

[16]PAPAGEORGAKOPOULOS J, TSANGARIS S. A numerical method for predicting acoustical wave propagation in open spaces [J/OL]. [2016-04-06]. https:∥www.hindawi.com/journals/isrn/2011/174031/abs/.

[17]CLAYTON R, ENGQUIST B. Absorbing boundary conditions for acoustic and elastic wave equations [J]. Bulletin of Seismological Society of America, 1977, 67(6): 1529-1540.

[18]张荣欣, 秦国良. 用切比雪夫谱元方法求解均匀流场中的声传播问题 [J]. 西安交通大学学报, 2009, 43(7): 120-124. ZHANG Rongxin, QIN Guoliang. Chebychev spectral elements method for acoustic propagation problem in a uniform mean flow [J]. Journal of Xi’an Jiaotong University, 2009, 43(7): 120-124.

[19]LEE D J, KOO S O. Numerical study of sound generation due to a spinning vortex pair [J]. AIAA Journal, 1995, 33(1): 20-26.

[20]朱昌允, 秦国良, 徐忠. 谱元方法求解波动方程及影响其数值精度的相关因素 [J]. 西安交通大学学报, 2008, 42(1): 56-59. ZHU Changyun, QIN Guoliang, XU Zhong. Implicit spectral element method for wave equation and some factors influencing numerical accuracy [J]. Journal of Xi’an Jiaotong University, 2008, 42(1): 56-59.

(编辑 赵炜 荆树蓉)

Investigation of Vortex Sound Propagation Using Spectral Element Method

BAO Zhenzhong,QIN Guoliang,GENG Yanhui,HE Wenqiang

(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

In order to meet the requirements of low dispersive and low dissipative numerical discretization schemes in computational aero-acoustics, the spectral element method combined with Lighthill’s acoustic analogy theory for the simulation of aeroacoustic problems is investigated. Taking the second temporal derivative of pseudopressure as the source of the inhomogeneous wave equation, and space discretization using spectral element method time discretization using implicit Newmark method, under the C-E-M absorbing boundary condition the acoustic field generated by a co-rotating spinning vortex pair is solved. This co-rotating vortex pair consists of two point vortices separated by a fixed distance of 2r0with a circulation intensityΓ. The incompressible flow field is obtained using the complex potential theory, and the acoustic source terms are computed using these hydrodynamic quantities. The acoustic pressure results are evaluated by comparing them with the analytical solution obtained from the matched asymptotic expansion (MAE) method The numerical solutions are in good agreement with the analytical solutions. The results show that the spectral element method can obtain high accuracy using only eleven grids in one wavelength. In the case of the same number of grids, the smaller the time step, the smaller the error between numerical solution and analytical solution. Finally, it is proved that the aero-acoustic problems induced by incompressible flows can be solved with high accuracy by using the second temporal derivative of the pseudopressure as the acoustic source.

computational aero-acoustics; spectral element method; acoustic analogy theory; absorbing boundary condition; finite element method; co-rotating spinning vortex pair

2016-05-20。 作者简介:包振忠(1992—),男,博士生;秦国良(通信作者),男,教授,博士生导师。 基金项目:国家重点基础研究发展计划资助项目(2012CB026004)。

时间:2016-09-14

10.7652/xjtuxb201611017

O121.8;G558

A

0253-987X(2016)11-0110-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160914.1803.002.html