一种求解含围带阻尼成圈叶片振动响应的高效方法

邱恒斌,徐自力,刘雅琳,上官博

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安建筑科技大学环境与市政工程学院,710055,西安;3.西安热工研究院有限公司,710032,西安)



一种求解含围带阻尼成圈叶片振动响应的高效方法

邱恒斌1,徐自力1,刘雅琳2,上官博3

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安建筑科技大学环境与市政工程学院,710055,西安;3.西安热工研究院有限公司,710032,西安)

针对含围带阻尼成圈叶片的非线性振动响应计算时自由度多、迭代求解计算量大的问题,综合波传动法、高阶谐波平衡法及Receptance法推导了一种求解含围带阻尼成圈叶片振动响应的高效方法。根据成圈叶片结构周期对称的特点,采用波传动法,将含围带阻尼成圈叶片降阶为一个基本扇区进行振动分析,接触面的非线性摩擦力可由单个扇区的位移结合干摩擦模型求得;将降阶后单个扇区的时域振动微分方程由高阶谐波平衡法转化为频域代数方程,通过叶片正则振型的正交性对频域的振动方程进行解耦,并利用叶片局部非线性的特点对非接触面上的线性自由度进一步缩聚,从而减少非线性迭代的规模,提高计算效率。算例结果表明:采用所提求解方法的响应计算结果与采用整体模型的结果相差小于0.33%,计算时间缩短为原来的10%,验证了该方法的正确性、高效性,同时采用该方法研究了真实围带阻尼叶片的非线性振动响应。

成圈叶片;振动响应;围带阻尼;降阶方法

为了避免透平机械发生高周疲劳,叶片系统经常采用干摩擦阻尼结构来增加阻尼以减小叶片的振动幅值[1-2]。叶片振动过程中,干摩擦阻尼结构利用接触面之间振动产生的相互摩擦来消耗振动能量,降低振动水平。干摩擦阻尼结构的存在使叶片系统成为变刚度、变阻尼的非线性动力学系统。为了更好研究干摩擦阻尼结构叶片的振动特性,叶片系统常采用有限元模型进行分析。由于叶片系统的响应求解是一个非线性迭代过程,成圈叶片有限元模型自由度过多将导致迭代求解计算量非常大,直接求解难以实现。

本文综合波传动法、高阶谐波平衡法及Receptance法发展了一种计算围带成圈叶片非线性振动响应的高效求解方法,给出了该求解方法的详细推导过程。

1 求解方法

1.1 基于波传动法的围带成圈叶片降阶

当叶片静止时相邻叶片围带之间存在间隙,工作时叶片在离心力的作用下发生反向扭转变形,这种扭转变形使相邻叶片围带相互接触形成摩擦接触面。叶片振动时,围带接触面相互摩擦产生摩擦力消耗振动能量,减小振动幅值。当每只叶片受相同幅值、不同固定相位的气流激励时,相邻叶片各点的位移幅值相同且存在一个固定相位差。在该气流激励下采用波传动法,将具有循环对称特性的成圈叶片降阶成一个基本扇区的模型进行分析,相邻基本扇区之间的耦合力通过施加周期对称边界条件实现,可得整圈叶片的动力特性。

单个叶盘扇区有限元模型如图1所示,其有限元振动方程为

fb(qb(t))

(1)

图1 单个扇区的有限元模型

基本扇区的振动位移向量、摩擦力、周期对称面耦合力按左右摩擦接触面和周期界面自由度进行分块,即

(2)

(3)

(4)

式中:qml(t)、qmr(t)为左、右接触界面节点的位移;qbl(t)、qbr(t)为左、右周期对称面节点的振动位移;qo(t)为基本扇区其他节点的位移;fml(t)、fmr(t)为左、右接触面节点摩擦力;fbl(t)、fbr(t)为左、右周期对称界面的耦合力。

根据波传动法[7],左右周期对称界面上节点的振动位移和耦合力的关系为

qbr(t)=e-ihφI·qbl(t)

(5)

fbr(t)=-e-ihφI·fbl(t)

(6)

式中:I为单位矩阵;h为激励的阶数;φ=2π/N为相邻扇区之间的振动相位角;N为叶片数。

由式(5),可对基本扇区的振动位移q(t)进行缩减处理,即

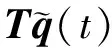
(7)

将式(7)代入式(1),并做变换,则基本扇区的振动方程变为

(8)

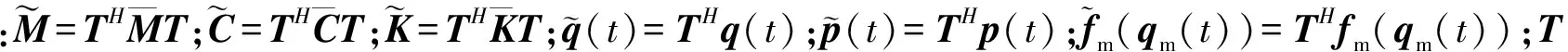
因此,通过波传动法施加周期边界条件,在变换过程中左周期对称界面上的自由度减小,且消去了未知周期对称界面上的耦合力。

根据周期对称结构的特点,对于第j、j+1个叶盘扇区,摩擦接触面上的振动位移关系为

qj+1(t)=qj(t+δt)=e-ihφqj(t)

(9)

第j个叶片左接触面和第j-1个叶片右接触面的相对位移及第j个叶片右接触面和第j+1个叶片左接触面的相对位移为

(10)

(11)

左右接触面上的相对位移存在关系

(12)

接触点对的非线性干摩擦力由相邻叶片接触面间的相对位移结合三维干摩擦微滑移模型[10]确定。同时,由于接触面振动位移是周期性的,故接触面的相对位移和干摩擦力也是周期性的。

1.2 振动响应的求解

谐波平衡法是求解非线性问题有效、快速的方法。叶片振动时接触面会有黏滞、滑移、分离的运动状态,分离时非线性项中的高次谐波对振动影响很大,对一次谐波平衡法的计算结果产生较大误差[2],因此本文采用高阶谐波平衡法求解振动方程。

当干摩擦阻尼叶盘系统受到周期性气流激励作用时,假设其振动响应与界面约束力均呈现周期性变化,可将叶盘系统的振动响应、气流激振力和干摩擦力展开成傅里叶级数

(13)

(14)

(15)

式中:h为谐波阶数;H为谐波平衡法中考虑的最大谐波数;ω为气流激振力的基频;Qh、Ph和Fmh分别为振动响应、激振力和接触面摩擦力的第h阶谐波的系数。

将式(13)～(15)代入式(8),可得非线性代数方程组

(16)

式(16)在频域内计算叶片的响应时,仅通过单个扇区的位移信息计算接触面的摩擦力,通过反复迭代计算得到系统的稳态响应。

尽管采用波传动法对成圈叶片进行了降阶,但由于叶片结构复杂,单只叶片有限元模型中通常有上万个节点,因此方程个数非常多,迭代求解很耗时,需要进一步降阶。本文将采用Receptance法做降阶处理,以便高效快速地求解叶片系统的非线性振动响应。Receptance法利用叶片正则振型的正交性对叶盘系统的振动方程进行解耦,然后利用叶盘系统接触界面非线性自由度远小于总体自由度的特性,只需要迭代求解叶盘系统接触界面上非线性自由度的振动响应,其余自由度上的振动响应可直接求解,从而可显著提高计算效率。

根据Receptance法,式(16)可写为

(17)

(18)

一般情况下,系统的前几阶振型对振动响应贡献较大,因此在计算过程中忽略系统的高阶振型,只考虑前几阶振型,式(18)可改写为

(19)

式中:M为计算过程振型的最高阶数。

(20)

(21)

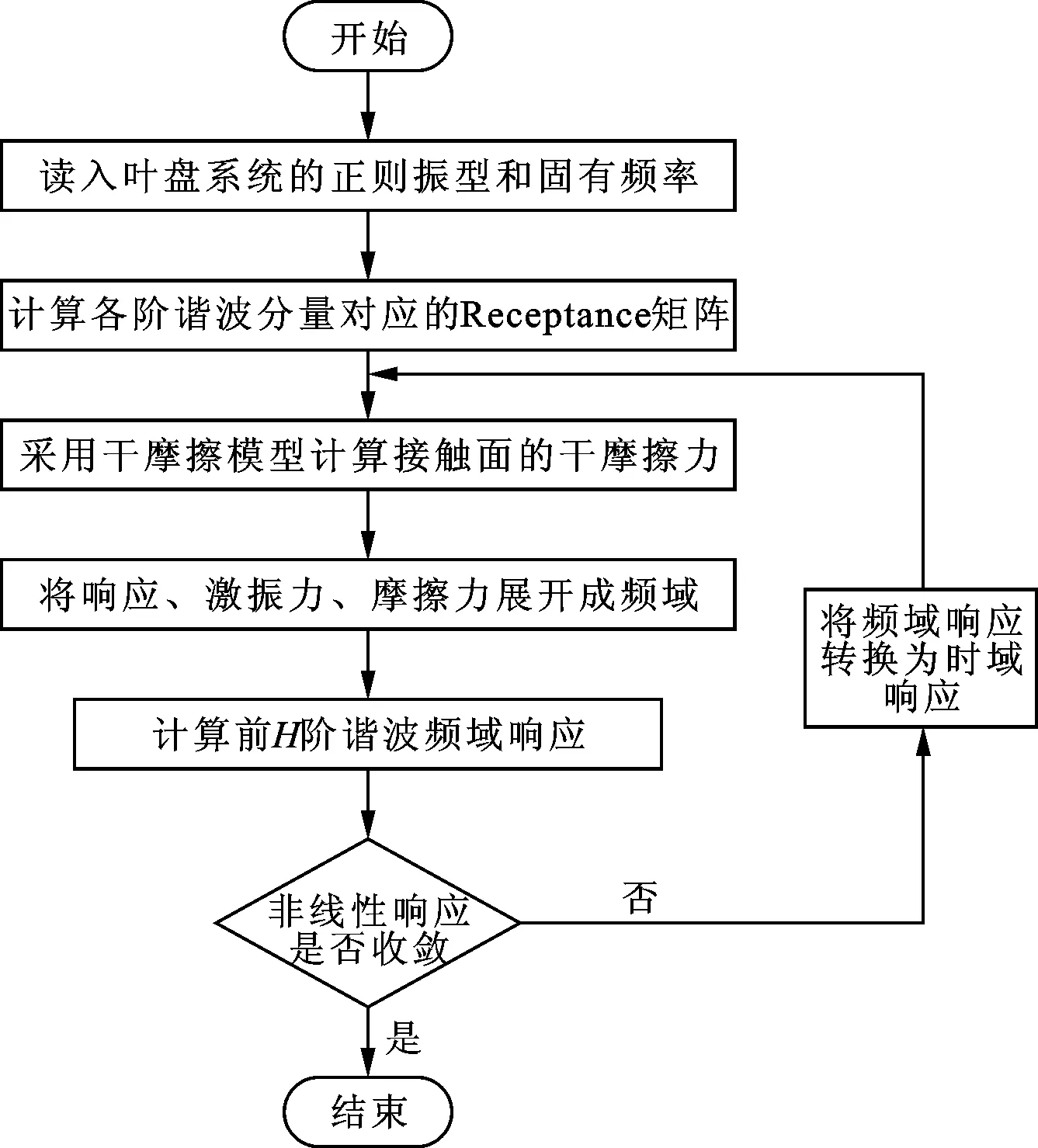
图2 计算摩擦接触面自由度振动响应的流程图

2 数值算例分析

2.1 计算方法的验证

为了验证本文方法的准确性和高效性,本文采用该降阶方法计算某简化围带成圈叶片的非线性振动响应,并与整体模型的直接计算结果进行比较。

简化的围带叶片扇区和成圈叶片整体结构的有限元模型如图3所示。叶片采用六面体八节点单元划分,成圈叶片由30个叶片组成,单个扇区包含3 240个节点,整体结构包含91 320个节点。材料参数为:密度ρ=7 800 kg/m3,弹性模量E=200 GPa,泊松比υ=0.3。

(a)单个扇区 (b)整体结构图3 简化的叶片模型

在叶片系统第一阶固有频率附近,取叶顶某一点的x、y、z方向的总位移,采用降阶方法和整体模型的计算结果如图4所示。

图4 降阶方法和直接计算结果

由图4可看出,采用降阶方法和整体模型计算得到的结果吻合得很好,最大相对误差位于共振点附近,直接计算的响应结果为0.607mm,降阶方法计算的结果为0.605mm,两者相差0.33%,计算时间仅为原来的10%。计算结果表明了本文降阶方法的正确性和高效性。

2.2 真实围带叶片分析

图5 真实围带叶片有限元模型

围带叶片在安装时存在一定的初始间隙,机组启动时,叶片在扭转恢复力的作用下初始间隙会逐渐减小,使围带之间形成摩擦接触面,并影响接触面的初始正压力,不同的初始间隙对应不同的初始正压力。本文计算中初始正压力的取值是根据扭转恢复后围带平均接触应力和平均接触面积计算得到的,本文通过计算围带叶片在不同初始正压力的振动响应,分析初始安装条件对围带叶片减振效果的影响,不同初始正压力下叶片系统的幅频响应曲线如图6所示。

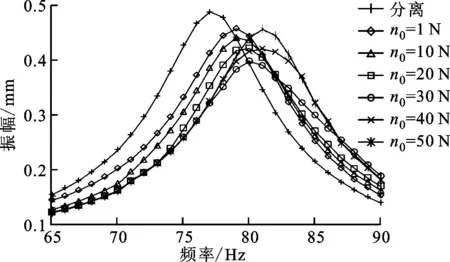
图6 不同初始正压力的幅频响应曲线

由图6可看出,围带叶片的响应没有出现多值、跳跃等典型的非线性特征,这是因为实际叶片设计时初始正压力比较大,在振动过程表现出的是弱非线性行为。共振幅值与初始正压力的关系和共振频率与初始正压力的关系如图7、8所示。

图7 共振幅值与初始正压力的关系

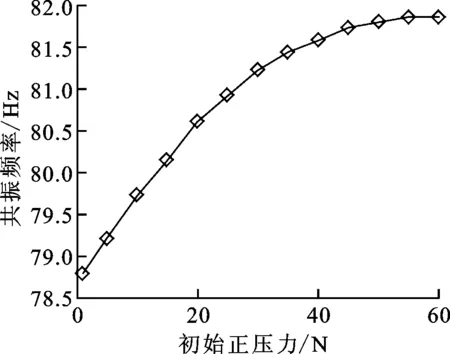
图8 共振频率与初始正压力的关系

由图7、8可看出,当接触面存在初始正压力时,随着初始正压力的增加,叶片共振峰值先减小后增大,最后趋于稳定,存在一个最优的初始正压力使叶片的共振幅值最小;共振频率随着正压力的增加而增加,最终趋于两接触面为接触刚度连接时叶片的固有频率。这是因为当围带接触面间的初始正压力较小时,围带间振动产生的摩擦力较小,此时摩擦力耗能小;随着初始正压力的增大,围带间的摩擦力逐渐增大,减振效果变好;当接触面初始正压力大到一定程度后,围带间难以产生相对运动,摩擦力耗能减小,减振效果变差。共振频率不断增大是因为初始正压力的增加使相邻围带间的相互约束逐渐变大。

3 结 论

本文综合波传动法、高阶谐波平衡法及Receptance法推导了一种计算围带成圈叶片的非线性振动响应的高效求解方法。该方法利用叶片系统的周期对称性,采用波传动法将成圈叶片降阶为一个基本扇区进行分析,使求解规模大幅度降低。该方法考虑了高次谐波的影响,能够求解复杂周期激励下叶片系统的非线性响应。通过叶片模态的正交性对叶盘系统的振动方程进行解耦,并利用叶片系统局部非线性的特点对非接触界面上的线性自由度进一步缩聚,从而减少了非线性迭代的规模,提高了计算效率。

采用本文求解方法得到的计算结果与采用整体模型的结果进行比较,结果验证了该方法的正确性与高效性。采用该方法预测了某真实围带叶片的振动响应,研究了初始正压力对围带叶片减振效果的影响,结果表明存在一个最优的初始正压力使叶片共振幅值最小,围带接触面间的初始正压力可通过调整叶片安装时的围带间隙来实现。

[1] 谷伟伟, 徐自力. 干摩擦阻尼叶片的界面约束力描述及振动响应求解 [J]. 振动工程学报, 2012, 25(1): 64-67. GU Weiwei, XU Zili. Description of constraint force for dry friction and prediction of vibration responses on damped blade [J]. Journal of Vibration Engineering, 2012, 25(1): 64-67.

[2] 史亚杰, 单颖春, 朱梓根. 带凸肩叶片非线性振动响应分析 [J]. 航空动力学报, 2009, 24(5): 1158-1165. SHI Yajie, SHAN Yingchun, ZHU Zigen. Analysis of nonlinear response of shrouded blades system [J]. Journal of Aerospace Power, 2009, 24(5): 1158-1165.

[3] PANNING L, SEXTRO W, POPP K. Optimization of the contact geometry between turbine blades and underplatform dampers with respect to friction damping [C] ∥Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air. New York, USA: ASME, 2002: 991-1007.

[4] KURAN B, ÖZGÜVEN H N. A modal superposition method for non-linear structures [J]. Journal of Sound and Vibration, 1996, 189(3): 315-339.

[6] PETROV E P. A method for use of cyclic symmetry properties in analysis of nonlinear multiharmonic vibrations of bladed disks [J]. ASME Journal of Turbomachinery, 2004, 126(1): 175-183.

[7] THOMAS D L. Dynamics of rotationally periodic structures [J]. International Journal for Numerical Methods in Engineering, 1979, 14(1): 81-102.

[8] 谢永慧, 张荻. 汽轮机阻尼围带长叶片振动特性研究 [J]. 中国电机工程学报, 2005, 25(18): 96-90. XIE Yonghui, ZHANG Di. Numerical model for vibration characteristic of steam turbine blade with damped shroud [J]. Proceedings of the CSEE, 2005, 25(18): 96-90.

[9] 秦飞, 张晓峰, 白洁, 等. 循环对称结构动应力计算的一种工程处理方法 [J]. 北京工业大学学报, 2006, 32(s1): 64-67. QIN Fei, ZHANG Xiaofeng, BAI Jie, et al. A new approach of dynamic stress analysis for cyclic symmetry structures [J]. Journal of Beijing University of Technology, 2006, 32(s1): 64-67.

[10]GU W W, XU Z L. 3D numerical friction contact model and its application on nonlinear vibration of damping blade [C] ∥Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air. New York, USA: ASME, 2010: 809-817.

(编辑 赵炜 苗凌)

An Efficient Method for Solving Vibration Response of Continuous Covered Blades with Damped Shroud

QIU Hengbin,XU Zili,LIU Yalin,SHANG GUAN Bo

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China; 2. Institute of Environmental and Municipal Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China; 3. Xi’an Thermal Power Research Institute Co. Ltd., Xi’an 710032, China)

An efficient solution method based on wave propagation method, multi-harmonic balance method and Receptance method was developed to solve the problem with overlarge degrees of freedom and computational complexity in calculating the nonlinear vibration response of continuous covered blades with damped shroud. According to the cyclic symmetry property of blade, the vibration analysis of a whole blade can be reduced to one of its basic sector using wave propagation method and the nonlinear friction force can be solved from the displacement of the basic sector and friction contact model; the differential equations in time domain of the reduced basic sector can be transformed into algebraic equations in frequency domain by multi-harmonic balance method. The orthogonality of normalized modes is used to decouple the vibration equation of blade in frequency domain and the local nonlinear characteristics of the blade system are used to condense the linear DOFs in non-contact interfaces. So that the scale of nonlinear iteration can be effectively reduced and the computation efficiency is improved. The results showed that the relative error obtained with the developed method was 0.33% and the calculation time was reduced to 10%, which verifies the accuracy and efficiency of the proposed method. The nonlinear vibration response of a real shrouded blade was investigated by this method.

whole blade; vibration response; shroud damper; order-reducing method

2016-04-07。 作者简介:邱恒斌(1991—),男,硕士生;徐自力(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51275385)。

时间:2016-09-14

10.7652/xjtuxb201611001

TK263.3

A

0253-987X(2016)11-0001-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160914.1805.008.html