粗糙表面确定性接触模型中峰的再定义

王庆朋,张力,杜宝程,郑仁蔚

(重庆大学汽车工程学院,400044,重庆)



粗糙表面确定性接触模型中峰的再定义

王庆朋,张力,杜宝程,郑仁蔚

(重庆大学汽车工程学院,400044,重庆)

为了解决目前不同微凸峰确定准则所等效的接触模型中可能存在峰的不连续、重叠、丢失而造成接触过程中缺失基准,从而导致粗糙表面在相互作用过程中不能进行有效计算等问题,在3点峰和3点谷的基础上,定义当3个连续峰的中间峰高于相邻峰时为真峰、当3个连续谷的中间谷低于相邻谷时为真谷,并对其进行匹配得到“谷-峰-谷”模式的微凸峰。通过一组粗糙表面,分析了不同的采样间隔和粗糙度对峰数量、平均峰半径和峰高度的影响,并与文献中不同的准则进行了对比。结果表明:不同微凸峰确定准则所等效的模型具有很大的不确定性;随着采样间隔的增加,峰数量明显减少,平均峰半径和峰高度增大,当采样间隔小于0.5 μm时,不同的确定准则影响减小;随着粗糙度的降低,峰数量略微增多,平均峰半径增大,平均峰高度减小。该模式的微凸峰为接触特性的演化提供了一个基准。

粗糙表面;微凸峰;确定准则;峰半径

在机械系统中,界面处的表面形貌对系统的动态特性、摩擦学性能、表面完整性以及装配可靠性等都有着至关重要的影响。目前,研究粗糙表面接触模型的方法主要有概率统计、分形理论、数值计算和确定性理论等。Greenwood等将粗糙表面视为一系列等半径且高度服从高斯分布的球体,提出了经典的粗糙表面与平板之间的接触模型[1],这一理论得到了广泛的应用,但是该学者也意识到等半径建模方法的不足[2]。Nayak采用功率谱密度函数对随机表面进行表征[3],该方法需要设计合理的滤波器,缺乏通用性。Majumdar等首先基于W-M分形函数建立了M-B弹塑性接触模型[4],由于分形参数的尺度独立性,这一方法也有了很大的发展,但是该方法只适用于具有分形特征的工程表面。文献[5-6]采用有限元的方法对粗糙表面进行弹塑性分析,该方法可以最大程度地逼近真实接触情况,Persson对此指出,如果对一粗糙表面考虑到纳米尺度,可能包括约7个数量级,对应1021个自由度,这样进行数值计算显然是不现实的[7]。对真实粗糙表面上的微凸体进行简化是必要的,在已有文献中常见的有:球[1]、椭球[2]、圆柱[8]、锥[9]和正弦曲线[9]等一些简单的形状,由于球状微凸体的理论分析和实验研究相比其他形状更容易实现,因此被更多的学者所采用。对于二维粗糙表面轮廓的确定性接触模型,Greenwood提出了3点峰准则(3PP)[10],利用中间点高于相邻两点的3点构建一个圆,类似地,Tomanik提出5点峰准则(5PP)[11],Poganik等提出7点峰准则(7PP)[12]。Poon等在3点峰的基础上,增加了峰点与相邻两点高度差必须大于设定值这一条件(M3PP)[13],Ghosh等基于刚性平面和轮廓的两个交点以及这两点之间的最大值,提出可变半径3点峰准则(VR3PP)[9]。以上5个准则均是首先确定轮廓上的3个点,然后利用三角形外接圆确定半径和圆心位置。Bigerelle等提出的准则和文献[9]类似,只是半径的计算方法不同[14]。

随着测量仪器分辨率的逐步提高,粗糙表面的测量面临着一个问题,即所测量的参数是用一个有限的值来近似一个无限的值[2],换言之,当采样间隔趋于无限小,微凸峰的数量将趋于无限多,峰半径和接触面积将趋于无穷小,接触压力将趋于无穷大。由此可见,目前粗糙表面确定性接触模型中峰的信息具有很大的不确定性。此外,以上准则所确定的模型中可能存在峰的不连续、重叠、丢失而导致接触过程中缺失基准等问题。鉴于此,本文对粗糙表面上的微凸峰进行重新定义,得到“谷-峰-谷”模式的微凸峰,并且与文献中不同的准则进行了对比,从而验证了本文所建准则的有效性。

1 确定性接触模型

1.1 微凸峰的确定准则

表面几何特征使界面的研究,包括机械、热、物理或化学等,能够更深入地探索微观本质。在确定性接触模型中就是如何定义微凸峰的数量、大小和位置。在一定采样长度和采样间隔情况下的微凸峰确定准则[9-13]如表1所示。

通过表1可以看出,对于粗糙表面轮廓,由不同的采样间隔和峰高度可以得到不同的微凸峰信息,尤其在极限情况下,可以得到无穷多个半径为无穷小的微凸峰,这显然不符合实际接触。为了更合理、有效地确定微凸峰,本文借鉴了地貌的概念。所谓山峰或山谷,是因为其高于或低于四周,实际中并没有将山峰上的某块石头或山腰上的侧峰称为山峰(更严格地说,应该为主峰),山谷类似。山峰和山谷对应,即一峰对两谷。工程粗糙表面轮廓和地貌特征只是尺度上的差别。任何简化的微凸峰其实都包含着许多更小尺度的微凸峰,而针对这一问题,作者对单个微凸峰的接触特性进行了分析,并且提出混合弹塑性接触模型[15]。

表1 微凸峰的确定准则[9-13]

注:m为轮廓中线;zi为i点轮廓高度;Δzi为相邻两点之间的高度差;vset为准则中的设定值。

1.2 计算流程

对于二维粗糙表面轮廓,主要的计算步骤如下:

(1)利用中间点高于相邻两点的3点确定轮廓上的一个峰,利用中间点低于相邻两点的3点确定轮廓上的一个谷;

(2)在步骤(1)的基础上,利用“峰上峰”再求一峰,“谷下谷”再求一谷;

(3)对步骤(2)的结果进行匹配,并且要求中间峰高度必须大于相邻两谷,从而实现“谷-峰-谷”模式的微凸峰。

在计算过程中,相邻微凸峰共用一个谷,这样就可以确保等效表面的连续性,避免重叠。计算流程如图1所示,等效粗糙峰的示意图如图2所示。

图1 确定性接触模型中粗糙峰的计算流程

图2 确定性接触模型中等效粗糙峰的示意图

1.3 粗糙表面轮廓

目前,对于粗糙表面轮廓数据点的获得主要通过实验测量和计算机仿真,由于本文意在验证所建粗糙峰的确定准则,不失一般性,采用分形理论获得一组二维表面轮廓,当采样长度为800 μm、采样间隔为0.5 μm时的粗糙度算术平均偏差Ra和均方根偏差Rq如表2所示,其中轮廓4及其等效模型如图3所示。从图中可以看出,轮廓上主要的峰和谷被提取了出来,而谷又是相邻圆的交点,这克服了3PP、5PP、7PP和VR3PP准则结果中出现的等效峰不连续、重叠和丢失等现象,并为压缩过程中面积或体积演变提供了一个基准。

表2 表面轮廓的粗糙度

图3 粗糙表面轮廓4及其等效峰

2 不同准则结果的比较

为了对不同准则的结果进行比较,采用了采样长度和高度2种对比方案:①同一表面轮廓不同的采样间隔;②同一采样间隔不同的表面轮廓。由于M3PP准则中设定值有不同的取值,根据文献[12-13]的对比结果,本文选取了5%Rq和10%Rq;在VR3PP准则中刚性平面有不同的位置高度,本文取0 μm和Rq。

2.1 不同采样间隔的影响

为了分析不同采样间隔对微凸峰数量、平均峰半径和峰高度的影响,采用表面轮廓4,采样间隔分别为0.05、0.1、0.3 μm和在0.5～5 μm之间每隔0.5 μm进行一次取值。

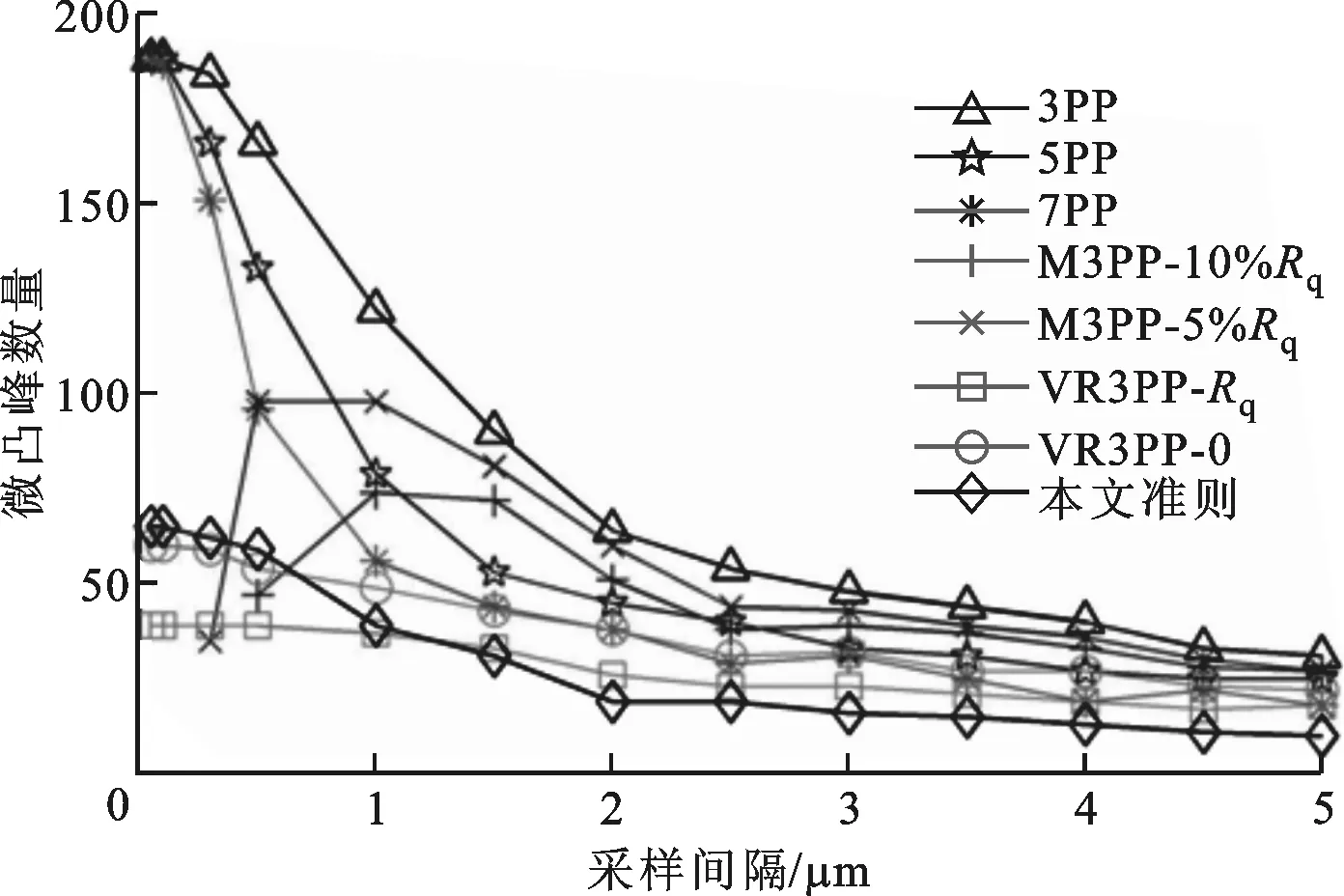
(a)采样间隔对微凸峰数量的影响

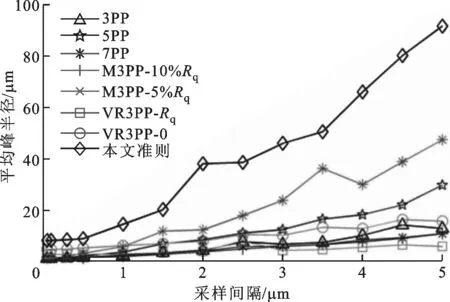
(b)采样间隔对平均峰半径的影响

(c)采样间隔对平均峰高度的影响图4 采样间隔对不同准则等效峰结果的影响

2.1.1 微凸峰数量 对于不同的微凸峰确定准则,峰数量、平均峰半径和峰高度随采样间隔的变化如图4所示。从图4a中可以看出,峰数量随着采样间隔的增加而减小,这就如同在一定区域内等效球体、晶胞和原子数目的变化规律一样。图中变化最为明显的是3PP、5PP和7PP准则计算的结果,从采样间隔0.05 μm的约190个峰降低到采样间隔5 μm的30个左右。VR3PP准则中高度为Rq和0 μm的两个结果以及本文准则对应的结果变化较为平缓,本文准则对应的结果从开始的65个峰减少到最后的10个。M3PP准则中5%Rq和10%Rq的两个结果在采样间隔大于1.5 μm时的变化趋势与其他准则的结果类似,但是在采样间隔小于1.5 μm时的结果开始变小,如果再小就不能确定微凸峰信息。

2.1.2 平均峰半径 微凸峰平均半径的变化规律如图4b所示,其变化趋势和峰数量的变化正好相反。从物理角度来看,基元的尺度减小,其数量肯定增加,原来表现为接触的,可能因为尺度的减小而发生分离,相应的接触面积必然减小,在同等受力条件下接触压力将变大,这与工程中细化晶粒的结果是一致的,即所谓的“越小越强”。在采样间隔为0.05 μm时,除了M3PP准则不能计算之外,其他准则的结果均在10 μm以内,3PP准则的结果最小,为0.47 μm,从小到大依次为5PP、7PP和VR3PP准则所确定的结果,本文准则确定的平均峰半径最大,为7.54 μm。在采样间隔为5 μm时,不同准则之间差别变大,最为明显的是5PP、7PP和本文准则所确定的结果,其他准则均在20 μm以下。

2.1.3 平均峰高度 微凸峰平均高度的变化规律如图4c所示。从整体变化趋势来看,平均峰高度随着采样间隔的增加而变大,这可以理解为,减小间隔使原来更小尺度、相对较低的微凸峰成为新的等效峰。3PP、5PP和M3PP准则确定的峰高度在1.5～2.5 μm之间变化,7PP和VR3PP准则的0 μm位置的结果变化范围更大一些,本文准则确定的结果变化最为明显,而VR3PP准则Rq位置的结果变化较为平缓。

2.2 不同粗糙度的影响

为了分析不同粗糙度对微凸峰数量、平均峰半径和峰高度的影响,采用采样间隔为0.5 μm对7个表面轮廓进行分析。

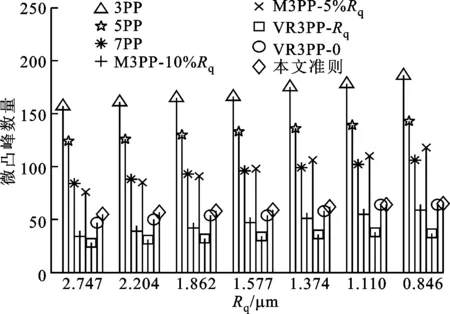
(a)粗糙度对微凸峰数量的影响

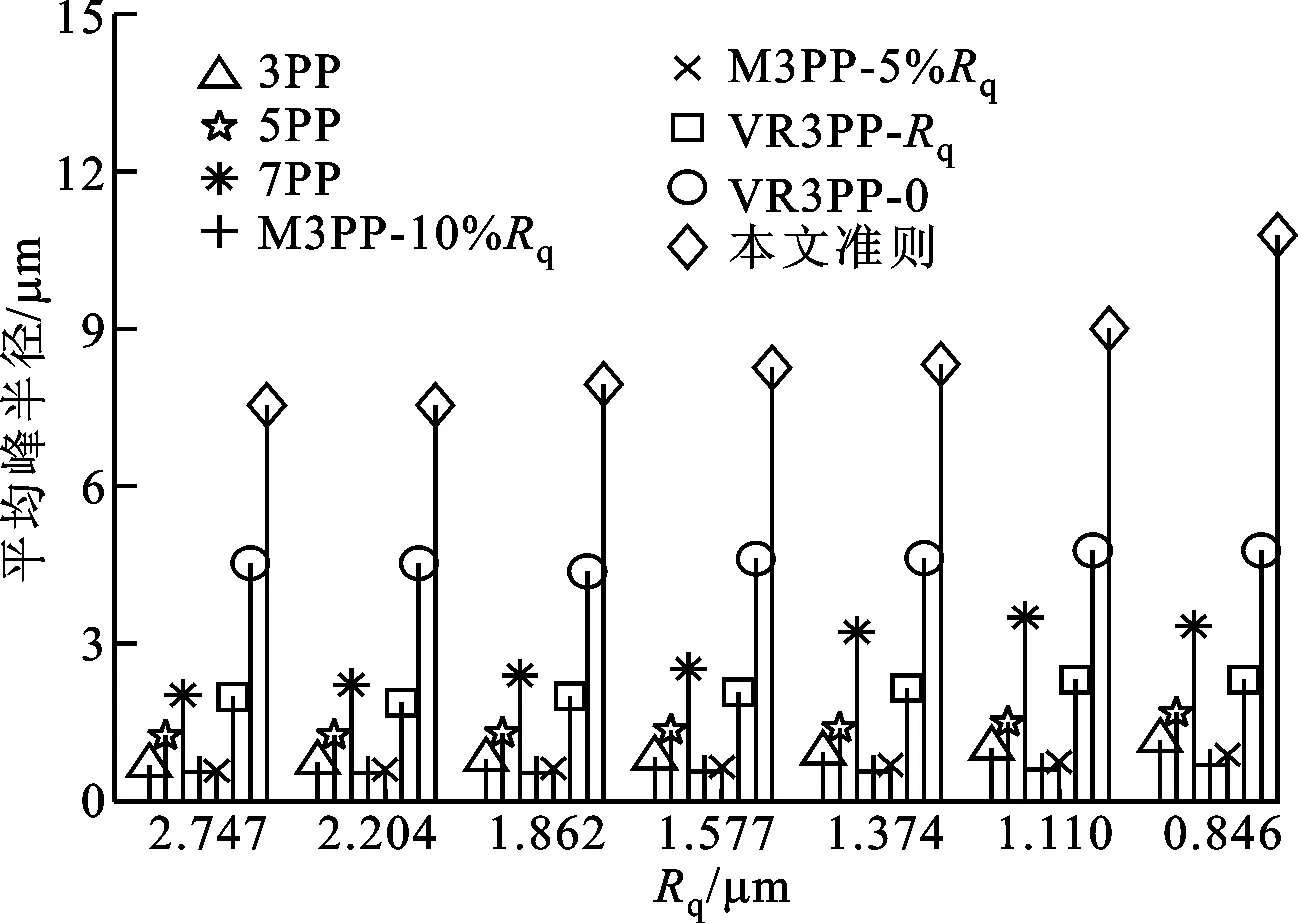
(b)粗糙度对平均峰半径的影响

(c)粗糙度对平均峰高度的影响图5 粗糙度对不同准则微凸峰结果的影响

2.2.1 微凸峰数量 微凸峰数量、平均峰半径和峰高度随着粗糙度的变化如图5所示。从图5a中可以看出,对于不同的微凸峰确定准则,均表现为峰数量随着粗糙度的降低而增多。这是因为粗糙度的降低使表面轮廓变得平整,也就会有更多的点符合峰的确定准则。3PP准则对应的微凸峰数量最多,从Ra为2.747 μm时的157个变为Ra为0.846 μm时的186个;3PP、5PP、7PP和VR3PP对应结果的增长率近乎相同;M3PP由于对3PP准则增加了限制条件,所以数量要小于3PP、5PP的结果,但增长率表现为最大,同时条件中设定值的增加使数量减小,5%Rq的结果几乎是10%Rq的两倍;本文准则的数量增长率最小,从开始的55个增加到65个。

2.2.2 平均峰半径 从图5b可以看出,平均峰半径随着粗糙度的降低而变大,本文和7PP准则对应的结果变化最为明显,其他准则的结果几乎不变,同时本文准则确定的峰半径比其他准则的大。除了7PP、VR3PP的0 μm位置和本文准则峰半径计算的结果大于2 μm以外,其他的均小于2 μm。对于M3PP准则,当采样间隔小于0.3 μm时不能确定相应的微凸峰信息。

2.2.3 平均峰高度 从图5c可以看出,平均峰高度的变化趋势和峰数量、平均峰半径的相反,对于不同准则所对应的平均峰高度随着粗糙度的降低而降低,其变化范围为从开始的3 μm左右降低到1 μm左右,除了VR3PP准则Rq位置的结果,其他准则对应的结果呈现出几乎一致的趋势,可见在同一采样间隔下的微凸峰高度受不同准则的影响很小。

3 结 论

目前,不同微凸峰确定准则所等效的接触模型中可能存在峰的不连续、重叠、丢失而导致接触过程中缺失基准,不能合理地分析接触面积或接触力等的演化规律。本文对粗糙表面上的微凸峰进行了重新定义,最终实现“谷-峰-谷”模式的微凸峰,该准则能够提取表面轮廓中主要的峰和谷,并且使等效模型的表面轮廓连续,从而为接触过程中材料守恒提供了一个基准。通过一组粗糙表面轮廓与文献中不同的准则进行对比,验证了本文准则的有效性。

通过对比分析知,不同微凸峰确定准则所等效的模型具有很大的不确定性。随着采样间隔的增加,微凸峰数量随之减少,平均峰半径和峰高度增大,当采样间隔小于0.5 μm时,确定准则的影响减小;随着粗糙度的降低,微凸峰数量随之增多,平均峰半径变大,而平均峰高度减小。

[1] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London, 1966, 295: 300-319.

[2] GREENWOOD J A. A simplified elliptic model of rough surface contact [J]. Wear, 2006, 261(2): 191-200.

[3] NAYAK P R. Random process model of rough surfaces [J]. Journal of Lubrication Technology, 1971, 93(3): 398-407.

[4] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. Journal of Tribology, 1991, 113(1): 1-11.

[5] BRIZMER V, ZAIT Y, KLIGERMAN Y, et al. The effect of contact conditions and material properties on elastic-plastic spherical contact [J]. International Journal of Solids and Structures, 2006, 43(18): 5736-5749.

[6] 赵波, 戴旭东, 张执南, 等. 单峰接触研究及其在分形表面接触中的应用 [J]. 摩擦学学报, 2014, 34(2): 217-224. ZHAO Bo, DAI Xudong, ZHANG Zhinan, et al. Single asperity contact and its use for fractal surface contact [J]. Tribology, 2014, 34(2): 217-224.

[7] PERSSON B N J. Contact mechanics for randomly rough surfaces: on the validity of the method of reduction of dimensionality [J]. Tribology Letters, 2015, 58(1): 1-4.

[8] 田红亮, 陈甜敏, 郑金华, 等. 平行轴圆柱副接触分析 [J]. 西安交通大学学报, 2016, 50(1): 8-15. TIAN Hongliang, CHEN Tianmin, ZHENG Jinhua, et al. Contact analysis of cylindrical pair with parallel axes [J]. Journal of Xi’an Jiaotong University, 2016, 50(1): 8-15.

[9] GHOSH A, SADEGHI F. A novel approach to model effects of surface roughness parameters on wear [J]. Wear, 2015, 338/339: 73-94.

[10]GREENWOOD J A. A unified theory of surface roughness [J]. Proceedings of the Royal Society of London, 1984, 393: 133-157.

[11]TOMANIK E. Modeling of the asperity contact area on actual 3D surfaces: SAE 2005-01-1864 [R]. Washington, DC, USA: SAE, 2005.

[13]POON C Y, BHUSHAN B. Surface roughness analysis of glass-ceramic substrates and finished magnetic disks, and Ni-P coated AlMg and glass substrates [J]. Wear, 1995, 190(1): 89-109.

[14]BIGERELLE M, NIANGA J M, NAJJAR D, et al. Roughness signature of tribological contact calculated by a new method of peaks curvature radius estimation on fractal surfaces [J]. Tribology International, 2013, 65(3): 235-247.

[15]王庆朋, 张力, 尚会超, 等. 考虑应变硬化的混合弹塑性接触模型 [J]. 西安交通大学学报, 2016, 50(2): 132-137. WANG Qingpeng, ZHANG Li, SHANG Huichao, et al. Mixed elastic-plastic contact model considering strain hardening [J]. Journal of Xi’an Jiaotong University, 2016, 50(2): 132-137.

(编辑 苗凌)

Re-Definition of Asperity-Peak for Deterministic Contact Model on Rough Surfaces

WANG Qingpeng,ZHANG Li,DU Baocheng,ZHENG Renwei

(College of Automotive Engineering, Chongqing University, Chongqing 400044, China)

No baseline exists to evaluate the contact characteristics for deterministic contact model owing to the discontinuity, overlapping and missing of the asperity-peak. Based on the criteria of 3-point peak and 3-point valley, the middle higher peak or lower valley can be firstly identified as the true one in the three continuous peaks or valleys, and then a new asperity-peak of “valley-peak-valley” mode is defined. The proposed criterion is validated through a set of different surface profiles, and compared with other criteria found in the literature. The results show the huge influence obtained after using these different criteria. The number of asperity peaks decreases obviously with the increasing sampling interval, however, the mean asperity-peak radii and heights increase. The effects of different criteria on the calculated asperity-peak properties become almost negligible when the sampling interval is below 0.5 μm. The number of asperity peaks increases slightly with the decreasing surface roughness, and a similar tendency is found for the mean radii while the mean heights have an opposite effect. This criterion can provide a baseline for the evolution of the contact characteristics.

rough surface; asperity peak; identification criteria; asperity-peak radius

2016-03-01。 作者简介:王庆朋(1987—),男,博士生;张力(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51175530)。

时间:2016-09-08

10.7652/xjtuxb201611018

O343.3

A

0253-987X(2016)11-0115-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160908.1104.012.html