气动弹性系统本征正交分解降阶模型精度的参数影响研究

张鸿志,周强,陈刚,李跃明

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049,西安)



气动弹性系统本征正交分解降阶模型精度的参数影响研究

张鸿志1,2,周强1,2,陈刚1,2,李跃明1,2

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049,西安)

为了快速分析跨音速非线性气弹系统的颤振边界和响应特性,通过本征正交分解(POD)降阶方法建立了基于CFD的气动弹性降阶模型(ROM)。实现过程包括对非线性定常CFD流场的小扰动泰勒分解,建立基于CFD的全阶线性化模型;再通过POD方法得到流体ROM;耦合结构动力学方程构成基于CFD的气弹ROM。以国际气弹标模AGARD 445.6机翼为研究对象,系统研究了ROM建立过程中初始流场、响应时间步长和样本数据等重要参数对于模型精度的影响,并将ROM应用于颤振边界的预测。研究表明:作为线性化方程建立的定常流场,若收敛性不够,易导致线性化模型不稳定甚至发散;响应计算中,时间步长若选取过大将会导致数值振荡、发散;为捕捉更多的非线性流场特性,系统激励后POD样本的产生需保证足够的数据采集时间;所建立的ROM具有同原始非线性CFD/CSD系统同样的精度,是一个低维度状态空间数学模型,可直接用于系统特性分析和颤振抑制等设计。相比CFD/CSD耦合计算,ROM在计算效率上提高了3～6个量级。

CFD/CSD耦合;降阶模型;本征正交分解;颤振

飞行器气动弹性研究飞行器结构与气动力相互耦合关系,是典型的流固耦合振动问题。在空气跨声速流动阶段,由于流体的可压缩性导致激波运动、涡脱落等强非线性效应,升力面法、偶极子法等传统线性化方法很难处理跨声速阶段流体非线性气动力。目前,基于CFD/CSD耦合计算飞行器的气动弹性可很好捕捉该阶段流体非线性特性,广泛应用于低速、跨声速和超声速等非线性流固耦合分析中[1-2],但CFD/CSD耦合计算时间耗费巨大,特别是对于需要反复迭代修改的多学科优化初步设计阶段,从而限制了其广泛应用[3]。近年来,基于CFD的线性、非线性气动弹性模型降阶[4-5](ROM)有效克服了这一问题。ROM的主要目的是建立一个低维的数学模型,能很好体现原始系统动力学特性,可直接应用于气动弹性快速分析、气动弹性主动控制[6-7]、颤振优化等工程设计中。

本征正交分解(POD)降阶[8-9]是目前应用比较广泛的降阶方法之一,其原理是寻找系统动力学特性的最优特征模态[10-11],POD方法需建立在流体内部流场上,能保留流场中激波等非线性特性,更能反映流体的内部结构特征,所以初始流场的计算精度、响应计算的时间步长、样本数据等参数的选取对计算结果有很大影响。基于CFD的气动弹性POD降阶构造,尤其对于面向复杂模型的POD降阶求解器精度的影响因素,文献[8]详细研究了基于CFD的气动弹性POD/ROM建模,分析了部分参数对结果精度的影响,该研究主要通过频域方法产生POD样本数据构建ROM系统。但是,频域方法建立的ROM并不能包含完整流场非线性特性,而本文研究的时域POD/ROM具有更强的鲁棒性,能捕捉更多流场信息,为构造高质量ROM提供指导性原则和建议。

1 数值理论基础

1.1 非线性气动弹性控制方程

基于CFD/CSD耦合求解气动弹性方法是求解流体、结构动力学方程,通过交界面的数据交换,反复耦合计算实现的。气动弹性系统控制方程为

(1)

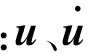
本文所采用的CFD求解器为结构化网格求解器,离散格式采用Vanleer格式,时间推进为隐式LU-SGS格式。结构动力学求解采用模态叠加法,流体固体之间的数据传递采用基于IPS的插值方法,动网格采用基于RBF的TFI动网格方法[12]。在CFD求解中的网格数一般为105～107量级,求解流体动力学方程需通过反复迭代求解得到,占据整个气弹求解99%以上的计算时间和资源,CFD/CSD耦合求解通常需要十几小时甚至数天。

1.2 气动弹性系统线性化方法

对于颤振这类小扰动问题,式(1)是一个强非线性隐式方程,为了得到其显式表达式,对式(1)进行线性化求解。对于气动弹性系统,选取结构未变形的定常状态流场作为初始流场,即

(2)

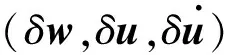
(3)

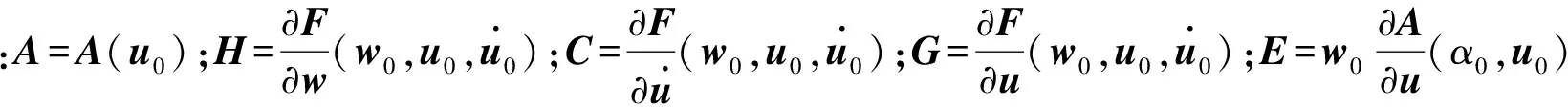
1.3 POD降阶方法

POD降阶方法是通过选择一组试验数据样本集来构造降阶过程中所需的变换矩阵来得到降阶系统。一系列样本数据{xk},xk∈Rn为n维向量,m个n维样本数据构成一个大型矩阵,POD方法就是寻找一个最优化的基底向量Ψr=(Ψ1,Ψ2,…,Ψr),r≪n,使得投影到该基底子空间的降阶系统能很好地保持原系统的动力学特性,向量为

(4)

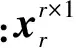
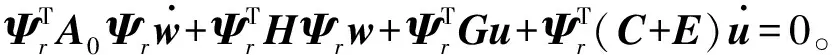
2 基于CFD/CSD的气动弹性求解器

本文的POD/ROM方法是基于CFD/CSD求解器基础上发展而来的,计算采用国际上用于检验颤振计算方法的AGARD445.6机翼标准模型,由于CFD/CSD求解器对于该模型的验证已在文献[12]中详细讨论,本文主要分析耦合求解中网格数量的影响。

CFD的求解与网格的数量有密切关系,网格数越多,求解精度越高,但是计算量会成倍增加。本文建立了3套数量不同的流体网格,网格分布如图1所示。

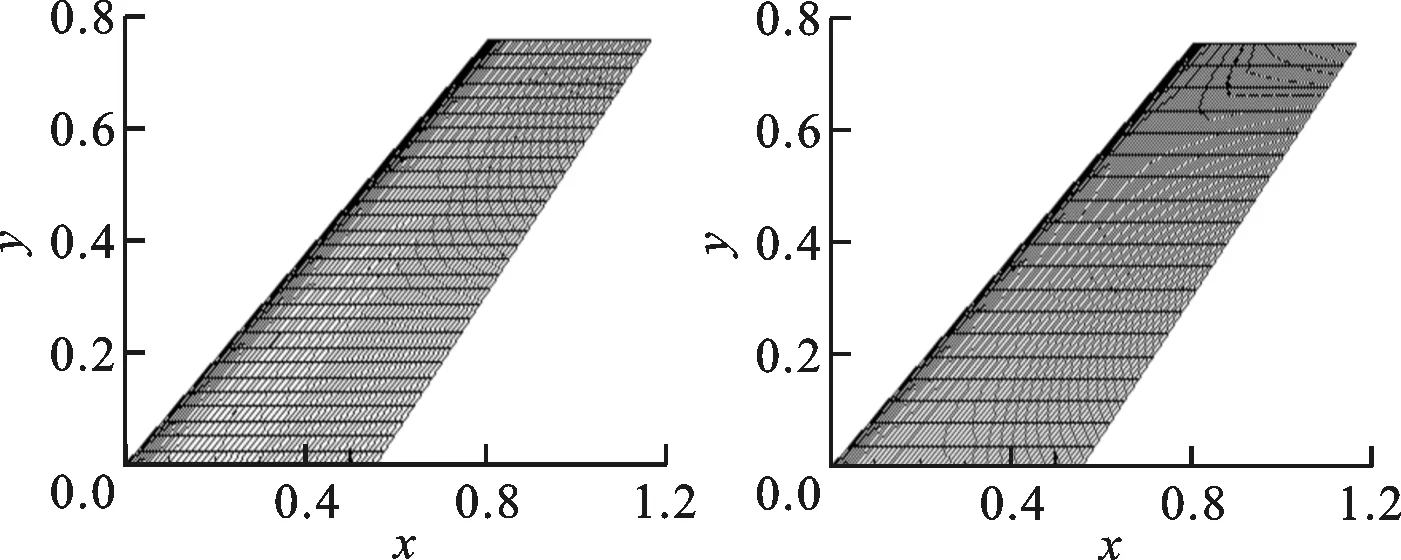
(a)网格数为10万 (b)网格数为20万

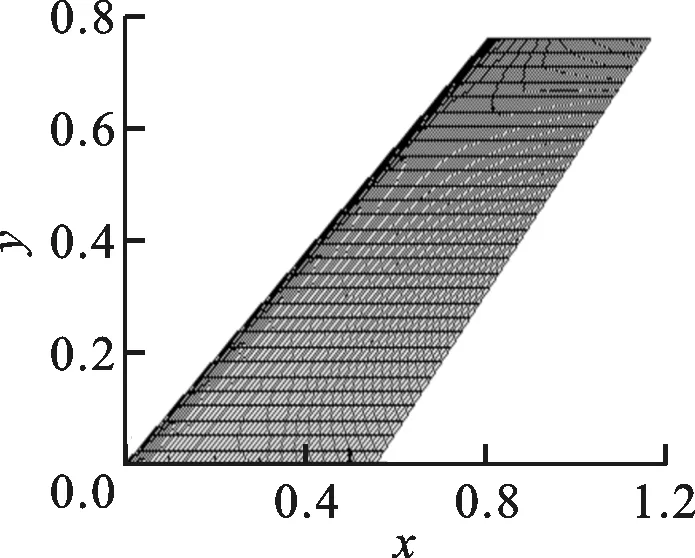
(c)网格数为30万图1 不同网格模型机翼表面流体网格分布

计算马赫数为0.901、来流迎角为0°、速度V为310 m/s、密度ρ为0.099 5 kg/m3状态下的气弹响应,迭代时间步长Δt为0.000 1 s,每时间步迭代次数为50,不同网格数量下的升力系数CL、力矩系数CM随时间的响应如图2所示。本文的结构求解基于模态叠加法,不同流体网格的第1阶广义模态位移响应比较如图3所示,广义模态力和广义模态位移均为无量纲表示。网格数为20万和30万响应结果的幅值、频率、趋势基本相同,而网格数为10万的响应精度不够,考虑到精度和效率的关系,本文选取网格数为20万的模型作为构建ROM的基准网格。

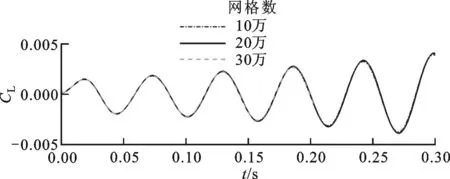
(a)升力系数

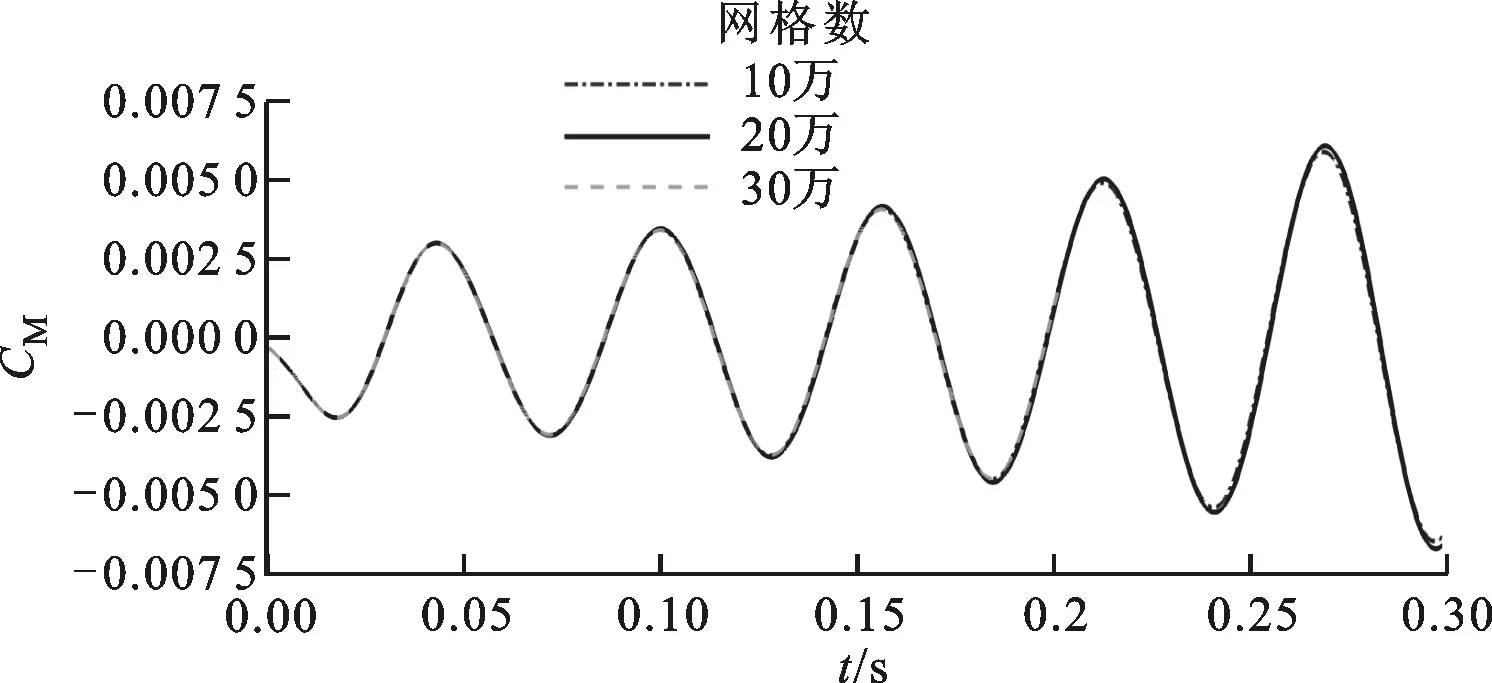
(b)力矩系数图2 不同网格响应比较

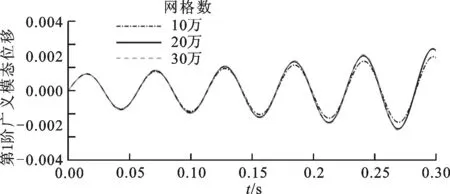
图3 不同流体网格的第1阶广义模态位移响应比较

3 降阶模型精度的参数影响分析

ROM是在CFD流场下的线性化小扰动模型基础上得到的,不同的初始条件对降阶结果的精度影响很大,本文主要讨论影响降阶结果的重要参数,流体网格选用网格数为20万、全阶自由度约为100万的网格。

3.1 定常流场收敛性对线性化模型的影响

为了考察初始流场的影响,选取跨音速状态下、马赫数为0.901、来流迎角为0°、采用不同迭代次数的初始流场建立全阶线性化模型,选取第1阶广义模态位移运动形式为ξ1=0.001sin(2π55.3t)的强制位移,不同流场下的线性化非定常气动力如图4所示。由图4可看出,开始的响应非常接近,且都很光滑,但计算几个周期后,建立在定常迭代计算5 000步流场下的线性化模型出现了数值发散,而建立在迭代10 000步后的线性化模型很好地保持着数值稳定。由此可知,定常流场的收敛性对线性结果影响很大。

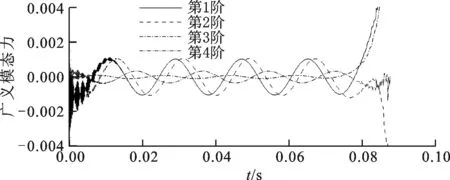
(a)定常计算迭代5 000步

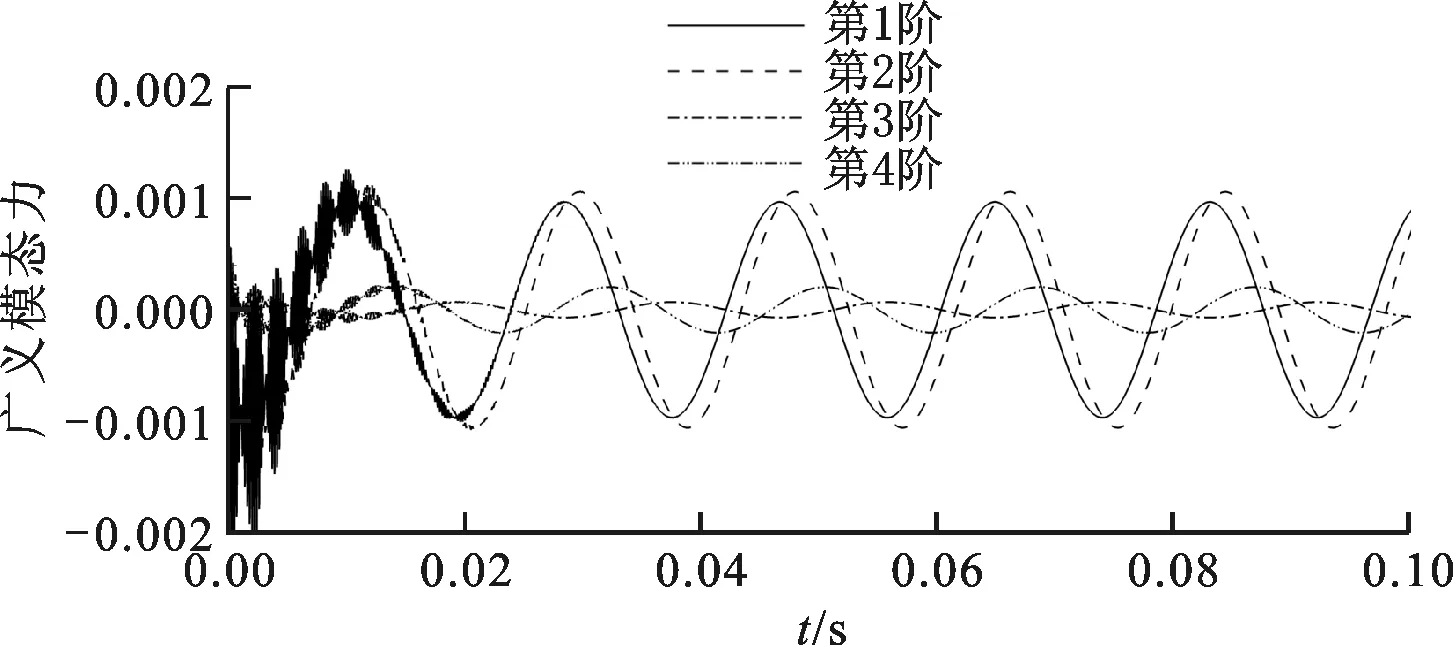
(b)定常计算迭代10 000步图4 不同流场下的线性化非定常气动力

3.2 时间步长对线性化计算的影响

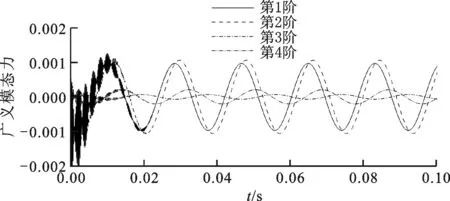
(a)Δt=1×10-4 s

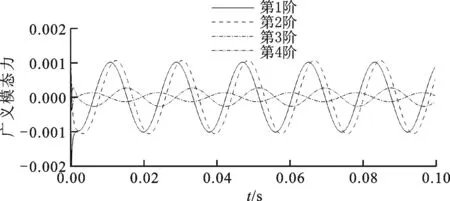
(b)Δt=1×10-5 s图5 不同时间步长对计算结果的影响

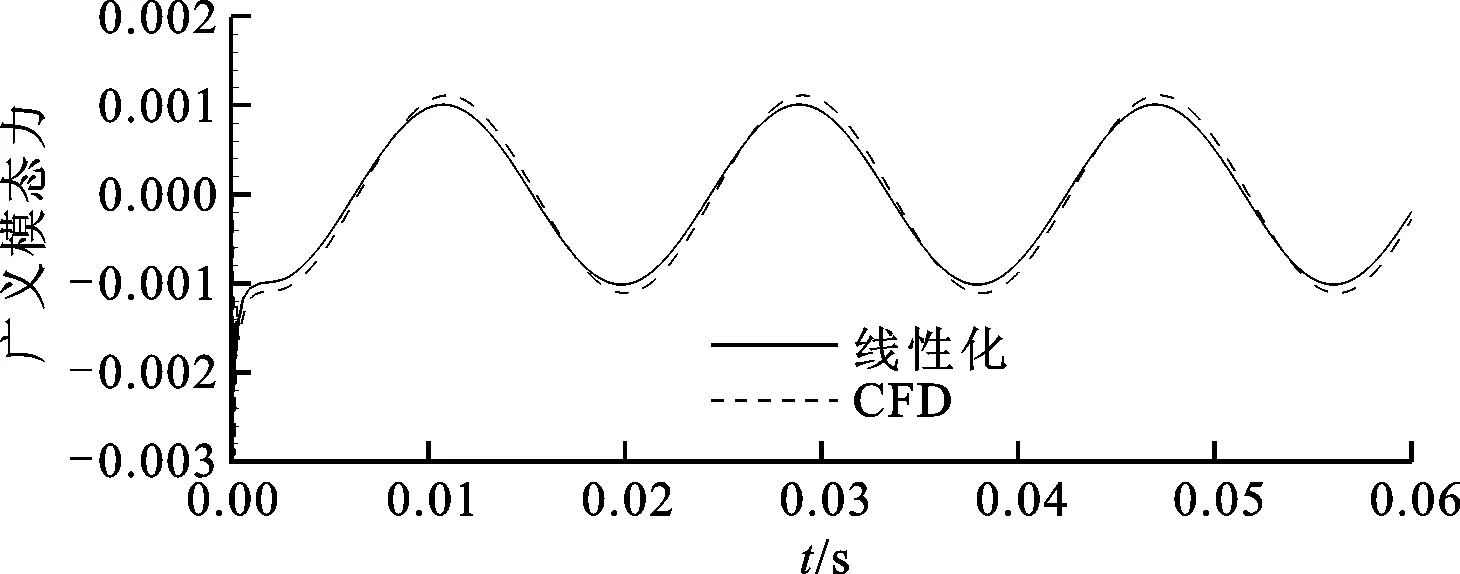
(a)第1阶广义模态力响应

为了验证全阶线性化模型建立的正确性,并计算其在指定模态位移下的非定常气动力响应,比较了不同时间步长下的响应,结果如图5所示。由图5a可看出,在时间步长较大时,广义气动力在开始阶段出现了非常大的数值振荡,随着时间的延长,响应曲线逐渐光滑;由图5b可看出,采用较小时间步长的气动力响应与CFD结果接近。由此可知,时间步长越小,越能有效抑制数值振荡现象,维持数值稳定性,故本文线性化和降阶响应计算的时间步长取为1×10-5s。线性化模型计算结果与非定常CFD结果的比较如图6所示,不同模型计算的前两阶广义模态力吻合得较好,验证了所建线性化模型具有和CFD相同的计算精度,为降阶计算及降阶气弹响应提供了高精度的数值模型。

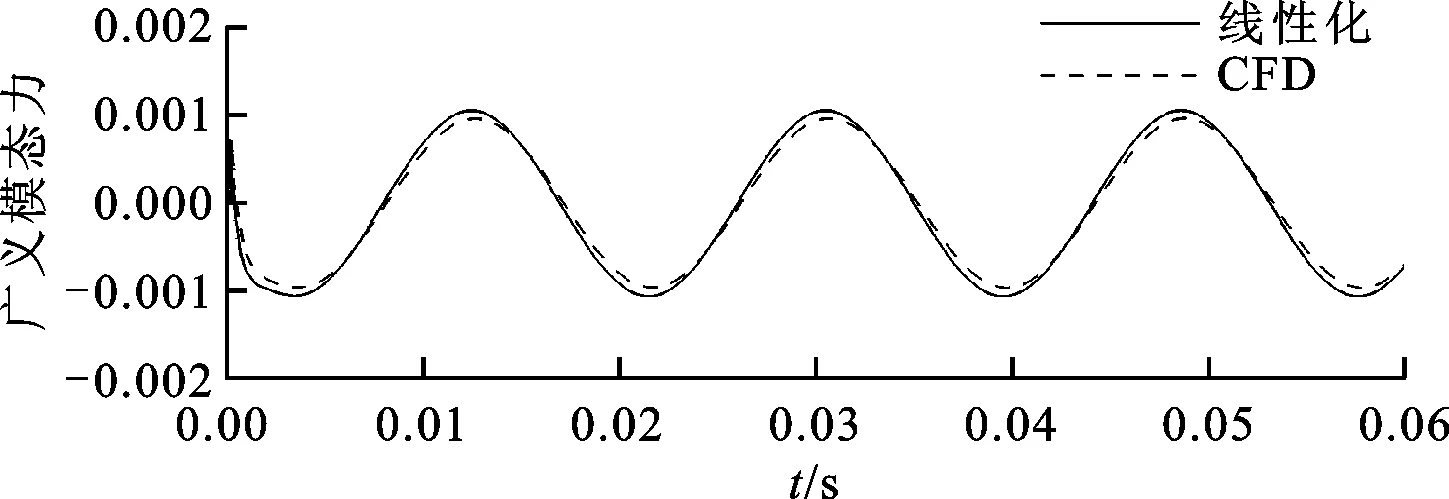
(b)第2阶广义模态力响应图6 线性化模型与非定常CFD计算响应比较

3.3 样本数据采集的影响

POD降阶方法需选择一组试验数据样本集,如何选择合适的数据来构造转换矩阵,对结果影响很大。线性化结果和CFD结果比较可知,小扰动下二者结果相差不大,故本文采用CFD线性化模型代替非线性CFD/CSD耦合模型。对全阶线性化系统方程给予不同的模态位移脉冲激励,采集不同时刻的响应数据,利用所得一系列样本数据,通过POD算法得到转换矩阵,进而将高维度的全阶系统转换成低维度的ROM。不同的样本采集间隔对降阶气弹响应的影响如图7所示,该降阶系统阶数为500。由图7可看出,样本采集间隔的选取对结果基本上没有太大影响,只要保证总响应时间相同,时间步长选取在合理范围对气弹响应结果影响不大。

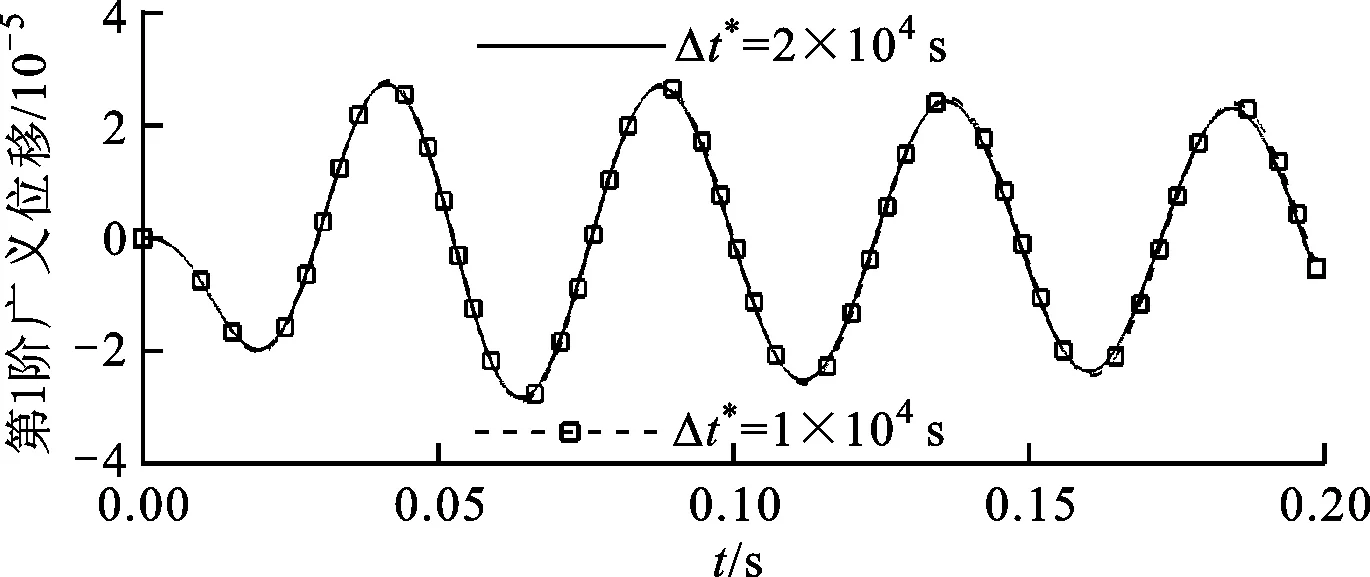
图7 样本采集间隔不同对结果的影响

4 降阶结果分析与颤振预测

4.1 不同阶数结果比较

由POD降阶数学理论可知,POD计算的奇异值百分比εp按从大到小依次排列,如图8所示,对应数值越大所反映的系统能量越多,高阶以后所反映的能量可忽略不计。不同阶数的降阶系统在马赫数为0.678、来流速度为240 m/s状态下气动弹性响应如图9所示。由图9可看出,300阶与500阶降阶系统结果随着时间变化出现明显的差异,且差异越来越大,而580阶与500阶结果几乎没有差异,一直保持同一响应趋势。因此,降阶系统阶数越高,其精度越高,而超过一定阶数后提高阶数对结果影响不大。

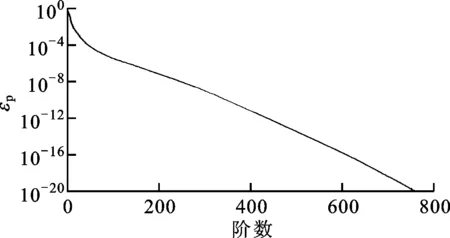
图8 Hankel 奇异值百分比分布

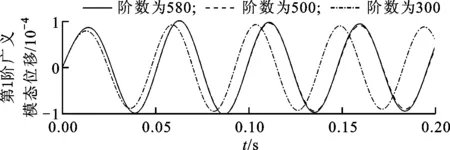
图9 不同阶数结果预测比较

4.2 颤振边界预测

给定马赫数和攻角,采用POD/ROM建立的气动弹性降阶系统,可通过改变动压,并观察其在不同动压下的响应来寻找颤振动压。给降阶系统一个小的初始扰动,本文以1阶模态速度作为扰动,不同动压下的气弹响应如图10所示。与CFD/CSD耦合计算一样,降阶系统响应趋势随着动压的改变而改变。Ma=0.678、V=250 m/s时,其响应出现发散,全阶和降阶系统吻合得非常好;当V减小到230 m/s时,系统响应出现收敛现象。临界颤振速度在230～250 m/s之间时,通过试算可得该状态下速度为240.8 m/s,而通过CFD/CSD耦合计算得到的结果约为240 m/s,此结果非常接近。这说明对于颤振预测,本文所建ROM和CFD/CSD耦合计算具有同样的精度。ROM求解该响应过程,计算时间约为2 s,而CFD/CSD耦合计算时间约为16.7 h。而且,指定马赫数下建立的ROM对动压参数变化具有高保真性,可快速预测不同动压的响应,方便地找到颤振边界,计算效率提高了几个量级。

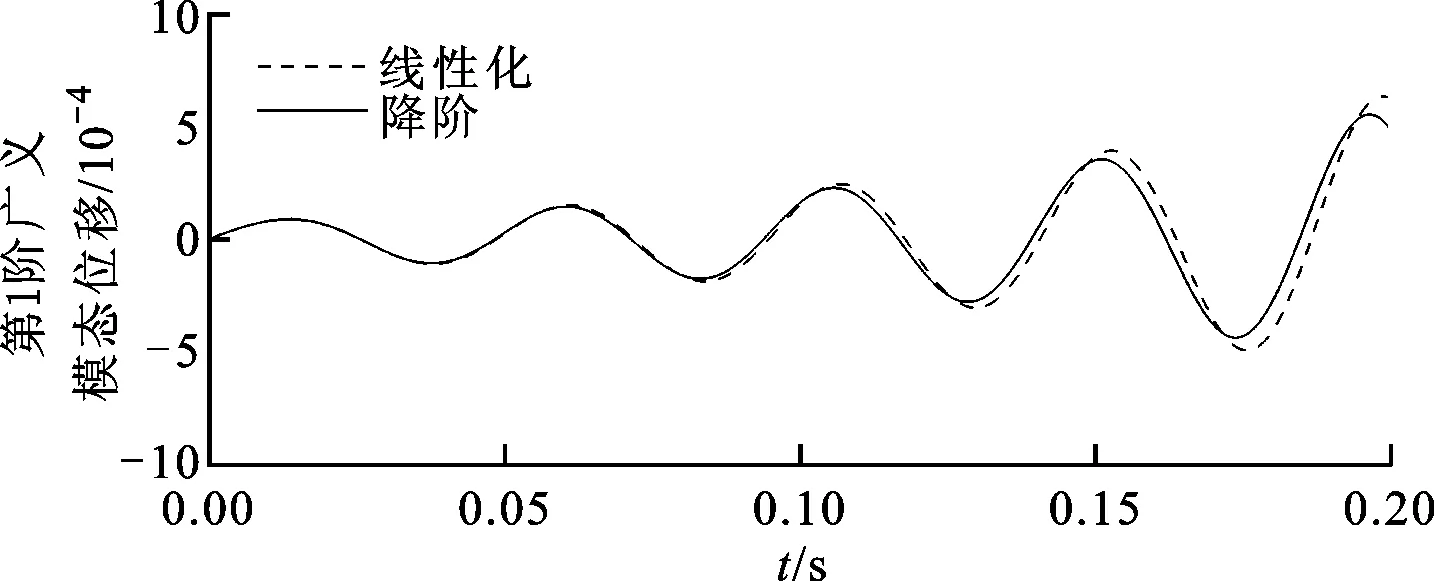
(a)V=250 m/s

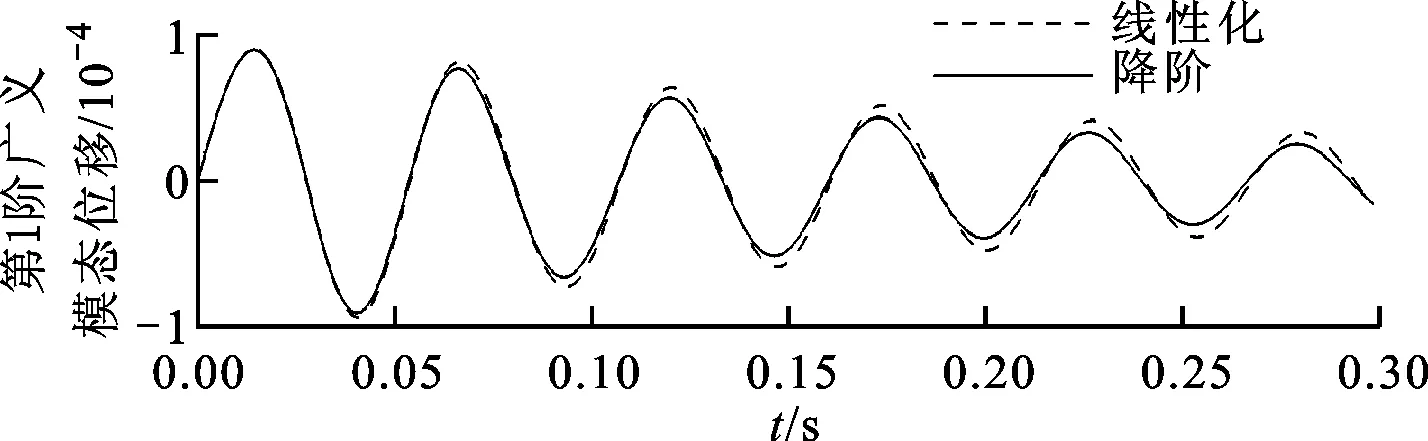
(b)V=230 m/s图10 不同动压下的气弹响应

在不同马赫数下建立相应的降阶模型,通过改变动压来预测颤振边界,可得所研究系统随马赫数变化的颤振边界,颤振速度作归一化处理,结果如图11所示,降阶模型预测的结果和CFD/CSD耦合计算的结果非常接近。

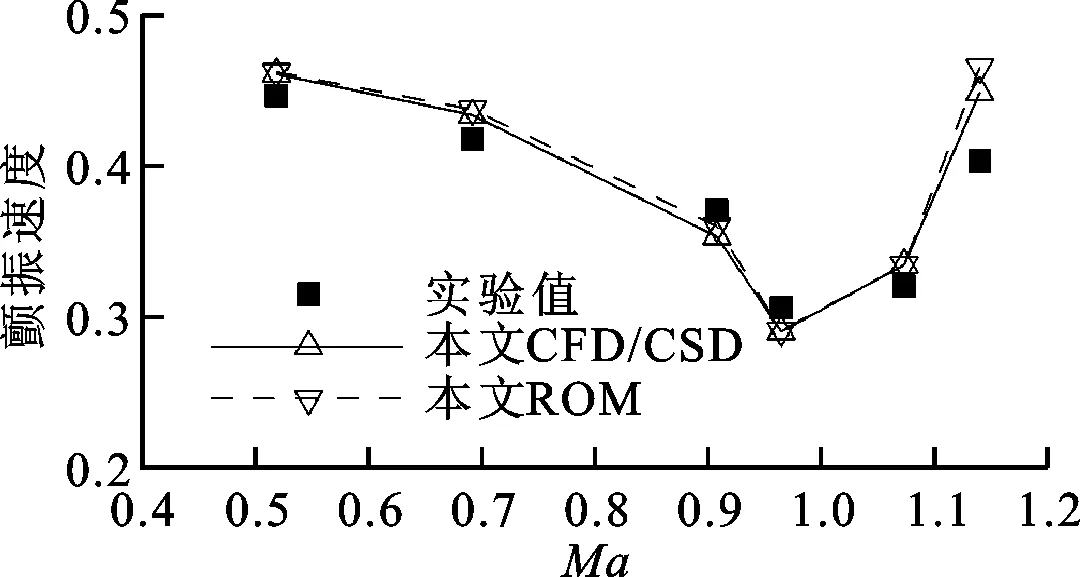
图11 AGARD 446.5机翼颤振边界比较

5 结 论

本文通过POD降阶方法建立了基于CFD的气动弹性ROM。以三维标模AGARD 445.6机翼为研究对象,系统研究了ROM建模过程中几个重要参数对降阶精度的影响。流场的收敛性对线性结果影响很大,流场收敛性不够易导致线性化响应结果发散;响应计算中时间步长过大易导致数值结果在开始阶段剧烈振荡;对于产生的样本数据,总的响应时间一样,样本采集间隔选取在合理范围对气弹响应结果影响不大,所以数据的产生必须保证足够的响应时间。

ROM与非线性CFD/CSD耦合计算结果比较分析表明:POD/ROM能很好保持原始非线性系统动力学特性,与CFD/CSD耦合计算具有相同的精度;计算效率上,ROM提高了3～6个量级,将数百万阶的大型系统降阶成数百阶低维系统,可直接应用于气动弹性快速分析和多学科设计上。

[1] 杨国伟. 计算气动弹性若干研究进展 [J]. 力学进展, 2009, 39(4): 406-420. YANG Guowei. Recent progress on computational aeroelasticity [J]. Advances in Mechanics, 2009, 39(4): 406-420.

[2] 周强, 陈刚, 李跃明. 考虑流固耦合效应的某飞行器力学性能分析 [J]. 应用力学学报, 2015(2): 209-214. ZHOU Qiang, CHEN Gang, LI Yueming. Considering fluid-structure coupling effect of an aircraft mechanical properties analysis [J]. Chinese Journal of Applied Mechanics, 2015(2): 209-214.

[3] SILVA W A, BARTELS R E. Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code [J]. Journal of Fluids and Structures, 2004, 19(6): 729-745.

[4] LUCIA D J, BERAN P S, SILVA W A. Reduced-order modeling: new approaches for computational physics [J]. Progress in Aerospace Sciences, 2004, 40(1): 51-117.

[5] 陈刚, 李跃明. 非定常流场降阶模型及应用研究进展与展望 [J]. 力学进展, 2011, 41(6): 686-701. CHEN Gang, LI Yueming. Advances and prospects of the reduced order model for unsteady flow and its application [J]. Advances in Mechanics, 2011, 41(6): 686-701.

[6] CHEN G, SUN J, LI Y. Active flutter suppression control law design method based on balanced proper orthogonal decomposition reduced order model [J]. Nonlinear Dynamics, 2012, 70(1): 1-12.

[7] 陈刚, 李跃明, 闫桂荣, 等. 基于POD降阶模型的气动弹性快速预测方法研究 [J]. 宇航学报, 2009, 30(5): 1765-1770. CHEN Gang, LI Yueming, YAN Guirong, et al. A fast aeroelastic response prediction method based on proper orthogonal decomposition reduced order model [J]. Journal of Astronautics, 2009, 30(5): 1765-1770.

[8] LIEU T. Adaptation of reduced order models for applications in aeroelasticity [D]. Denver, Colorado, USA: University of Colorado, 2004.

[9] AMSALLEM D, FARHAT C. Interpolation method for adapting reduced-order models and application to aeroelasticity [J]. AIAA Journal, 2008, 46(7): 1803-1813.

[10]康伟, 张家忠, 李凯伦. 利用本征正交分解的非线性Galerkin降维方法 [J]. 西安交通大学学报, 2011, 45(11): 58-62. KANG Wei, ZHANG Jiazhong, LI Kailun. Nonlinear Galerkin method for dimension reduction using proper orthogonal decomposition [J]. Journal of Xi’an Jiaotong University, 2011, 45(11): 58-62.

[11]丁鹏, 陶文铨. 求解对流换热反问题的低阶模型 [J]. 西安交通大学学报, 2009, 43(3): 14-16. DING Peng, TAO Wenquan. Reduced order model based algorithm for inverse convection heat transfer problem [J]. Journal of Xi’an Jiaotong University, 2009, 43(3): 14-16.

[12]周强, 陈刚, 李跃明. 复杂外形飞行器跨音速气动弹性CFD/CSD耦合数值模拟研究 [C]∥第十三届全国空气弹性学术交流会会议. 哈尔滨: 中国空气动力学会, 2013: 534-539.

[13]LIANG Y C, LEE H P, LIM S P, et al. Proper orthogonal decomposition and its applications: I theory [J]. Journal of Sound and Vibration, 2002, 252(3): 527-544.

(编辑 赵炜)

Effects of Some Parameters on the Accuracy of Aeroelastic Proper Orthogonal Decomposition Reduced Order Model

ZHANG Hongzhi1,2,ZHOU Qiang1,2,CHEN Gang1,2,LI Yueming1,2

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China; 2. School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China)

To quickly analyze the flutter boundary condition and response characteristics of transonic nonlinear aeroelastic systems, a CFD based aeroelastic reduced order model (ROM) was built in this paper through a proper orthogonal decomposition (POD) method. To implement this process, a full order linearized time domain model was built firstly by Taylor expression on the nonlinear steady CFD flow field; then a fluid ROM was obtained through the POD method Afterwards, an aeroelastic ROM was built by coupling the fluid ROM with structural dynamic equations. An international standard model AGARD 445.6 wing was taken as the test case to illustrate the results. Some important parameters in ROM establishment such as steady flow field, time step and the process of generation of sample dates were systematically studied. The research indicates that if the steady flow field doesn’t have good convergence performance, the linearized model may have unstable and that the responses may have numerical oscillation and become unstable as the large time step is selected in the ROM calculation. In order to capture more flow characteristics of the flow field, the generation of POD sample dates should ensure adequate response time. The ROM built in this paper has the same accuracy with the nonlinear CFD/CSD coupling system and it is a low order state space model which can be applied to system characteristics analysis and flutter suppression design. Compared with CFD/CSD coupled method, the computational efficiency can be improved about 3 to 6 orders.

CFD/CSD coupling; reduced order model; proper orthogonal decomposition; flutter

2016-05-11。 作者简介:张鸿志(1989—),男,硕士生;陈刚(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(11272005,11472206,11371288,11511130053);陕西省自然科学基金资助项目(2016JM1007)。

10.7652/xjtuxb201611016

V211

A

0253-987X(2016)11-0104-06