数控机床几何精度的位姿测量原理

李海涛,郭俊杰,邓玉芬,王金栋,何欣荣,王兴

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.西南交通大学机械工程学院,614202,成都;3.西安建筑科技大学建筑设计研究院,710055,西安)



数控机床几何精度的位姿测量原理

李海涛1,郭俊杰1,邓玉芬1,王金栋2,何欣荣3,王兴1

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.西南交通大学机械工程学院,614202,成都;3.西安建筑科技大学建筑设计研究院,710055,西安)

为了获得数控机床全部的几何误差信息,根据激光跟踪仪的三维空间测量特性,提出一种数控机床几何精度位姿测量原理和几何误差分离原理。借助于一台固定安装于机床上的数控精密转台和一台激光跟踪仪获得机床运动轴的位姿信息,然后辨识出机床各项几何误差。首先,详细描述了位姿测量方法的基本原理,给出了平动轴误差测量数学模型,包括测量点、基点空间坐标的标定原理以及姿态偏差的获取步骤;然后,根据解析几何知识先后分离出3项转角几何误差和3项位置几何误差,并综合得出单个运动轴6项几何误差分离模型;最后通过数值模拟、测量实验以及对比实验验证了该原理的可行性和准确性。实验表明,采用位姿测量原理可以在2 h内实现一台3轴高速数控铣床的精度检测,并准确分离出各项误差。位姿测量原理具有很高的测量精度与效率,解决了基点标定难题,且标定精度更容易提高。该原理为数控机床精度检测提供了一种新的思路,应用前景广阔。

位姿测量原理;几何精度检测;数控精密转台;激光跟踪仪

制造业的高速发展和加工水平的快速提高,对数控机床加工精度提出了越来越高的要求。通过对机床各项误差的快速检测并补偿是提高机床加工精度的有效手段[1]。

目前,机床几何误差的检测工具和仪器很多,测量直线运动误差的常用检测工具有测微仪、标准刻线尺、步距规、光学读数显微镜、准直仪、孔球板及双频激光干涉仪等,而测量回转运动误差的常用检测工具有高精度标准分度转台、高精度双球规和平面光栅等。这些仪器的优点是直接检测精确、明了,但需要测量仪器多、耗时长、效率低下且通用性差,不能满足机床各项误差快速、高精度、全面测量的检测要求[2-5]。

激光跟踪仪由于其高精度及其空间跟踪特性逐渐被应用于机床误差检测领域[1],德国联邦物理研究院利用激光跟踪仪在不到2 h的时间内即可对一台3轴机床的误差完成标定,并且具有很高的检测精度[6-7]。近年来,基于激光跟踪仪的检测机床的方法被大量研究,如激光跟踪单站法,基于多边法原理的激光跟踪仪多站法[8],为了降低成本,Schwenke提出了基于单台激光跟踪仪的分时测量原理[6,9],国内西安交通大学的王金栋、郭俊杰也对此进行了深入的研究[10-11],并基于九线法误差分离原理成功分离出平动轴和旋转轴各项误差,但算法和计算量较大。王金栋和林永兵都是通过机床坐标进行基点标定,标定过程中引入了机床本身的误差,影响最终的测量精度[8-12]。

本文提出一种位姿测量原理,借助于数控精密转台和一台激光跟踪仪,基于多站分时测量方法来检测数控机床各个运动轴的实时位姿信息,并提出一种新的误差分离方法,先后分离出3项转角误差和3项位置误差。同时,还提出一种基于数控精密转台的基点标定方法,解决了标定难题。最后,通过对位姿测量原理进行建模、分析、仿真和实验,验证了该方法的可行性与准确性。

1 位姿测量原理

激光跟踪三维坐标测量系统可分为单站和多站两种。单站法测量精度由于转角精度的限制,检测过程中精度难以保证[13]。多站法测量仅利用激光跟踪仪的测距信息,因此测量精度较高。为了降低成本,本文采用多站分时测量法来获取目标点的空间坐标[10-11]。

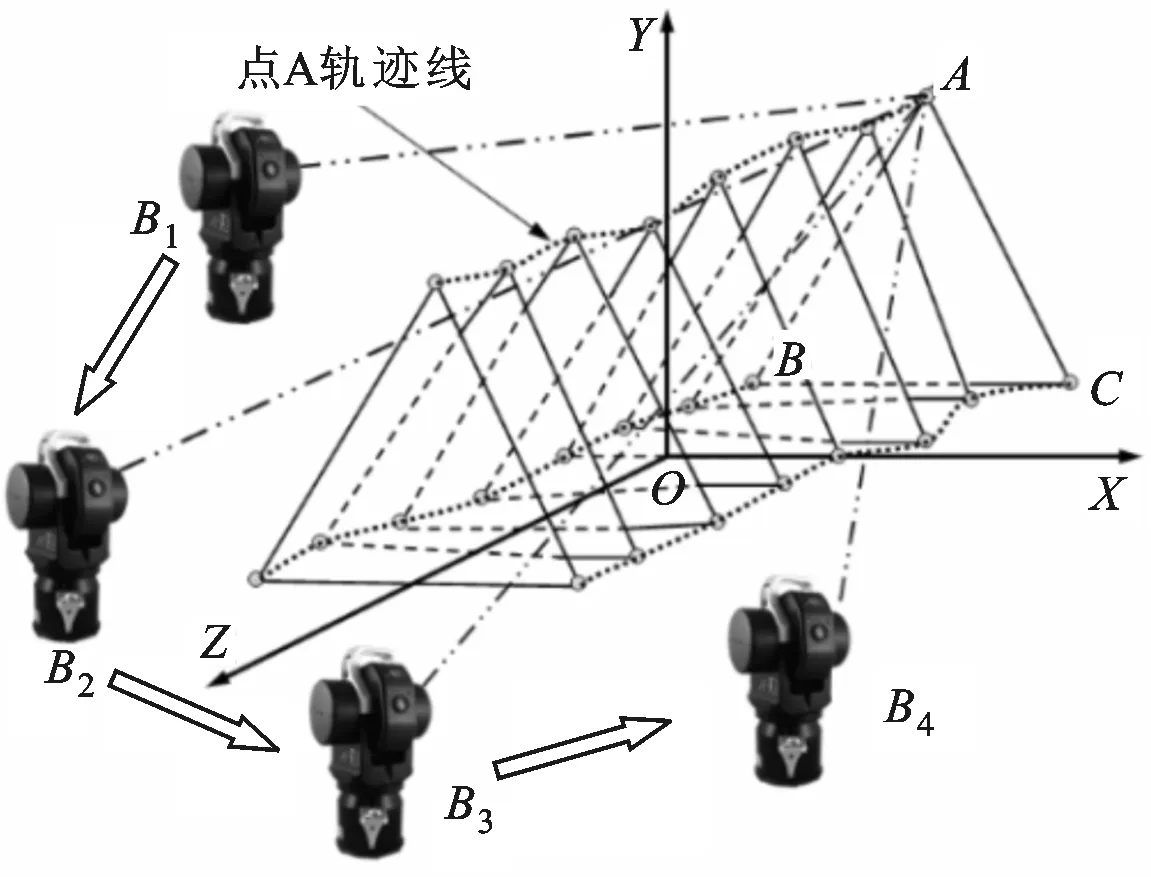
图1 数控机床单轴几何精度位姿测量原理

本文利用单台激光跟踪仪获取运动轴上3个目标点坐标值,然后进一步求取运动轴的位姿信息。图1为数控机床单轴几何精度位姿测量原理图,图2为移动轴位姿测量原理数学模型,图中OXYZ为数控精密转台坐标系,O0X0Y0Z0为机床坐标系。控制机床分别沿XYZ方向进给,并在运动轨迹上等间距进行数据采样。图2中P1、P2、P3、P4为测量时激光跟踪仪的4个基点位置,A0、B0、C0为靶镜所处的3个不同位置。以测量X轴为例,当激光跟踪仪在P1处时,测量P1与初始目标点A0的距离,同理,当A0分别运动至B0、C0处时,分别测量P1与B0、C0的距离,然后控制机床沿X轴运动至下一位置,重复以上测量过程直至X轴测量完成。

图2 移动轴位姿测量原理数学模型

2 位姿测量算法

首先,从几何误差的定义出发,用位姿偏差的概念重新描述了6项几何误差,理论分析了这种表示法的合理性。其次,理论描述了位姿偏差的获取方法。最后,简要说明了测量点以及基点空间坐标的标定原理与算法。

2.1 几何误差与位姿偏差

机床移动部件在导轨上移动时有6项几何误差元素[14],以X轴为例,如图3所示,包括3项移动误差(位置偏差),分别为定位误差δx(x)和两项直线度误差δy(x)与δz(x),以及3项转角误差(姿态偏差),分别为倾斜误差εx(x)、俯仰误差εy(x)和偏摆误差εz(x)。机床移动部件的6项误差即为位置偏差与姿态偏差的综合,因此可以用位置偏差与姿态偏差(即位姿偏差)描述6项误差元素。

图3 X轴的6项几何误差

如图4所示,用一个空间矢量V代替机床移动部件的姿态偏差,以X轴为例,根据3项转角误差的定义,εx(x)为V所在平面A1B1C2D2与XOY平面的夹角,εy(x)为V所在平面A1B2C2D1与XOY平面的夹角,εz(x)为V所在平面A1A2C2C1与XOZ平面的夹角。因此,3项转角误差可以表示为姿态偏差矢量V(x)=[εx(x),εy(x),εz(x)]T。3项移动误差可以表示为位置偏差矢量P(x)=[δx(x),δy(x),δz(x)]T。那么,对于X移动轴上任一点误差可以表示为

E(x)=[P(x),V(x)]T=

[δx(x),δy(x),δz(x),εx(x),εy(x),εz(x)]T

图4 转角误差与姿态偏差矢量

2.2 姿态偏差的获取

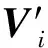
2.3 测量点空间坐标标定

通过多站分时测量的方法对固定点A、B、C的坐标进行求取。所谓多站分时测量,就是通过一台激光跟踪仪先后在不同位置对同一点进行测量,具体原理介绍及算法参考文献[15-16]。

2.4 基点空间位置标定

要获得测量点的坐标位置,首先要确定4个基点的坐标位置,即基点位置标定。图5为基点空间位置标定原理图,靶镜中心距离回转中心为r,每隔θ角度进行一次测量,旋转一定角度后,便可以获取点A、B、C等点距离基点P的距离。以回转中心O为坐标原点、以OA所在的直线为Y轴,向上方向为Y轴正方向,以过O点、垂直于OA的直线为X轴,向右方向为X轴正方向,以过O点、垂直于XOY的直线为Z轴,依据右手螺旋法则建立标定坐标系。坐标系O0X0Y0Z0为机床坐标系。

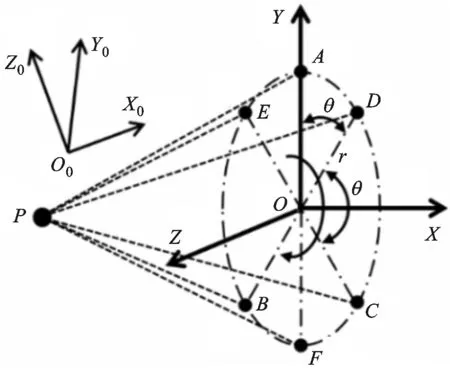
图5 基点空间位置标定原理

设激光跟踪仪初始距离读数为ΔL。激光跟踪仪所测量的点的距离读数分别为L1,L2,…,Ln(n≥6),设基站P在转台坐标系中的坐标为P(xp,yp,zp),按照两点距离公式得到超定方程组[12]

其中xp、yp、zp、ΔL、r为未知数,为了避免迭代初值的选定,采用解析的方法对上述非线性最小二乘问题进行求解,具体求解过程参见文献[12]。靶镜始终在同一个平面内旋转,求解过程中zp会出现正负两个解,根据所设立的坐标系,舍去负值。

3 误差分离算法

基于位姿测量原理的误差分离算法,首先求取运动轴所处位置的位姿偏差,然后根据姿态偏差分离出3项转角误差和两个逆转角度,再通过逆转角度值消除运动轴的姿态偏差,剩余的位姿偏差为位置偏差。

3.1 姿态偏差的求取

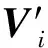
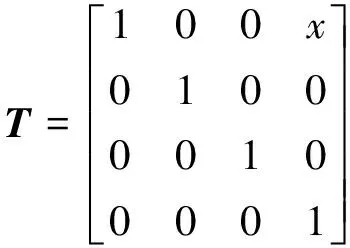
其中x为X轴的理论移动距离,所以姿态偏差为

3.2 转角误差分离

根据定义可得各项转角误差(转角误差的正负按照右手螺旋准则的规定)为

3.3 逆向旋转角度求解

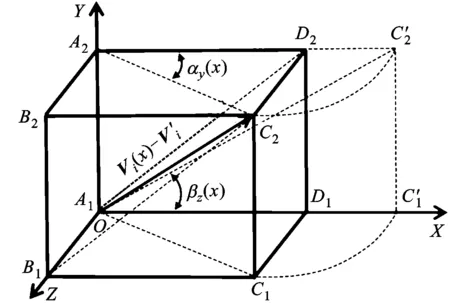
图6 逆向旋转角求解原理图

根据几何关系可得

ay(x)=arcan[(c(x)-k)/(a(x)-i-x)]

βz(x)=arctan[(b(x)-j)/((a(x)-i-x)2+

(c(x)-k)2)1/2]

3.4 移动误差分离

在机床坐标系中,将移动部件按照以上所求得的旋转角度按顺序逆向旋转,消除掉移动部件的转角误差。以点Ai为例,移动部件移动误差为

式中:αy与βz分别代表αy(x)与βz(x)。

3.5 误差分离数学模型

整理以上模型可得机床移动轴X轴的6项几何误差总的数学模型

4 数值模拟

采用数控精密转台对基点的坐标进行标定,采用四站分时测量的方法来确定机床测量点的坐标,对基点和测量点的标定过程进行了仿真实验验证。

4.1 基点空间位置标定

采用精密数控转台进行标定,解决了基点标定难题,数控精密转台实物如图7所示。为了方便测量同时获得更高的标定精度,转台采用合理的结构设计和精密制造技术,径跳和端跳都小于1 μm,采用内置电机和雷尼绍圆光栅形成位置闭环,圆周定位精度和重复定位精度也优于1 μm。

图7 数控精密转台实物图

如图7所示,靶镜安装在转台上,绕轴心每隔一定角度读取激光跟踪仪读数一次,共采集至少6个点的激光跟踪仪读数。根据基点空间位置标定算法进行计算,便可以标定出基点P的空间位置。

多次仿真实验发现,基点仿真坐标值和理论坐标值的最大偏差量级为10-10mm,两者几乎相等,说明算法是可行的。

为了标定的更加准确,在数控精密转台上会选择多于6个的采样点进行标定,同时,转台旋转多次,对同一位置进行多次测量,以减小随机误差的影响。为了验证标定算法的可靠性,对不同的采样点数、不同的测量次数以及随机误差的分布状况分多种工况进行仿真,仿真结果如表1所示。

表1 基点P位置标定偏差 mm

仿真实验表明:标定出的基点位置与理论位置偏差量随着随机误差的增大而增大;通过增加采样点数和测量次数都能非常明显地减小随机误差的影响,若继续增加,影响程度会越来越小。考虑到标定精度和测量效率,选择测量点数为9,测量次数为5。

4.2 测量点标定

设机床测量点的理想坐标为A(100,100,100)、B(100,500,100)、C(100,500,400)、D(300,500,400),分别从是否考虑机床随机误差两个方面进行仿真。

不考虑随机误差时,标定值和理想值最大偏差的数量级为10-11mm,两者几乎相等,说明算法是可行的。

考虑随机误差时,假设机床随机误差服从N(1.5,0.7)的正态分布,标定结果如表2所示。

表2 测量点标定结果 mm

各个测量点的位置坐标标定偏差几乎都小于3 μm,因此该算法具有一定的鲁棒性。

4.3 误差分离仿真

设机床在x=100 mm处,4个基点在机床坐标系中的位置坐标为P1(800,600,100)、P2(800,1 200,100)、P3(1 000,1 200,300)、P4(1 000,600,600)。为了验证算法的准确性,设此处X轴的各项误差为:定位误差δx(x)=0.024 mm,Y向直线度误差δy(x)=0.020 mm,Z向直线度误差δz(x)=0.016 mm,滚转角误差εx(x)=2×10-5rad,俯仰角误差εy(x)=2.4×10-5rad,偏摆角误差εz(x)=2.8×10-5rad。下面分两种情况进行仿真。

(1)不考虑随机误差:误差分离模型辨识出各项误差与假定的各项误差近乎相等,最大偏差量为δy(x)的偏差4.834 291 7×10-12mm,说明误差分离算法是可行的。

(2)考虑机床随机误差:假定机床运动过程中随机噪声服从N(2.5,1)和N(1.5,0.7)正态分布。表3给出了两种不同工况下几何误差分离的结果。

第1种工况分离出的误差最大偏差量δy(x)为0.000 132 mm,第2种最大偏差量δz(x)为0.000 54 mm,偏差量都比较小,算法可靠性较高。在实际测量中,为了进一步提高误差分离精度,会通过多次测量求平均值的方法减小随机误差对于测量结果的影响。

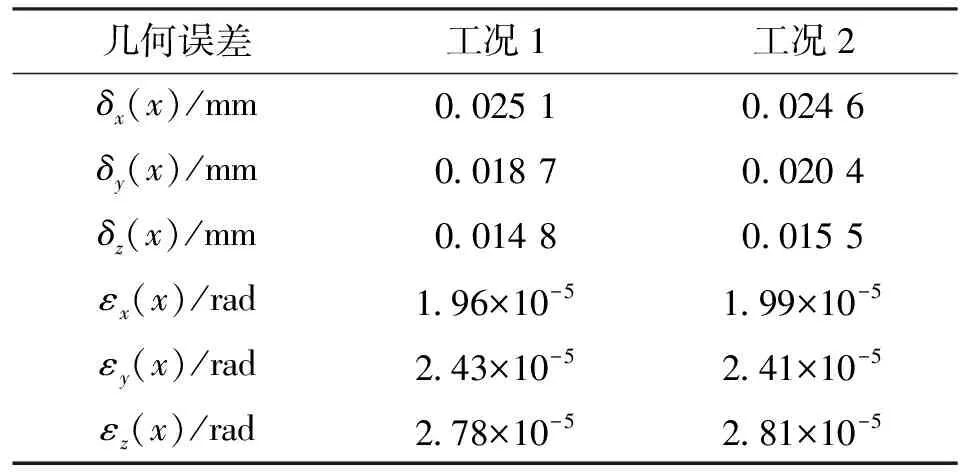
表3 X轴几何误差分离结果

5 实验验证

采用位姿测量原理对一台3轴高速铣床进行精度检测,如图8所示。4个基站在不影响测量过程的情况下应尽量分散,同时为了方便以后数据处理,4个基站不应设置在同一平面内。设定铣床运动区域为500 mm×500 mm×300 mm,每移动50 mm进行一次位姿测量。测量时机床停止运动,读取当前激光跟踪仪的读数,控制数控精密转台旋转120°,记录此时激光跟踪仪的读数,依次读取靶镜在3个不同位置的距离值,然后机床运动至下一测量位置。对于X轴,共需要测量33个点,对于整台机床共需要测量81个点,因为机床和数控精密转台都是数字控制,比较省时,加上移动基站的时间,完成所有测量需要2 h左右。

图8 应用激光跟踪仪检测机床精度

关于多站分时测量原理确定测量点空间坐标的可行性实验,文献[16]将多站分时测量方法标定出的测量点坐标和单站法测量出的坐标进行对比,验证了测量原理的可行性。

为了验证误差分离数据的准确性,将位姿法分离出的误差和一台激光干涉仪检测出的误差进行对比。图9所示为应用激光干涉仪检测3轴铣床运动时的定位误差,表4为两种方法部分测量点测量结果对比。

图9 应用激光干涉仪检测机床精度

表4 两种方法误差测量结果对比 mm

从表4中可以看出,两种测量法误差辨识结果最大偏差为2.8 μm,非常接近,说明采用位姿法进行机床误差测量与误差分离的方法是准确可行的。

6 结 论

(1)提出一种基于单台激光跟踪仪和数控精密转台测量数控机床几何精度的位姿测量原理,测量过程中只利用激光跟踪仪测距信息,测量精度高。

(2)提出一种基点标定方法,引入数控精密转台解决了激光跟踪仪基点位置标定问题,标定精度取决于数控精密转台本身的精度,与以往利用机床坐标轴信息进行标定的方法相比,标定精度更高。

(3)提出一种新的利用位姿偏差描述6项几何误差的表示方法和误差分离方法,给出几何误差的逐项分离算法,并通过仿真验证了该算法的可行性。

(4)采用单台激光跟踪仪实现了3轴高速铣床的快速检测,并在2 h完成机床的精度标定,分离出各项几何误差。同时,利用激光干涉仪对移动轴的定位误差进行测量实验结果对比,进一步验证了位姿测量原理的可行性、准确性。该方法具有快速、简单、精度高的特点,可以满足中高档数控机床几何误差的检测。

[1] SCHWENKE H, KNAPP W, HAITJEMA H, et al. Geometric error measurement and compensation of machine-an update [J]. CIRP Annals: Manufacturing Technology, 2008, 57(2): 660-675.

[2] TRAPET E, WALDELE F. A reference object based method to determine the parametric error components of co-ordinate measuring machines and machine tools [J]. Measurement, 1991, 9(1): 17-22.

[3] KUNZMANN H, TRAPET E, WALDELEF, Results of international comparison of ball plate measurements in CIRP and WECC [J]. Annals of the CIRP, 1995, 44(1): 479-482.

[4] FLORUSSEN F L M, DELBRESSINE M J G. Assessing geometrical errors of multi-axis machines by 3D length measurements [J]. Measurement, 2001, 30(4): 241-255.

[5] 朱嘉, 李醒飞, 谭文斌, 等. 基于激光干涉仪的测量机几何误差检定技术 [J]. 机械工程学报, 2010, 46(10): 25-30. ZHU Jia, LI Xingfei, TAN Wenbin, et al. Method of geometric error detection for measuring machine based on laser interferometer [J]. Journal of Mechanical Engineering, 2010, 46(10): 25-30.

[6] SCHWENKE H, FRANKE M, HANNAFORD J, et al. Error mapping of CMMs and machine tools by a single tracking interferometer [J]. CIRP Annals: Manufacturing Technology, 2005, 54(1): 475-478.

[7] LAU K, HOCKEN R J, HAIGHT W C. Automatic laser tracking interferometer system for robot metrology [J]. Precision Engineering, 1986, 8(1): 3-8.

[8] 张国雄, 林永兵, 李杏华, 等. 四路激光跟踪干涉三维坐标测量系统 [J]. 光学学报, 2003, 23(9): 1030-1036.

ZHANG Guoxiong, LIN Yongbing, LI Xinghua, et al. Four-beam laser tracking interferometer system for three-dimensional coordinate measurement [J]. Acta Optica Sinica, 2003, 23(9): 1030-1036.

[9] SCHWENKE H, SCHMITT R, JATZKOWSKI P, et al. On-the-fly calibration of linear and rotary axes of machine tools and CMMs using a tracking interferometer [J]. CIRP Annals: Manufacturing Technology, 2009, 58(1): 477-480.

[10]王金栋, 郭俊杰, 邓玉芬, 等. 应用激光跟踪仪的数控机床几何精度检测 [J]. 西安交通大学学报, 2011, 45(3): 85-90. WANG Jindong, GUO Junjie, DENG Yufen, et al. Geometric precision detection for numerical control machine tool based on laser tracker [J]. Journal of Xi’an Jiaotong University, 2011, 45(3): 85-90.

[11]WANG Jindong, GUO Junjie, ZHANG Guoxiong, et al. The technical method of geometric error measurement for multi-axis NC machine tool by laser tracker [J]. Measurement Science and Technology, 2012, 23(4): 45003-45013.

[12]林永兵, 张国雄, 李真, 等. 四路激光跟踪干涉三维坐标测量系统自标定与仿真 [J]. 仪器仪表学报, 2003, 24(2): 205-210. LIN Yongbing, ZHANG Guoxiong, LI Zhen, et al. Self-calibration and simulation of the four-beam laser tracking interferometer system for 3D coordinate measurement [J]. Chinese Journal of Scientific Instrument, 2003, 24(2): 205-209.

[13]张国雄. 三坐标测量机 [M]. 天津: 天津大学出版社, 1999: 307-310.

[14]杨建国, 范开国, 杜正春. 数控机床误差实时补偿技术 [M]. 北京: 机械工业出版社, 2013: 20-28.

[15]刘永东, 王佳, 梁晋文. 动态几何量多站法激光跟踪测量自标定 [J]. 光学技术, 1999, 23(3): 25-27. LIU Yongdong, WANG Jia, LIANG Jinwen. Self-calibration of multi-station laser tracking system for dynamic geometric measurement [J]. Optical Technique, 1999, 23(3): 25-27.

[16]王金栋, 郭俊杰, 费致根, 等. 基于激光跟踪仪的数控机床几何误差辨识方法 [J]. 机械工程学报, 2011, 47(14): 13-19. WANG Jindong, GUO Junjie, FEI Zhigen, et al. Method of geometric error identification for numerical control machine tool based on laser tracker [J]. Journal of Mechanical Engineering, 2011, 47(14): 13-19.

(编辑 荆树蓉)

Pose Measuring Principle of Geometric Accuracy of Numerical Control Machine Tools

LI Haitao1,GUO Junjie1,DENG Yufen1,WANG Jindong2,HE Xinrong3,WANG Xing1

(1. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 614202, China; 3. Design Institute of Xi’an University of Architecture and Technology, Xi’an 710055, China)

In order to obtain all geometric errors of numerical control (NC) machine tool, according to the 3D measurement characteristic of laser tracker, the pose measurement principle for geometric accuracy detection of machine tool and separation principle for geometric error are developed. By means of NC precise turntable fixed on machine tool and a laser tracker, the pose information of translational axis can be calculated, then the geometric errors are determined. First, the pose measurement principle and measurement mathematical model of linear axis are developed in details, including calibration principle of measuring points and base stations, and the acquisition procedures of pose deviation. Then, the three angular errors and three linear errors are identified successively and geometrically, and the comprehensive error identification model for single axis is determined. At last, the feasibility and veracity are verified by simulation experiment, measurement experiment and comparative experiment. Results of experiments show that the proposed method is able to complete the precision detection of a 3-axis milling machine within 2 h, and the errors are identified successfully. This measurement principle has short measurement time and high precision, and solve the calibration problem of base station with higher precision. The pose measurement principle provides a new method for machine tool error detection with an extensive application prospect.

pose measuring principle; geometric accuracy detection; numerical control precision turntable; laser tracker

2016-04-12。 作者简介:李海涛(1987—),男,博士生;郭俊杰(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51305370);国家科技重大专项资金资助项目(2015ZX04005001)。

时间:2016-07-18

10.7652/xjtuxb201611010

TH161.21

A

0253-987X(2016)11-0062-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160718.1013.006.html