吃透概念方能百密无疏——兼谈加强轨迹概念理解性教学的策略

刘华为（上海市岭南中学）

吃透概念方能百密无疏
——兼谈加强轨迹概念理解性教学的策略

刘华为（上海市岭南中学）

加强概念理解性教学，在概念的形成过程和应用中，不断挖掘概念理解的高度、深度和宽度.再引导学生从核心概念入手，追根溯源，寻求问题解决的本质，也是培养学生发现问题和解决问题能力的重要途径之一.

概念理解性教学；动点轨迹；知识溯源

一、问题提出

题目如图1，等边△ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P.若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长.

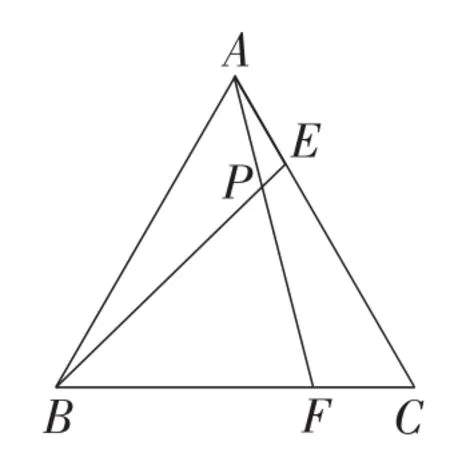
图1

图2

错解：若AF=BE，则主要有AE=BF和AE=CF两种情形.如图2，当AE=BF时，点P经过的路径为AB边上的高CH，长为当AE=CF时，点P的路径为以A，B为端点，且所对圆心角为120°的根据图中所作辅助线可求得其长为综上所述，点P经过的路径长为或

错解剖析：众所周知，若点集A称为具备性质p的点的轨迹必须满足两点：第一，纯粹性（集合A内所有的点都必须满足性质p）；第二，完备性（所有满足性质p的点都属于集合A）.由此可知，点P的轨迹应是所有满足条件AF=BE所产生的点的集合.即当点E从点A运动到点C时，符合条件的点P不是一个，而是有两个点P1，P2，它们分别从点A和点H各自沿和△ABC的高CH运动，所以动点P的路径是由和高CH共同所组成的图形，其长为两者之和，即不应分开表述.

显然，错解违背了轨迹定义的“完备性”，犯了概念理解不透之误.下面笔者就如何加强轨迹概念理解性教学的策略谈几点拙见，以求抛砖引玉.

二、教学策略

1.借助作图降低轨迹概念理解的难度

由于轨迹的概念比较抽象，学生理解起来有一定的难度.但对于具体问题，若能在黑板上展示作图的过程，呈现出轨迹的完整图形，并辅以几何画板软件的动态演示，对学生理解轨迹概念必能起到事半功倍的效果.例如，学生对于题目“当AE=CF时，点P的路径为以点A，B为端点且所对圆心角为120°的弧”理解上就有一定的难度.教学中若借助于几何画板软件，对点E生成动画，再追踪点P，则点P的轨迹便形象、直观、动态地展示在学生的眼前（如图3），再引导学生推导∠APB=120°，从理论上加以证明.如此处理，不仅能激发学生的学习兴趣，而且对加深理解也大有裨益.

图3

2.借助反例加深轨迹概念理解的深度

对于轨迹的“纯粹性”和“完备性”，即使教师反复强调，学生也未必能体会其中的奥秘.相反，若能把它们渗透于反例的辨析中，则可化抽象为具体，对理解和掌握这两个性质大有裨益.例如，借助“以线段AB为底边的等腰三角形顶点C的轨迹是线段AB的中垂线”的辨析可加深对轨迹“纯粹性”的理解，借助“以长为c的线段AB为边且面积为S的△ABC顶点C的轨迹是一条平行于AB，且到AB的距离为的直线”的辨析可加深对轨迹“完备性”的理解.

3.借助溯源提升轨迹概念理解的高度

一般地，数学习题是由教材的有关知识、信息、符号，通过迁移、发散和综合而来的，因此，相关问题的知识源就是解决此类问题的最佳策略和制胜法宝.而初中阶段与轨迹有关的知识源主要有：（1）到线段两端点距离相等的点的轨迹为这条线段的中垂线；（2）在角的内部且到角的两边距离相等的点的轨迹是这个角的平分线；（3）到直线距离相等的点的轨迹是两条平行于该直线且到它的距离相等的直线；（4）到定点距离等于定长的点的轨迹是以定点为圆心、定长为半径的圆；（5）对已知线段的张角为定值的动点轨迹是以该线段端点为端点的弧（该弧所对圆心角度数与张角度数相等）等.

题目中问题又适用哪个知识源呢？当AE=BF时，由几个特殊情况下点P的位置，可猜想其轨迹为直线型.而由已知条件、等边三角形的轴对称性和点P的位置特征，联想到知识源（1），即证明PA=PB.又易证△ABF≌△BAE，故∠BAF=∠ABE，从而得证；当AE=CF时，易判断点P的轨迹为非直线型.由∠APB=120°为定值联想到知识源（5），从而得点P的轨迹为所对圆心角也为120°的

【点评】通过追根溯源，不仅让学生知道怎样做，还让他们明白为什么要这样做，更重要的是让学生学会“怎么想”，为今后解决此类问题打开了思路，从而把对轨迹概念的理解提升到一个崭新的高度.

4.借助定义拓宽轨迹概念理解的宽度

（1）借助直线定义确定动点轨迹.

方法引领：事实上，若能吃透直线概念（直线是由一点沿着一定方向及其相反方向运动而产生的），就会明白要说明一动点轨迹为直线，则必须证明两点：第一，该轨迹恒过一定点（确定位置）；第二，轨迹上任一点与该定点的连线和一定直线的夹角相等或平行（明确方向）.

图4

图5

解：如图5，由点P位于点O，N时，点B所对应的位置为点B0，Bn，以及点P在线段OC上运动，可猜想点B的轨迹是线段B0Bn.理由如下.

由AB0=AO·tan30°，AB=AP·tan30°，

得AB0∶AO=AB∶AP=tan30°.

又易知∠OAP=∠B0AB.得△AB0B∽△AOP.

所以∠AB0B=∠AOP为定值.

又由点B0为定点，故点B在线段B0Bn上，即线段B0Bn就是点B运动的路径（或轨迹）.

同理，可证△AB0Bn∽△AON，且相似比为tan30°.

则B0Bn=ON·tan30°=

【点评】欲证线段B0Bn就是动点B的轨迹，考虑到点B已过定点B0，下面只需证明∠AB0B为定值，即证明它与某一个定角相等即可.观察可得∠AOP就是与∠AB0B相等的定角，再由两角的位置特征和题设条件，就不难想到用三角形相似来证明相等了.一般地，证明动点轨迹为直线（或线段）时，通常找动点的起始点或终点为定点来确定轨迹的位置；至于轨迹方向，除了像此题以证明∠AOP与定角∠AB0B相等来确定外，还可用与定直线平行来确定.

（2）借助圆的定义确定动点轨迹.

方法引领：除了题目中由圆周角为定值确定圆弧型轨迹外，还可根据圆的定义判定，即证明动点到某一定点的距离为定值.

例2如图6，已知正方形OABC的边长为2，顶点A，C分别在x，y轴的正半轴上，M是BC的中点. P（0，m）是线段OC上一动点（点C除外），直线PM交AB的延长线于点D.

图6

（1）求点D的坐标（用含m的代数式表示）；

（2）当△APD是等腰三角形时，求m的值；

（3）设过P，M，B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为点H（如图7），当点P从点O向点C运动时，点H也随之运动.直接写出点H所经过的路径长.

图7

解：（1）略.

（2）略.

（3）由OH⊥ME和点O，M为定点，联想到连接OM，取其中点N，则动点H到定点N的距离为定值，即点H的轨迹是以点N为圆心，以OM为半径的圆上的一段圆弧.

显然，当点P无限接近点C时，点E趋向无穷远，ME与x轴接近于平行，所以点H无限接近于点C；当点P与点O重合时，点H对应的位置点为轨迹的另一个端点.此时，可求得抛物线的解析式为y=-x2+3x，得点E的坐标为E（3，0）.

过点M作x轴的垂线交x轴于点F，可得∠FME=45°.

则∠CME=135°.

又因为∠OCM=∠MHO=90°，所以∠COH=45°.

连接CN，由CN=ON=HN，知∠CNM=2∠COM，∠HNM=2∠HOM.所以∠HNC=90°.

【点评】用圆的定义确定动点轨迹的关键是找定点（即圆心），通常可由动点所对的定线段为直径（即张角为直角）来找圆心.例如，此题就是抓住∠MHO为90°来确定线段MO为直径，从而找出圆心N.

（3）借助函数图象定义确定动点轨迹.

方法引领：由函数图象的定义可知，函数图象就是在直角坐标平面内由满足函数关系式的动点所产生的轨迹.因此，对于无法由特殊位置确定形状的动点轨迹，可适当建立平面直角坐标系，再根据动点横、纵坐标所满足的函数关系式及其图象来确定.

例3如图8，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ，分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）.

图8

（1）直接用含t的代数式分别表示：QB=_____，PD=_______.

（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由.并探究如何改变Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度.

（3）在整个运动过程中，求出线段PQ中点M所经过的路径长.

解：（1）略.

（2）略.

（3）显然中点M的轨迹不易直接判断形状，可采用间接法，即利用函数图象来处理.考虑到AC与BC互相垂直，故以点C为原点、直线CA为x轴建立平面直角坐标系（如图9），设点M的坐标为M（x，y）.

图9

过点M作MN⊥Ox于点N，则MN∥QC.

消去t，得y=-2x+6.又由0≤t≤4，得1≤x≤3.

所以点M的轨迹是以E（3，0），F（1，4）为端点的线段EF，由两点之间距离公式得点M经过的路径长

【点评】建立平面直角坐标系的原则是尽量利用垂线且有利于动点坐标求解；而求动点坐标通常需要过动点向坐标轴作垂线，再由垂线段的长和动点所在的象限而得.值得注意的是，由于是动点，其横、纵坐标必然是用某一变量（参数）来表示的，只需消去参数（即消元思想），即可得动点坐标所满足的函数关系式，从而求出动点的轨迹.

方法总评：综上所述，处理“求动点路径（轨迹）长问题”的策略主要为“一找（轨迹），二求（长度）”，其中找轨迹最为关键.那么如何确定轨迹的形状和位置呢？首先，根据条件思考能否依据所学过的一些特殊轨迹直接判定（如题目）.否则，可通过动点所在的几个特殊位置猜想其形状是直线型还是圆弧型.若为直线型，则先确定动点所经过的一个特殊点（通常为起点或终点），然后再证明动点与该特殊点连线与题中某一定直线的夹角为定值或平行（如例1）；若为圆弧型，则观察动点对某一定线段的张角是否为定值（如题目），或与某一定点的距离是否为定值（如例2）；若无法确定是否为两者之一，则可建立适当的直角坐标系，求出动点横、纵坐标所满足的函数关系式，利用图象确定动点轨迹（如例3）.

但不管怎样，应从核心概念入手，追根溯源，回归问题解决的本质，寻求解决问题的基本途径.

［1］余利英，姜鸿雁.对一道中考试题及其标准答案的思考［J］.中学数学教学参考（中旬），2014（7）：60-62.

［2］刘华为.中考压轴题：怎样解，为何这样解［M］.西安：陕西师范大学出版社，2014.

2016—09—14

刘华为（1968—），男，中学高级教师，主要从事课堂教学与命题研究．