运用模型思想驱动几何解题有效思考——以一道几何题的多种解法探究为例

李发勇（四川省巴中市巴州区大和初中）

运用模型思想驱动几何解题有效思考
——以一道几何题的多种解法探究为例

李发勇（四川省巴中市巴州区大和初中）

开放性几何解题对大多数学生来说难以获得思路突破，对学生最大的挑战是问题解决的几何模型不清晰.通过模型思想创设学生思维最近发展区，可以驱动学生有效思考.以一道经典问题的一题多解、拓展变式为例，突破学生思维障碍，提高学生几何解题的有效性.

模型思想；几何思考；思维障碍；有效性

波利亚在《数学的发现》中认为，中学数学教学的首要任务就在于加强解题训练.数学离不开解题，解题的灵魂是数学思想，而数学模型是思想的载体.在几何教学中，定义、定理、性质所代表的图形，以及在几何中经常遇到的经典图形和由实际问题抽象为几何图形表示的数学问题，我们都称之为几何模型.在平时的教学过程中，教师要善于引导学生将所学内容整理归纳出类型和方法，经过加工提炼，得出有指导价值、有典型结构的数学模型.当遇到一个几何图形问题时，我们要能辨认它属于哪一类基本模型，或是由哪些基本模型复合而成.以此为索引，驱动记忆贮存提取出相应的方法来加以解决，这就是利用数学模型解题的策略.

一、对一道经典试题模型的解法探究

题目如图1，在正方形ABCD中，E为边BC上任意一点，∠AEF=90°，EF交正方形外角平分线于点F.求证: AE=EF.

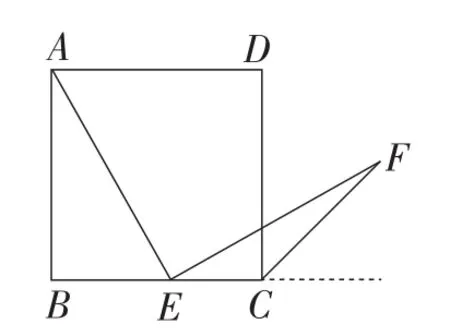
图1

1.相似模型：即利用相等角，构造相似三角形

利用隐含条件∠BAE=∠CEF，构造相似三角形，再根据相似比为1的三角形全等，获证相应的结论.

证法1：如图2，过点F作FG⊥BC，交BC的延长线于点G.

图2

因为∠AEF=∠B=90°，

所以∠BAE=90°-∠AEB=∠FEC.

又因为∠B=∠FGE=90°，

所以△ABE∽△EGF.

又∠FCG=∠CFG=45°，

所以CG=FG.

设EC=a，CG=b，

则BE=BC-EC=AB-a，EG=EC+CG=a+b，

从而得AB=a+b.

所以AB=EG.

所以△ABE≌△EGF.

故AE=EF.

证法2：如图2，过点F作FG⊥BC，交BC的延长线于点G.

由∠AEF=∠B=90°，得∠BAE=∠FEC，

即tan∠BAE=tan∠FEC，

又∠FCG=∠CFG=45°，

所以CG=FG.

设EC=a，CG=b，

则BE=BC-EC=AB-a，EG=EC+CG=a+b，

从而得AB=a+b.

所以AB=EG.

所以△ABE≌△EGF.

故AE=EF.

2.对称模型：利用垂直或角平分线建立轴对称图形

利用条件AB⊥BC，添加辅助线建立轴对称图形，再利用轴对称图形的性质，证明相应结论.

证法3：如图3，延长FC交AB延长线于点A′，

图3

则点A与点A′关于BC所在直线对称.

所以AE=A′E，∠EAB=∠BA′E.

所以∠EAB=∠FEC=∠BA′E，∠BA′C=∠BCA′=45°.

由∠F=∠FCH-∠FEC=45°-∠FEC，∠CA′E=∠BA′C-∠BA′E=45°-∠BA′E，

所以∠F=∠CA′E.

则A′E=EF，即AE=EF.

证法4：如图4，延长AC至点F′，使CF′=CF，连接EF′.

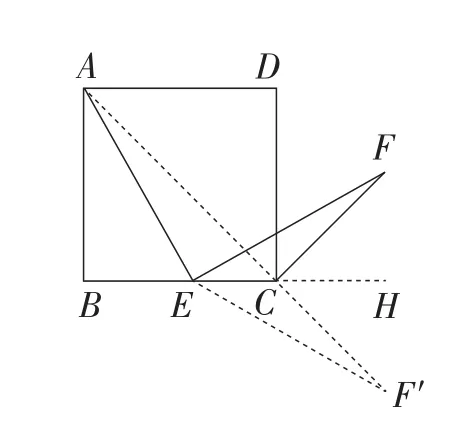
图4

因为∠FCH=∠F′CH=45°，

则点F与点F′关于BC所在直线对称.

所以EF=EF′.

因为∠EAB=∠FEC=∠CEF′，

且∠F′=∠F′CH-∠CEF′=45°-∠CEF′，∠CAE=45°-∠EAB，

所以∠F′=∠CAE.

则AE=EF′.

所以AE=EF.

3.全等模型：利用相等角，构造全等形

利用隐含条件∠EAB=∠FEH或AB=CB，添加辅助线构造全等三角形，利用全等三角形对应边相等，证明有关结论.

证法5：如图5，在AB上截取BP=BE，

图5

则∠BPE=∠BEP=45°，

因为AB=BC，

所以AP=CE.

因为CF是角平分线，

所以∠ECF=180°-∠FCH=135°.

又∠APE=180°-∠BPE=135°，

所以∠APE=∠ECF.

因为∠AEF=∠B=90°，

所以∠BAE=∠FEC.

所以△APE≌△ECF.

所以AE=EF.

证法6：如图6，在AB的延长线上截取BP=BE，

图6

则△ABE≌△CBP.

所以∠BAE=∠BCP，AE=CP.

又∠BAE=∠FEC，

所以∠FEC=∠BCP.

又∠CEP=∠ECF=135°.

所以△EFC≌△CPE.

所以EF=CP.

于是AB=EF.

4.旋转模型：利用有公共顶点的线段，构造旋转图形

利用已知条件，构造旋转图形，利用旋转变换的图形全等，对应边相等，获得有关证明.

证法7：如图7，连接AC，过点E作EP⊥BC，交AC于点P.

图7

因为∠ACB=∠CPE=45°，

所以EP=EC，

且∠APE=∠ECF=135°.

因为AB∥PE，

所以∠BAE=∠AEP.

又∠BAE=∠FEC，

于是∠AEP=∠FEC，

则△AEP≌△FEC.

所以AE=EF.

5.圆模型：利用线段同侧等角，构造四点共圆

利用线段同侧∠AEF=∠ACF这一条件，构造辅助圆，再利用圆的基本性质，证得同一个三角形的两内角相等，最后，利用等角对等边获得结论.

证法8：如图8，连接AC，AF.

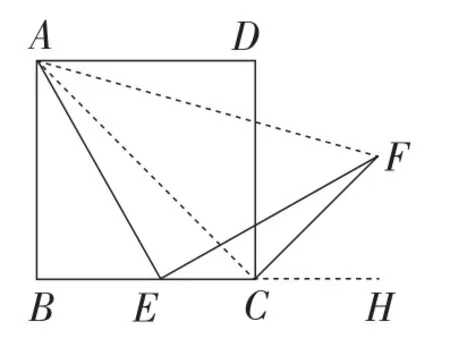
图8

因为四边形ABCD为正方形，

所以∠ACD=∠ACB=45°.

因为CF平分∠DCH.

所以∠DCF=45°.

所以∠ACF=∠ACD+∠DCF=90°.

又∠AEF=90°.

所以A，E，C，F四点共圆.

所以∠EFA=∠ACE=45°.

在Rt△AEF中，∠EAF=90°-∠EFA=45°，

所以∠EAF=∠AFE=45°.

则AE=EF.

二、同类试题探究

题有千变万化，但万变不离其宗，“宗”即为教材知识和方法体现的基本数学模型.《义务教育数学课程标准（2011年版）》指出，模型思想的建立是学生体会和理解数学与外部世界联系的基本途径，数学模型是一种常见的解决问题的思考方法.

例1（2015年浙江·温州卷）如图9，AB是半圆O的直径，CD⊥AB于点C，交半圆于点E，DF切半圆于点F．已知∠AEF=135°．

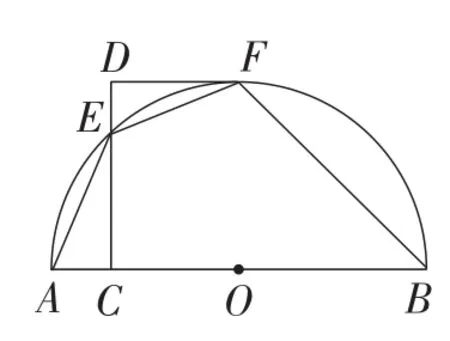
图9

（1）求证：DF∥AB；

解析：（1）如图10，连接OF，利用切线的性质模型，得∠DFO=90°.再根据圆内接四边形的性质得到∠AEF+∠B=180°.由于∠AEF=135°，得出∠B=45°.于是得到∠AOF=2∠B=90°.根据同旁内角互补，两直线平行的判定，结论可证.

图10

图11

（2）如图11，连接OE，OF，由第（1）小题得∠AOF=∠FOB=90°，且BF=OF=OB.由勾股定理可得OF=OB=2.又因为OC=CE，CD⊥AB，OE=OF=2，所以由四边形DCOF是矩形，得CD=OF=2.所以DE=2-

例2（2015年湖北·武汉卷）如图12，△ABC，△EFG均是边长为2的等边三角形，D是边BC，EF的中点，直线AG，FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是（）.

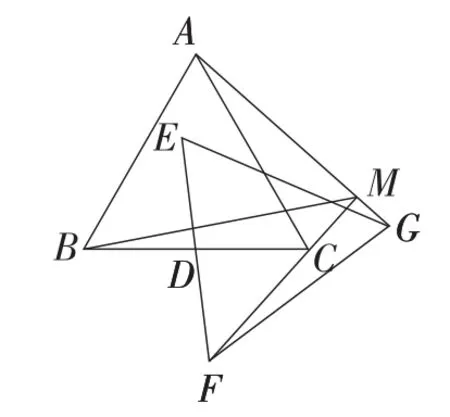
图12

图13

解析：如图13，连接AD，DG.根据旋转角相等，旋转前后的对应线段相等，容易发现∠ADG=∠FDC，DA=DG，DF=DC，故∠DFC=∠DCF=∠DAG=∠DGA.又根据等腰三角形的“三线合一”，可知∠FDG=90°，所以∠DFG+∠DGF=90°，即∠DFC+∠CFG+∠DGF=90°.所以∠AMC=∠MGF+∠CFG=∠DGA+∠DGF+∠CFG=∠DFC+∠DGF+∠CFG=90°.故点M始终在以AC为直径的圆上，作出该圆，设圆心为点O，连接BO，与⊙O相交于点P，线段BP的长即为线段BM长的最小值.得B故此题选D.

借助旋转的性质找出解题思路是分析有关旋转问题的重要方法.

事实上，每一道几何题目背后都有着一定的法则和规律，每一类题都有着相似的解题思想，这种思想的集中体现，便是模型.模型有形似、神似、融汇之分，难度由浅入深，可以通过多总结，多应用，深思考，来熟悉不同模型的解题思路和方法，按照模型并根据图形特点思考解法.通过一题多解、拓展变式发现模型之间的相互关系，增强自己对模型的理解深度，为几何学习和运用添彩增效.有效利用模型的概括性和对解题思路的启发作用，促进学生有效解题.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］王尧兴.几何图形中利用基本模型解题例析［J］.理科考试研究，2014（9）：1-2.

2016—08—18

李发勇（1964—），男，中学高级教师，主要从事初中数学教材、教学、解题及命题研究.