制作容积尽可能大的长方体纸盒——一节市级数学实验研讨课的教学叙事与反思

姜晓刚（江苏省连云港市新海实验中学教育集团）

制作容积尽可能大的长方体纸盒
——一节市级数学实验研讨课的教学叙事与反思

姜晓刚（江苏省连云港市新海实验中学教育集团）

以一节市级九年级数学实验教学研讨课“制作容积尽可能大的长方体纸盒”为例，以数学实验教学为视角，叙述教学中的平淡与精彩，预设与生成，交流与碰撞，思考与反思，让学生在“做”中思考，在“做”中发现，在“做”中感悟，积极地投身于课堂探究和发现之中．

数学实验；教学叙事；长方体纸盒

2015年4月，受市级立项课题“初中数学实验教学的实践研究”课题组的委托，以及市初中数学青年教师训练营的邀请，结合九年级的复习进度，笔者开设了一节数学实验教学研讨课“制作容积尽可能大的长方体纸盒”，反响颇为热烈．现将教学叙事与反思呈现出来，与广大同仁交流分享．

一、教学叙事

学情分析：九年级在计划复习“图形与几何”中的展开与折叠的相关内容时，学生已经完成第三学段数学知识内容的学习，形成了一定的空间观念、数感及符号感，学会了用字母表示数，会初步应用统计知识来描述事物的特性，等等．加之七年级时都经历了“制作无盖的长方体纸盒”的探究学习，感受“从实际问题抽象出数学问题—建立数学模型—综合应用已有的知识解决问题”的过程.为了体现数学实验教学的特点，体会知识点之间的联系，拟让学生制作容积尽可能大的长方体纸盒，再次经历想象、实验、分析、猜测、交流、推理和反思等一系列过程，综合图形的展开与折叠、字母表示数，以及用代数式的值去推断代数式所反映的规律，从而提高学生综合运用知识的能力．

教学目标：经历观察、猜测、实验、抽象、交流、合作、推理与反思等一系列活动，综合图形的展开与折叠、字母表示数，以及用代数式的值去推断代数式所反映的规律，再次感受“从实际问题抽象出数学问题—建立数学模型—综合应用已有的知识解决问题”的过程，进一步丰富空间观念与符号感，发展推理能力，获得一些研究问题的方法和经验．

教学重点：引导学生探索如何设计并制作长方体纸盒.

教学难点：引导学生探索如何设计并制作容积尽可能大的长方体纸盒.

课前准备：边长为20cm的正方形纸片，剪刀．

教学过程：

1.回顾，温习

（1）用一张边长为a的正方形纸片（如图1（1）），在其四个角上剪去四个边长为b的小正方形，可以制成一个无盖的长方体纸盒，如图1（2）所示．

图1

（2）正方体的平面展开图有11种（如图2）：中间四个面，上下各一面；中间三个面，一二隔河见；中间二个面，楼梯天天见；中间没有面，三三连一线．

图2

【设计意图】通过直观地呈现，唤醒学生相关知识点的回忆，为下面的图形设计和实验操作做出铺垫．

2.制作，计算

师：请同学们拿出一张20cm的正方形纸片，经过适当裁剪，将剩余部分（必须是一张纸面）拼合成长方体密闭纸盒，而且使得该密闭纸盒的容积尽可能的大．

【设计意图】呈现言简意赅、指向明确的问题后，立即将学生置身于一个非常有趣的、富有挑战性的问题情境中去．这样的实验教学犹如“一石激起千层浪”，课堂顿时热闹了起来.学生对这个问题的发生、发展过程始终抱有好奇心和强烈的求知欲，各学习小组都积极投入到探索解决问题之中．学生自己动手实验、观察、比较、归纳，亲自经历数学知识的发现过程，体现了数学实验以教师为主导、以学生为主体的教学原则．

（1）有序进行.

教学中，学生最先也是最多地提供了如图3所示的解决方案（中间四个面，上下各一面），而且容易看出4a=20，得a=5.进而得到正方体纸盒的容积为125cm3．不多时，有一名学生将图3裁剪后的纸片斜放在20cm的正方形纸片上，发现“剩下的部分”很宽裕，显然可将图3中的纸片整体放大点，于是产生了如图4所示的解决方案.在图4中，BC=由所以此时纸盒的容积为显然此时的容积较大．

图3

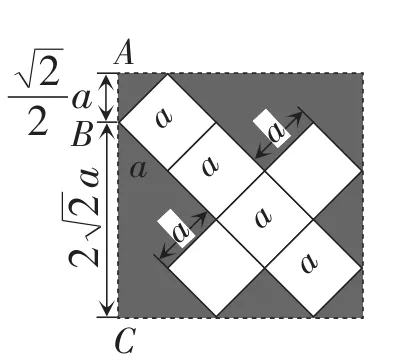
图4

（2）意外的精彩.

计算刚罢，生1立刻举手，说自己在20cm正方形纸片上画出来的纸盒的容积更大，并将如图5所示的图形展示给大家看，其同桌瞄一眼并提醒道：你的盒子没有盖子！随即引发一片笑声，生1局促不安地坐了下去．

师：生1爱动脑筋值得肯定，要是能再细心些就会更好.

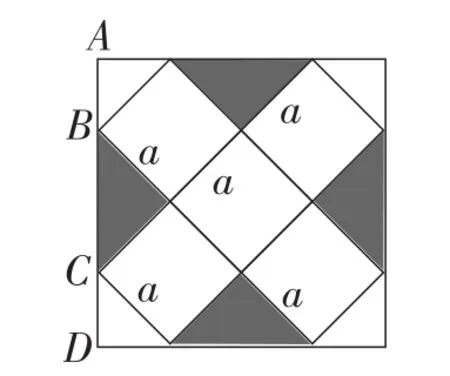
图5

图6

由于笔者之前研究了按照图6的裁剪完全可以拼合成如图7所示的正方体，本想留待本节课压轴奉献，不料此处需要，只好提前救急出场．

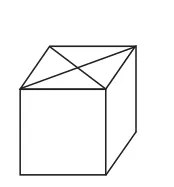
图7

师：别人不经意或不成熟的想法也许会给我们以启发和指引.生1的方案（如图5）显然缺少一个面，但是将该方案稍加修改，一定让你眼界大开，脑洞大开．

笔者拿出了事先准备好的纸片（如图6），让全体学生一起制图、裁剪（减去虚线和阴影），然后尝试拼合．

因为在学生（甚至教师）的认识中，拼合的每个面都是完整的长（正）方形，哪曾想到面也可以拼合.此处笔者没有让学生去进行不着边际的尝试，而是让学生直接跟着教师，不是创造精彩，而是欣赏精彩．

一个学生拼成、二个学生拼成、……，学生都喜形于色，啧啧称奇.

师：从图3的方案，到图4的方案，再到图6的方案，计算的结果可清晰表明，所制作出的三个正方体的体积是逐渐增大的.其实不用计算，也可以明显感觉到单个面上的正方形的面积是逐渐增大的．

生2：其实最大的正方体，制作时被剪裁的纸片的面积是最少的．

生3：剪去的少，剩下的多，所以单个面的面积就大.

生4：剪去的少，制作成的立方体的体积就应该大．

生5：这三个都是正方体，可是课题是：制作容积尽可能大的长方体呀？

生6：正方体是特殊的长方体，不矛盾.

……

师：大家众说纷纭，各有各的见解，但对不对呢？实践是检验真理的唯一标准.

（4）合力逼近.

学生纷纷在20cm的正方形纸片上规划起来.笔者巡视过程中，选择了两名学生的设计图（如图8，图9）投影到幕布上，并在图形上进行了适当的标注．

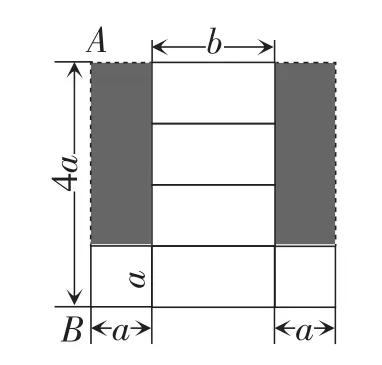
图8

图9

在图8的方案中，4a=20，得a=5；2a+b=20，得b=10.所以拼合成的长方体的体积为a2b=250．

在图9的方案中，由2a+2b=20，得a+b=10，即a=10-b；由2b+c=20，得c=20-2b.所以拼合成的长方体的体积为abc=b（10-b）（20-2b）

这个体积怎么算，居然是三次函数，大家都愣住了．

师：从图9中可以看出，b的取值在0至10之间，下面我们分工合作进行计算，第一小组取b=1，……，第九小组取b=9，分别代入计算.老师嘛，就吃点亏，取b=0和b=10代入计算.看哪个小组算得快和对．

不一会儿，各小组派代表依次说出计算结果并填入表1.

表1

师：大家观察表1，有什么发现？

生7：当b=3时，体积的值最大，为294．

师：还有呢？

生8：随着b的增大，体积先变大，再变小．

师：我们再进行一轮计算：第一小组取b=2.5，……，第五小组取b=2.9，第六小组取b=3.1，……，第九小组取b=3.4，分别代入计算，老师取b=3.5代入计算.看哪个小组算得即快又对．

过一会儿，得表2.

表2

师：大家观察表2，又有什么发现？

生9：当b=3.3时，体积的值最大，为296.27cm3．

生10：老师，这个方法好像叫逼近法.下面应该在3.3左右取值再去计算，就这样算下去，对吧？

师：姑且就认为按照如图9所示的方法制作拼合而成的长方体的容积296.27cm3为最大值．

（5）再现精彩.

生11急切地举手，兴奋地展示出了一种巧妙的方案，如图10所示．

图10

师：这简直是赤裸裸地侵犯图6方案的知识产权，建议此处应该有掌声.

此时下课铃响了.

师：如何求出此时长方体的容积的最大值就作为课外作业了.

注：用逼近法可求出此时最大容积为417.6cm3.

下课！

（6）追记补遗.

几天后，有两名学生向笔者提供了如图11所示的裁剪方案，折合成长方体后，其中的两个对面如图12所示.问及最大的容积是多少，竟说还没有来得及想.

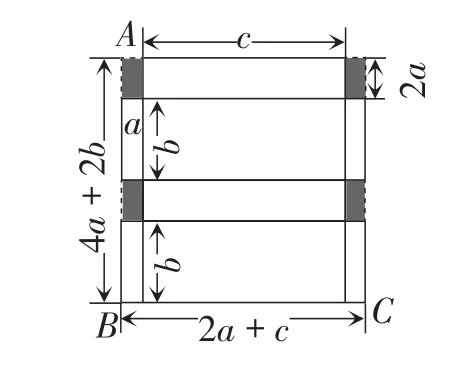
图11

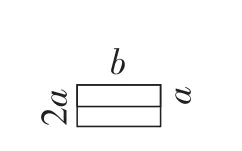
图12

注：精彩地欣赏之后往往会有模仿或创新的冲动．图11可以看作是在图9方案的基础上运用图6拼合成侧面的思想方法而成，有所创新.而拼合的长方体的最大体积，可以类似地用数学逼近的方法求得，数值为384.8cm3.

给学生一碗水，教师就得有一桶水.经过几日的查询、思考和操作，在图6的基础上经改良得到如图13所示的剪裁方案，其中的一个拼合的面如图14所示．正当为自己的方案欣喜不久，一个巨大的困难横亘于眼前：如何计算此时长方体的最大容积？

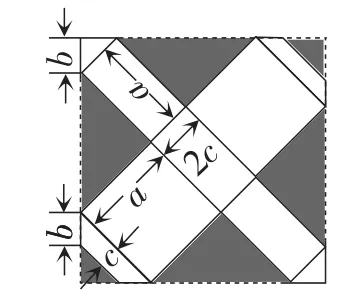
图13

图14

该方案中体积也可以表示为一个二元三次函数，但两个变量之间满足的是不等关系，给用逼近法求最大值增加了许多“变数”，无奈只好借助于计算机编程，利用计算机，近似地得出图13的裁剪拼出的最大的容积为397.6cm3.

在师生共同探究的八种剪拼方案中，以图10的方案剪拼成的密闭长方体的容积最大，数值为417.6cm3；以图3的方案剪拼成的密闭长方体的容积最小，数值为125cm3.貌似剪去的少，剩下的多，所以剪拼成的长方体的容积就应该大，但图10的方案中减去的纸片面积为44.4cm2，而图11的的方案中减去的纸片面积为35.6cm2，这可是一个鲜活的反例呀.

二、教后反思

数学实验教学是以《义务教育数学课程标准（2011年版）》（以下简称《标准》）基本理念为指导，为实现初中阶段数学课程目标，以实现初中数学的课程目标为教学目标，根据初中数学知识内容特点和学生学习心理等特点，组织指导学生借助有关工具（如纸张、剪刀、模型、测量工具、制图工具及计算机等）进行动手操作，使学生在观察、思考、分析、归纳等活动中体验数学知识的发生、发展及形成的过程，同时也经历情感体验、进行潜能开发的师生活动．

1.选准数学实验教学的起点

实验教学起点太低，学生会觉得没有探究的必要，不能激发学生探究的兴趣；起点太高，学生无法在已有的知识方法与所要探究的对象之间建立有效的联系，从而失去探究的欲望．本节课教学起点建立在七年级的课题“制作无盖的长方体纸盒”的学习之上，借助于后续的数学知识和思想方法所进行的实验探究，从无盖到有盖、从折叠到计算、从常规到创新，拾级而上，自然而然，避免了曲高和寡的尴尬．

2.注重数学思想方法的渗透

数学实验教学中，应注重加强学生在逐步解决问题的过程中体会与感悟其中所蕴涵的数学思想与方法.通过数学实验的直观，努力使研究的内容可视化，让学生从中获得对数与形的理解，并逐步对其适度抽象，进行更高层次上的再实验，进而体会数学的研究方法，使学生在活动中认识并改造自己的数学知识结构．本节课学生很自如地运用化立体为平面、数学逼近、相似放大、图形割补、数形结合等思想方法到解决问题之中．

3.突出教师的主导协调与学生的主体参与

《标准》指出，学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者．数学实验教学中教师要引导学生经历“做数学”的过程，给予学生平等交流和恰当的指导，关键在于给学生提供适当的问题情境，营造一个激励探索和促进理解的氛围，为学生提供富有启发性的交流环境.数学实验教学中教师要鼓励学生大胆表达，在加深理解的基础上，对不同的答案进行交流讨论，还要引导学生分享彼此的思想和结果，并重新审视自己的看法和结果.教师还要善于捕捉学生的想法，及时恰当地启发学生关注问题的重要方面，适时指导学生对出现在学习过程中的有意义的现象进行归纳、总结，促使学生思考和寻找眼前的问题与自己已有的知识体验之间的联系，让学生的操作、交流和思考有意义，有价值．

学生主体参与是数学实验教学最明显、最本质的特征，让学生自主经历动手操作、探究、发现、思考、分析、归纳等活动，充分调动学生学习的积极性，让学生由“要我做实验”转变成“我要做实验”，其主体作用和地位得以充分发挥，才能达到实验教学的目的．数学实验教学，由于受教学时间和大多数学生水平能力的限制，课堂上不可能探究得太深入，但数学实验能唤醒学生的主体意识，激发学生的好奇心和兴趣，课后还可以引导学生进行更深入的研究，让学生真正理解数学的本质，体会数学知识的博大精深和相互联系，形成新的数学模型.

4.关注数学基本活动经验的获取和积累

张奠宙教授认为，数学教学是数学活动的教学，学生在无处不在的数学活动中获得数学经验，与数学基本知识、基本能力、基本思想方法交织在一起，渗透在整个数学学习过程之中．

数学基本活动经验的获得要在好的数学实验活动当中，教师悉心准备和策划数学实验活动是使学生获取数学活动经验的核心．教师设计的数学活动应以学生的数学认知规律为基础，应该能为学生提供更多的探索空间，能够充分发挥学生的主体性，使学生积极主动地参与和体验．例如，本节课中，学生在解决问题时从简单到复杂、从操作到计算、从模仿到创造、从课内到课外，在“做”中思维，在“做”中发现，在“做”中感悟，积极地投身于数学探究和发现之中．整个活动的亲历和问题解决的经历，对学生数学基本活动经验的获取和积累大有裨益．

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］邬云德.寓“过程教育”于“认识不等式”教学探索及反思［J］.中国数学教育（初中版），2014（1/2）：68-70.

［4］孙立章.一堂数学实验课的思考［J］.中学数学（初中版），2015（6）:59－60．

2016—08—24

姜晓刚（1970—），男，中学高级教师，主要从事数学实验教学的设计与实施的研究.