基于弱测量的量子失协
2016-12-23郝小宁
郝小宁
(太原理工大学 数学学院, 山西 太原 030024)
基于弱测量的量子失协
郝小宁
(太原理工大学 数学学院, 山西 太原 030024)
探讨了量子信息理论中基于弱测量的量子失协的相关问题, 证明了主要结论: 令希尔伯特空间H=HA⊗HB, dimHA=n(2 乘积态; 弱测量; 超量子失协; 互信息; 量子失协 描述和量化量子关联是量子信息科学的一个基本和关键的问题[1]. 许多学者对量子关联的不同度量进行了研究, 例如量子失协、几何失协[2]以及量子亏损[3]等. 量子失协表示通过测量单个子系统不能被提取的不可达信息. 它是度量总的关联与经典关联之间的差[4]. 可分态的纠缠是零, 但是它们的量子失协可以是非零的[5]. 这表明除量子纠缠外, 量子失协可以反映量子态更多的量子关联. 量子失协能有效地反映量子关联的作用, 这不同于经典关联. 因此, 量子失协引起广大学者的关注并进行深入研究. Xi Zhengjun等学者给出两体态的量子失协的上界[6]. Luo Shunlong给出two-qubit系统量子失协的解析公式[7]. Mohamed给出two-qubit态的量子失协的动力学相关研究[8]. 在量子力学中, 量子测量起着非常重要的作用. 量子态对量子测量是非常敏感的. 对量子态进行测量不可避免地要扰动量子系统, 进而产生波函数的塌缩. 为使对初始量子态的影响最小, Oreshov 和Brun提出弱测量的理论以及弱测量算子的形式[9-10]. 弱测量不仅在研究基本的物理问题中, 而且在技术应用中都起着很重要的作用. 基于弱测量并结合量子失协Singh 和Pati 提出超量子失协(SQD)[11], 并证明在一个子系统上进行弱测量能使得SQD总是大于等于由投影测量得到的一般的量子失协(QD)[11]. 随后, 李波等学者对two-qubit的SQD、QD和互信息进行研究[12]. 同时, 基于弱测量[13-14], 一些学者也进行了相关研究. Zhang Jun等学者在弱测量下研究量子关联的花费[15]. Wang Yaokun等学者基于弱测量给出最大的holevo量[16]. Li Tao等学者对two-qubit的X型态给出超量子失协的解析公式[17], 也即给出低维系统的超量子失协的解析公式. Li Lei等学者研究弱测量下的量子失协的几何测量[18]. 我们知道, 对于两体的高维系统可以提高量子信息处理的效率[19]. 而先前学者们的研究并没有对高维系统的QD, SQD, 乘积态, 经典关联以及互信息的关系进行研究. 因此, 本文主要工作是基于弱测量研究在高维量子系统的量子失协的相关问题, 给出乘积态, 超量子失协, 量子失协, 经典关联和互信息之间等价命题的刻画. 这个结果是参考文献[12]中two-qubit情形在高维的推广. 下面介绍本文的一些基本概念及符号表示.HA和HB是Hilbert空间, dimHA=n(2 D(ρ)=I(ρ)-C(ρ)= S=(A|ΠB)= D(ρ)= S(A|B), n⊗2(2≤n<∞)量子系统上超量子失协Dw(ρ)的定义[11]为 |PB(x)}-S(A|B), 其中, 条件熵S(A|B)=S(ρ)-S(ρB), 并且 Sw{A|PB(x)}= p(+x)S(ρA|PB(+x))+p(-x)S(ρA|PB(-x)), 测后的态 ρA|PB(±x)= 概率 p(±x)= Tr{IA⊗PB(±x))ρ(IA⊗PB(±x))}, 注意 PB(+x)=απ1+βπ2, PB(-x)=βπ1+απ2, p(x)+p(-x)=1, π1+π2=PB(+x)+PB(+x)+ PB(-x)+PB(-x)=I, 式中: x是测量强度的参数. 引理 1 令H=HA⊗HB,dimH<∞, ρ∈S(H), C(ρ)=0当且仅当ρ是一个乘积态, 即ρ=ρA⊗ρB[12]. 基于引理1, 李波等学者给出下列定理 1. 定理 1 对two-qubit态, 下列7个陈述是等价的: 1) ρ是一个乘积态. 2) ρ有零经典关联. 3) ρ有零超量子失协. 4) ρ有零互信息. 5) ρ有相等的量子失协与超量子失协. 6) ρ有相等的量子失协和互信息. 7) ρ有相等的超量子失协和互信息. 这里先介绍m(2 HA和HB是希尔伯特空间, dimHA=n(2 dimHB=m(2 对n⊗m量子系统, 超量子失协的定义是 |M(x)}-S(A|B), 其中, 条件熵S(A|B)=S(ρ)-S(ρB), 并且 测量后子系统A上的态是 相应的概率分别为 所以, 定理 2 令H=HA⊗HB, dimHA=n(2 1) ρ是乘积态, 即ρ=ρA⊗ρB. 2) ρ有零超量子失协. 3) ρ有相等的量子失协和超量子失协. 4) ρ有零互信息. 5) ρ有相等的量子失协和互信息. 6) ρ有相等的超量子失协和互信息. 证明 1)⟹2). 由陈述1), 可得 TrB{[I⊗M1(x)](ρA⊗ρB)[I⊗M1(x)]}= p1(x)= TrAB{[I⊗M1(x)](ρA⊗ρB)[I⊗M1(x)]}= 所以, 2)⟹3), 4)⟹5)以及5)⟹6)的证明方法与定理1的证明相似. 3)⟹4). 弱量子条件熵是 Sw{A|MB(x)}= 注意, 弱量子条件熵 Sw{A|MB(x)}=Sw{A| 其中, Sw{A|MB(x)}= 这表明C(ρ)=0, 由引理1可知ρ是一个乘积态,I(ρ)=0. 因此, 陈述4)成立. 6)⟹1). 由式(2), von Neumann熵的凹性及陈述6), 可以得到 [1]Henderson L, Vedral V. Classical, quantum and total correlations[J]. J. Phys. A, 2001, 34(35): 6899-6905. [2]Li Bo, Wang Zhixi, Fei Shaoming. Quantum discord and geometry for a class of two-qubit states[J]. Phys. Rev. A, 2011, 83(2): 1293-1304. [3]Xi Zhengjun, Fan Heng, Li Yongming.One-way unlocalizable quantum discord[J]. Phys. Rev. A, 2012, 85(5): 1222-1228. [4]Ollivier H, Zurek W H. Quantum Discord: A measure of the quantumness of correlations[J]. Phys. Rev. Lett, 2002, 88(1): 017901. [5]Horodecki R, Horodecki P, Horodecki M, et al. Quantum entanglement[J]. Rev. Mod. Phys. 2007, 81(2): 865-942. [6]Xi Zhengjun, Lu Xiaoming, Wang Xiaoguang, et al. Necessary and sufficient condition for saturating the upper bound of quantum discord[J]. Phys. Rev. A, 2012, 85(3): 2371-2376. [7]Luo Shunlong. Quantum discord for two-qubit systems[J]. Phys. Rev. A, 2008, 77(4): 140. [8]Mohamed A B A. Quantum discord and its geometric measure with death entanglement in correlated dephasing two qubits system[J]. Quant. Inf. Rev, 2013, 1(1): 1-7. [9]Aharonov Y, Albert D Z, Vaidman L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100[J]. Phys. Rev. Lett, 1988, 60(14): 1351-1354. [10]Oreshkov O, Brun T A. Weak measurements are universal[J]. Phys. Rev. Lett, 2005, 95(11): 110409. [11]Singh U, Pati A K. Quantum discord with weak measurements[J]. Ann. Phys, 2014, 343(4): 141-152. [12]Li Bo, Chen Lin, Fan Heng. Non-zero total correlation means non-zero quantum correlation[J]. Phys. Lett. A. 2014, 378(18-19): 1249-1253. [13]Hu Mingliang, Fan Heng, Tian Dongping. Role of weak measurements on states ordering and monogamy of quantum correlation[J]. Int. J. Theor. Phys, 2014, 54(1): 1-10. [14]Wang Yaokun, Ma Teng, Fan Heng, et al. Super-quantum correlation and geometry for Bell-diagonal states with weak measurements[J]. Quantum Inf Process, 2014, 13(2): 283-297. [15]Zhang Jun, Wu Shaoxiong, Yu Changshui. Quantum correlation cost of the weak measurement[J]. Ann. Phys, 2014, 351: 104-111. [16]Wang Yaokun, Fei Shaoming, Wang Zhixi, et al. Maximal holevo quantity based on weak measurements[J]. Sci. Rep, 2015, 5: 10727. [17]Li Tao, Ma Teng, Wang Yaokun, et al. Super Quantum discord for X-type states[J]. Int. J. Theor. Phys, 2015, 54(2): 680-688. [18]Li Lei,Wang Qingwen, Shen Shuqian, et al. Geometric measure of quantum discord with weak measurements[J]. Quantum Inf Process, 2015, 15(1): 291-300. [19]Walborn S P, Lemelle D S, Almeida M P, et al. Quantum key distribution with higher-order alphabets using spatially encoded qudits[J]. Phys. Rev. Lett, 2006, 96(9): 090501. Quantum Discord Based on Weak Measurements HAO Xiao-ning (College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China) An exploration was made on the relevant issue of quantum discord in quantum information field. Let Hilbert space to beH=HA⊗HB, dimHA=n(2 product state; weak measurements; super quantum discord; mutual information; quantum discord 1673-3193(2016)06-0566-04 2016-03-31 国家自然科学基金资助项目(11171249);山西省国际合作项目(2014081027-2);太原理工大学青年基金资助项目(2014QN024) 郝小宁(1980-), 女, 博士, 讲师, 主要从事算子及量子信息与量子计算研究. O413 A 10.3969/j.issn.1673-3193.2016.06.0031 预备知识




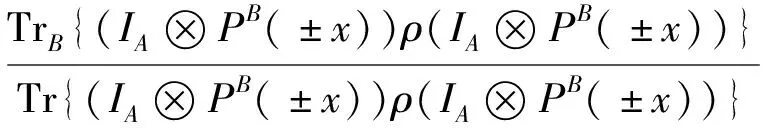
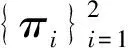
2 主要结果