基于分布式压缩感知的信道估计导频优化策略*

2016-12-22赖鑫琳陈忠辉赵宜升

电子技术应用 2016年12期

关键词：导频图样信道

赖鑫琳，陈忠辉，赵宜升

（福州大学物理与信息工程学院，福建福州 350108）

基于分布式压缩感知的信道估计导频优化策略*

赖鑫琳，陈忠辉，赵宜升

（福州大学物理与信息工程学院，福建福州 350108）

为了保证为LTE-R系统用户提供可靠的无线通信服务，需要通过信道估计获取信道状态信息。在高速移动性场景下，无线信道呈现频率-时间双选择性，若要实现信道估计，则需引入大量导频。针对上述问题，提出一种结合分布式压缩感知理论的信道估计导频优化方案。首先，根据时延域中无线信道的稀疏特性挖掘基函数系数之间的联合稀疏性并对估计方程进行去耦处理。接着，引入分布式压缩感知理论，获得一种能够抑制子载波间干扰的新型导频图样。仿真结果表明，对导频图样的优化处理，可使信道估计方案的系统性能显著优于传统方案。

分布式压缩感知；信道估计；频率-时间双选择性；联合稀疏性

0 引言

对于新一代铁路长期演进（Long Term Evolution for Railway，LTE-R）系统，列车移动速度超过 300 km/h，无线信道呈现频率-时间双选择性，产生严重的子载波间干扰（Inter-Carrier Interference，ICI），系统性能被严重恶化。通过信道估计来获得信道状态信息，能够显著提高通信系统性能。因此，针对LTE-R系统，开展信道估计研究具有重要意义。

近年来，随着对无线信道的深入研究，人们发现，多径的数量一般远大于10，但其中大部分路径的能量为零或约等于零，仅少量路径携带着不可忽略的能量[1]，这体现了无线信道的稀疏性质。若继续采用传统信道估计方案[2]，需引入大量导频，引起频带资源的浪费。压缩感知(Compressive Sensing，CS)技术能够从较少的观测样本中重构稀疏信号[3]，为在信道估计策略中减少导频数目提供了可行的解决方案。在文献[4]中，针对具有频率选择性的稀疏信道，作者引入了CS理论，有效减少了导频数目。TAUBOCK G等人研究了双选择性信道在时延-多普勒频域的稀疏性，并结合CS理论研究信道估计问题[5]。分布式压缩感知（Distributed Compressive Sensing，DCS）能够解决在相同场景下，CS效率较低的问题[6]。DCS通过挖掘待估计信号的共同稀疏性，意图联合重构这些稀疏信号[6]。

针对LTE-R系统，本文提出一种基于DCS的信道估计导频优化方案。首先，本文采用复指数基扩展模型（Complex-Exponential Basis Expansion Model，CE-BEM）建模无线信道，并根据无线宽带信道在时延域中的稀疏性[7]，证明了基函数系数之间的联合稀疏性。接着，对估计方程进行去耦操作，再利用DCS理论获得能够抑制ICI的新型导频图样。最后，本文通过仿真对传统方案、CS方案与DCS方案的归一化均方误差进行对比。

1 系统模型与DCS理论

1.1 LTE-R通信场景

本文所研究的高速铁路通信场景如图1所示。一般的移动通信系统采用面状覆盖，而高速铁路通信系统采用带状覆盖。高速铁路专网的拓扑结构是由基带处理单元（Building Baseband Unit，BBU）和射频拉远单元（Radio Remote Unit，RRU）组成。一个BBU分别与多个 RRU通过光纤相连接，多个RRU连续等距地部署在高速铁路沿线。每辆列车的第一节车厢配置了一个车载接收设备（Vehicular Station，VS），用于接收来自RRU的射频信号。VS利用电缆以及每节车厢所配置的中继器（Repeater，R）将所接收到的信号传递至每节车厢的用户设备（User Equipments，UE）。本文需要实现的是对RRU与VS之间的无线信道的估计。在高速移动场景下，该无线信道呈现频率-时间双选择性。

图1 LTE-R通信系统的网络结构

正交频分复用（Orthogonal Frequency-Division Multiplexing，OFDM）是LTE-R系统的关键技术之一。在OFDM系统中，传输一个OFDM符号需要N个子载波：X≜(X[0]，…，X[N-1])T。信号传输之前，需对其进行 N点快速傅里叶逆变换，得时域信号x=(x[0]，…，x[N-1])T。为了有效抑制符号间干扰（Inter Symbol Interference，ISI），需对发送端信号x添加循环前缀，并在接收端去除该循环前缀，则接收端时域信号可表示为：y=Hx+w=(y[0]，…，y[N-1])T。时域信道传输矩阵 H∈CN×N（即H为 N×N维矩阵）呈类循环移位矩阵的构造[2]。在接收端，经快速傅里叶变换得：Y=Fy=FHFHX+Fw，Y=(Y[0]，…，Y[N-1])T为频域接收信号，w为噪声信号。F为标准归一化傅里叶变换矩阵。

1.2 DCS理论

CS技术指利用数量有限的测量值来准确重构稀疏信号。若利用CS重构向量m=(m[0]，…，m[N-1])T，即求解：

其中，Φ∈CG×N为已知测量矩阵；n∈CG×1代表 G(G＜＜N)个测量值；v为噪声向量，且m中仅有K个非零值。定义矩阵的互相关性（Mutual Coherence Property，MCP）[6]：矩阵Φ∈CG×N的互相关性被定义为：

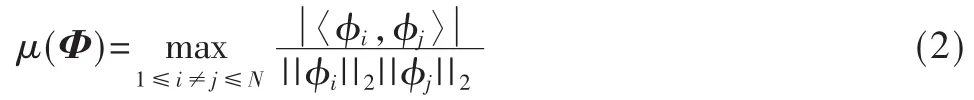
若 μ(Φ)越小，越能准确重构 m[6]。DCS来源于多个信号同时稀疏时的CS。考虑一组含有Z个未知向量的问题：

其中，nz∈CG×1、vz∈CG×1且 mz∈CN×1。如上，每个 mz都是通过满足MCP的测量矩阵Φ进行重构的。此时，每个mz是否具有相同的稀疏性变得至关重要，不仅要求每个mz的零范数值都为K，还要求每个mz中所有非零元素所在的位置是完全一致的。构造矩阵，则有：

2 估计问题建模

2.1 基扩展模型

在一个OFDM符号时间内，第l(0≤l≤L-1)个信道抽头的冲激响应为：hl=(h[0，l]，…，h[N-1，l])T，h[n，l]为第n时刻、第l径的冲激响应。若用基扩展模型（Basis Expansion Model，BEM）拟合该信道抽头，即：

其中，B=[b0，…，bQ-1]；bq=(b[0，q]，…，b[N-1，q])T为第q (0≤q≤Q-1)个基函数；为第q个基函数、第l径的 BEM系数。接着，定义：h=[h0，…，hL-1]与c=[c0，…，cL-1]，则有：

信道估计方程可表述为[2]：

其中，Dq=Fdiag{bq}FH，Δq=diag{FLcq}，矩阵 FL为 F的前L列。BEM将待估计参数的个数由NL降低到QL，即估计Q个BEM系数向量。CE-BEM不依赖于信道的统计特性，且其频域信道转移矩阵保持着严格的带状分布。因此，本文采用 CE-BEM拟合无线信道，其基函数为：

2.2 BEM系数的稀疏性

若无线信道只有 K(K＜＜L)个信道抽头(在相应位置Γ={lα0，lα1，…，lαK-1})具有较大的抽头系数，即 h[n，l]≠0 (l∈Γ)，其余抽头具有较小的抽头系数，以至于可忽略，即h[n，l]=0(l∉Γ)。这种在时延域中呈现K阶稀疏的无线信道，被称为稀疏信道。在具有较大频谱带宽的宽带传输系统中，无线信道通常呈现稀疏性[7]。因OFDM系统占用了较大的带宽，则L也较大。利用BEM建模无线信道，有效导频数目至少为QL，而实际应用中导频数目应尽量少。后续，本文将采用一种可进一步减少有效导频数目(由QL减至QG，且G＜＜L)的信道表述方式。

根据信道在时延域中的稀疏性，当l∉Γ时，h[n，l]= 0，则有：hl=0，l∉Γ。由于，可得：0。根据式(6)，可发现每个 bq所对应的cq都是一个 K阶稀疏向量，且中非零元素所在位置都完全一致，即证明了的联合稀疏性。从而考虑采用DCS技术联合重构。然而，在应用 DCS理论之前，必须适当处理以下两个方面问题：由于ICI严重限制了估计的精度，需降低其影响或对其进行抑制；为联合重构，需采用相同的满足MCP的测量矩阵Φ。

3 导频图样优化方案

假设导频总个数为P，导频位置集合为γ。导频由两部分组成：

(1)非零导频位置集合为：γeff={p0，…，pG-1}∈CG×1，且(0≤p0＜…＜pG-1≤N-1)，非零导频个数为 G(K＜G＜＜L)，则对应子载波为：。

(2)值为零的保护导频位置集合为 γzero，保护导频个数为：|γzero|=(2Q-2)G，第k组保护导频的位置为：γzero，k= {pk-Q+1，…，pk-1，pk+1，…，pk+Q-1}，对应子载波为：Pzero=[X]γzero=0。

其中，γ0表示 γeff中每个元素的值减(Q-1)/2。本文假设Q=3，导频子载波、数据子载波的分布情况如图2所示。

图2 新型导频图样

通过对式(7)的去耦处理，获得了不受 ICI影响的 Q个等式：

且满足：|pi-pj|≥2Q-1，i≠j。由于式(12)中的解具有相关性，想要同时获得最优情况下的 γeff与 Peff存在一定难度。为简化该最优化问题的求解，则假设：

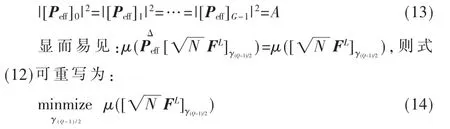
算法A基于DSO技术的导频图案设计算法步骤：

(1)初始化

随机生成一个满足|pi-pj|≥2Q-1，i≠j的导频图样，令当下最优导频图案为，[π]0= 0，[π]0，0=1，s=0，t=0。

(2)第n(n=0，1，…，MG)次迭代：

①生成另一种导频图案：

②比较对应矩阵的μ(*)：

③更新状态占用概率向量：

[π]n+1=[π]n+[δ]n+1([D]n+1-[π]n)，[δ]n=1/n。

④选择当下最优图案：

⑤n←n+1

(3)结束

4 仿真分析

在LTE-R通信系统中，基站沿着轨道部署。移动终端的发射信号经过无线信道到达接收端的过程中，传播路径将包含一条视距路径(Line-of-Sight，LOS)以及多条非视距路径(Non Line-of-Sight，NLOS)。因此，真实信道可以用莱斯衰落(Rician fading)信道模型来描述[10]。本文采用归一化均方误差(Normalized Mean Square Error，NMSE)来衡量估计精度：

图3比较了当 v=200 km/h时，传统方案、CS方案与DCS方案分别采用新导频图样与传统导频图样的估计精度。传统方案利用CE-BEM对信道进行建模(QCE=3)，采用等距梳状导频图样，并结合最小二乘(Least Squares，LS)估计准则，实现该信道估计[2]。仿真结果表明，将新型导频图样(μ1=0.25)应用于CS方案、DCS方案，随着系统信噪比的增加，能够较好地重构基函数系数，且能够获得一个相对较高的估计精度，明显优于采用传统导频图样(μ2=0.99)的CS方案、DCS方案。算法A通过寻求式(14)的最小值，获得了能够以最高概率重构BEM系数的最优导频图样。

图3 当v=200 km/h时，SNR与NMSE的关系

图4比较了当v=400 km/h时，传统方案、CS方案与DCS方案的系统性能。图5通过改变移动速度v，来比较3个方案的系统性能。传统方案的导频数目为P2= (2Q-1)L=5×32=160，其频带开销为 η2=62.5%，而CS方案与DCS方案的频带开销为η1=31.25%。从频带利用率的角度来看，CS方案与DCS方案能够大大减少导频开销。仿真结果表明，当SNR高于1 dB时，随着SNR的增加，DCS方案的估计精度能够明显高于传统方案，这是因为DCS方案对估计方程作了去耦处理，并采用了能够抑制ICI的新型导频图样。此外，由图4、图5可知，DCS方案的性能能够在一定程度上优于CS方案。这是因为DCS技术对数据共同处理的方法，提高了寻找未知信号非零元素位置的成功率。

图4 当 v=400 km/h时，SNR与NMSE的关系

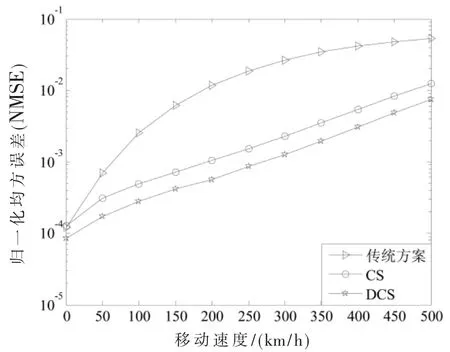
图5 当SNR=20 dB时，v与NMSE的关系

5 结论

本文研究了LTE-R通信系统中双选择性信道的信道估计导频优化问题。根据时延域中无线信道的稀疏性质，本文论证了BEM系数的联合稀疏性。接着，将估计方程转换为去耦形式，并引入DCS理论，以获取能够抑制ICI的最优导频图样。仿真结果表明，结合新型导频图样的DCS方案不仅能够提高传统方案的频谱利用率，还能够显著提高估计精度。当与CS方案具有相同数量的观测值时，DCS方案能够进一步提高估计精度。后续研究将把模型误差纳入考虑，以进一步优化估计方案。

[1]PAREDES J L，ARCE G R，WANG Z.Ultra-wideband compressed sensing：channel estimation[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(3)：383-395.

[2]TANG Z J，CANNIZZARO R C，LEUS G，et al.Pilotassisted time-varying channel estimation for OFDM systems[J].IEEE Transactions on Signal Processing，2007，55(5)：2226-2238.

[3]UNSER M.Sampling—50 years after Shannon[J].Proceedings of the IEEE，2000，88(4)：569-587.

[4]VUOKKO L，KOLMONEN V M，SALO J，et al.Measurement of large-scale cluster power characteristics for geometric channel models[J].IEEE Transactions on Antennas and Propagation，2007，55(11)：3361-3365.

[5]TAUBOCK G，HLAWATSCH F.A compressed sensing technique for OFDM channel estimation in mobile environments：exploiting channel sparsity for reducing pilots[C].Proceedings of IEEE International Conference on Acoustics.Las Vegas，America：IEEE Press，2008：2885-2888.

[6]DUARTE M F，ELDAR Y C.Structured compressed sensing：from theory to applications[J].IEEE Transactions on Signal Processing，2011，59(9)：4053-4085.

[7]RAGHAVAN V，SAYEED A M.Sublinear capacity scaling laws for sparse MIMO channels[J].IEEE Transactions on Information Theory，2011，57(1)：345-364.

[8]HOMEM-DE-MELLO T.Variable-sample methods for stochastic optimization[J].ACM Transactions on Modeling and Computer Simulation，2003，13(2)：108-133.

[9]TROPP J A，GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53(12)：4655-4666.

[10]BEAULIEU N C，CHEN Y.Maximum likelihood estimation of local average SNR in Ricean fading channels[J].IEEE Communications Letters，2005，9(3)：219-221.

Pilot optimization strategy of channel estimation based on distributed compressed sensing

Lai Xinlin，Chen Zhonghui，Zhao Yisheng
(College of Physics and Information Engineering，Fuzhou University，Fuzhou 350108，China)

In order to provide the users of long term evolution for railway(LTE-R)system with reliable wireless communication service,the channel state information need to be obtained by channel estimation.In high-speed mobility scenarios,the wireless channel is a time-frequency doubly-selective channel.In order to estimate the channel,a large number of pilots will be introduced.To tackle this problem,a pilot optimization strategy of channel estimation based on a distributed compressed sensing(DCS)method was proposed.First of all,according to the channel sparsity in the delay domain,the joint sparsity between basis function coefficients was excavated.And the estimating equation was decoupled.Then,a novel sparse pilot pattern based on the DCS theory which can remove inter-carrier interference was solved out.The simulation results show that the system performance of channel estimation strategy is significantly superior to the existing ones by the optimization of pilot pattern.

distributed compressed sensing；channel estimation；time-frequency doubly-selective；joint sparsity

TN92

10.16157/j.issn.0258-7998.2016.12.026

赖鑫琳，陈忠辉，赵宜升.基于分布式压缩感知的信道估计导频优化策略[J].电子技术应用，2016，42 (12)：100-104.

英文引用格式：Lai Xinlin，Chen Zhonghui，Zhao Yisheng.Pilot optimization strategy of channel estimation based on distributed compressed sensing[J].Application of Electronic Technique，2016，42(12)：100-104.

2016-05-24)

赖鑫琳（1992-），女，硕士研究生，主要研究方向：无线通信与网络、信道估计。

陈忠辉（1960-），通信作者，男，教授，主要研究方向：无线通信与网络、信道估计、数字信号处理，E-mail：czh@fzu.edu.cn。

赵宜升（1984-），男，博士，主要研究方向：无线通信与网络、信道估计、无线资源分配。

国家自然科学基金(U1405251)；福建省自然科学基金(2015J05122，2015J01250)