椭球颗粒随机紧密堆积实验研究

赵述敏,胡志刚

(西安交通大学理学院,710049,西安)



椭球颗粒随机紧密堆积实验研究

赵述敏,胡志刚

(西安交通大学理学院,710049,西安)

针对随机堆积问题在数理领域和实际生产中意义重大且目前尚无一般性的理论模型的问题,采用一种基于高分辨率工业X射线断层扫描(CT)无损检测的实验方法较精确地测定了椭球颗粒随机紧密堆积体系的3个重要参数,即堆积分数、取向序和配位数分布,结果表明,椭球纵横比为0.5左右时,堆积分数达到的最大值为74%,与现有的模拟结果一致,而在一定纵横比范围内,配位数的分布呈偏态分布,取向角与取向轴呈现出高对称性,但离散性较强,该结果与球体随机紧密堆积的差异较大。在不考虑摩擦刚体所需平均配位数为刚体自由度的2倍、有限堆积物的配位数分布满足古典的几何分布的2个假设下,提出了一种椭球的堆积理论,其能解释堆积参数的变化趋势。结论和实验手段对探讨非球体填充理论和计算堆积体孔隙率有一定的参考价值。

随机紧密堆积;堆积分数;配位数;取向序

颗粒物质的堆积问题已成为当前工程、材料等领域研究的热点之一,很多科学及工程都与堆积密切相关。数学上有关于堆积的著名Kepler猜想[1]和Hilbert第18问题已逐步得到解决,但距离堆积一般性理论还有一段距离;物理中液体、晶体和玻璃的微观结构[2]相态的转变会遇到堆积体系的处理问题。所以,堆积问题非常普遍,其中紧密堆积研究很有意义。有学者运用紧密堆积理论从统计角度研究了森林树木直径的分布[3],工程上利用颗粒紧密堆积对流可以显著提高换热效率[4]等。随机堆积体系的特征尚难以用解析的形式给出[5],利用相图分析[6]可以给出球体随机紧密堆积分数的极限,但无法提供配位数和取向序分布等其他重要的堆积参数,因此实验和计算机模拟成为研究随机紧密堆积体系的主要手段。Bernal实验研究了球体随机紧密堆积体系的特征,得到球体随机紧密堆积分数约为64%的结果[7]。球体的堆积算法相对容易实现[8],一些学者用不同的数值方法对非球体(如椭球)随机紧密堆积进行了研究。Donev等运用经过推广的Lubachevsky-Stillinger球堆积算法、通过分子动力学模拟的方法给出了椭球堆积分数Φ和配位数Z随纵横比α变化的曲线[9-10],李水乡等通过组合球模型、结合松弛算法给出了椭球随机紧密堆积的堆积分数[11],两者的趋势基本一致。近年来随机紧密填充实验均以椭球堆积为主[12-14]。Donev以M&M豆为样本,采用喷涂油漆干燥后对接触油漆痕迹计数的方法得到了配位数,但油漆会改变表面摩擦系数,对堆积体系产生较大的影响,且容易存在干燥不完全等问题;Schaller等通过X断层摄影和图像处理技术分析了紧密堆积椭球体系,但只局限于配位数的分析[15]。

为了克服上述实验的不足,同时尽量保留其中合理的部分,在合理选用椭球样本的情况下采用了工业X射线断层扫描(CT)无损检测方法。该方法对堆积体系基本无附加影响,且能较为准确地测定出5种纵横比的椭球随机紧密堆积体系的3个主要参数:堆积分数、取向序和配位数,实验结果与现有的仿真结果[9]基本一致。为了解释椭球随机紧密堆积的实验结果,在假定平均配位数和自由度的关系及配位数满足几何分布的情况下,导出了配位数分布和随机紧密堆积分数的表达式,以解释堆积参数的变化趋势。

1 CT无损检测和样本选择

工业CT成像是一种无损检测方法,其原理主要是不同密度的物质对X射线的线性吸收系数有所不同[16],根据透过样本的X射线的强度、结合CT重构算法,可以对扫描样本进行组织成像。本文使用了西安交通大学机械结构强度与振动国家重点实验室的工业CT设备,正常工作X射线管电压为500 kV,空间分辨率为20 μm。

实验中选取了5种椭球状有机玻璃珠子样本,如图1所示。为了简便起见,将这几种椭球样本视为旋转椭球,相对于一般的椭球,旋转椭球自由度较少,可以用纵横比(椭球纵轴b与横轴a之比)α唯一地表征。对于扁椭球,其特征轴为短半轴,α<1;对于长椭球,其特征轴为长半轴,α>1。椭球材料为有机玻璃,密度相对金属较小,且有足够的刚度,实验挤压后变形不超过2 μm,加工性好,沿特征轴钻孔方便,取向角的测量简单、可靠。有机玻璃珠子接近理想椭球,其偏差r/Δr≤0.01,样本的具体参数见表1。

2 实验方案

采取在一定高度下自然下落的方式实现颗粒在容器内的随机分布,同时完成一层堆积后适当摇晃容器,给颗粒施加一定压力,以保证紧密堆积。对堆积完成的堆积系统进行CT成像分析,可以得到堆积体系的3个重要参数(堆积分数、取向序和配位数)与纵横比的关系。

图1 5种纵横比的椭球样本

样本编号样本数2a/mm2b/mm2r/mmα12811750±002871±04705021911556±0251290±01108332031198±0391041741080±0151080±0292051481210±0133964±00733

2.1 随机紧密堆积分数

实验中同一纵横比的椭球颗粒之间的偏差在5%以内,这样可以认为样本中的椭球颗粒是全同的。用精确的排水方法验证得出,在全同下计算得到的椭球样本总体积与实际颗粒总体积相差1%左右,且计算简便,适用性更广,因此本文采用该方法计算。

堆积分数也称为致密度,堆积系统的堆积分数Φ定义为堆积颗粒总体积Vg占堆积容器体积Vc的比例,即

Φ=Vg/Vc

(1)

其中堆积颗粒总体积可以用椭球颗粒平均体积乘以总数来获得,堆积容器体积可以通过测量容器几何尺寸获得。

2.2 配位数

图2为实验中选取单元体和利用接触图样确定椭球颗粒配位数的过程。堆积体经扫描后重构出三维图像,其中单元体选自合适大小的包含选定的椭球颗粒。扫描平面从单元体底部向顶部移动,一旦存在接触点,则会在二维断面图中显示出来。从图2中的二维断面中可以清晰看出,椭球颗粒接触点有6个,表明这个椭球颗粒的配位数为6。

图2 单元体的选取及配位数的计数

2.3 取向序

采用高分子及液晶中常用的取向序定义,利用cosθ的二阶Legendre多项式作为取向序S的描述[17],则有

(2)

式中:θ为取向角,即椭球特征轴与重力方向的夹角在竖直平面的投影。当椭球颗粒为完全无规取向时S=0;当椭球颗粒取向完全一致时S=1。S可作为特征轴取向离散性的一个度量,S接近0,离散性越强,取向越无序;S接近1,离散性越弱,取向越有序。

图3为取向角的测量示意。沿特征轴方向的钻孔在二维断面成像中会出现钻孔的投影,借助投影的位置及形状可以有效地确定特征轴的方向,以尽量消除人为判断引入的误差。图4为实验步骤框图。

图3 取向角的测量示意

图4 实验步骤框图

3 实验结果

通过实验获得了椭球模型随机紧密堆积体系的3个参数:堆积分数、取向序和配位数,同时研究形状因子(纵横比)对这3个参数的影响,相关实验数据见表2。

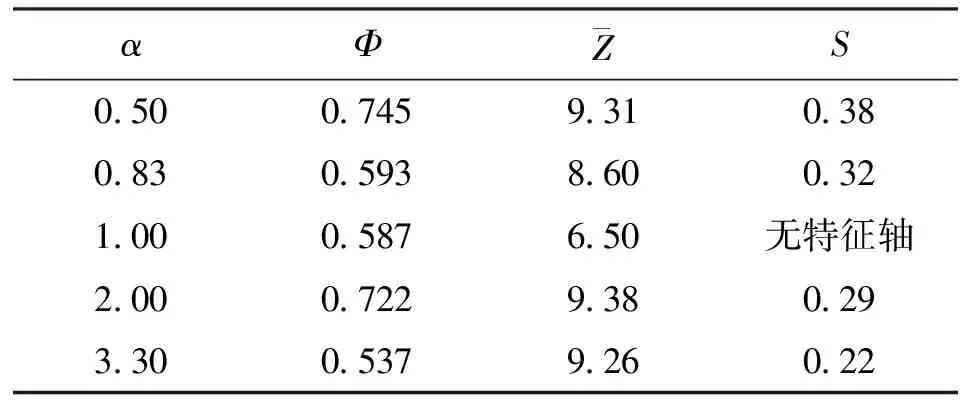
表2 堆积体参数实验结果

3.1 随机紧密堆积分数

图5为5种纵横比下椭球的随机紧密堆积分数的实验结果。图中误差棒代表了不确定度的大小,由误差传递公式计算。图5实验表明:堆积分数在纵横比为0.5和2.0附近出现峰值,当纵横比进一步提高会有下降的趋势;球体的随机紧密堆积分数在0.60左右,而椭球的最高可达0.745。

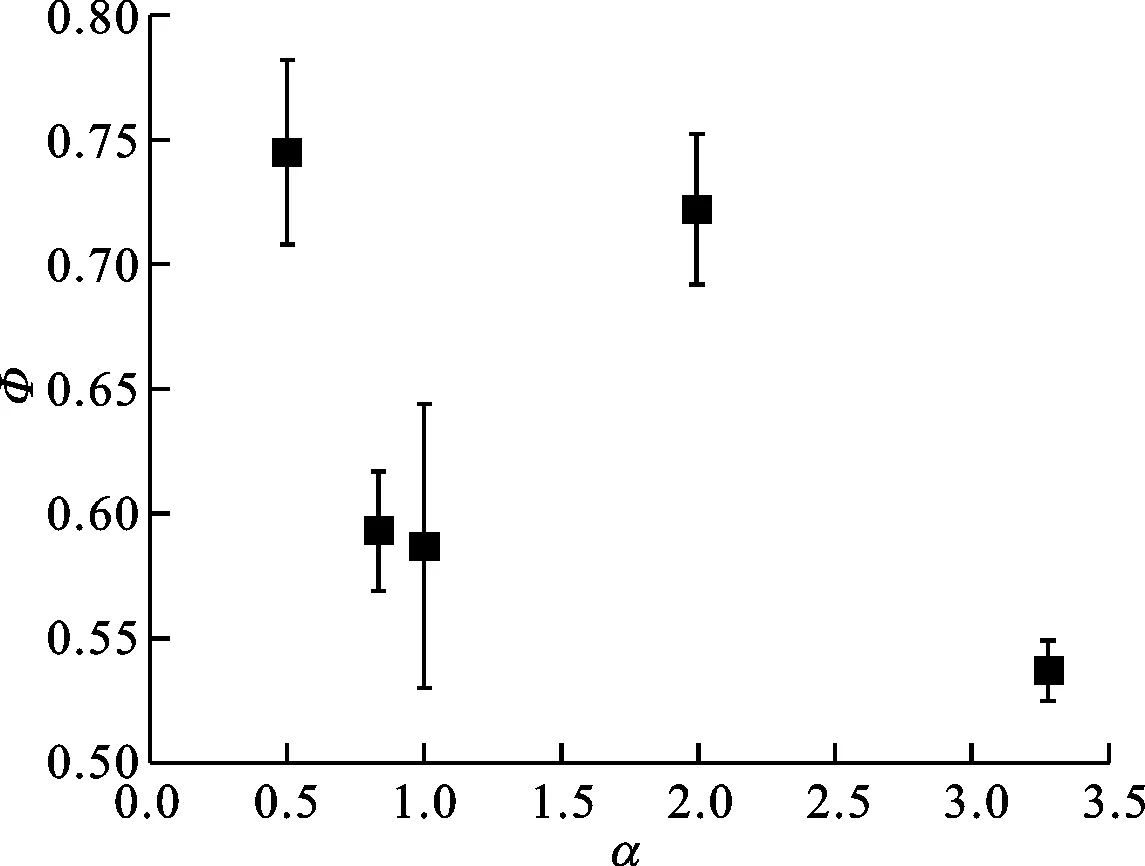
图5 5种纵横比下椭球随机紧密堆积分数的实验结果

3.2 配位数分布

图6为椭球配位数概率分布的实验结果,纵横比为1时是球体。图6实验表明,球体配位数呈正态分布,拟合参数中方差为0.87,均值为6.5,与仿真结果[10]一致。

图6 不同纵横比下配位数概率分布的实验结果

由图6还可以看出:纵横比变化(不为1)时,配位数8、9、10出现的概率(约为85%)最大,纵横比为1时,配位数6、7出现的概率最大;椭球的配位数基本呈偏态分布,而球体配位数呈正态分布。

3.3 取向角分布

图7为不同纵横比下取向角的分布,0°基准轴代表重力方向。图7实验表明:取向角关于参考轴成近似对称分布,但离散性较强;纵横比偏离1越大,取向角在一定区间集中的趋势越明显。

图7 不同纵横比下取向角的分布

4 椭球堆积理论

4.1 基本假定

由平衡理论知,若物体只有一个平动自由度,则平衡需要有方向相反、大小相同的两个力;若物体有两个平动自由度,或一个平动自由度、一个转动自由度,则平衡需要两对力,或一对力加一对力矩。依次类推,假设刚体的自由度为d,在不考虑摩擦的情况下,平衡所需的约束数应为2d,即平均配位数为2d。由于堆积体数有限,且堆积颗粒之间存在关联,从简化的角度看,假设配位数分布满足几何分布,当颗粒为无穷时,堆积收敛为正态分布。

综上所述椭球堆积理论[8]的两个基本假定是:①理想情况(不考虑摩擦)下,约束自由度为d的刚体所需平均配位数为2d;②有限数堆积配位数分布概率满足几何分布。

4.2 椭球堆积理论

图8为椭球堆积理论计算结果。考虑一个未充满椭球的容器,若此时继续增加一个椭球,由假定①易得最概然配位数约为d,由图8b知,该椭球的中心可能落在纵向矩形着色区域,概率为λ,但落在横向矩形着色区域更稳定,假设横向矩形区域的配位数为d-1,则平均配位数满足

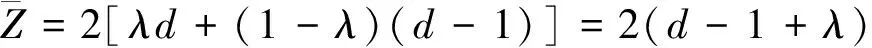
(3)

其中λ满足:纵横比α>1,λ=3/2-(1/2)α;α<1,λ=1/2+(1/2)α2。

由假定②经过推导可得配位数Z的分布概率

(4)

其中p=(d+λ-1)/2d,同时给出随机堆积分数的表达式,并将随机堆积分数看作配位数为Z的球体紧密堆积分数的加权,则有

(5)

值得指出的是,理论值只适用于纵横比为1附近的有限区域,而本文利用该理论解释了实验参数的变化趋势。

4.3 趋势解释

(a)不同纵横比下的配位数分布

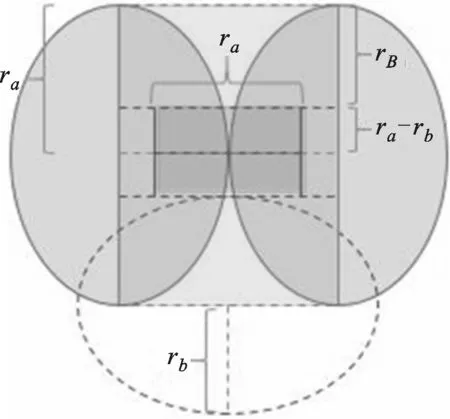
(b)椭球颗粒堆积平衡区域

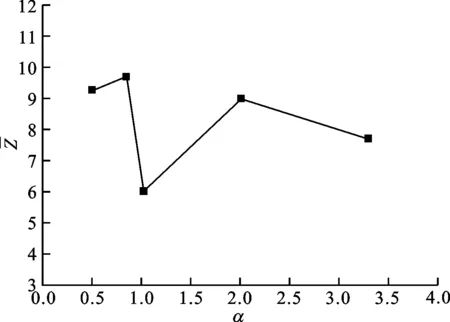
(c)不同纵横比下的平均配位数分布

(d)不同纵横比下的随机紧密堆积分数分布

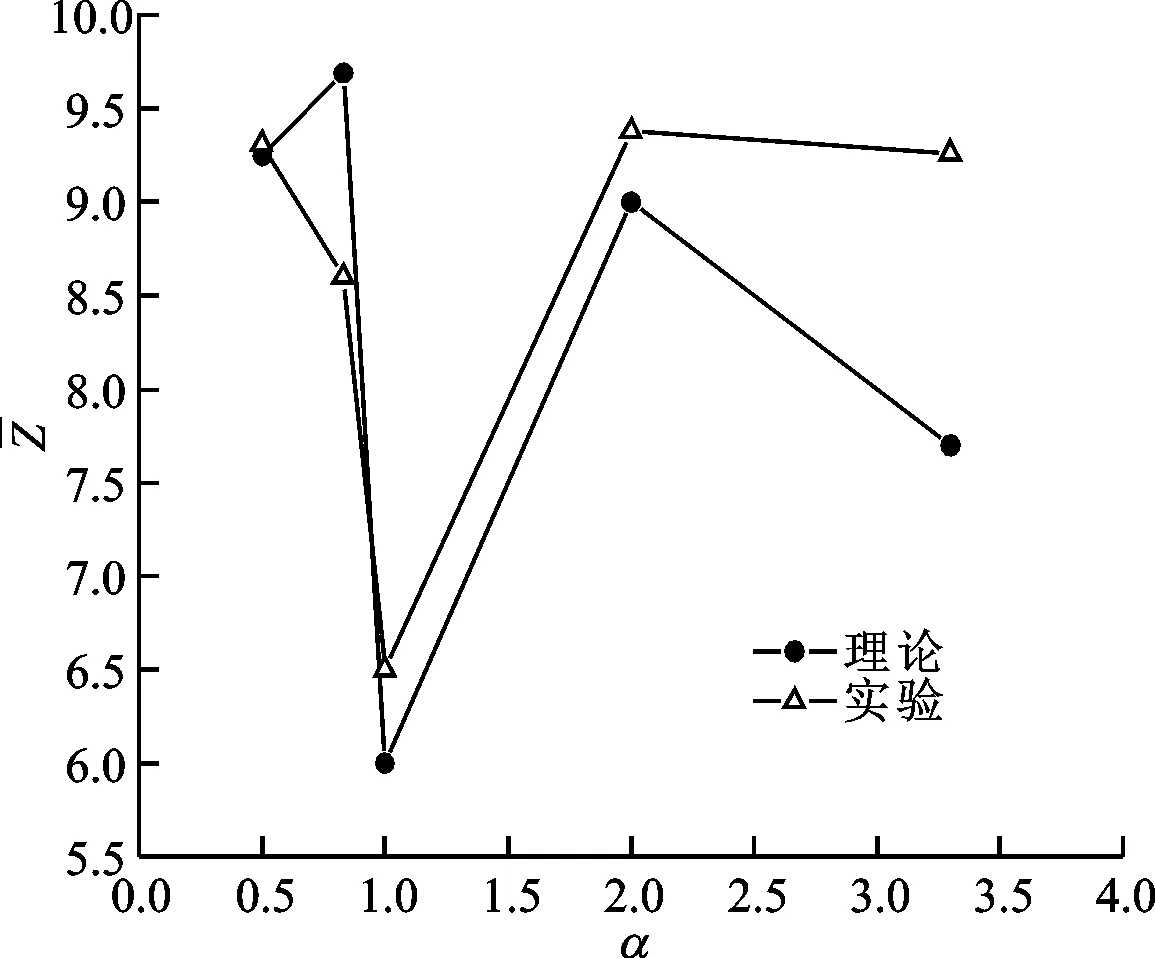
(e)平均配位数实验和理论对比

(f)随机紧密堆积分数实验和理论对比图8 椭球堆积理论计算结果

图8a理论配位数分布与图6的实验配位数分布对比可知,理论配位数分布更为均匀,但是配位数为8、9、10的概率仍最大,且与实验结果一致。考虑到椭球堆积理论在纵横比为1附近会失效,该区域的理论值应由球体堆积理论计算而得。经过修正后,平均配位数和随机紧密堆积分数的实验和理论的对比见图8e和图8f。可以看出,虽然变化趋势上呈现较好的一致性,但误差却高达20%,尤其体现在平均配位数上。其原因是:实际堆积容器的体积和颗粒数有限,所以存在边界效应,即边界上堆积分数显著小于内部堆积分数;实际堆积颗粒之间存在摩擦,由此增加了约束;堆积体系没有完全达到随机紧密堆积状态。

5 结 论

本文实验研究了具有大量随机椭球颗粒模型的紧密堆积系统,选取了5种不同形状因子(纵横比)的堆积样本,包括扁椭球、长椭球、球体。利用工业CT进行了无损堆积成像,得到了取向角和配位数的分布,计算了堆积体系的随机紧密堆积分数、取向序和平均配位数,通过实验测量给出了这些特征量随纵横比的变化。实验结果表明:当椭球纵横比为0.5左右时,随机紧密堆积分数最大值为0.745,远大于球体所能达到的0.6;对于椭球模型,配位数为8、9、10出现的概率最大,而球体模型的最大概然平均配位数为6.5左右;椭球模型取向角关于取向轴呈对称分布,取向角的离散性与形状因子(纵横比)有关。

需要指出的是,椭球模型随机紧密堆积特性与球体模型有较大的差异,以往研究中把椭球转换为当量球体,借助球体研究椭球体的做法缺乏合理性。以上结果对于进一步深入研究各种非球形颗粒堆积物的填充问题具有参考价值。

[1] HALES T C. A proof of the Kepler conjecture [J]. Ann Math, 2005, 162: 1065-1185.

[2] ZALLEN R. The physics of amorphous solids [M]. New York, USA: Wiley, 2008: 49-58.

[3] TAUBERT F, JAHN M W, DOBNER H J, et al. The structure of tropical forests and sphere packings [J]. Proceedings of the National Academy of Sciences, 2015, 112(49): 15125-15129.

[4] YANG J, WANG J, BU S, et al. Experimental analysis of forced convective heat transfer in novel structured packed beds of particles [J]. Chemical Engineering Science, 2012, 71: 126-137.

[5] WEITZ D A. Packing in the spheres [J]. Science, 2004, 303(5660): 968-969.

[6] SONG C, WANG P, MAKSE H A. A phase diagram for jammed matter [J]. Nature, 2008, 453(7195): 629-632.

[7] BERNAL J D, MASON J. Packing of spheres: coordination of randomly packed spheres [J]. Nature, 1960(188): 910-911.

[8] ZHAO J, LI S X. Numerical simulation of random close packing in particle deformation from spheres to cubes [J]. Chin Phys Lett, 2008, 25(11): 4034-4037.

[9] DONEV A, CISSE I, SACHS D, et al. Improving the density of jammed disordered packings using ellipsoids [J]. Science, 2004, 303(5660): 990-993.

[10]DONEV A, STILLINGER F H, CHAIKIN P M, et al. Unusually dense crystal packings of ellipsoids [J]. Physical Review Letters, 2004, 92(25): 255506.

[11]LI S X, ZHAO J. Sphere assembly model and relaxation algorithm for packing of non-spherical particles [J]. Chin J Comp Phys, 2009, 26(3): 167-173.

[12]MAN W, DONEV A, STILLINGER F H, et al. Experiments on random packings of ellipsoids [J]. Physical Review Letters, 2005, 94(19): 198001.

[13]DONEV A, CONNELLY R, STILLINGER F H, et al. Under constrained jammed packings of nonspherical hard particles: ellipses and ellipsoids [J]. Physical Review: E, 2007, 75(5): 051304.

[14]SCHALLER F M, NEUDECKER M, SAADATFAR M, et al. Tomographic analysis of jammed ellipsoid packings [C]∥AIP Conf Proc. Melville, NY, USA: AIP, 2013: 377-380.

[15]SCHALLER F M, NEUDECKER M, SAADATFAR M, et al. Local origin of global contact numbers in frictional ellipsoid packings [J]. Physical Review Letters, 2015, 114(15): 158001.

[16]杨福家, 王炎森, 陆福全. 原子核物理 [M]. 上海: 复旦大学出版社, 1993: 321-327.

[17]董炎明, 朱平平, 徐世爱. 高分子结构与性能 [M]. 上海: 华东理工大学出版社, 2010: 179-180.

[本刊相关文献链接]

吴继琸,朱刚贤,陆斌,等.自愈合效应对光内送粉激光变斑熔覆成形薄壁件的影响.2016,50(1):145-150.[doi:10.7652/xjtuxb201601022]

蔡建程,董博,刘艳华.SiO2颗粒对甲醛及NO的吸附特性研究.2013,47(5):126-130.[doi:10.7652/xjtuxb201305023]

张凯,陈天宁,王小鹏.非阻塞性颗粒阻尼器内部的颗粒莱顿弗罗斯特现象.2016,50(8):15-19.[doi:10.7652/xjtuxb 201608003]

汪映,黄智勇,柯希春,等.液化石油气对二甲醚-柴油双燃料发动机燃烧和排放特性的影响.2016,50(5):19-23.[doi:10.7652/xjtuxb201605003]

瞿磊,王忠,李瑞娜,等.甲醇/生物柴油燃烧颗粒的结构特征研究.2016,50(5):81-86.[doi:10.7652/xjtuxb201605012]

陈斌,胡平舸,屈丹.子空间域相关特征变换与融合的语音识别方法.2016,50(4):60-67.[doi:10.7652/xjtuxb201604010]

方文振,粘权鑫,张虎,等.气凝胶及其纤维复合材料等效导热系数预测.2015,49(7):25-29.[doi:10.7652/xjtuxb2015 07005]

方江龙,王小鹏,陈天宁,等.动理论在预测非阻塞性颗粒阻尼能量耗散中的应用.2015,49(4):12-17.[doi:10.7652/xjtuxb201504003]

姜博,鲁中良,苗恺,等.凝胶注模制备空心涡轮叶片陶瓷铸型的颗粒偏析控制.2014,48(10):77-83.[doi:10.7652/xjtuxb201410012]

谭超,魏正英,魏培,等.内送粉超音速等离子喷涂颗粒飞行状态分析.2014,48(6):91-97.[doi:10.7652/xjtuxb201406 016]

张超,陈天宁,王小鹏,等.颗粒阻尼线性离散元模型参数的选取方法.2014,48(3):96-101.[doi:10.7652/xjtuxb201403 018]

缪金,董明,温福新,等.ZnO纳米颗粒改性变压器油介质损耗模型研究.2014,48(2):50-55.[doi:10.7652/xjtuxb201402 009]

(编辑 苗凌)

Experiments for Randomly Close Packing of Ellipsoids

ZHAO Shumin,HU Zhigang

(School of Science, Xi’an Jiaotong University, Xi’an 710049, China)

Random packing has important significance in both mathematical field and practical application. For a randomly close packing of ellipsoidal particle system, three important parameters, namely stacking fraction, orientational order and coordination number distribution, are accurately measured by an experimental method based on high resolution industrial CT nondestructive testing. The experimental results show that: When the aspect ratio of ellipsoid is 0.5 or 2.0, packing fraction reaches the maximum; The maximum packing fraction is 0.745 ±0.037; Within the scope of the aspect ratio of the test sample, the distribution of coordination number obeys skewed distribution; The orientation angle has high symmetry on the orientation axis. These results are quite different from those of the sphere randomly close packing. An ellipsoid packing theory is proposed under two assumptions to explain the variation trend of the packing parameters. The theoretical simulation results coincide with the experimental ones. The conclusion and the experimental means are of some reference value for researching theory of non-sphere filling and calculation of bulk porosity.

random close packing; packing fraction; coordination number; orientational order

2016-03-07。 作者简介:赵述敏(1977—),女,讲师。 基金项目:国家自然科学基金资助项目(11374237);中央高校基本科研业务费专项资金资助项目(xjj2016060)。

时间:2016-06-14

10.7652/xjtuxb201609022

O4

A

0253-987X(2016)09-0140-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160614.1723.016.html