以轮廓曲线为特征的断裂面匹配

李群辉,张俊祖,耿国华,周明全

(1.长安大学理学院,710064,西安;2.西北大学信息科学与技术学院,710069,西安;3.北京师范大学信息科学与技术学院,100875,北京)



以轮廓曲线为特征的断裂面匹配

李群辉1,张俊祖1,耿国华2,周明全3

(1.长安大学理学院,710064,西安;2.西北大学信息科学与技术学院,710069,西安;3.北京师范大学信息科学与技术学院,100875,北京)

现有断裂面匹配算法主要适用于表面粗糙特征丰富的断裂面,对于表面光滑特征稀少的断裂面不能正确匹配。针对这一问题,提出一种以断裂面轮廓曲线为特征的匹配算法。该算法首先将区域生长算法和边界跟踪算法相结合,在沿碎块棱边分割出断裂面的同时又得到了封闭且序列化的轮廓顶点;轮廓曲线的匹配,先采用角点距离矩阵进行粗匹配,排除了大部分不匹配的曲线对,再根据轮廓曲线所有顶点的曲率和挠率,采用改进的Hausdorff距离进行细匹配;最后,根据匹配的轮廓曲线,采用四元数法计算三维变换将碎块对齐,通过跨界切矢连续检测且误差最小的碎块对为最优匹配。在断裂面粗糙和光滑且材质不同的多个碎块上进行了实验,结果表明该算法能较好实现特征稀少或丰富的断裂面的匹配。

断裂面匹配;断裂面分割;轮廓曲线匹配;跨界切矢连续检测

刚性物体破碎后形成若干任意形状的子物体,利用计算机实现破碎刚体的虚拟复原在文物保护、工业设计和医学等领域有着重要的应用价值,其中断裂面匹配是刚体复原中的关键技术。

现有的断裂面匹配算法主要是基于特征点或特征区域的,Papaioannou等采用Z-buffer算法获得断裂面的深度图像进行匹配[1]。Chen等提出基于曲率形状描述子的特征点匹配算法[2]。Huang等提出基于积分不变量和特征区域的匹配算法[3]。Winkelbach等直接根据断裂面的所有顶点,采用随机采样算法和分级二叉树进行碎块的配对[4]。王坚等以自旋图为特征进行断裂面匹配[5]。Altantsetseg等采用基于傅立叶变换的方法提取断裂面上的曲线作为特征进行匹配[6]。Pokrass等对断裂面进行离散采样得到若干采样点进行匹配[7]。

这类算法均要求断裂面粗糙具有丰富的特征,当断裂面光滑特征稀少时,因缺少足够的特征而无法进行正确匹配,如图1、2所示。与基于特征的算法不同,Papaodysseus首先将两个待匹配碎块根据中心轴旋转对齐,然后依次根据两个拼接断裂面间的间隙体积、重合面积、重合部分的曲率相似度及其边界重合程度判断两碎块是否匹配[8],该算法要求断裂面整体接近平面。

图1 断裂面粗糙的碎块

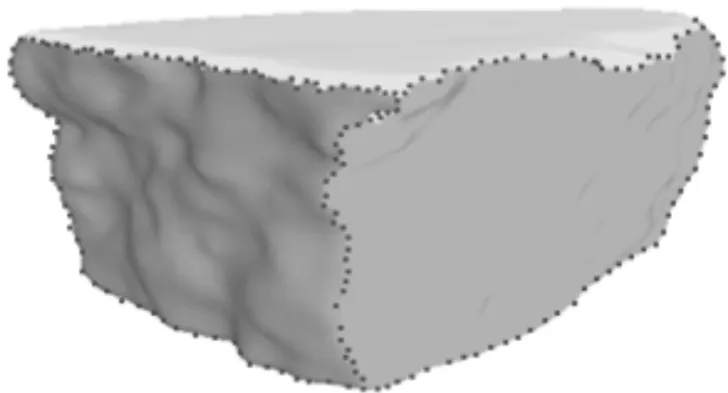
针对这一问题,本文提出以轮廓曲线为特征的断裂面匹配算法,因为无论断裂面的特征丰富与否,如果两个断裂面匹配,除了其中一个断裂面是另一个的子曲面,即当其中一个碎块表面全为断裂面的情形时,这两个断裂面的轮廓有可能没有重合部分,其余情况下两断裂面的轮廓曲线都会部分或全部匹配,如图2所示。

图2 断裂面光滑的碎块

1 轮廓曲线的提取

为了提取出断裂面的轮廓曲线,首先将碎块的外表面沿棱边分割成多张曲面,然后区分出原始面和断裂面,区分的主要依据是断裂面比原始面粗糙,但对于光滑的断裂面则不易区分,本文在曲面分割后,对于光滑的断裂面人工标记,对于粗糙的断裂面算法自动识别。

曲面分割主要有基于面的方法和基于边的方法[9],不足之处是在边界处容易形成锯齿状,边界划分不够准确,且容易产生错误跟踪,不一定能得到封闭的轮廓曲线。针对这一问题,本文给出一种将两种方法相结合的算法,首先采用基于面的方法,即区域生长算法进行曲面分割,得到初始边界点;然后对其进行扩展,再采用基于边的方法,即边界跟踪算法提取边界,这样沿棱边分割出了曲面,且得到了封闭的轮廓曲线。

1.1 提取棱边顶点

为了沿棱边进行曲面分割,首先区分出棱边和非棱边顶点,一般情况下棱边较非棱边凹凸程度显著,曲率能很好地描述局部曲面的凹凸程度,但离散曲率的计算对噪声敏感,所以采用多尺度的曲率信息基于边的方法不足之处是因为在小尺度上局部噪声对曲率影响较大,当增大尺度时对曲率影响就会逐渐减小。根据最大最小主曲率定义的曲度能较好地区分出棱边和非棱边顶点,如图3所示。

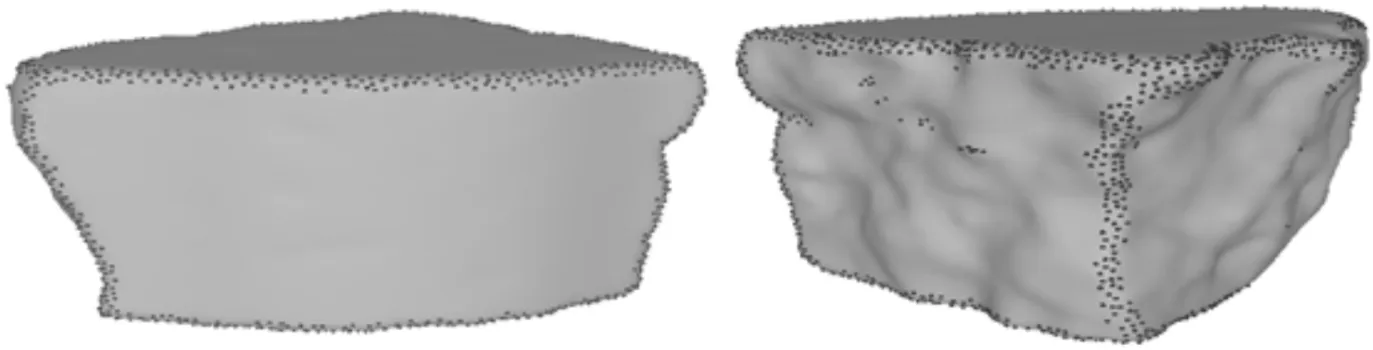
图3 根据曲度提取的棱边点

定义顶点v在尺度rk下的曲度

(1)

式中:rk为顶点v的k阶邻域的顶点个数,k=1,3,5;k1、k2为rk下的最大、最小主曲率,根据k阶邻域顶点进行曲面拟合求出[9]。对于每一个顶点v,如果在rk下的Cv(rk)均大于给定阈值T(rk),则顶点v为棱边顶点。

对于粗糙的断裂面,算法会将少量非边界顶点提取出来,这些顶点曲面分割时会被当成边界点,从而形成一些小面片,最后通过曲面融合算法将其合并到相邻曲面中。

1.2 提取轮廓曲线

本文采用文献[1]中的区域生长算法进行曲面分割,以顶点曲度进行生长。以法矢进行曲面分割,方法简单速度快,对于有尖锐棱边的碎块能进行正确地分割,但当边界过渡较缓慢时,边界分割不准确且容易产生过分割的现象。因为曲度能很好地反映局部曲面的弯曲程度,碎块边界处过渡缓慢或尖锐时通常都有较高的曲度值。边界处和曲面中间有一些独立的小面片,采用曲面融合的方法[1]将其直接合并到相邻较大曲面中,结果如图4所示。

在每一个曲面的生长过程中,遇到的棱边顶点为该曲面的边界点,但边界处有锯齿现象,且边界点没有序列化,为此对边界点进行了扩展,将每个边界点一阶邻域内所有顶点作为候选边界点,更准确的边界点应该是其子集,然后采用边界跟踪算法[9]从候选边界点中重新提取了边界点,同时进行序列化,扩充后的边界点不存在间断的地方,故可得封闭的轮廓曲线,边界顶点如图4c所示。

(a)曲面分割 (b)曲面融合

(c)边界顶点图4 曲面分割及轮廓曲线提取结果

2 轮廓曲线匹配

因为一对碎块的任意两个断裂面都要参加匹配检测,但实际上最多只有一对为真匹配,为了提高匹配的速度和准确率,采用两级匹配算法,即先用快速粗匹配排除大部分不匹配的曲线对,然后再细匹配。归一化的角点距离矩阵能实现曲线的部分匹配,计算简单速度快,具有平移旋转和缩放不变性,能去除大部分不匹配的曲线对,减少下一步参加细匹配的曲线数量。

2.1 根据角点距离矩阵进行粗匹配

文献[10]利用角点距离矩阵对二维轮廓曲线进行粗匹配,本文将其扩展用于空间曲线的匹配。采用角点检测器[11]提取出轮廓曲线的角点,定义曲率的乘积

(2)

式中:k(σj)为尺度σj下的曲率。将|P|大于给定阈值的局部极大值点作为角点。

对于有n个角点的轮廓曲线,距离矩阵是一个n阶方阵,第i行是第i个角点与其余角点间的欧氏距离。设轮廓曲线有p1,p2,…,pn共n个角点,坐标分别是(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn),角点距离矩阵为

(3)

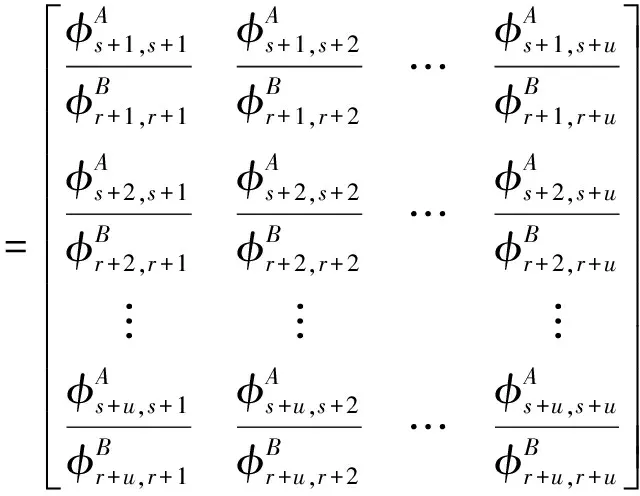
(4)

理想情况下矩阵φ的各项值都为1,但实际会有一定的误差,定义两曲线的相似程度ω=(Σ(1-φi,j)2)1/2,ω越小,两曲线相似度越高。

根据角点距离矩阵进行粗匹配,只利用了轮廓曲线的角点信息,没有考虑角点间曲线段的信息,因此可能会存在一些误匹配,如图5所示,根据角点信息认为曲线段abcd和a′b′c′d′是匹配的,但实际上角点bc和b′c′之间的曲线段并不匹配,因此还需要对角点间的曲线段进一步细匹配。

(a)待匹配曲线 (b)匹配结果图5 根据角点距离矩阵的粗匹配结果

2.2 根据Hausdorff距离和曲率挠率细匹配

空间曲线的曲率和挠率能唯一确定一条曲线的形状,采用顶点的曲率、挠率组成的特征串描述两角点间的曲线段。Hausdorff距离可从总体上衡量两个点集之间的距离,不需要点的对应关系,当点集数量不大时,采用基于平均值并加入曲线段长度信息的Hausdorff距离衡量两曲线段的相似度。

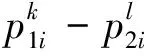
(5)

C1i和C2i间引入方差信息和曲线段长度信息的Hausdorff距离[13],即

‖p1i-p2i‖+

kS(C1i,C2i)+tΔN

(6)

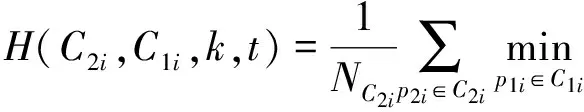
kS(C2i,C1i)+tΔN

(7)

式中:NC1i、NC2i分别为C1i、C2i顶点的个数;k为权重系数,表示顶点分布在相似性比较中所占的比重;ΔN=|C1i-C2i|为C1i和C2i顶点个数的差,用来衡量C1i和C2i的长度差;t为加权系数,表示曲线段长度差异在Hausdorff距离中所占的权重。

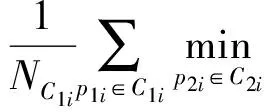
(8)

(9)

与传统Hausdorff距离相比,改进的Hausdorff距离使用曲线段点集间的平均最小距离,并引入方差信息和曲线段长度信息,对噪声和离群点的鲁棒性更好,对曲线段的描述更精确。

一般情况下,H(C1i,C2i,k,t)和H(C2i,C1i,k,t)不相等,为了进一步减少离群点的影响,令

(10)

如果H(C1i,C2i,k,t)<ε2,说明曲线段C1i和C2i匹配,ε2为经验阈值。粗匹配得到的轮廓曲线C1和C2每一对对应曲线段C1i和C2i,如果均匹配,则轮廓曲线C1和C2匹配。

3 断裂面匹配

两轮廓曲线匹配后,还需要再根据跨界切矢是否连续进一步检测其所在的断裂面是否为真匹配。设C1、C2为断裂面F1、F2的轮廓曲线,利用四元数法[14],计算C1、C2间的旋转矩阵R和平移矩阵T,将断裂面F1、F2对齐,如果F1、F2为真匹配,则C1、C2在对应点处应满足G1连续(切矢同向),如图6所示。跨界切矢连续检测要求两顶点序列一一对应,但由于断裂面边界的复杂性,匹配的轮廓曲线顶点序列并不是等间距的,重新采样会带来新的误差和系统开销,而匹配的轮廓曲线角点序列是对应的,因此根据对应角点来进行跨界切矢连续检测。

图6 跨界切矢连续图示

4 实验结果和分析

文中实验数据包括6块石头碎块brick和11块灰泥碎块cake,是Vienna University of Technology公开用于复原的部分碎块模型[15],原始碎块是点云模型,对其进行三角剖分并优化可得三角网格模型。马腿碎块是在兵马俑采集的,用Handy3dscan三维激光扫描仪直接得到三角网格数据。因为断裂面的匹配是互补匹配,所以先将其中一个断裂面的法矢反向。文中所有算法用Visual C++和OpenGL编程,在CPU为Pentium(R)/3.4 GHz、内存为8.0 GB的PC机上实现。

对于cake和brick碎块,由于断裂面比较粗糙,算法可根据其粗糙程度自动区分出断裂面和原始面。实验过程是手动选择两个碎块,然后系统自动分割出其断裂面和原始面,之后会在所有断裂面间自动进行匹配。对于马腿碎块,因无法区分出断裂面和原始面,采取人工交互的方式选择两个断裂面进行匹配。

断裂面光滑的3个马腿碎块断裂面分割、轮廓曲线和角点提取及匹配结果如图7所示,其中F2、F3是碎块2的两个不同的断裂面,断裂面F1、F2的轮廓曲线完全匹配,F3、F4的轮廓曲线也完全匹配,通过跨界切矢连续检测,相应断裂面也完全匹配。断裂面粗糙的2个brick碎块曲面分割、轮廓曲线和角点提取及匹配结果如图8所示,其中断裂面F2和F1只有部分轮廓曲线匹配。brick碎块和cake碎块的匹配结果如图9所示,其中cake碎块的第i块和第j块匹配记为cakei-j,brick碎块的第i块和第j块匹配记为bricki-j。由图9可知,本文算法对于光滑或粗糙断裂面均适合,且能实现断裂面部分和完全匹配。

图7 马腿碎块和匹配结果

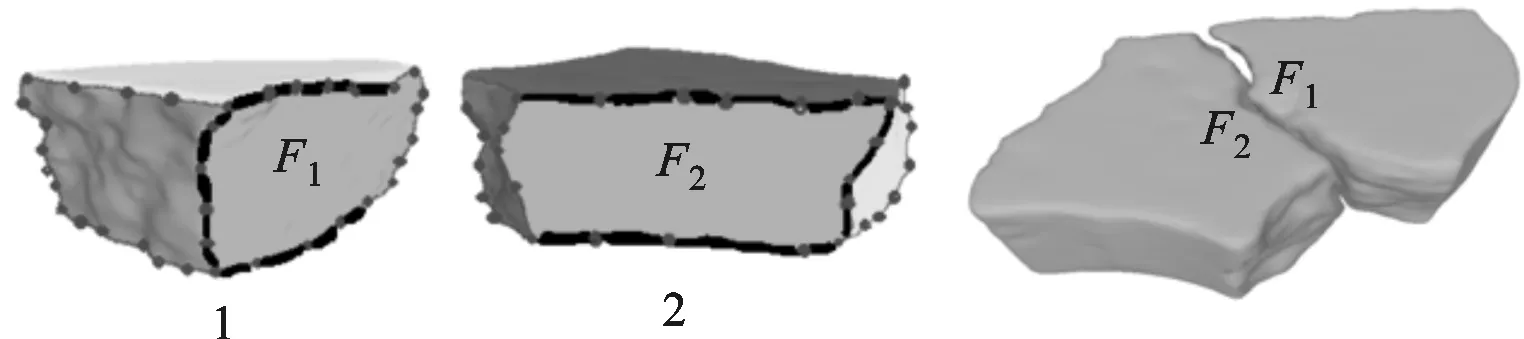
图8 birck碎块和匹配结果

(1)cake1-3 (2)cake2-4 (3)cake7-8

(4)cake6-7 (5)cake9-10 (6)cake2-10

(7)brick1-2 (8)brick1-3 (9)brick2-5 (10)brick5-6图9 匹配结果

图9中各个碎块的大小、包含的断裂面数目、需匹配的断裂面对数目和算法执行时间如表1所示,其中碎块的大小指其包含的三角网格数目,执行时间是指碎块所有断裂面间的匹配时间,包括本文算法中所有步骤,分别是曲度的计算、轮廓曲线的提取及相似性计算、平移旋转变换的计算和跨界切矢连续检测。实验中10对碎块,共有59对断裂面进行了匹配,平均每对断裂面匹配时间为2.78 s。

表1 碎块大小、断裂面数目和算法执行时间

图10 无法识别的匹配碎块

算法的准确程度受各个阈值影响较大,但如何选取合适的阈值是算法的难点,各阈值取值和碎块的网格精度、尺寸、材质等因素有关,通过统计获取初始阈值,然后根据实验结果人工进行调整获得最终阈值。对于轮廓比较复杂或轮廓曲线重合较少的碎块,算法可能存在着不能正确匹配的情况,如图10所示。由图10可知,这两个断裂面标出的部分应该是匹配的,即一个断裂面和另一个断裂面部分匹配。还有一种情况是因为算法采取角点距离矩阵进行轮廓曲线的粗匹配,所以当轮廓曲线无角点或只有一个角点时,本文算法无法使用。

5 结 论

针对当前断裂面匹配算法大多只适合表面粗糙特征丰富的断裂面、表面光滑特征稀少的断裂面无法匹配的现状,本文提出以轮廓曲线为特征进行断裂面匹配。算法通过将区域生长算法和边界跟踪算法相结合,避免了两个算法各自的不足之处,分割出的断裂面边界光滑准确,提取的轮廓顶点形成封闭且序列化的曲线。采用的两级轮廓曲线匹配算法,先排除了大部分不匹配的轮廓曲线,大大减少了细匹配的搜索空间,提高了匹配的速度和准确率。以轮廓曲线为特征,不要求断裂面必须具有丰富的特征,因此对于光滑和粗糙的断裂面均适合,实验结果表明该算法能实现较复杂碎块的匹配,且具有较快的匹配速度。

[1] PAPAIOANNOU G, EVAGGELIA A K. Reconstruction of three-dimensional objects through matching of their parts [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(1): 184-187.

[2] CHEN Hui, BHANU B. 3D free-form object recognition in range images using local surface patches [J]. Pattern Recognition Letters, 2007, 28(10): 1252-1262.

[3] HUANG Q X, FLORY S, GELFAND N. Reassembling fractured objects by geometric matching [J]. ACM Transactions on Graphics, 2006, 25(3): 569-578.

[4] WINKELBACH S, FRIEDRICH M. Pairwise matching of 3D fragments using cluster trees [J]. International Journal of Computer Vision, 2008, 78(1): 1-13.

[5] 王坚, 周来水. 基于最大权团的曲面粗匹配算法 [J]. 计算机辅助设计与图形学学报, 2008, 20(2): 167-173. WANG Jian, ZHOU Laishui. Surface rough matching algorithm based on maximum weight clique [J]. Journal of Computer-Aided Design & Computer Graphics, 2008, 20(2): 167-173.

[6] ALTANTSETSEG E, MATSUYAMA K, KONNO K. Pairwise matching of 3D fragments using fast Fourier transform [J]. The Visual Computer, 2014, 30(6): 929-938.

[7] POKRASS J, BRONSTEIN A M. Partial shape matching without point-wise correspondence [J]. Numerical Mathematics: Theory, Methods and Applications, 2013, 6(1): 223-244.

[8] PAPAODYSSEUS C, ARABADJIS D, EXARHOS M. Efficient solution to the 3D problem of automatic wall paintings reassembly [J]. Computers & Mathematics with Applications, 2012, 64(8): 2712-2734.

[9] 刘胜兰. 逆向工程中自由曲面与规则曲面重建关键技术研究 [D]. 南京: 南京航空航天大学, 2004.

[10]曾接贤, 刘秀朋, 符祥. 角点距离矩阵和同心圆划分的曲线描述与匹配 [J]. 中国图象图形学报, 2012, 17(8): 1011-1020. ZENG Jiexian, LIU Xiupeng, FU Xiang. Representation and matching for planar curve based on corner distance matrix and concentric circles [J]. Journal of Image and Graphics, 2012, 17(8): 1011-1020.

[11]张小洪, 雷明, 杨丹. 基于多尺度曲率乘积的鲁棒图像角点检测 [J]. 中国图象图形学报, 2007, 12(7): 1270-1275. ZHANG Xiaohong, LEI Ming, YANG Dan. Robust image corner detection based on multi-scale curvature product [J]. Journal of Image and Graphics, 2007, 12(7): 1270-1275.

[12]丁爱玲, 周琳, 李鹏. 计算机图形学 [M]. 西安: 西安电子科技大学出版社, 2005: 99-104.

[13]刘嘉敏, 王玲, 兰逸君, 等. 基于外耳轮廓边缘信息的人耳识别 [J]. 计算机辅助设计与图形学学报, 2008, 20(3): 337-342. LIU Jiamin, WANG Ling, LAN Yijun, et al. Ear recognition based on the edge information of the auricle contour [J]. Journal of Computer-Aided Design & Computer Graphics, 2008, 20(3): 337-342.

[14]江刚武. 空间目标相对位置和姿态的抗差四元数估计 [D]. 郑州: 解放军信息工程大学, 2009.

[15]HUANG Q X. 3D puzzles: reassembling fractured objects by geometric matching[EB/OL]. [2015-09-29]. http: ∥www.geometrie.tuwien.ac.at/ig/3dpuzzles. html.

(编辑 赵炜)

Fracture Surfaces Matching Based on Contour Curve

LI Qunhui1,ZHANG Junzu1,GENG Guohua2,ZHOU Mingquan3

(1. School of Sciences, Chang’an University, Xi’an 710064, China; 2. School of Information and Technology, Northwest University, Xi’an 710069, China; 3. College of Information Science and Technology, Beijing Normal University, Beijing 100875, China)

The existing matching algorithm of fracture surfaces is mainly suitable for rough surfaces with rich features but not for smooth surfaces with rare features. To solve this problem, an algorithm based on contour curve is proposed for fracture surfaces matching. Firstly, the algorithm combines region growing algorithm and boundary tracking algorithm for surface segmentation and contour extraction simultaneously. Next, the contour matching includes rough matching based on the corner point distance matrix, which can eliminate most of the dissimilar contour pairs, and fine matching based on Hausdorff distance according to the curvatures and torsions of all contour curve vertices. Finally, the quaternion method is used to calculate rigid transformation based on contour pairs. The optimal matching is the fragment pairs which satisfy the cross-boundary continuity detection and have minimum errors. We use a variety of rough and smooth fracture surfaces of different materials to test the algorithm. Experimental results show that the algorithm can achieve better matching of fracture surfaces with rare or abundant features.

fracture surfaces matching; fracture surfaces segmentation; contour curve matching; cross-boundary continuity detection

2015-12-08。 作者简介:李群辉(1975—),女,博士,讲师。 基金项目:国家自然科学基金资助项目(61373117);陕西省科技计划资助项目(2016JM6081)。

时间:2016-07-14

10.7652/xjtuxb201609017

TP301.6

A

0253-987X(2016)09-0105-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1117.006.html