考虑旋转和曲率的湍流模型修正及应用

任芸,吴登昊,牟介刚,李晓俊

(1.浙江工业大学之江学院,310024,杭州;2.浙江理工大学机械与自动控制学院,310018,杭州;



考虑旋转和曲率的湍流模型修正及应用

任芸1,2,吴登昊1,3,牟介刚3,李晓俊2

(1.浙江工业大学之江学院,310024,杭州;2.浙江理工大学机械与自动控制学院,310018,杭州;

3.浙江工业大学机械工程学院,310014,杭州)

通过分析湍流模型在模拟旋转和弯曲壁面的旋转机械内流时存在的问题发现,在原有湍流模型的基础上考虑旋转和曲率效应是提高离心泵内流模拟精度和改善流动不稳定性的必然选择;在k-ωSST模型中通过考虑旋转和曲率修正,同时引入Hellsten的理查德森数修正模型思想和扩展内秉旋转张量修正,生成了一种新的湍流模型;应用改进后的湍流模型对比转数为34.34的离心泵在不同工况下的内流场进行了数值模拟,并将改进前后的数值计算结果与试验结果进行了详细对比,由此分析了泵内部流场的分布规律。研究结果表明:改进后的湍流模型预测的能量性能与试验值更接近;在0.6倍设计流量工况下,改进后湍流模型的扬程预测精度提高了3%,效率预测精度提高了近2%,这一结论在内流场中得到了验证;与原湍流模型相比,改进后湍流模型明显改善了叶轮流道和蜗壳扩散段处的流动情况。该结果可为湍流模型研究提供参考。

湍流模型;离心泵;理查德森数;旋转和曲率修正

离心泵内湍流充斥着整个流道,使流道内湍流结构十分复杂,同时受哥氏力和离心力的影响,旋转和曲率对叶轮内边界层起着增大或抑制的作用[1]。对于低比转数离心泵,叶轮叶片曲率较大,在高速旋转状态下易引起分离流动和旋转流动等不稳定流动,造成蜗壳内的流动损失和叶轮的损害,使泵的扬程和效率下降,因此这种影响不容忽视。数值计算为揭示离心泵内部的复杂流动和指导水力设计提供了一种有效的手段,其中湍流模型对计算的精度有很大影响,尤其是带有旋转和弯曲壁面的旋转机械的内部流动计算[2]。

k-ε模型[3]和k-ω模型[4]是工程上应用最广的涡黏性模型,在强旋流、曲壁边界层等流场中k-ε模型预测精度偏低[5],k-ω模型模拟较复杂,将k-ε模型和k-ω模型相结合的k-ωSST模型[6]体现出一定的计算优势,其对逆压梯度流动(如分离流)的预测效果明显,但对强旋转和大曲率流动模式还存在着偏差。

本文在k-ωSST湍流模型的基础上,考虑旋转和曲率的综合效应,对输运方程的生成项和ω方程的耗散项分别应用Smirnov等发展的旋转曲率修正方法和Hellsten提出的理查德森数(Richardson number,Ri)进行了改进,同时结合非惯性坐标系下旋转张量的修正方法生成了新模型,最后将改进的模型应用于离心泵的内流计算中,为进一步探讨提高预测精度的方法和分析内流机理奠定了基础。

1 旋转和曲率对边界层稳定性的影响

对于弯曲或者旋转流道内的流动,如果按静止平板边界层来计算,必然会带来较大的误差,因为边界层的发展会受到壁面弯曲和系统旋转的影响。Johnston分析了旋转状态下科氏力对边界层稳定性影响的两种效应[7]:第一,如果科氏加速度存在垂直于固体壁面的分量,则科氏力将对湍流结构的稳定性产生影响,即加强或者削弱了湍流稳定性;第二,如果科氏加速度存在平行于固体壁面的分量,则在边界层的平均流场中科氏力将引起垂直于流动方向的二次流。对于凸壁面,曲率具有稳定边界层的作用,对于凹壁面,曲率的作用则相反[8]。在离心叶轮中,受叶轮旋转和叶片曲率的影响,压力面的低能流体沿前后盘表面流向叶片的吸力面,使稳定边的流动经历了从充分湍流到完全层流的过程。吸力面层流化会导致叶片雷诺应力减小,引发边界层分离,而在压力面的情况则相反。

1969年Bradshaw从稳定性分析的角度出发,通过考察二维旋转弯槽中的湍流流动,得到了旋转与平均流线弯曲对剪切层流动影响的重要参数——梯度理查德数(Gradient Richardson Number,Ri),用于描述边界层的稳定性[9]

(1)

式中:wRot为系统旋转角速度;U为流体速度;y为曲率半径的方向;S=-2wRot(∂U/∂y)-1。对于离心叶轮,吸力面上边界层的Ri>0,即该处的流动是稳定的;压力面上边界层的Ri<0,即该处的流动是不稳定的。

随着旋转系统流动情况的日益复杂以及计算流体动力学(CFD)技术的发展,不少学者[10-11]对式(1)进行了重新定义,目前在径流式旋转机械中以Hellsten提出的Ri[12]应用最普遍,他在前人的基础上用时间尺度重新定义了Ri,即

(2)

式中:Ωij=(∂Ui/∂xj-∂Uj/∂xi)/2和Sij=(∂Ui/∂xj+∂Uj/∂xi)/2分别为平均运动的旋转张量和应变变化率张量。

2 旋转和曲率对湍流结构的影响

为了从理论上深入分析旋转和曲率对湍流结构的影响,Johnston从雷诺应力方程与湍流能量分量的生成速率方程出发,分别讨论了旋转和曲率对湍流结构的影响,结论是:湍流生成项虽然不显含旋转和曲率,但是可以通过旋转和曲率来影响雷诺应力及其分量[7-8]。在压力面,雷诺应力和湍流能量生成率增加,湍流能量的水平增加,而在吸力面,湍流能量的水平降低。在凸壁面,曲率受到了抑制,雷诺应力减小,湍流能量水平降低,而在凹壁面则相反。

Menter的k-ωSST湍流模型输运方程的生成项是基于应变率张量的函数,不包含涡张量,在流动分离区应变率张量迅速增加,这对雷诺应力大小和湍流能量水平的预测有很大影响,因此Spalart在Knight和Saffman提出的回转稳态效应(GSE)的基础上,对生成项同时考虑了涡张量和应变率张量,从而建立了一种考虑旋转与曲率影响的修正函数[13]

(3)

(4)

(5)

式中:Csca为经验常数,可以根据具体的流动问题进行调节,一般为1.0。

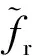
(6)

(7)

S2=2SijSij

(8)

Ω2=2ΩijΩij

(9)

D2=max(S2,0.09ω2)

(10)

(11)

(12)

3 湍流模型的修正

3.1 k-ω SST湍流模型

k-ωSST模型是Menter在BSLk-ω模型的基础上针对边界层流动的特点发展出的一种符合剪切层流动中剪切应力输运的模型。对于不可压流动,k-ωSST模型的输运方程为

(13)

(14)

式中:K是湍动能;PK是湍动能K的生成项,PK=υtS2=2υtSijSij;uj(j=1,2,3)代表与坐标轴xj平行的速度分量;υ是运动黏性系数;υt是涡黏性系数;ω是比耗散率;β*、σK、γ、β、σω、σω2为输运方程中的常数。

混合函数

(15)

(16)

涡黏性系数

(17)

(18)

S=(SijSij)1/2

(19)

3.2 改进的k-ω SST湍流模型

Hellsten根据式(2)定义了旋转和曲率的修正系数

(20)

式中:Crc推荐值为3.6。为了考虑系统的旋转效应,式(2)中用于描述Ri的旋转张量用扩展内秉旋转张量(式(12))替代。

Smirnov等根据Spalart提出的旋转修正函数,对湍流模型中的湍动能生成项PK进行修正[14],即

PK→PKfr

(21)

因此,结合式(20)和式(21),修正后的k-ωSST湍流模型表达式为

(22)

ω2+

(23)

4 数值计算和分析

4.1 计算对象

以低比转数(ns=3.65nQ1/2/H3/4)离心泵作为研究对象,设计参数为流量Q=23 m3/h,扬程H=72 m,转速n=2 900 r/min,比转数ns=34.34,效率η=58;几何参数为叶片数z=4,叶轮进口直径D1=45 mm,叶轮出口直径D2=248 mm,叶轮出口宽度b2=5 mm,蜗壳基圆直径D3=252 mm。为了保证进、出口流动的均匀性,在叶轮进口和蜗壳出口处分别延伸了30 mm和130 mm,其几何模型和网格划分见图1。

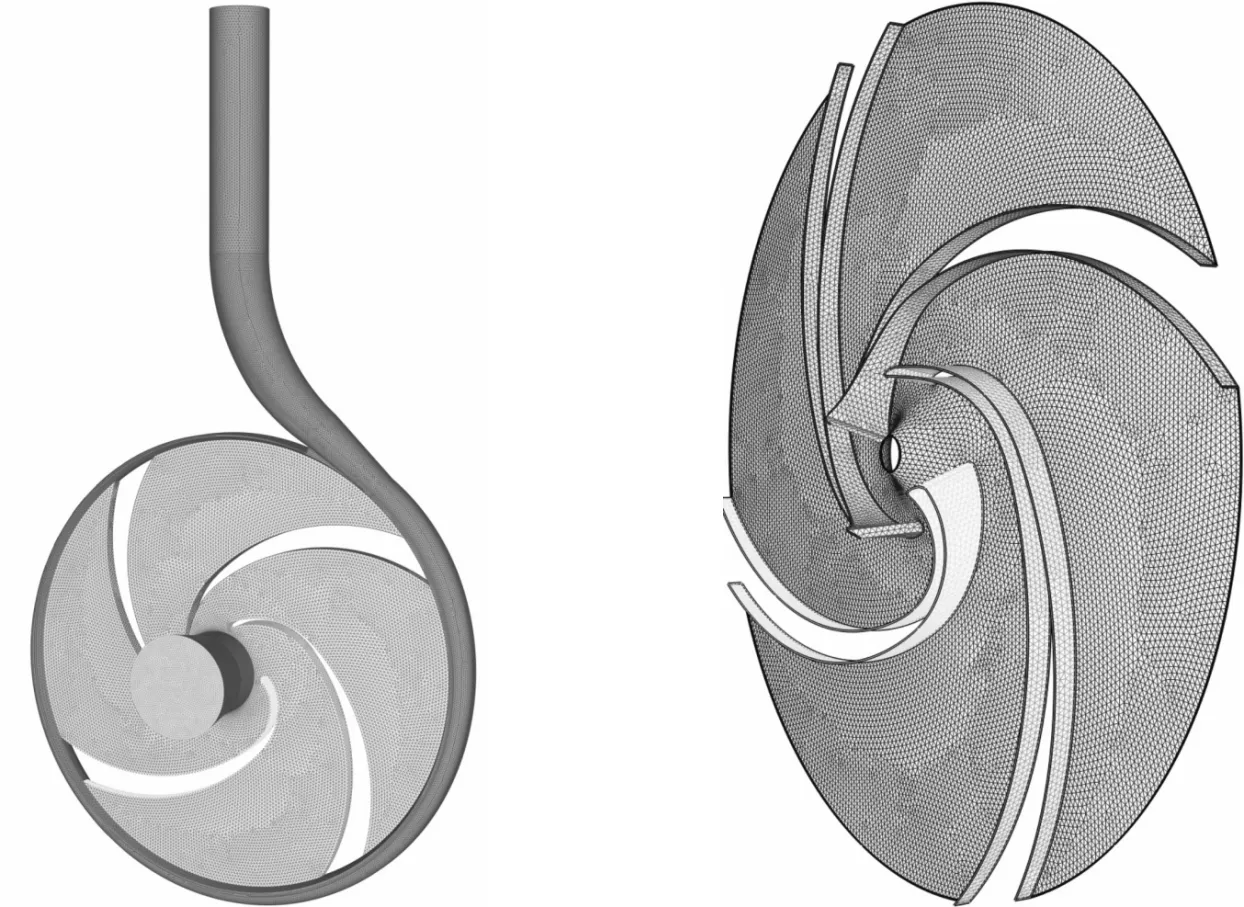
(a)离心泵计算网格 (b)叶轮网格 图1 计算模型及网格划分示意图

4.2 计算方法

在开源软件OpenFOAM的基础上对k-ωSST湍流模型进行了改进,新模型命名为k-ωSST RC。在OpenFOAM中导入模型并指定边界条件如下。

进口条件:速度进口。

出口条件:出口静压P=0 Pa,其他量梯度为0。

壁面条件:所有壁面满足无滑移条件。

动、静部件之间的信息传递采用GGI方法处理,以达到整机计算的目的。

4.3 计算结果与分析

本文采用k-ωSST和k-ωSST RC湍流模型对上述离心泵进行了定常计算。为了避免由网格数引起的数值计算结果误差,设计了6套网格方案进行网格无关性分析,见表1。根据离心泵性能计算式[15-17]、结合试验结果比较了性能以及内部流场的影响。

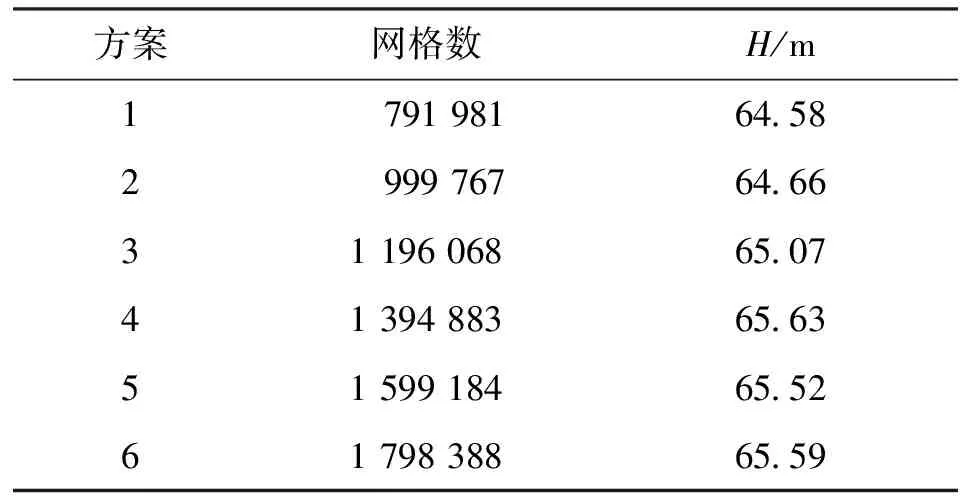
表1 网格无关性分析方案

从表1可以看出,网格数大于139万时,离心泵扬程随网格数的增加波动不再明显,因此本文选择方案4中的网格进行后续研究。

4.3.1 外特性对比分析 表2给出了离心泵在不同设计流量Qd工况下采用k-ωSST(模型1)和k-ωSST RC(模型2)的计算结果。试验是在江苏大学国家一级精度试验台上进行的,该试验台的精度符合GB3216中规定的I级测试精度的要求。

从表2可以看出,当流量减小到0.8Qd时,2种湍流模型的差异明显起来。从外特性上看,k-ωSST RC湍流模型的计算精度虽然与试验值还有一定的偏差,但与k-ωSST模型相比显著提高,尤其是在0.6Qd下,扬程精度提高了3%,效率精度提高了近2%。从迭代步数上看,k-ωSST RC湍流模型计算所需迭代步数明显较少,这说明k-ωSST RC湍流模型在小流量工况下具有较好的特性,值得进一步深入研究。

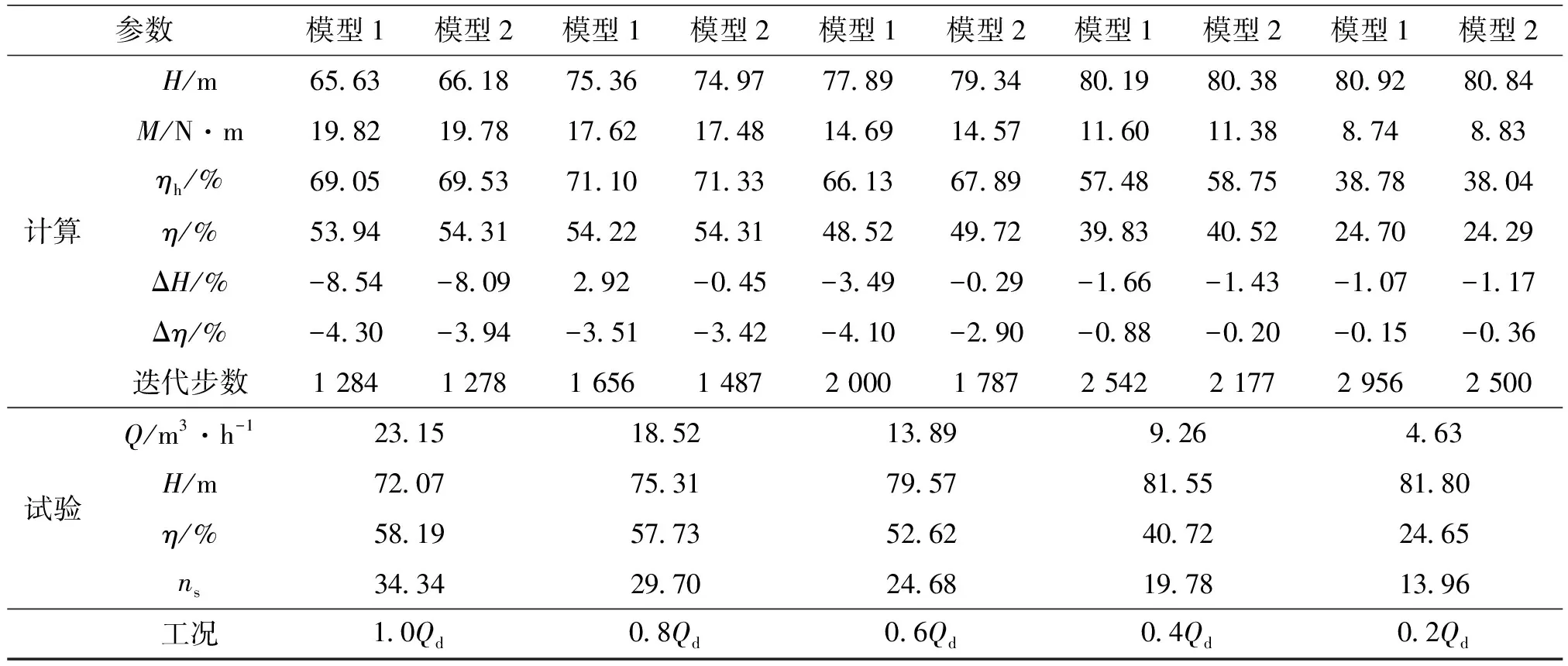
表2 离心泵在2种湍流模型、不同工况下的计算结果

4.3.2 内流场结果分析 为了更全面地比较不同湍流模型的特性和差异,针对0.6Qd工况分别从以下3个方面进行对比分析。

(1)叶轮出口相对速度分布。由图2可以看出,k-ωSST和k-ωSST RC模型获得的叶轮出口的相对速度分布相差无几,区别仅在于靠近隔舌处的叶轮出口处,k-ωSST湍流模型较k-ωSST RC模型的低速区范围稍大。这说明叶轮二次流将低能流体微团馈给前盘-吸力面拐角处的尾流,使尾流面积逐渐增大,而叶轮旋转和流线曲率效应又增强了在射流-尾流剪层处的湍流掺混,这种畸变流动一直保持并在出口处得到增强,所以考虑旋转和曲率效应的湍流模型增强了该叶轮内的射流-尾迹结构。

(a)k-ω SST

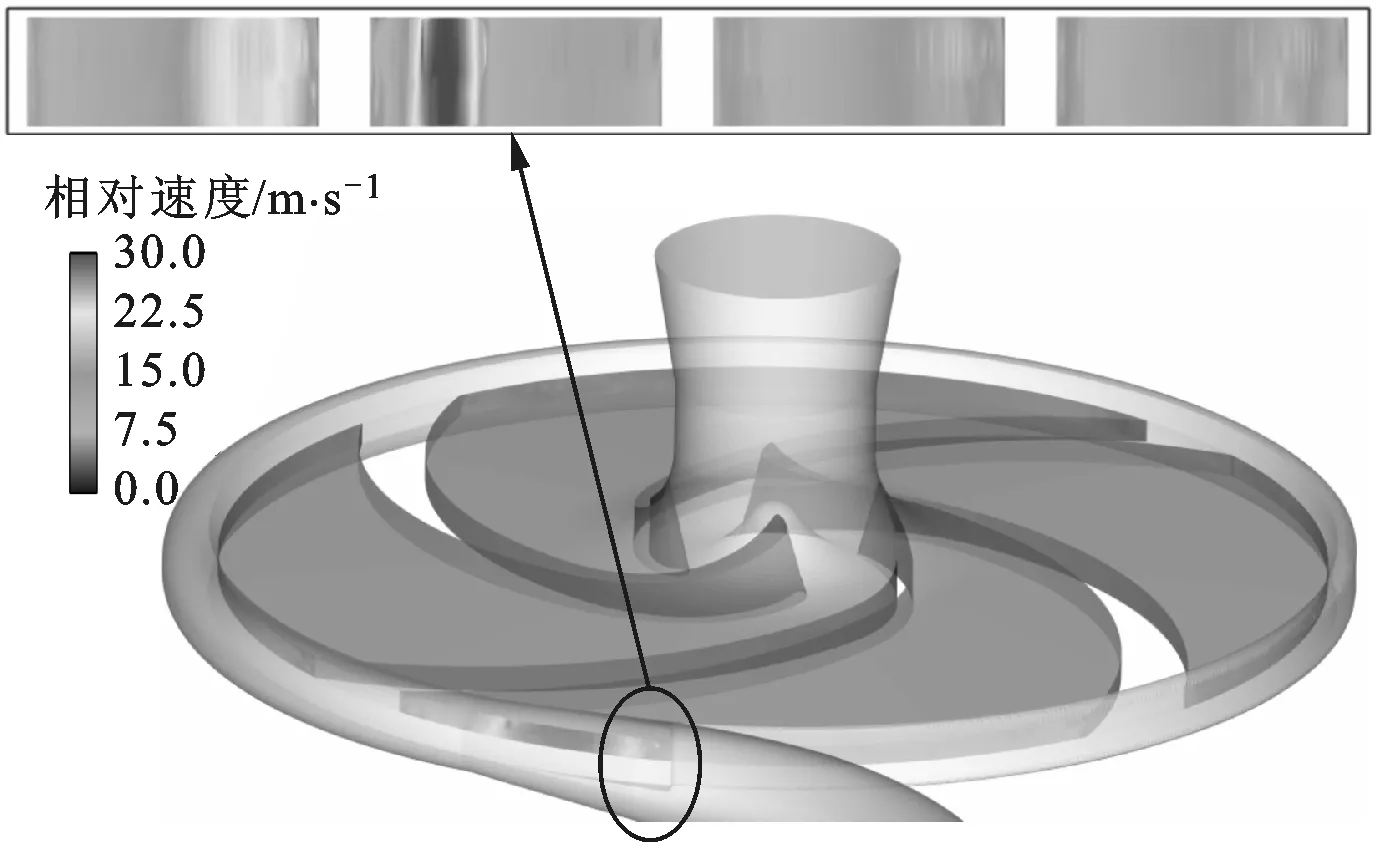
(b)k-ω SST RC图2 叶轮出口处的相对速度分布

(2)湍动能分布。湍动能是衡量湍流掺混能力的重要指标。从图3中可以看到,叶轮吸力面湍流掺混程度和剪应力比较低,而在压力面则相反。随着系统的旋转,雷诺应力将提供一个力使壁面附近做极慢运动的内层流体克服扩压流动中的逆压梯度而向前运动,于是降低了湍流掺混,这将促使叶轮流道中流体产生失速,形成规则的不稳定旋涡。修正后的湍流模型能准确地对叶轮流道内不稳定旋涡进行捕捉。

(a)k-ω SST

(b)k-ω SST RC图3 湍动能分布

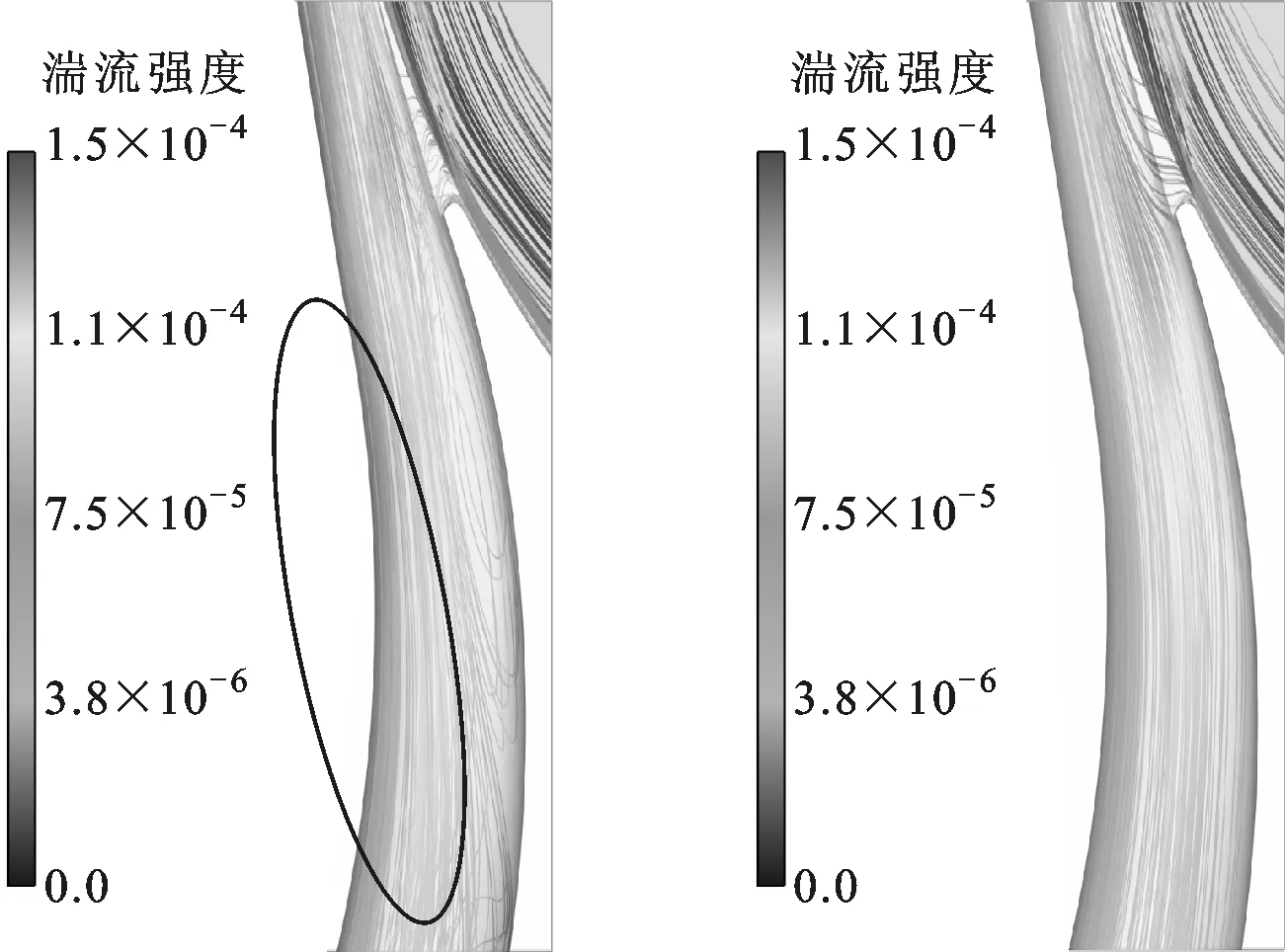
(a)k-ω SST (b)k-ω SST RC图4 湍流强度分布

(3)湍流强度分布。湍流强度是衡量湍流强弱的相对指标。从图4可以看到,没有考虑旋转和曲率效应前,在蜗壳扩散段靠近壁面处存在一定程度的失速,这充分验证了旋转和曲率效应对湍流结构的影响。这样的流动状态会造成流体能量损失,即扬程下降,也是计算时迭代次数增多的原因之一。

5 结 论

本文针对离心泵叶轮流道强旋转、大曲率的特点,分析了常用的二方程湍流模型的不足,在k-ωSST湍流模型的基础上,综合了Spalart和Hellsten的旋转和曲率修正方法,分别对湍动能生成项和ω方程的耗散项进行了修正,同时考虑了扩展内秉旋转张量的修正。通过对比改进前、后的湍流模型的计算结果,得到以下结论。

(1)在外特性方面,改进后的湍流模型的计算结果更接近试验值,尤其是在0.8Qd下扬程精度提高了2%,在0.6Qd下扬程精度提高了3%,效率精度提高了近2%。

(2)在小流量工况下,随着进口冲角的增加,叶轮内更易出现失速,而改进后的湍流模型对叶轮内失速引起的旋涡捕捉得更准确,预测精度更高。

(3)以流动稳定性为理论基础,建立更加准确、高效、适合旋转系统下描述泵内部复杂的瞬态湍流流动结构的数学模型,显得尤为重要。

[1] 毕志予, 吴达人. 离心叶轮内二维湍流边界层的数值计算 [J]. 农业机械学报, 1990(1): 83-89. BI Zhiyu, WU Daren. The calculation of 2D turbulent boundary layer in centrifugal impeller [J]. Transactions of the Chinese Society for Agricultural Machinery, 1990(1): 83-89.

[2] 郎涛, 施卫东, 陈刻强, 等. 不同比转数前伸式双叶片离心泵内部流动规律研究 [J]. 农业机械学报, 2015, 46(12): 89-95. LANG Tao, SHI Weidong, CHEN Keqiang, et al. Flow field in forward-extended double blades centrifugal pump at different specific speeds [J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 89-95.

[3] LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence [M]. London, UK: Academic Press, 1972: 157-162.

[4] WILCOX D C. Reassessment of the scale-determining equation for advanced turbulence models [J]. AIAA Journal, 1988, 26(11): 1299-1310.

[5] 杨敏官, 刘栋, 贾卫东, 等. 离心泵叶轮内部三维湍流流动的分析 [J]. 江苏大学学报(自然科学版), 2006, 27(6): 524-527. YANG Minguan, LIU Dong, JIA Weidong, et al. Analysis on turbulent flow in impeller of centrifugal pump [J]. Journal of Jiangsu University (Natural Science Edition), 2006, 27(6): 524-527.

[6] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications [J]. AIAA Journal, 1994, 32(8): 1598-1605.

[7] JOHNSTION J P, HALLEEN R M, LEZIUS D K. Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow [J]. Journal of Fluid Mechanics, 1972, 56(3): 533-557.

[8] IRWIN H P A H, ARONT SMITH P. Prediction of the effect of streamline curvature on turbulence [J]. Physics of Fluids, 1975, 18(6): 624-630.

[9] BRADSHAW P. The analogy between streamline curvature and buoyancy in turbulent shear flow [J]. Journal of Fluid Mechanics, 1969, 36(1): 177-191.

[10]LAUNDER B E, PRIDDIN C H, SHARMA B. The calculation of turbulent boundary layers on spinning and curved surfaces [J]. Journal of Fluids Engineering, 1977, 99(3): 231-239.

[11]KHODAK A, HIRSCH C. Second order non-lineark-εmodels with explicit effect of curvature and rotation [C]∥Proceedings of the 3rd ECCOMAS Computational Fluid Dynamics Conference. New York, USA: Wiley, 1996: 690-696.

[12]HELLSTEN A. Some improvements in Menter’sk-ωSST turbulence model [C]∥Proceedings of the 29th AIAA Fluid Dynamics Conference. Reston, VA, USA: AIAA, 1998: 1-11.

[13]SPALART P R, SHUR M L. On the sensitization of turbulence models to rotation and curvature [J]. Aerospace Science and Technology, 1997, 5: 297-302.

[14]SMIRNOV P E, MENTER F R. Sensitization of the SST turbulence model to rotation and curvature by applying the Spalart-Shur correction term [J]. ASME Journal of Turbomachinery, 2009, 131: 041010.

[15]GÜLICH J F. Centrifugal pumps [M]. Berlin, Germany: Springer, 2007: 85-111.

[16]谈明高, 刘厚林, 袁寿其. 离心泵能量性能预测的对比 [J]. 农业工程学报, 2008, 24(11): 95-98. TAN Minggao, LIU Houlin, YUAN Shouqi. Comparative research on energy performance prediction of centrifugal pumps [J]. Transactions of the CSAE, 2008, 24(11): 95-98.

[17]关醒凡. 现代泵理论与设计 [M]. 北京: 中国宇航出版社, 2011: 600-615.

(编辑 苗凌)

Modification for Turbulence Model Considering Rotation and Curvature with Applications

REN Yun1,2,WU Denghao1,3,MU Jiegang3,LI Xiaojun2

(1. Zhijiang College, Zhejiang University of Technology, Hangzhou 310024, China; 2. School of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China; 3. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Analyzing the problems in the numerical simulation for inner flow by original turbulence model in rotary machines, it is found necessary to totally consider the effects of rotation and curvature for enhancing the numerical accuracy and improving instability of centrifugal pump inner flow. The effects of rotation and curvature ink-ωSST model are taken into account, and a modified turbulence model based on Richardson number from Hellsten is Built. Then the improved turbulence model is adopted to simulate the steady-state inner flow in a centrifugal pump at specific speed of 34.34 under different operating conditions. A comparison between the experimental data and numerical results from the original and modified models reveals the law of pump inner flow. The hydraulic performance predicted by the improved model gets closer to the experimental results than that by original one. In the case of the flow rate of 0.6Qd, the head accuracy and the precision of efficiency predicted by the improved turbulence model increase by 3% and 2%, respectively. The inner flow of pump under 0.6Qdverifies the superiority of the improved turbulence model, and the turbulent flows both in impeller passages and diffusor are improved obviously.

k-ωSST; centrifugal pump; Richardson number; rotation and curvature correction

2016-04-06。作者简介:任芸(1985—),女,讲师。 基金项目:浙江省自然科学基金资助项目(LQ15E090005,LQ15E090004);中国博士后科学基金资助项目(2016M590546);国家自然科学基金资助项目(51409233);浙江工业大学自然科学基金重点资助项目(2014X2015)。

时间:2016-06-14

10.7652/xjtuxb201609004

TH311

A

0253-987X(2016)09-0025-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160614.1715.004.html