一种改进初始中心点的FCM算法

唐德玉，曹东，杨进

（1.广东药科大学医药信息工程学院，广州　510006；2.广州中医药大学医学信息工程学院，广州　510006）

一种改进初始中心点的FCM算法

唐德玉1，曹东2，杨进1

（1.广东药科大学医药信息工程学院，广州510006；2.广州中医药大学医学信息工程学院，广州510006）

传统FCM算法存在聚类初始中心点敏感及迭代次数多的缺点，提出一个改进聚类初始中心点的加强FCM算法。新算法通过数据转换及排序把数据划分到合适的簇中，从而找到最好的聚类初始中心点。在给定聚类数目的条件下，通过UCI机器学习数据库中的两组数据集进行实验比较，结果表明采用加强FCM算法比传统FCM算法收敛速度更快，有较高的准确率和稳定性。

模糊C-均值；目标函数；聚类初始点；数据划分

广东省财政专项“中医药防治重大疾病临床科研信息一体化平台建设项目”、广东省自然基金项(2016A030310300）、基于协同智能优化的药物-靶标相互作用预测方法研究

0　引言

K-Means算法是1967年由Mac Queen提出的聚类算法。K-Means方法是一个划分方法，把数据划分到K个组[1-2]。将模糊数学应用到K-Means算法，从而发展到使用模糊理论的划分方法，也就是目前很流行的模糊C-均值（简称FCM）[7]聚类算法。该算法已经应用在数据挖掘、模式识别、计算机视觉、医学图像等领域，具有重要的理论与实际应用价值。但是K-Means和FCM算法还存在很多共同的问题亟待解决[8]。如聚类数目难确定，初始中心点敏感，迭代次数多，容易陷入局部极值，难以取得全局最优。

针对上述问题，有很多学者提出改进K-Means算法初始中心点的方法[3-6]。而对于FCM算法也出现了很多解决方法。

张慧哲[9]等提出一种计算所有样本点的距离，先找到最近的两个样本点的中心点做为第一个初始中心点，然后根据设置的阈值α，求大于α的所有样本点距离，并求剩下样本点的最小值，做为第二个中心点，重复下去，找到所有初始中心点。

匡泰[10]等人为了解决FCM算法初始点不确定，迭代次数多等问题，提出了基于多项式确定初始中心点的算法，该算法的思想是把类中心看成是多项式的根，通过求多项式的解来确定初始中心点。

还有一些方法，例如采用模拟退火算法进行全局优化，首先产生一个初始解作为当前解，然后在当前解的领域中，以概率P（T）选择一个非局部最优解，并令这个解再重复下去，从而保证不会陷入局部最优。开始时允许随着参数的调整，目标函数偶尔向增加的方向发展，以利于跳出局部极小区域。

也有使用遗传算法提高FCM对高维数据的聚类效果，可以设置遗传算法的适应度函数f=1/（1+J）其中J为FCM目标函数，采用编码方式表示染色体为A= （a1，a2，a3，…，ac），其中ai为一个聚类中心。确定聚类中心数目，群的大小，交叉概率，突变概率，遗传次数，计算隶属度和目标函数，求出适应度函数。循环执行三种遗传操作：复制，交叉，突变。直到最后获得最佳聚类中心。该方法可以获得近似全局解。但其缺点是常常“过早收敛”，不能保证完全获得最优解，而且执行时间比较长。

此外有根据样本点与聚类中心相似关系加权提高FCM准确性的方法，其思想是根据相似性理论，为每一个样本加一个特殊权值让不同的样本在聚类中心中起不同的作用。并对欧氏距离加权。使用合并函数求最大聚类数，其思想是提出一个合并函数，使得（c-1）类的类中心依赖于c类的类中心。保证FCM算法相对稳定，执行速度比普通FCM算法稍快，但不是很明显。给出的方法，算法过于复杂，不适合大数据量应用。

1　传统FCM模糊聚类算法

给定数据集：X={x1，x2，…，xn}，其中每个样本xi包含d个属性。

模糊聚类就是要将X划分为c个类（簇）（2≤c≤n），v={v1，v2，…，vc}为c个聚类中心。在模糊划分中，每一个样本不能严格地被划分到某一类（簇），而是以一定的隶属度属于某一类（簇）。令U=（uij），i=1，2，…，n，j=1，2，…，c为隶属度矩阵。

FCM算法基于求解下面的目标函数的最小值：

其中m是任意一个大于等于2的实数，uij是在j簇中心的隶属度，是第i样本点，vj是簇的中心。

为了获得Jm最小值，运用Lagrange乘数法求极值，得：

对于（1）式，其中vj为第j个聚类中心点，||xi-vj||表示样本点xi到中心点vj的欧氏距离。显然，对于样本点xi到第j个聚类中心vj距离越近，则uij越大。且满足如下条件：

算法的执行步骤如下：

1.初始化U=[uij]矩阵，U（0）.

2.在第k步：使用U（k）计算中心向量V（k）=[vj]，由（2）算得。

3.更新U（k），获得U（k+1）。Uij由公式（1）算得。

2　提出的算法

传统FCM算法是随机产生[0，1]的隶属度矩阵，根据隶属度使用公式（2）找到初始中心点。由于初始中心点是随机产生的，所以传统FCM算法迭代次数比较多，当数据比较多时，算法执行很慢。为此我们提出一个加强FCM（enhancing FCM，以下简称eFCM算法）聚类算法。该方法是找到最好的初始中心点，改进算法的时间复杂度，并提高算法的准确性。

基本思路是计算数据集中所有样本点与样本原点的距离，把数据集中所有样本点与样本原点的距离排序。然后把所有排好序的数据样本点平均划分到K个子集。在这K个子集中的中间样本点做为该集合的初始中心点。这些初始中心点会产生更好的唯一的聚簇结果。排序的算法我们考虑用快速排序算法，因为快速排序算法在最坏和最好情况下，平均时间复杂度为O （NlogN）。

首先我们检查数据集中数据有没有负值[17]，如果数据集中没有负值，那我们不需要数据转换；但如果这个数据集里有负值，那么我们必须把数据集里所有数据的负值转换到正值空间里。转换的方法是先找到数据集中所有属性中的数据的最小值（负值），然后让数据集中所有数据减去最小值。这个转换是必须的，因为我们提出的这个算法，就是要计算数据集所有样本点与坐标样本原点的距离。对于不同的数据样本点，我们可以获得几乎不同的距离。如图1中a），可以看出在二维空间中四个点（x1，y1），（x2，y2），（x3，y3），（x4，y4）在四个象限中，四个点与原点（0，0）的距离几乎相等；而数据进行转换后，四个点全部放在第一象限。此时，四个点与原点（0，0）的距离明显不同。

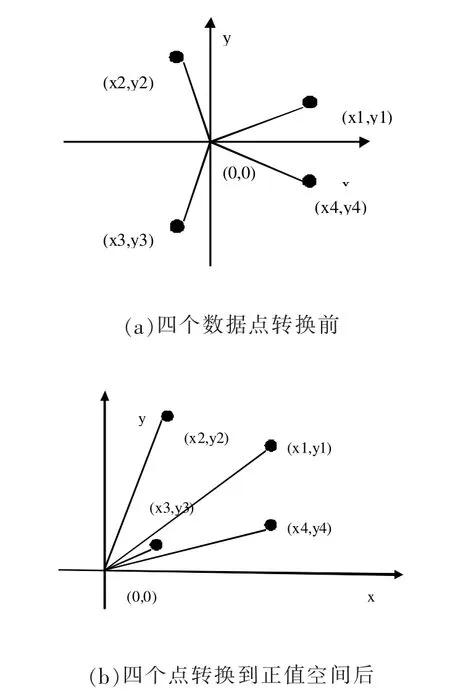
图1　数据转换

虽然欧氏距离对球形结构聚类有一定的优势，但在解决高纬数据问题时，存在一些计算上的弊端。而马氏（Mahalanobis）距离计算仅涉及协方差矩阵的求逆，不再和特征矢量的维数有关，而是和样本数目有关，因此在高纬特征空间中带来计算上的优势，在无穷维特征空间中解决了计算上存在的问题。所以我们在进行数据划分时，采纳马氏距离计算样本原点与数据样本的距离，然后平均划分为K个子集。

下一步，求初始中心点。加强FCM算法步骤如下：

输入：

D={x1，x2，x3，…，xi，…，xm}//m个样本数据点

d={d1，d2，d3，…，di，…，dn}//一个样本数据点的n个属性k//需要的簇的数目

输出：k个初始中心点

步骤如下：

1.给定的数据集D，如果包括负值和正值的属性值，那么程序跳转到2，否则跳转到4。

2.找到数据集D中属性值的最小值。

3.数据集D中的所有数据点的值减去最小值。

4.使用马氏距离计算所有样本点与样本原点的距离。

5.根据第4步获得的距离进行排序。

6.把排好序的数据点分成K个相等的子集合。

7.在每个子集中找到离样本原点距离为中等的样本点做为该子集的聚类初始中心点。

8.根据获得的聚类初始中心点使用公式（1）计算隶属度。

9.根据获得的隶属度使用公式（2）计算新的聚类中心点。

10.计算目标函数值，并计算误差，如果误差小于阈值，程序结束。否则跳到8。

3　仿真模拟实验

为了验证提出的算法的有效性和准确性，我们使用UCI机器学习中的Iris和Wine数据进行仿真实验，然后对传统FCM算法和eFCM算法进行比较。实验源数据表如表1：

表1　数据源信息

本文实验环境是，处理器频率为2.10GHz，内存3G，硬盘120G，使用Windows XP 32位操作系统。开发工具使用MATLAB 7.8。实验初始化参数如下：隶属度指数expo=2.0，簇数目clustern=3，迭代最大数目maxiter=100，目标函数值误差最小阈值为minimpro=1e-6。我们对Iris和Wine数据先对归一化处理，以减少量纲不同对算法的影响。使用公式Y=（Ymax-Ymin）*（X -Xmin）/（Xmax-Xmin）+Ymin，X为数据原始样本值，Y为数据规范化后的数据，我们使用Ymin=0，Ymax=1，使所有数据落在[0，1]范围内。

为了保证实验的准确性，我们对传统FCM算法做了7次实验，计算算法的迭代次数，运行时间及准确率的平均值。而对eFCM算法做了7次实验，计算运行时间的平均值。

表2　传统FCM算法与eFCM算法的比较

从表2中结果可以看出，我们提出的eFCM算法的准确率高于普通FCM算法。Iris数据集和Wine数据集都有类标号，每个数据集分为3个类（簇）（见表1）。准确性的计算就是用聚类算法产生的三个簇中的样本与已知的三个类（簇）中的样本类别进行比较，计算聚类产生的簇中正确分类的样本总数。准确率=同一簇中正确分类的样本总数/同一簇已有样本总数。比如，见表3，对于Iris数据集中的分类1（簇1），同一簇已有样本总数=50，FCM聚类产生的同一簇中正确分类的样本总数=46，其准确率为46/50约为92%;eFCM聚类产生的同一簇中正确分类的样本总数=50，其准确率为50/50等于100%。总的准确率=所有簇中正确分类的样本总数/所有簇中已有样本总数（见表2）。

对于模糊C-Means算法而言，目标值越小，说明聚类的越好。传统FCM算法产生的第一个初始聚类中心点与稳定后的聚类中心点有很大偏离；eFCM算法产生的第一个初始聚类中心点与最后的聚类中心点接近，所以目标值也很小。对于IRIS数据集中从图2和图3可以看出，FCM算法产生的第一个目标值（4.5112），而eFCM算法的第一个目标值（0.6811）。对于Wine数据集中，FCM算法产生的第一个目标值（0.21），而eFCM算法的第一个目标值（0.0843）。这也说明eFCM算法选择的初始中心点的有效性。加强的eFCM算法比传统的FCM算法相比，数据样本分类的准确率有所提高，簇与簇之间的分类清晰，簇内数据样本更加紧凑，聚类效果更好。如表3可见eFCM算法对3个类正确分类的能力有提高。

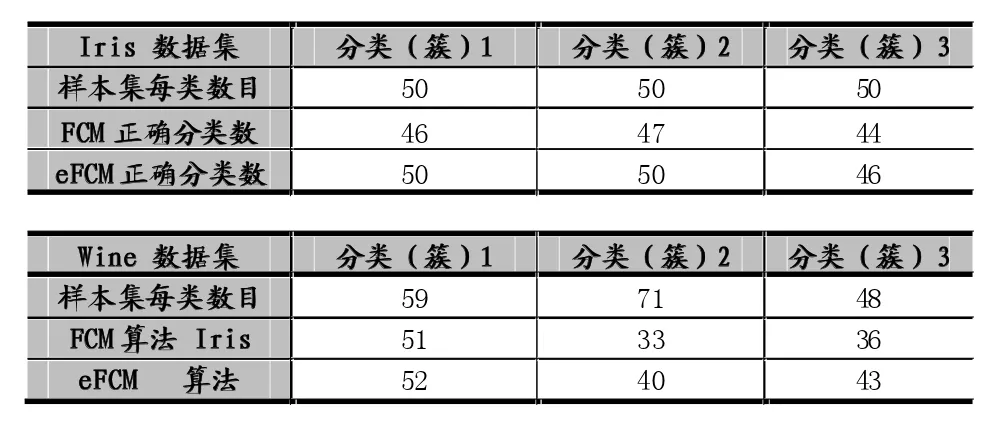
表3　传统FCM算法与eFCM算法的比较

特别是eFCM算法的运行速度很快。对于Iris数据加强FCM算法只需要迭代7次，而传统FCM算法要迭代15次；对于Wine数据，eFCM算法只需要迭代12次，而传统FCM算法要迭代20次。使用MATLAB画图显示了两个算法目标函数的迭代情况。如图2和图3。

图2　Iris数据FCM算法和eFCM算法的迭代情况

图3　Wine数据FCM算法和eFCM算法的迭代情况

最后，我们对于传统FCM和eFCM算法的时间复杂度进行分析，对于传统FCM算法来说，最大迭代次数需要循环maxiter次，隶属度计算需要执行clustern*datan*datam次循环，中心点计算也要执行clustern*datan*datam次循环，目标函数是计算所有样本与中心点的距离，要执行clustern*datan*datam次循环。所以总的执行时间为O（maxiter*clustern*datan*datam）。而目标函数的误差值小于指定最小值时，程序可以在小于maxiter次循环停止。由于传统FCM算法初始中心点是随机产生的，所以要找到最佳的聚类中心点，迭代次数一般都比较多，很多情况下是要maxiter次迭代，而这是循环执行最多的情况。而对于我们提出的eFCM算法在执行时间要O（miniter*clustern*datan *datam），其中miniter<

4　结语

FCM算法也是目前很流行的聚类算法，但FCM算法由于初始中心点是随机产生的，使得FCM算法执行比较慢，准确性也有所降低。我们提供的eFcm算法与传统FCM算法相比，更加高效和准确。该方法找到最好的初始中心点，把所有的样本数据点分配到合适的簇中。而这个数据划分机制所需要时间复杂度仅为O （NlogN），eFCM算法的时间复杂度为O（miniter*clustern*datan*datam），miniter<

[1]A.M.Fahim，A.M.Salem，F.A.Torkey，M.A.Ramadan.An Efficient Enhanced K-Means Clustering Algorithm.Journal of Zhejiang University，10（7）:1626-1633，2006.

[2]K.A.Abdul Nazeer，M.P.Sebastian.Improving the Accuracy and Efficiency of the K-Means Clustering Algorithm.In International Conference on Data Mining and Knowledge Engineering（ICDMKE），Proceedings of the World Congress on Engineering（WCE-2009），Vol 1，July 2009，London，UK.

[3]Chen Zhang，Shixiong Xia.K-Means Clustering Algorithm with Improved Initial Center.in Second International Workshop on Knowledge Discovery and Data Mining（WKDD），pp.790-792，2009.

[4]F.Yuan，Z.H.Meng，H.X.Zhangz，C.R.Dong.A New Algorithm to Get the Initial Centroids.Proceedings of the 3rd International Conference on Machine Learning and Cybernetics，pp.26-29，August 2004.

[5]Koheri Arai,Ali Ridho Barakbah.Hierarchical K-Means:an Algorithm for Centroids Initialization for K-Means.Department of Information Science and Electrical Engineering Politechnique in Surabaya，Faculty of Science and Engineering，Saga University，Vol.36，No.1，2007.

[6]S.Deelers and S.Auwatanamongkol.Enhancing K-Means Algorithm with Initial Cluster Centers Derived from Data Partitioning along the Data Axis with the Highest Variance.International Journal of Computer Science，Vol.2，Number 4.

[7]Bezdek J C.Pattem Recogition with Fuzzy Objective Function Algorithms[M].NY:Plenum，1981.

[8]Duda R，HartP，Stork D.Pattern Classification（2 nd Edition）[M].New York，USA;John Wiley&Sons，2001.

[9]张慧哲.基于初始聚类中心选取的改进FCM聚类算法[J].计算机科学，2009，26（6）；206-209.

[10]匡泰.FCM算法用于灰度图像分割的初始化方法的研究[J].计算机应用，2006，26（4）；784-786.

The traditional FCM algorithm has the defection of sensitivity to the initial cluster center and iterate so more,proposes an enhancing FCM algorithm by improved cluster initial center.A novel algorithm can partition data set into suited clusters through data conversion and sorting,and then find a best initial center.Given the number of cluster,test and compare by two group data set of UCI machining study database,results demonstrate that enhancing FCM algorithm has fast convergence,enhancing accuracy and stability than traditional FCM. Keywords：

Fuzzy C-Means;Objective Functiong;Initial Cluster Center;Data Partitioning

A FCM Algorithm Based on Improved Initial Cluster Center

TANG De-yu1，CAO Dong2，YANG Jin1

（1.Guangdong Pharmaceutical University，College of Medical Information and Engineering，Guangzhou 510006；2.Guangzhou University of Chinese Medicine，Guangzhou 510006）

唐德玉（1978-），男，广东广州人，博士，副教授，研究方向为数据挖掘、智能计算、网络集成

曹东（1975-），男，博士，副院长

杨进（1977-），男，广东广州人，硕士，讲师，研究方向为数据挖掘、智能计算

2016-09-13

2016-10-20