基于数据挖掘技术的污泥厌氧消化模拟研究

李 佟， 李 军

(1.北京工业大学建筑工程学院， 北京 100124；2.北京城市排水集团有限责任公司， 北京 100124)



基于数据挖掘技术的污泥厌氧消化模拟研究

李 佟1,2， 李 军1

(1.北京工业大学建筑工程学院， 北京 100124；2.北京城市排水集团有限责任公司， 北京 100124)

为了更好地模拟实际工程中污泥厌氧消化系统的产气效果，以北京某大型污泥厌氧消化工程为例，以大量的工程数据为基础，分别采用多元线性回归模型、神经网络模型、分类回归模型和邻近算法模型等数据挖掘技术，对系统的产沼气效率进行了模拟预测,其中邻近算法模型具有最好的拟合效果. 对邻近算法模型进行进一步研究分析,通过交叉验证法近一步优化了模型k值的选取,从测试结果可以看出随着k值增加，训练集的拟合度先下降后趋于平稳，测试集的拟合度则相反. 最终确定当k值取5时，模型预测值与实际值的相关度达0.862，优于系统默认参数下的拟合效果. 试验证明：数据挖掘技术可以很好地应用于污泥厌氧消化工程的模拟计算,对于数学模拟在污水处理领域的应用具有一定指导意义.

数学模型；数据挖掘；k最邻近算法；污泥厌氧消化

污泥厌氧消化是指兼性菌和厌氧菌在无氧条件下将污泥中的可生物降解有机物分解成二氧化碳、甲烷和水的过程[1-2]，因其具有减少污泥体积、杀灭病原细菌、改善污泥脱水性能、产生沼气能源等优点，所以作为城镇大型污水处理厂的主流工艺一直被广泛应用. 由于污泥厌氧消化过程包含了生物、化学、物理等各种复杂反应[3]，因此要对其进行完全精准的数学模拟有很大难度.

目前国内已有的相关研究大多是建立在机理模型基础上的，例如周芳[4]利用国际水协的厌氧消化1号数学模型(ADM1)，对郑州王新庄污水处理厂厌氧消化工程运行进行了模拟研究，取得了较好的效果. 然而在实际工程运行中，整体系统的最终运行效果是由多方面因素综合作用而成的，机理模型并未将生物反应以外的影响因素考虑在内，因此在一定程度上会造成偏差.

数据挖掘技术是一种很好的数据分析手段，已被广泛应用于生物信息学、制造业和能源等工程科技领域[5-8]，国外已有一些针对厌氧消化过程的数据挖掘应用研究[9-11]. 例如Cakmakci[12]将自适应模糊神经网络系统(adaptive neuro-fuzzy inference system)应用于污水处理厂污泥厌氧消化模拟预测，并取得了很好的效果；Holubar等[13]通过BP神经网络模拟预测厌氧消化过程中的沼气产率，并通过测定沼气中甲烷的质量分数、产气速率、pH、挥发性悬浮物(volatile suspended solids，VSS)质量浓度等参数，得出了实现最大产气量的工艺控制策略，而国内在这方面的研究还比较少.

本文以北京某大型污泥厌氧消化工程为例，以大量的工程数据为基础，摸索采用数据挖掘技术对厌氧消化工艺过程进行模拟研究. 在本研究中，笔者分别采用了多元线性回归模型、神经网络模型、分类回归模型和邻近算法模型等数据挖掘技术，对厌氧消化系统的产沼气效率进行了模拟预测. 通过对比，找出了具有最好拟合效果的模型，并通过交叉验证法近一步优化了该模型的参数取值，使得该模型有了更好的拟合效果.

1 污泥厌氧消化工程

1.1 污泥厌氧消化工程介绍

本研究在北京某大型污水处理厂内开展，该厂设计污水处理能力100万m3/d，其污泥处理部分采用中温两级厌氧消化工艺，消化后的污泥经脱水后再进一步处置，消化产生的沼气主要用于发电，沼气发电机的热水又可作为消化污泥加热的热源回收利用，具体工艺流程图及设计参数如图1和表1所示.

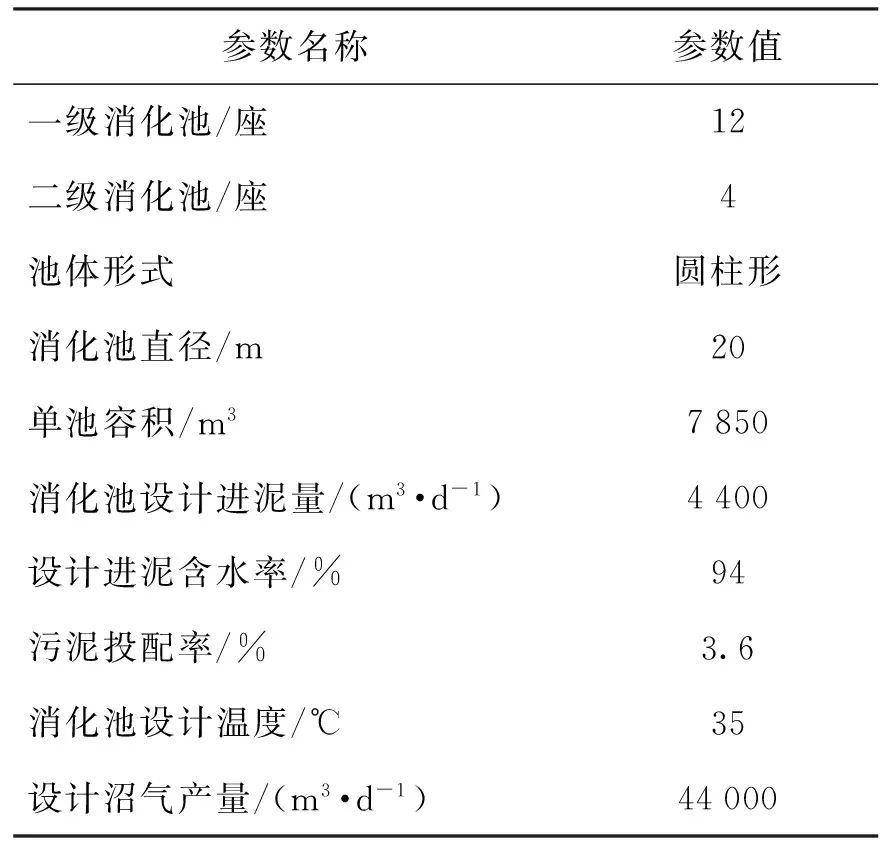
参数名称参数值一级消化池/座12二级消化池/座4池体形式圆柱形消化池直径/m20单池容积/m37850消化池设计进泥量/(m3·d-1)4400设计进泥含水率/%94污泥投配率/%3.6消化池设计温度/℃35设计沼气产量/(m3·d-1)44000

1.2 厌氧消化基本原理

有机物的厌氧消化过程，即在特定的厌氧条件下，在兼性厌氧菌、专性厌氧菌等微生物的共同作用下，有机质被生物降解成CH4和CO2的过程，厌氧消化又被称为厌氧发酵. 根据不同类别微生物作用类型和阶段，厌氧消化反应过程又被划分为不同的阶段. 一般认为，厌氧消化的总过程被分为水解、发酵、产氧产乙酸以及产甲烷4个阶段.

厌氧消化系统中的微生物种类繁多，主要分为产甲烷菌和非产甲烷菌两大类，它们彼此之间关系复杂，既有互利共生关系也有竞争关系，但正是由于各种微生物相互协同，彼此之间发生着一系列的生物化学偶联反应，才最终产生了甲烷. 影响厌氧消化系统的因素非常多，例如温度、厌氧环境、pH、脂肪酸等条件的变化，都会对厌氧消化产甲烷效果产生影响.

1.3 运行数据及参数分析

本研究所用数据取自该厂2013年1月1日至12月31日的实际生产数据，共计365组. 每组数据包含10个参数，其中有进泥量、温度、含水率、脂肪酸等8个测量值和有机负荷、停留时间等2个计算值，具体见表2.

从表2可以看出，消化系统的进泥量和沼气产量变化范围非常大，这是因为该时期内因工艺调整，消化系统经历了短暂的停运和恢复启动过程，这恰好为系统建模提供了更加全面良好的训练数据样本.

表2中包含了厌氧消化工艺运行中常用的几种主要控制参数. 厌氧微生物对温度变化非常敏感，温度稍有波动便会对系统产生不良影响，造成产气量的下降. 因此，在厌氧消化过程中，保持温度稳定非常重要；挥发性脂肪酸(volatile fatty acids，VFA)是厌氧消化过程中重要的中间产物，大部分沼气是由VFA在产甲烷菌的作用下形成的，消化过程中VFA过高或过低都会对系统产生不利影响，因此出泥VFA是厌氧系统重要的控制指标之一；有机负荷是由进泥量、进泥含水率等指标计算而得，它反映了厌氧消化系统处理有机物的能力，对系统运行效率和稳定性都有重要影响.

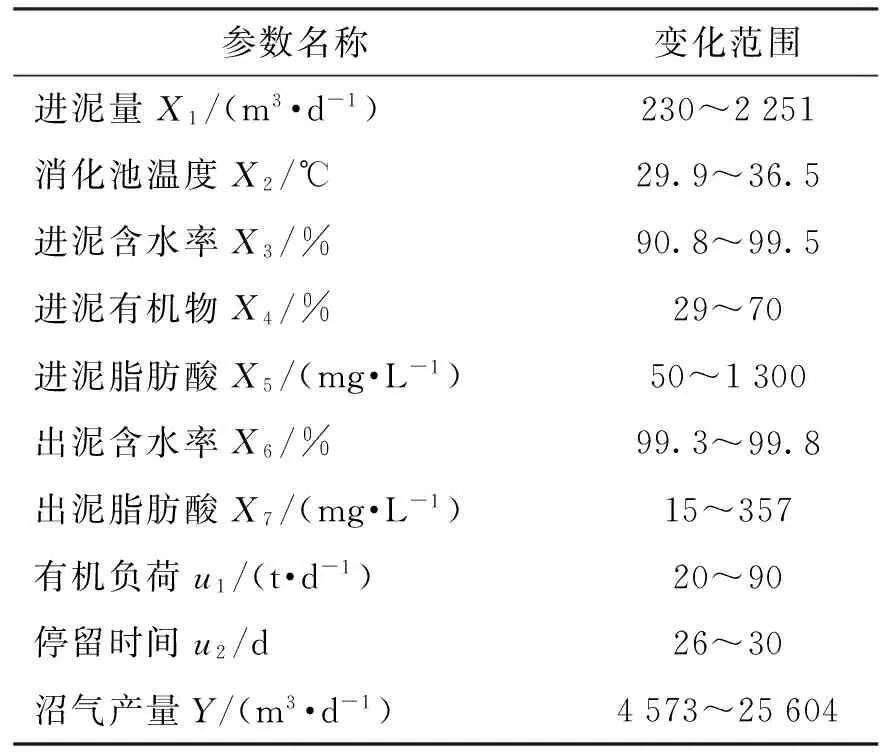
表2 消化系统主要工艺参数及化验数据

除以上指标外，影响厌氧消化运行效果的因素还有很多，例如pH、碱度、氨氮、基质营养比例、基质颗粒尺寸、沼气组分、消化池搅拌效果等. 这其中很多指标对于建立机理模型来说是必不可少的，但在实际工程中却并没有积累大量数据可供利用. 而数据挖掘技术的优势之一便是无须掌握所有参数，只要利用现有数据便可建立与目标的关系模型，这非常适用于实际工程.

2 基于数据挖掘技术的模拟预测

2.1 模拟工具

本研究计算工具采用IBM公司开发的SPSS MODELER软件，它提供了一组功能强大的数据挖掘工具，包括各种借助机器学习、人工智能和统计学的建模方法. 主要功能包括对数据进行预处理、训练、模型评估、预测、误差分析等，具有界面友好、兼容性强、数据处理方法丰富等优点.

2.2 数据挖掘模型介绍

本研究分别采用多元线性回归、神经网络、分类回归树和邻近算法等4种最常用的模型来进行分析对比.

2.2.1 多元线性回归模型(multivariable linear regression model，MLR)

该模型是以统计学为理论基础，用2个或2个以上的变量来解释因变量的一种模型，是多元统计分析中的一个重要方法，被广泛应用于众多自然科学领域的研究中.

多元线性回归模型的建立：

假设某一因变量y受k个自变量x1,x2,…,xk的影响，其n组观测值为(ya,x1a,x2a,…,xka)，a=1,2,…,n. 那么，多元线性回归模型的结构形式为

ya=β0+β1x1a+β2x2a+…+βkxka+εa

(1)

式中：β0,β1,…,βk为待定参数；εa为随机变量. 如果b0,b1,…,bk分别为β0,β1,…,βk的拟合值，则回归方程为

(2)

式中：b0为常数；b1,b2,…,bk称为偏回归系数.

2.2.2 神经网络模型(neural networks，NN)

该模型是由大量的、简单的处理单元(称为神经元)广泛地互相连接而形成的复杂网络系统，是一个高度复杂的非线性学习系统，具有大数量、分散性存储和处理、自组织、自适应和自学能力，特别适合处理要包含很多影响因子的条件的过程，并且适合信息量很大的数据处理过程.

神经元是一个多输入单输出的信息处理单元，它对信息的处理是非线性的. 根据神经元的特性和功能，可以把神经元抽象为一个简单的数学模型，如图2所示.

图2中X1，X2，…，Xn是神经元的输入，即来自前级n个神经元的轴突的信息；Σ是i神经元的阈值；Wi1，Wi2，…，Win分别是i神经元对X1，X2，…，Xn的权系数，也即突触的传递效率；Yi是i神经元的输出；f[·]是激发函数，它决定i神经元受到输入X1，X2，…，Xn的共同刺激达到阀值时以何种方式输出.

从神经元模型可以得到神经元的数学模型表达式为

(3)

2.2.3 分类回归树算法(classification and regression tree，C&RT)

该模型是基于统计理论的非参数的识别技术，具有非常强大的统计解析功能，而且处理后的结果所包含的规则明白易懂. 它的主要原理是利用了二叉树的结构特点，使根节点包含全部样本，并且按照规定的规则，将根节点分割为2个子节点，以此类推在子节点上继续重复进行，成为一个回归过程，直至不可再分成为叶节点为止.

假设样本空间X包含2类样本(A、B类)，C&RT将之作为根节点，按照一定规则进行分割，产生2个节点，即子集X1、X2满足X=X1∪X2，且X1∩X2=∅. 这个过程回归地对X1、X2重复进行，直至按照某种标准，节点无法再分，成为最终的叶节点，而这些叶节点所表示的数据子空间的特征决定了它们属于哪一类样本(A或B类). 在同一棵树上，若干叶节点可以有相同的类别标志，故最终的分类结果是相同类别标志的叶节点的并集，最终整个空间X=XA∪XB，如图3所示.

2.2.4 邻近算法(k-nearest neighbor，kNN)

该模型是一个应用较为广泛，原理和技术比较成熟的算法，同时相对于其他模型也更为简单易懂. 其基本原理是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性，具体的算法步骤如下：

1) 根据特征项集合描述训练数据.

2) 在新数据进入后，根据特征向量确定新数据的向量表示.

3) 在训练数据集中选出与新数据最相似的k个数据，计算公式为

(4)

式中k值的确定目前没有很好的方法，一般采用先定一个初始值，然后根据实验测试的结果调整k值，一般初始值定为几百到几千之间.

4)在新数据的k个邻居中，依次计算每类的权重，计算公式为

(5)

2.3 模型参数设置

为了取得满意的模拟效果，就必须对每种模型进行参数设置. 本研究首先需要选定一个适用的模型，在此过程中所有模型设置都采用系统默认参数，在选定适合模型后，再对该模型的参数进行近一步优化设置，本研究中4种模型的部分参数设置值见表3.

2.4 模拟结果分析

采用该厂稳定运行一年的365组数据，将数据分为训练集和测试集，其中255组数据用于模型的训练，110组数据用于模型验证，4种模型的拟合结果分别见图4～7.

从图中可以看出，采用4种模型均能较好地模拟厌氧消化的产气过程，为了更好地评价各模型的应用效果，分别统计计算各模拟结果的平均绝对误差(MAE)、标准差(MSE)和相关系数(Correlation coefficient)(见表4).

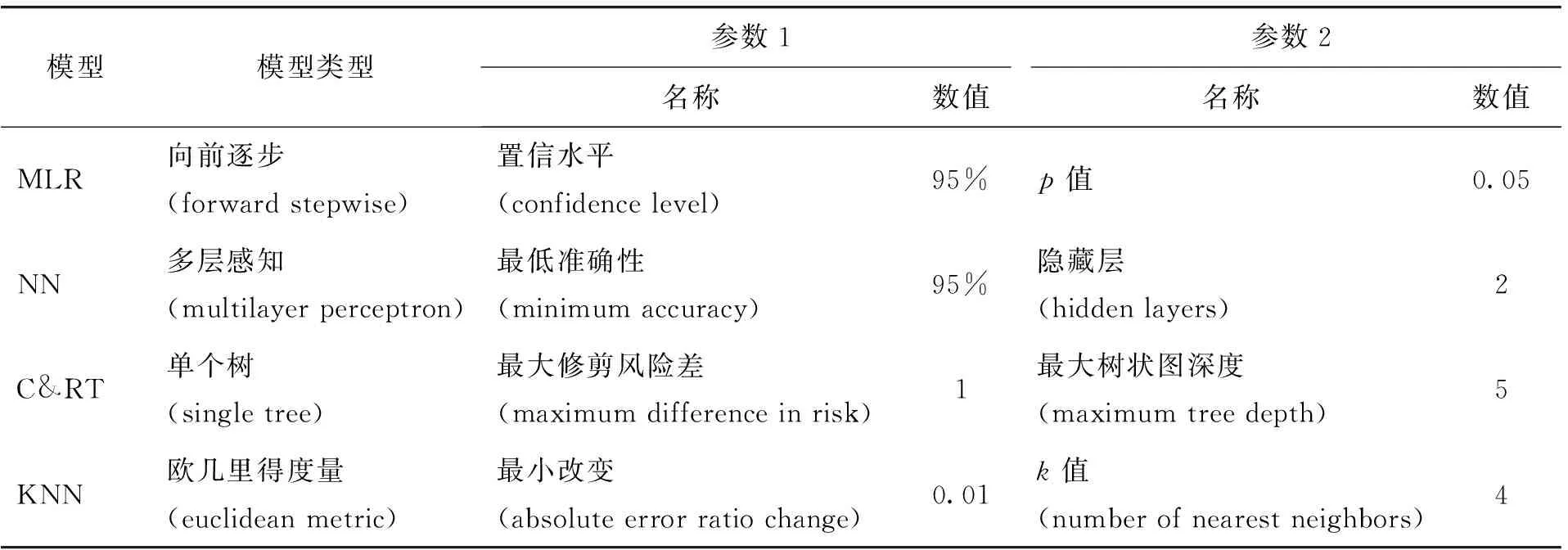
表3 模型设置参数

从表4可以看出，4种模型模拟结果的平均绝对误差在1 553～1 940，相对误差在12.7%～10.1%，其中除MLR算法外，其余算法与实际沼气产量的误差均为±10%. 从工艺控制角度看，系统受生物反应速率、仪器仪表精度以及各种其他外部条件影响，很难完全达到预期的调控值. 结合笔者的实际经验，认为10%的模拟误差在工艺控制和工程上都是可以接受的.

从各误差值及相关系数综合来看，MLR模型的准确率最低，kNN模型最高. 下面则以kNN模型为例进行进一步分析研究.

kNN分类法的具体算法及实现步骤为：

表4 4种算法的模拟误差对比

1) 构建分类结构体系，设定相应的类别，在本例中共包含进泥量、进泥含水率、进泥有机物、进泥脂肪酸、出泥含水率、出泥脂肪酸、消化池温度、沼气产量等8类指标.

2) 针对当前待分类别特点，优选对象特征，通过逻辑运算符将选取特征组合，建立特征空间，如图8所示.

3) 对于当前待分类别，不同类别交互式选取相应的训练样本，在特征空间中逐一计算待分类对象与类别的最小距离.

在实际厌氧消化工程运行中，系统绝大部分时期是处于稳定状态的，其沼气产量的变化并不大，只有当运行异常时，才会产生较大的波动. 因此，污泥厌氧消化样本的相近或重复很多. 而kNN模型的算法驱动主要是靠目标样本周围的邻近样本特征而定的，并非采用判别类域等方法，因此对于上述样本近似或重复的情况来说，kNN模型具有一定的优势.

2.5 kNN模型参数优化

kNN算法的k值选择将直接影响模拟结果，因为kNN算法的核心思想是如果一个样本在特征空间中的k个最相似的样本中的大多数属于某个类别，则该样本也属于这个类别，即k代表了所要选取的最相似样本的个数.k选择过小，得到的近邻数过少，会降低分类精度，同时也会放大噪声数据的干扰；k选择过大，在选择k个近邻的时候，并不相似的数据亦被包含进来，造成噪声增加而导致分类效果的降低.

对于k的选择，一般依靠经验或者交叉验证(一部分样本做训练集，一部分做测试集). 在本研究中，采用k值交叉验证的方法来确定最佳参数，即初始取一个比较小的k，通过不断调整k的大小来找出最优化的分类，此时得到的k就是最佳参数. 在测试时，一般k取奇数为佳.

测试结果如图9所示，可以看出随着k值增加，训练集的拟合度先下降后趋于平稳，测试集的拟合度则相反.kNN的模型复杂度主要由k决定，k值越小，复杂度越高，训练准确度越高，但过度拟合的模型并不能保证实际测试的准确率也高. 一般来说，测试集的准确率在模型过复杂和过简单时都比较低，唯有通过试验才能选出最适合的值. 在本例中，当k取5时，测试集相关度为0.862——优于系统默认参数(k=4)下的模拟效果，因此最终模型k取5.

3 结论

1) 本文研究了数据挖掘技术在污泥厌氧消化工程中的实际应用，分别采用多元线性回归模型、神经网络模型、分类回归模型和邻近算法模型对污泥厌氧消化的产气效果进行了模拟预测，结果表明数据挖掘技术可以很好地应用于污泥厌氧消化过程模拟，具有一定实际应用价值.

2) 通过对4种模型的误差对比分析可以看出，采用kNN算法模拟污泥厌氧消化过程具有更好的精度和准确性. 该算法对于类域的交叉或重叠较多的待分样本集来说，较其他方法更为适合，这符合实际厌氧消化工程运行的数据样本特点.

3) 通过交叉验证法对kNN模型的参数进行近一步优化，确定k取5时的模拟效果最优化. 而应用于其他数据样本时，还需对k参数值的选取进行重新评估.

[1] LETTINGA G. Anaerobic digestion and wastewater treatment systems [J]. Biomedical and Life Sciences, 1995, 67(1): 3-28.

[2] 任南琪. 厌氧生物技术原理与应用[M]. 北京: 化学工业出版社, 2004: 23-24.

[3] BATSTONE D, KELLER J, ANGELIDAKI I, et al. The IWA anaerobic digestion model No1 (ADM1) [M]. Queensland: Water Science and Technology, 2002: 65-73.

[4] 周芳. 应用厌氧消化模拟技术对某污水厂消化池运行的分析[D]. 天津：天津大学, 2014. ZHOU FANG. Analysis on the operation of an anaerobic digester in a wastewater treatment plant with the anaerobic digestion simulation[D]. Tianjin: Tianjin University, 2014. (in chinese)

[5] KUSIAK A, LI M Y. Cooling output optimization of an air handling unit [J]. Applied Energy, 2010, 87(3): 901-909.

[6] FRANK E, HALL M, TRIGG L, et al. Data mining in bioinformatics using Weka[J]. Bioinformatics, 2004, 20(15): 2479- 2481.

[7] KUSIAK A, ZHENG H Y, SONG Z. Wind farm power prediction: a data-mining approach [J]. Wind Energy, 2009, 12(3): 275-293.

[8] SECKIN N. Modeling flood discharge at ungauged sites across Turkey using neuro-fuzzy and neural networks [J]. Journal of Hydroinformatics, 2011, 13(4): 842-849.

[9] SCHUBERT J, SIMUTIS R, DORS M. Bioprocess optimization and control: application of hybrid modeling [J]. Journal of Biotechnology, 1994, 35(1): 51-68.

[10] TAY J H, ZHANG X. Neural fuzzy modeling of anaerobic biological wastewater treatment systems [J]. ASCE Journal of Environmental Engineering, 1999, 125(12): 149-159.

[11] SOTEMANN S W, RISTOW N E, WENTZEL M C, et al. A steady state model for anaerobic digestion of sewage sludge [J]. Water S A, 2005, 31(4): 511-527.

[12] CAKMAKCI M. Adaptive neuro-fuzzy modeling of anaerobic digestion of primary sedimentation sludge [J]. Bioprocess and Biosystems Engineering, 2007, 30(5): 349-357.

[13] HOLUBAR P, ZANI L. Modeling of anaerobic digestion using self-organizing maps and artificial neural networks[J]. Water Science and Technology, 2000, 41(12): 149-156.

(责任编辑 吕小红)

Simulation Research of Sewage Sludge Anaerobic Digestion Based on Data Mining Technology

LI Tong1,2, LI Jun2

(1.College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2. Beijing Drainage Group CO., LTD., Beijing 100022, China)

This research was based on a large sludge anaerobic digestion project in Beijing, using a large number of engineering data. The multiple linear regression model, the neural network model, the classification and regression model andknearest neighbor model to was adopted fit the system biogas production to simulate the biogas production of sluge anaerobic digestion system in practical engineering. Results show that the kNN model has the best fitting effect. For further kNN model analysis, cross validation error statistics selection method was used to determin the bestkvalue. From the test results, it can be seen that with the increase ofkvalue, the fitting degree of the training set first decreases and then tends to be stable, and the fitting degree of the test set was the opposite. Finally, when thekvalue was 5, the correlation between the model predictive value and the actual value was 0.862, which is better than the fitting effect of the system’s default parameters. The research shows that the data mining technology can be applied to the simulation of sludge anaerobic digestion very well, and has certain guiding significance for the application of mathematical simulation in the field of wastewater treatment.

mathematical model; data mining;knearest neighbor algorithm; sludge anaerobic digestion

2015- 07- 23

国家水体污染控制与治理科技重大专项资助项目(2014ZX07201- 001)

李 佟(1982—)， 男， 工程师， 主要从事污水深度处理、污水处理模拟技术等方面的研究， E-mail: ltong@bdc.cn

U 461；TP 308

A

0254-0037(2016)12-1888-07

10.11936/bjutxb2015070092