基于序列二次规划算法的点阵夹芯结构优化设计
2016-12-22龙连春刘金坡王鲲鹏
龙连春, 薛 飘, 刘金坡, 王鲲鹏, 谭 指
(1.北京工业大学机械工程与应用电子技术学院, 北京 100124;2.北京宇航系统工程研究所, 北京 100076)
基于序列二次规划算法的点阵夹芯结构优化设计
龙连春1, 薛 飘1, 刘金坡1, 王鲲鹏2, 谭 指2
(1.北京工业大学机械工程与应用电子技术学院, 北京 100124;2.北京宇航系统工程研究所, 北京 100076)
为了研究夹芯单胞变化对结构承载能力的影响,建立了点阵夹芯结构的优化设计模型,以结构刚度最大为目标函数,考虑体积约束及单胞尺寸约束对夹芯单胞尺寸分布进行优化设计,并以四面体单胞夹芯结构的优化设计为例进行详细方法说明. 采用序列二次规划法求解优化模型,完成了以结构刚度最大为目标的井字梁夹芯结构的优化设计,验证了模型、方法及优化效果.
点阵夹芯结构;四面体单胞;序列二次规划算法
点阵夹芯结构是近年来随着材料制备工艺和成型加工技术的发展而出现的一类新型多功能材料结构,它由2块面板和夹于面板之间的超静定的点阵夹芯构成,由于它具有超轻质、高比强度、高比刚度、高能量吸收等优良机械性能,以及减震、散热、吸声、电磁屏蔽等特殊性质,成为了一种备受瞩目的性能优异的多功能性工程材料结构. 2001年,Evans等[1]提出了点阵夹芯结构概念;同年,Wicks等[2]分析对比了三角形桁架、实体材料、四面体单胞夹芯结构,结果表明,材料相同的前提下,点阵夹芯结构具有更高的质量效率. 点阵夹芯结构常用单胞有正四面体单胞[3]、金字塔单胞和Kagome单胞等. 正四面体单胞点阵夹芯材料刚度和强度都较高,且有着较轻的质量,同时由于面板的存在使得材料结构在多种静力学、动力学等复杂载荷作用下均具有优良性能[4]. Kooistra等[5]对四面体单胞夹芯结构进行了压缩实验研究,结果表明,在相同质量下,四面体单胞夹芯板的承载能力优于加强筋板以及泡沫夹芯板,并认为夹芯面板失效模式与芯子的拓扑结构以及材料的屈服应变有关. Chiras等[6]研究了四面体单胞夹芯结构在剪切、弯曲和压缩载荷下的力学性能,发现在面内剪切载荷作用下结构呈现出不对称性的特点. 在弯曲载荷作用下,因芯子半径的不同发生的破坏模式有明显差异. 半径较小时,结构以剪切失效为主;半径较大时,主要在面板部位发生屈曲. Wicks等[7]对二维桁架夹芯结构在纯弯曲载荷作用下进行了优化设计. Chen等[8]采用低速动力压缩试验,揭示了多层夹芯板的失效机理和能量吸收能力,用动力屈曲理论解释了结构的应变率效应. Dahiwale等[9]研究了点阵夹心结构中夹心的高度和上下面板的厚度对结构刚度的影响. 隋允康等[10]提出了将设计变量分为2层来求解桁架结构形状优化的方法. 汪浩等[11]以轻质金字塔点阵夹层平板结构为对象,对其在不同撞水速度下的流- 固耦合动力学行为进行数值和理论计算分析,指出与同等质量实体板相比,轻质金字塔点阵夹层板最大变形均显著降低. 泮世东等[12]为了提高金字塔单胞夹芯结构的整体等效剪切强度,对面外剪切载荷作用下的金字塔单胞夹芯结构进行了优化设计,提高了金字塔单胞夹芯结构的整体等效剪切强度. Hyun等[13]在平压剪切载荷工况下,利用有限元方法研究了Kagome单胞夹芯板和四面体单胞夹芯板的性能.
综上所述,在新型单胞夹芯结构研究方面,国内外已经开展了广泛的研究工作,在数值模拟与实验测试方面做了大量工作,但对于点阵夹芯结构的优化工作还需进一步的深入.
1 点阵夹芯结构优化设计模型及求解方法
1.1 点阵夹芯结构的参数化构造
在对点阵夹芯结构进行优化时,首先对其结构进行参数化构造. 点阵夹芯结构由上下基板和夹芯层组成,由于上下基板的尺寸与整体结构尺寸有关,其长、宽、厚等尺寸根据结构的外形尺寸确定. 其夹芯层的结构及尺寸则与所选择的单胞形状与尺寸有关.
这里选用四面体单胞夹芯结构进行参数化构造与优化设计. 四面体单胞及夹芯板如图1所示. 四面体点阵夹芯结构的单胞参数构造如图2所示,其中Rc为单胞杆的半径,Lc为单胞杆的长度,相邻杆的夹角为120°. 夹芯层的厚度为Hc,杆与基板的角度为θ=arcsin(Hc/Lc). 通过改变Rc、Lc和Hc的大小,实现四面体点阵夹芯结构的参数化构造.
1.2 点阵夹芯结构优化模型与求解
1.2.1 优化模型构造
点阵夹芯结构的优化设计主要体现在单胞的优化设计上,将其结构优化设计模型抽象成式(1)中的数学模型.
(1)
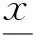
以四面体单胞点阵夹芯结构为例,由于四面体单胞相邻杆的夹角固定,当厚度Hc确定时,圆杆的长度Lc、杆与基板的角度θ也随之唯一确定,因此,设计变量可以从厚度和圆杆半径之中合理选择,目标函数根据实际问题而定.
1.2.2 优化流程及求解方法
在本文的点阵夹芯结构的优化设计中,目标函数与设计变量的关系难以显式表达,为了得到每组设计变量对应的目标函数值,采用有限元软件计算目标函数值,构造问题的二次规划优化模型. 具体分析及优化设计流程如图3所示.
点阵夹芯结构的优化问题属于非线性优化问题. 序列二次规划算法是处理中小规模非线性规划问题最优秀的算法之一,该算法很稳定,对非线性较强的优化问题也具有较高的计算收敛效率. 因此,本文采用序列二次规划算法求解点阵夹芯结构的优化问题.
2 点阵夹芯井字梁结构优化设计
为了验证上面提出的点阵夹芯结构优化模型及算法,以结构刚度最大(最大位移最小)为目标,对四面体夹芯井字梁结构进行优化设计,得到最优的设计方案.
2.1 井字梁及其优化模型构造
2.1.1 点阵夹心井字梁结构
针对这些研究,本文试图探讨大学生词汇知识与词汇应用能力熟练程度的关系,以了解他们所掌握的词汇知识是否能区分不同的熟练程度。
点阵夹芯井字梁结构单梁长230 mm,高40 mm,宽7 mm,几何模型如图4所示. 从夹芯井字梁几何模型示意图可知,由于夹芯井字梁具有对称性,为了减少分析和优化的计算量,取1/4结构进行优化设计.
井字梁结构的夹心层均匀布置正四面体单胞夹芯,1/4井字梁单胞布置如图5所示.
2.1.2 优化模型
优化设计中,以夹芯单胞杆件半径为设计变量,以单胞总体积作为约束条件,整体最大位移最小为优化目标进行优化,优化模型为
(2)
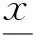
2.2 井字梁有限元分析建模
夹芯井字梁结构整体材料为TC4,其弹性模量为110 GPa,泊松比为0.342. 有限元分析过程中,外部蒙皮采用shell181有限应变壳单元(适用于薄、中等厚度的板壳结构分析,支持线性、大扭转、大应变以及变厚度的非线性分析). 单胞杆件结构采用beam188有限应变梁单元(适合于从细长杆到短粗杆的梁结构分析). 为了使夹芯单胞杆件与蒙皮相连,在蒙皮和单胞杆件相连的地方建立硬点,以便划分单元时在硬点处生成节点,2种单元每个节点都有6个自由度,可以通过共节点的方法进行连接,组成整体有限元模型.
边界条件为:在如图6所示的夹芯井字梁左侧边缘限制X方向的位移自由度和Z方向的转动自由度,前侧边缘限制Z方向的位移自由度和X方向的转动自由度,在右侧和后侧底端限制Y方向的位移自由度;梁中段受到向下的均匀线分布力作用.
通过优化计算,得到了在设计变量约束为0.39 mm≤xi≤1.00 mm、夹芯体积约束为2 717 mm3的参数优化结果. 单胞杆件半径的优化结果如表1所示.
单胞杆半径与位置对应关系如图7所示,其中,黑线的不同粗细代表不同的单胞杆半径,依次为6磅代表半径范围为0.90~1.00 mm;4.5磅代表半径范围为0.70~0.79 mm;3磅代表半径范围为0.60~0.69 mm;2.25磅代表半径范围为0.50~0.59 mm;1.5磅代表半径范围为0.40~0.49 mm;0.75磅代表半径为0.39 mm.
1/4井字梁结构优化过程中算法迭代收敛曲线如图8所示.
从表1和图8可知,设计变量单胞杆件半径都得到了在变量约束范围内适当的半径值,整个寻优过程迭代收敛良好.
将初始设计模型、优化结果模型的1/4模型通过有限元建模生成整体模型,按照2.2节所述边界条件进行分析,结果对比如表2所示.

表1 单胞杆件优化结果
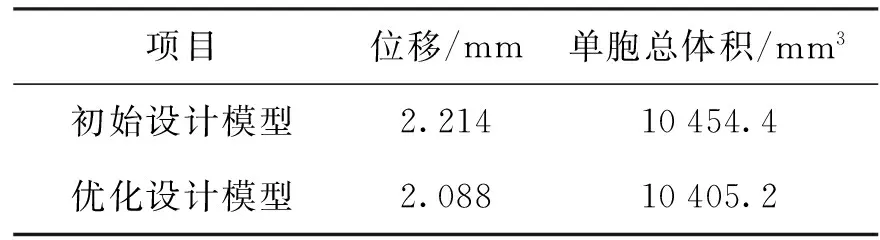
项目位移/mm单胞总体积/mm3初始设计模型2.21410454.4优化设计模型2.08810405.2
从表2可知,在结构总体积基本相等的情况下,经过优化设计得到的模型相对于初始设计模型,刚度提高了5.7%,得到了比较满意的优化结果.
3 结论
1) 通过对四面体单胞夹芯井字梁的优化设计计算,验证了本文所提出的点阵夹芯结构优化模型及优化流程的实用性,优化后的夹芯井字梁刚度有所提高,其单胞布局对工程应用具有一定的参考意义.
2) 通过建立基于ISIGHT的多学科综合优化集成框架,得到了适当的优化结果. 序列二次规划算法对于如点阵结构参数优化的这种多参数、非线性的问题具有较好的收敛性.
[1] EVANS A G, HUTCHINSON J W, FLECK N A, et al. The topological design of multifunctional cellular metals[J]. Progress in Materials Science, 2001, 46(3/4): 309-327.
[2] WICKS N, HUTCHINSON J W. Optimal truss plates[J]. International Journal of Solids & Structures, 2001, 38(38): 5165-5183.
[3] DESHPANDE V S, FLECK N A. Collapse of truss core sandwich beams in 3-point bending[J]. International Journal of Solids & Structures, 2001, 8: 6275-6305.
[4] 曾嵩, 朱荣, 姜炜, 等. 金属点阵材料的研究进展[J]. 材料导报, 2012(5): 18-23. ZENG S, ZHU R, JIANG W, et al. The research progress of metal material structure[J]. Journal of Materials, 2012(5): 18-23. (in Chinese)
[5] KOOISTRA G W, DESHPANDE V S, WADLEY H N G. Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminium[J]. Acta Materialia, 2004, 52(14): 4229-4237.
[6] CHIRAS S, MUMM D R, EVANS A G, et al. The structural performance of near-optimized truss core panels[J]. International Journal of Solids & Structures, 2002, 39(15): 4093-4115.
[7] WICKS N, HUTCHINSON J W. Performance of sandwich plates with truss cores[J]. Mechanics of Materials, 2004, 36(8): 739-751.
[8] CHEN H L, ZHENG Q, WANG P, et al. Dynamic anti-crushing behaviors of woven textile sandwich composites: multilayer and gradient effects[J]. Journal of Composite Materials, 2015, 49(25): 3169-3179.
[9] DAHIWALE N B, PANIGRAHI S K, AKELLA K. Numerical analyses of sandwich panels with triangular core subjected to impact loading[J]. Journal of Sandwich Structures and Materials, 2015, 17(3): 238-257.
[10] 隋允康, 高峰, 龙连春, 等. 基于层次分解方法的桁架结构形状优化[J]. 计算力学学报, 2006, 23(1): 46-51. SUI Y K, GAO F, LONG L C, et al. Shape optimization of truss structures based on hierarchical decomposition method[J]. Journal of Computational Mechanics, 2006, 23(1): 46-51. (in Chinese)
[11] 汪浩, 赵飞, 程远胜, 等. 砰击载荷下金字塔点阵夹层板动力响应分析与估算[J]. 工程力学, 2013(11): 277-285. WANG H, ZHAO F, CHENG Y S, et al. Analysis and estimation of dynamic response of pyramid lattice sandwich plate under the impact load[J]. Engineering mechanics, 2013(11): 277-285. (in Chinese)
[12] 泮世东, 冯吉才, 吴林志. 金字塔点阵夹芯结构的精细优化设计[J]. 哈尔滨工业大学学报, 2011(增刊1): 29-33. PAN S D, FENG J C, WU L Z. Fine optimization design of pyramid lattice sandwich structure[J]. Journal of Harbin Institute of Technology, 2011(Suppl 1): 29-33. (in Chinese)
[13] HYUN S, KARLSSON A M, TORQUATO S, et al. Simulated properties of kagome and tetragonal truss core panels[J]. International Journal of Solids & Structures, 2003, 40(25): 6989-6998.
(责任编辑 吕小红)
Optimization of Lattice Sandwich Structure With Sequential Quadratic Programming Algorithm
LONG Lianchun1, XUE Piao1, LIU Jinpo1, WANG Kunpeng2, TAN Zhi2
(1.College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China; 2.Beijing Institute of Aerospace Systems Engineering, Beijing 100076, China)
To study the influence of the core cell on the structural carrying capacity, in this paper, lattice sandwich structure optimization model was established, which was elaborated by tetrahedron unit cell of sandwich structure. For the purpose of verifying the effectiveness of the optimization model and the solution, a sandwich tic-tac-toe beam structure with the goal of maximizing the stiffness of the structure was optimized by using the method of sequential quadratic programming.
lattice sandwich structure; tetrahedron unit cell; sequential quadratic programming algorithm
2016- 08- 04
国家自然科学基金资助项目(11272020)
龙连春(1963—), 男, 教授, 主要从事复杂系统的分析优化以及超常环境下材料和结构的力学行为方面的研究, E-mail:longlc@bjut.edu.cn
TB 331
A
0254-0037(2016)12-1805-05
10.11936/bjutxb2016080018
