基于独立连续变量和复合指数函数的位移约束平面连续体结构拓扑优化

叶红玲， 尹芳放， 王伟伟， 隋允康

(北京工业大学机械工程与应用电子技术学院， 北京 100124)



基于独立连续变量和复合指数函数的位移约束平面连续体结构拓扑优化

叶红玲， 尹芳放， 王伟伟， 隋允康

(北京工业大学机械工程与应用电子技术学院， 北京 100124)

为了进一步研究连续体结构拓扑优化模型的合理性和可行性，基于独立、连续、映射(independent continuous mapping，ICM)方法，在满足结构位移约束的条件下，通过引入复合指数形式过滤函数对位移约束下质量最小化(minimum weight with a displacement constraint,MWDC)模型进行了改进，建立了基于独立连续变量和复合指数函数的位移约束平面连续体结构拓扑优化模型，并进行了优化求解. 同时，利用M语言，基于Matlab软件平台，开发了相应的拓扑优化计算程序，并针对4种典型平面连续体结构进行了数值验证，分别比较分析了体积约束下的柔顺度最小化(minimum compliance with a volume constraint,MCVC)模型、MWDC模型以及改进的MWDC模型所得到的最优拓扑结构. 数值结果表明：采用复合指数形式过滤函数改进的MWDC优化模型迭代次数更少，优化求解计算效率更高.

平面连续体结构；拓扑优化；独立、连续、映射(ICM)方法；位移约束；复合指数函数

根据结构设计变量范围的不同，结构优化问题可以分为尺寸优化、形状优化和拓扑优化3个层次. 结构拓扑优化相对于尺寸优化与形状优化具有更多的设计自由度，从而获得了更大的设计空间. 此外，拓扑优化在节省材料方面比尺寸优化和形状优化更为显著，因而可以取得更大的经济效益. 且拓扑优化待确定的参数较多，求解难度较大，因此更具有发展前景和挑战性.

连续体结构拓扑优化设计是指在设计区域中搜索出一个优化子集，在满足预设约束条件(如应力约束、应变约束或频率约束等)的基础上，寻求使目标函数取得极小值时材料在平面或空间内的最优分布及结构的最佳传力路径的一类优化问题. 目前，连续体结构拓扑优化中已经建立了多种较为完善的拓扑表达形式与材料插值模型方法[1]，其中经典方法包括：均匀化方法[2](homogenization method)、相对密度法[3](relative denisity method)、水平集方法[4](level set method)、渐进结构优化法[5](evolutionary structural optimization method)、双向渐进优化法[6](bidirectional evolutionary structural optimization method)、相场法[7](phase field method)、节点变量法[8]、独立连续映射法[9](independent continuous mapping method,ICM)等.

根据连续体结构拓扑优化问题中所包含的“三要素”即目标函数、设计变量和约束条件中的目标函数的属性，可以将其划分为不同的连续体结构拓扑优化模型. Yi等[10]按照结构的物理量将连续体拓扑优化问题划分为结构经济指标和结构性能指标两大类. 其中，结构经济指标是指结构的体积、质量或造价等；结构性能指标是指结构的力学性能，如结构柔顺度、位移、应力、固有频率、振幅等. 由此结构拓扑优化模型可以分为体积约束下的柔顺度最小化(minimum compliance with a volume constraint，MCVC)的结构性能指标模型和位移约束下质量最小化(minimum weight with a displacement constraint，MWDC)的结构经济指标模型. 模型不同，将导致其适用性和合理性也不尽相同，彭细荣等[11]针对包括MCVC模型和MWDC模型的连续体结构拓扑优化合理模型进行了一步探讨.

本文基于ICM拓扑优化方法，针对MCVC模型和MWDC模型进一步深入研究，并引入新的过滤函数，即复合指数过滤函数对MWDC拓扑优化模型进行了改进. 采用单位虚载荷法将结构目标点位移显式化处理，并利用拉格朗日乘子法，推导出了采用新过滤函数的连续体结构MWDC模型的求解算法. 同时，基于MATLAB软件平台开发并编译了136行平面连续体结构拓扑优化程序，并利用该程序，通过4个数值算例对改进的模型进行了结果验证与比较.

1 基于ICM方法的MWDC模型概述

ICM拓扑优化方法[12-13]，是以一种以独立于单元具体物理参数的变量来表征单元“有”与“无”的拓扑优化模型. 在优化过程中，利用过滤函数将本质上属于0/1的离散拓扑变量映射为[0，1]的连续变量，使得单元上的物理量同拓扑变量之间的关系由不确定、不连续、不可导变成确定、连续、可导，从而将离散拓扑优化问题转化成了光滑的数学模型. 优化迭代结束后，再通过逆映射将连续的变量反演为离散变量. ICM结构拓扑优化方法通常以结构整体质量最小(或结构整体体积最小)为优化目标，以结构响应作为约束条件，是一种典型的MWDC结构经济指标模型. 其以位移为约束的结构整体质量最小的拓扑优化模型可以表示为

(1)

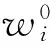
典型的MCVC优化模型是基于固体各向同性材材惩罚(solid isotropic microstructured with penalization，SIMP)方法[14-15]的拓扑优化模型，其表达式为

(2)

式中：c(x)为结构的柔顺度；x为设计变量；U为位移列向量；K为整体刚度矩阵；xe为单元设计变量；ue为单元位移列向量；k0为单元刚度矩阵；V(x)为设计变量对应状态下的结构体积；V0为初始结构体积；f为体积比；F为载荷列向量；xmin与xmax分别为单元内设计变量的下限值与上限值；p为惩罚因子.

由于工程中最常用的结构物理量指标为结构质量(或体积)、强度、刚度及稳定性等，因此相比于MCVC模型，MWDC模型更符合工程问题的惯常提法. 在MWDC模型的发展中，为了便于与由Sigmund[15]所提出的典型的MCVC优化模型所得最优拓扑结构进行分析比较，Yi等[10]针对幂函数形式过滤函数的MWDC结构经济指标模型进行了研究.

在ICM优化方法中，过滤函数发挥着极其重要的作用. 过滤函数不仅可以实现对于拓扑变量的过滤和筛选，完成对拓扑变量由连续模型向离散模型的回归，而且过滤函数在建模中还起到了识别几何或物理量的作用，比如

(3)

(4)

综上所述，可以得到引入过滤函数的位移约束下结构质量最小的连续体结构拓扑优化MWDC模型表达式为

(5)

式中：fw(ti)和fk(ti)为过滤函数.

在连续体结构拓扑优化问题中，选取不同形式的过滤函数，直接会导致优化求解计算效率与优化结果的差异. ICM方法中所采用的过滤函数主要包括幂函数形式的过滤函数和复合指数函数形式的过滤函数等[13]，其数学表达式分别为

式中α、γ为常数，可以通过数值试验的方法获得.

由文献[16]可知，对于幂函数形式的过滤函数和复合指数形式的过滤函数2种常见过滤函数而言，在设计变量[0,1]区间中，采用复合指数形式的过滤函数相比于幂函数形式的过滤函数更易使对应设计变量迅速趋近于1. 本文将研究采用

(6)

(7)

所示的复合指数函数形式过滤函数对式(1)中单元质量与单元刚度矩阵进行过滤，从而进一步探讨过滤函数对MWDC模型拓扑优化结果的影响.

2 改进的MWDC结构性能指标优化模型建立与求解

2.1 位移约束下改进的MWDC优化模型中的位移约束显式化

由莫尔定理可知，结构任意节点在某一方向上的广义位移可表示为

(8)式中：si为第i个单元对于结构目标点位移的影响值；σig为设计区域结构中实载荷下的单元应力向量；εiv为设计区域结构中虚载荷下的单元应变向量.

根据虚功原理“外力在虚位移上做的功等于内力在虚位移导致的虚变形上所做的虚功”，可以得到

(9)

(10)

根据有限元原理，设计域结构的单元刚度

(11)

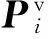
引入复合指数型过滤函数，则单元刚度矩阵可以表示为

(12)

将设计域结构的单元刚度代入虚功原理公式(10)，可以得到设计区域中目标点位移为

(13)

将得到的单元刚度矩阵代入设计区域中目标点位移公式，可以得到目标点位移的显式化表达式为

(14)

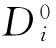
通过上述转化，借助刚度矩阵过滤函数，位移约束由设计变量的隐函数转化为了显函数.

2.2 位移约束下改进的MWDC优化模型求解

将上述得到的目标点位移的显式化表达式(14)代入如式(1)所示的MWDC结构性能指标位移约束下结构整体质量最小的优化模型，可以得到改进的MWDC结构性能指标拓扑优化模型为

(15)

为了获得上述优化模型的设计变量最优解，利用拉格朗日乘子法进行计算分析. 引入拉格朗日乘子λ，得到拉格朗日方程为

(16)

拉格朗日函数的一阶导数可以表示为

(17)

(18)

消去拉格朗日乘子λ可得最终解为

(19)

至此，完成了该改进的MWDC结构性能指标拓扑优化模型设计变量的分析求解.

2.3 改进的MWDC优化模型优化收敛准则与计算流程

(20)

基于以上位移约束下改进的MWDC优化模型，将整个求解过程利用M语言在Matlab软件平台进行了编译与实现，其结构拓扑优化程序流程如图1所示.

3 数值算例

为了进一步验证该改进的MWDC优化模型的有效性与可行性，本文给出4个经典数值算例，分别对采用幂函数形式过滤函数的MCVC模型、传统的MWDC模型与采用复合指数形式过滤函数的改进的MWDC模型所得到的最优拓扑结构进行分析比较.

算例1左端固支悬臂梁，其结构如图2所示. 基结构为32 mm×20 mm×1 mm，载荷为F=1 N，弹性模量E0=1.0 MPa，泊松比为μ=0.3.

采用MCVC模型、传统的MWDC模型以及本文改进的MWDC模型的3种优化模型所得到的平面连续体最优拓扑结构及迭代次数分别如表1所示，与该结构相对应的拓扑优化结构质量迭代曲线以及结构位移迭代过程曲线如图3、4所示.

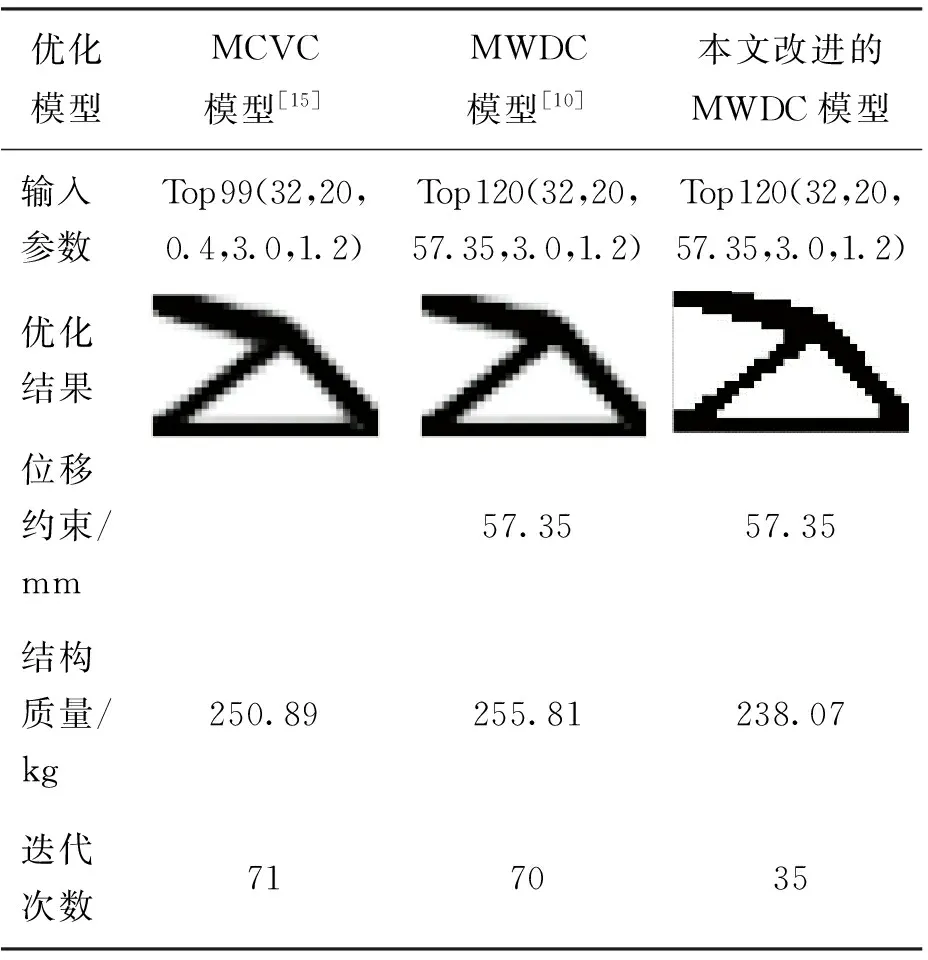
表1 左端固支悬臂梁平面连续体结构拓扑优化结果

根据以上优化结果，采用MCVC模型、传统的MWDC模型以及改进的MWDC模型3种优化模型所得到的最优拓扑结构基本相同. 其中，采用MCVC模型与传统的MWDC模型所得到的优化后结构总质量差别较小，而采用改进的MWDC模型所得到的优化后结构总质量较MCVC模型与传统的MWDC模型分别降低5.11%和6.93%. 此外，采用3种模型进行拓扑优化求解的迭代次数分别为71、70、35次. 可见，采用改进后的MWDC模型较MCVC模型与传统的MWDC模型在优化求解效率上分别实现了50.70%和50.00%的显著提升.

算例2左端固支带孔悬臂梁，其结构如图5所示. 结构为45 mm×30 mm×1 mm，载荷为F=1 N，弹性模量E0=1.0 MPa，泊松比为μ=0.3，孔的位置为从左往右横向长度的1/3和纵向长度的1/2，半径为纵向长度的1/3.

采用MCVC模型、传统的MWDC模型以及本文改进的MWDC模型的3种优化模型所得到的平面连续体最优拓扑结构及迭代次数分别如表2所示，与该结构相对应的拓扑优化结构质量迭代曲线以及结构位移迭代过程曲线如图6、7所示.

表2 左端固支带孔悬臂梁平面连续体结构拓扑优化结果

根据以上优化结果可知，采用MCVC模型、传统的MWDC模型以及改进的MWDC模型3种优化模型所得到的最优拓扑结构基本相同. 其中，采用改进的MWDC模型所得到的优化后结构总质量较MCVC模型与传统的MWDC模型分别降低了2.08%和7.90%. 此外，采用3种优化模型进行拓扑优化求解的迭代次数分别为34、51、11次. 可见，采用改进的MWDC模型较MCVC模型与传统的MWDC模型在优化求解效率方面具有显著提升.

算例3左端固支右端中部加载悬臂梁，其结构如图8所示. 基结构为80 mm×50 mm×1 mm，载荷为F=9 kN，弹性模量E0=1.0 MPa，泊松比为μ=0.3.

采用MCVC模型、传统的MWDC模型以及本文改进的MWDC模型的3种优化模型所得到的平面连续体最优拓扑结构及迭代次数分别如表3所示，与该结构相对应的拓扑优化结构质量迭代曲线以及结构位移迭代过程曲线如图9、10所示. 由表3可见，采用改进的MWDC模型迭代次数最少，结构质量最轻，由表3可见.

表3 左端固支右端中部加载悬臂梁平面连续体结构拓扑优化结果

Table 3 Plane continuum structure topology optimization results for cantilever beam with a load at the middle of right eadge

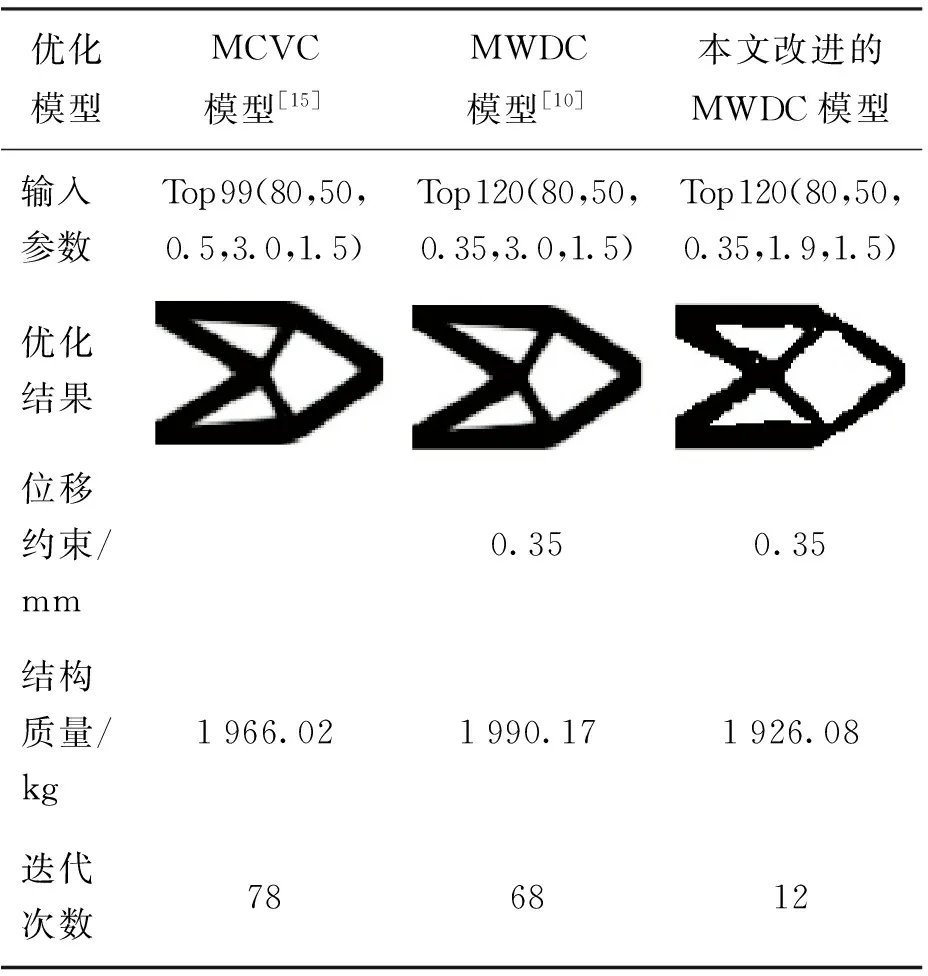
优化模型MCVC模型[15]MWDC模型[10]本文改进的MWDC模型输入参数Top99(80,50,0.5,3.0,1.5)Top120(80,50,0.35,3.0,1.5)Top120(80,50,0.35,1.9,1.5)优化结果位移约束/mm0.350.35结构质量/kg1966.021990.171926.08迭代次数786812

算例4 MBB简支梁的一半，其结构如图11所示. 基结构为60 mm×20 mm×1 mm，载荷为F=1 N，弹性模量E0=1.0 MPa，泊松比为μ=0.3.

采用MCVC模型、MWDC模型以及改进的MWDC模型的3种优化模型所得到的平面连续体最优拓扑结构及迭代次数分别如表4所示，与该结构相对应的拓扑优化结构质量迭代曲线如图12所示. 可以看到采用改进的MWDC模型较MCVC模型与传统的MWDC模型在优化求解效率方面具有显著提升，迭代次数最少.

表4 MBB平面梁连续体结构拓扑优化及迭代次数

Table 4 Plane continuum structure topology optimization for MBB beam and the number of iterations

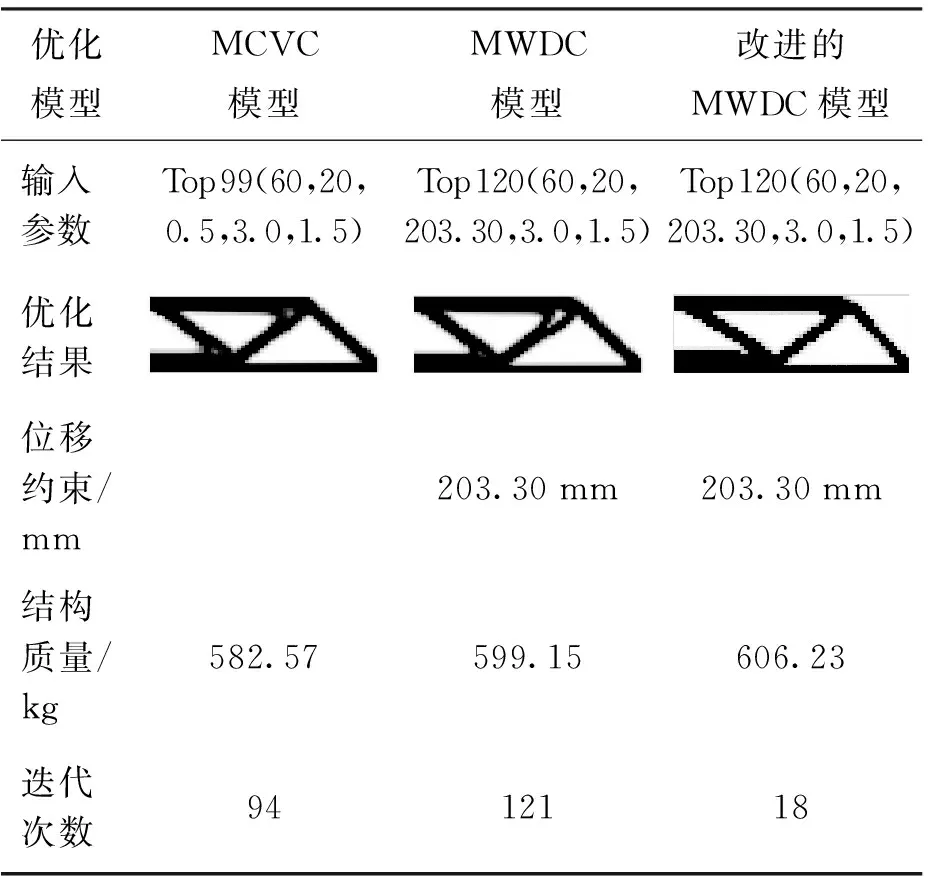
优化模型MCVC模型MWDC模型改进的MWDC模型输入参数Top99(60,20,0.5,3.0,1.5)Top120(60,20,203.30,3.0,1.5)Top120(60,20,203.30,3.0,1.5)优化结果位移约束/mm203.30mm203.30mm结构质量/kg582.57599.15606.23迭代次数9412118

4 结论

1) 采用改进的MWDC结构经济指标模型所得到的最优拓扑结构与采用MCVC结构性能指标模型和传统的MWDC结构经济指标模型所得到的最优拓扑结构基本相同. 因此，改进的MWDC结构经济指标模型能够满足解决以目标点位移作为约束条件的拓扑优化问题.

2) 采用改进的MWDC结构经济指标模型所得到的优化后结构的总质量较采用MCVC结构性能指标模型和传统的MWDC结构经济指标模型均有所降低.

3) 在拓扑优化求解收敛速率方面，采用改进的MWDC结构经济指标模型较采用MCVC结构性能指标模型和传统的MWDC结构经济指标模型均实现了显著提升，大幅降低了结构拓扑优化问题的求解成本.

[1] 罗震, 陈立平, 黄玉盈, 等. 连续体结构的拓扑优化设计[J]. 力学进展, 2004, 34(4): 463-476. LUO Z, CHEN L P, HUANG Y Y, et al. Topological optimization design for continuum structures[J]. Advances in Mechanics, 2004, 34(4): 463-476. (in Chinese)

[2] BENDSØE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics & Engineering, 1988, 71(2): 197-224.

[3] MLEJNEK H P, SCHIRRMACHER R. An engineer’s approach to optimal material distribution and shape finding[J]. Computer Methods in Applied Mechanics & Engineering, 1993, 106(1/2): 1-26.

[4] MAKHIJA D, MAUTE K. Numerical instabilities in level set topology optimization with the extended finite element method[J]. Structural & Multidisciplinary Optimization, 2014, 49(2): 185-197.

[5] WANG B Q, WANG B L, HUANG Z Y. Topology optimization for constrained layer damping plates using evolutionary structural optimization method[J]. Advanced Materials Research, 2014, 894: 158-162.

[6] 匡兵, 李应弟, 刘夫云, 等. 基于单元密度进化步长控制的双向渐进结构优化方法[J]. 计算力学学报, 2016(1): 15-21. KUANG B, LI Y D, LIU F Y, et al. Bi-directional evolutionary structural optimization method based on control for evolutionary step length of element density[J]. Chinese Journal of Computational Mechanics, 2016(1): 15-21. (in Chinese)

[7] TAKEZAWA A, NISHIWAKI S, KITAMURA M. Shape and topology optimization based on the phase field method and sensitivity analysis[J]. Journal of Computational Physics, 2010, 229(7): 2697-2718.

[8] 占金青, 杨康, 黄志超. 基于节点变量法的连续体结构拓扑优化设计[J]. 农业机械学报, 2014, 45(9): 329-332. ZHAN J Q, YANG K, HUANG Z C. Topology optimization of continuum structures using node variable method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 329-332. (in Chinese)

[9] 隋允康. 建模变换优化——结构综合方法新进展[M]. 大连: 大连理工大学出版社, 1996: 2-65.

[10] YI G L, SUI Y K. An adaptive approach to adjust constraint bounds and its application in structural topology optimization[J]. Journal of Optimization Theory & Applications, 2016, 169(2): 656-670.

[11] 彭细荣, 隋允康. 对连续体结构拓扑优化合理模型的再探讨[J]. 固体力学学报, 2016(2): 181-191. PENG X R, SUI Y K. A further discussion on rational topology optimization models for continuum structures[J]. Chinese Journal of Solid Mechanics, 2016(2): 181-191. (in Chinese)

[12] SUI Y, YANG D. New method for structural topological optimization based on the concept of independent continuous variables and smooth model[J]. Acta Mechanica Sinica, 1998, 14 (2): 179-185.

[13] 隋允康, 叶红玲. 连续体结构拓扑优化的ICM方法[M]. 北京: 科学出版社, 2014: 27-59.

[14] BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635-654.

[15] SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization, 2001, 21 (2): 120-127.

[16] 叶红玲, 沈静娴, 隋允康. 频率约束的三维连续体结构动力拓扑优化设计[J]. 力学学报, 2012, 44(6): 1037-1045. YE H L, SHEN J X, SUI Y K. Dynamic topological optimal design of three-dimensional continuum structures with frequencies constraints[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 1037-1045. (in Chinese)

(责任编辑 吕小红)

Planar Continuum Structure Topology Optimization With Displacement Constraint Based on Independent Continuous Variables and Composite Exponential Function

YE Hongling, YIN Fangfang, WANG Weiwei, SUI Yunkang

(College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China)

To study the rationality and feasibility of the continuum structure topology optimization model， an improved minimum weight with a displacement constraint (MWDC) model by using exponential function was studied, which was based on the independent continuous mapping (ICM) method. A new topology optimization model for the problem of planar continuum structure with independent continuous variables and displacement constraints was established and solved. At the same time, a calculator program was developed and compiled based on the MATLAB in accordance with the new method. In addition, four typical numerical examples were adopted to verify the presented method. The topological results by taking advantage of MCVC model, MWDC model and improved MWDC model were compared with the view of structural mass and iterative numbers.Numerical results show that there is obvious advantage to solve the problem of planar continuum structure topology optimization with the improved MWDC optimization model in terms of calculation efficiency.

planar continuum structure; topology optimization; independent continuous mapping (ICM) method; displacement constraint；composite exponential function

2016- 08- 01

国家自然科学基金资助项目(11072009)；北京市教育委员会资助项目(KM201610005001);北京工业大学基础研究基金(001000514313003)

叶红玲(1972—)， 女， 副教授， 主要从事结构优化与多学科结构分析方面的研究， E-mail: yehongl@bjut.edu.cn

TP 31；O 34

A

0254-0037(2016)12-1810-08

10.11936/bjutxb2016080005