不确定车轨耦合系统运行舒适度分析

项 盼， 赵 岩， 林家浩

(1.中车大连机车车辆有限公司， 大连 116022；2.大连理工大学运载工程与力学学部，工业装备与结构分析国家重点实验室， 大连 116023)



不确定车轨耦合系统运行舒适度分析

项 盼1,2， 赵 岩2， 林家浩2

(1.中车大连机车车辆有限公司， 大连 116022；2.大连理工大学运载工程与力学学部，工业装备与结构分析国家重点实验室， 大连 116023)

运行舒适度是车辆动力性能的重要指标，对其精准高效的预估能够提高车辆设计水平、降低研发成本. 综合考虑动力学分析中的不确定因素，分别以随机变量和随机过程描述系统参数和荷载激励，基于虚拟激励法和改进摄动法，提出了复合随机振动问题的确定性分析方法. 算例中，考虑9个随机变量参数，计算车体不同位置在轨道不平顺激励下的舒适度指标. 结果表明：该方法能够很好地与Monte Carlo模拟吻合，验证了本文方法的正确性，并指出忽略参数不确定性会给出过高的舒适度评价.

车轨耦合系统；运行舒适度；随机振动；虚拟激励法；改进摄动法

不确定性是自然界的本质属性，更普遍存在于工程结构的设计与分析中. 在铁路车辆动力响应分析中，不确定性来源于2个方面：一是系统本身，由于制造装配误差等原因，车辆自身参数存在一定的不确定性. Mazzola等[1]采用统计方法分析二系抗偏器参数不确定性对临界速度设计的影响，结合Monte Carlo和试验设计理论，假设刚度和阻尼系数均服从独立高斯分布，建立临界速度关于刚度和阻尼系数的二阶代理模型. Suarez等[2]通过灵敏度分析研究车辆惯性参数对车辆动力性能的影响，逐一评价安全性、轨道疲劳和运行舒适度3类指标对12个惯性参数在不同工况下的灵敏度，对比模拟结果，指出质量和绕垂向转动惯量对动力性能影响最大. Mastinu等[3]推导了两自由度模型响应标准差关于悬挂参数的解析表达式，并在此基础上进行参数灵敏度分析及多目标优化. 另一方面，轨道不平顺作为公认的车辆振动主激励源，也具有显著的随机特性. Yau等[4]采用确定的不平顺函数作为激励，研究列车高速通过简支桥和三跨连续桥时的振动，并指出轨道不平顺对簧上质量的垂向加速度响应影响显著，进而影响运行舒适度的评价. Lei等[5]将轨道垂向不平顺视为各态历经的平稳高斯随机过程，通过三角级数法进行模拟. Zhao等[6]应用直接积分法和离散快速傅里叶变换研究磁悬浮列车- 导轨系统的随机响应，并进行了车辆舒适度评价. Zhang等[7-8]基于虚拟激励法和辛数学方法，建立了复杂车轨耦合系统随机振动算法，并提出了以运行舒适度为目标的优化方法. 然而，同时考虑车辆参数随机性和轨道随机不平顺激励的复合随机振动分析并不多见，面临着物理描述与计算方法上的双重困难. 本文基于虚拟激励法，根据轨道不平顺功率谱密度及激励方式构造虚拟激励计算车辆加速度响应功率谱，建立基于Sperling指标的快速算法，该方法不需要积分运算，格式简单效率高；同时以随机变量描述车辆参数的不确定性，在参数小变异前提下，采用Wu等[9]提出的改进摄动算法，该方法避免了递推方程的推导和灵敏度矩阵的计算，具有精确高效的特点.

1 基于虚拟激励法的舒适度分析

虚拟激励法是一种精确高效的随机振动算法，已得到工程界广泛的认可[10-12]. 将其运用于轨道不平顺激励下的车辆动力学分析，可以方便地求出车体位移、加速度等响应功率谱，进而建立车辆运行舒适度的快速评估方法.

1.1 虚拟激励法

线性系统的运动方程为

(1)

式中：m、c、k分别为质量、阻尼、刚度矩阵；p(t)为平稳随机过程.

根据传统随机振动理论，响应的功率谱密度矩阵为

Sx(iω)=H(iω)*Sp(iω)H(iω)T

(2)

式中：H(iω)=[(k-ω2m)+iωc]-1为系统的频响矩阵；Sp为p(t)的功率谱密度矩阵；上标“*”表示复共轭运算；上标“T ”表示转置运算.

构造简谐虚拟激励

(3)

须满足

(4)

求得频域上虚拟响应为

(5)

则相应的功率谱可以表示为

(6)

虚拟激励法将平稳随机振动分析转化为简谐振动分析，给出响应功率谱的统一求解形式.

1.2 舒适度评估方法

假设轨道不平顺r(x)为随里程变化的零均值高斯随机过程，功率谱密度为Sr(Ω)，Ω为空间圆频率，rad/m. 当列车在轨道上以速度v匀速行驶时，可将空间随机过程转化为时域上的平稳随机过程r(t)，其功率谱密度为

Sr(ω)=Sr(Ω)/v，Sr(f)=2πSr(ω)

(7)

式中：ω为时间圆频率，rad/s；f=ω/2π为时间频率，Hz.

以四轮对车辆为研究对象，各轮对先后受到相同的轨道不平顺激励，激励是完全相干的，因此构造虚拟激励

(8)

式中ti(i=1,2,3,4)是相对第1轮对的时滞，故t1=0. 虚拟不平顺激励式(8)通过轮轨关系作用于车轨耦合系统，求解这一激励下的虚拟加速度响应，根据式(6)即可求得加速度响应功率谱Sa(f).

车辆的振动为随机振动，其上、下截止频率分别fu和fl，采样频率为

(9)

式中N为采样数目，Δf=(fu-fl)/N.

根据三角级数模拟，频率成分fk的振动加速度幅值为

(10)

根据Sperling公式，计算各频率下的舒适度指标

(11)

计算频率范围内总的舒适度指标为

(12)

由以上推导可见，基于虚拟激励法的舒适度评估方法避免了积分运算和随机样本的模拟，仅在离散的频点进行谐响应分析，是舒适度分析的高效算法.

2 改进摄动法

摄动法是处理随机参数问题的有效手段，在参数变异较小的前提下，摄动法具有精度高、计算量小的特点. 本文从舒适度指标的泰勒展式出发，构造确定性算法，避免递推方程推导和灵敏度矩阵的计算.

2.1 二阶摄动

将舒适度指标W关于随机参数ξ在零均值处二阶展开

(13)

式中：

W0=W(ξ)|ξ=0

根据式(13)求响应W(ξ)的均值和协方差

(14)

cov[W(ξ),W(ξ)]=

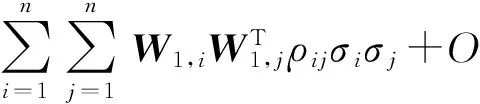
(15)

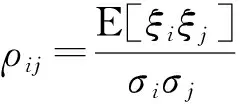
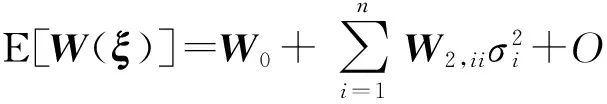
(16)

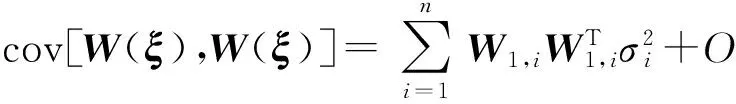
(17)

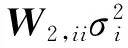
将标准差σs视为小量，构造确定性向量as

(18)

将as和-as分别代入式(13)

(19)

由式(19)可得

(20)

记

zs=W(as)+W(-as)-2W0

ws=Ws(as)-Ws(-as)

(21)

将式(20)代入式(16)和(17)

(22)

(23)

2.2 高阶摄动

若随机变量不仅互不相关，而且概率密度函数对称，可考虑更高的精度

(24)

(25)

由式(25)得

(26)

记

zs=W(bs)+W(-bs)-2W0

ws=W(bs)-W(-bs)

(27)

由式(26)，均值和协方差分别为

(28)

cov [W(ξ),W(ξ)]=

(29)

由式(28)(29)给出的均值和协方差估计具有3阶精度.

3 算例

如图1所示，车辆采用10自由度刚体模型，轨道假设为无限长周期结构，采用线性赫兹弹簧建立轮轨耦合关系[13]. 轨道不平顺以波长1 m为界，分别采用美国6级谱和中国短波不平顺谱[14]. 考虑车身质量和转动惯量、二系悬挂刚度和阻尼、转向架质量和转动惯量、一系悬挂刚度和阻尼、轮对质量等9个参数为随机变量，随机向量α={Mc,Jc,kc,cc,Mt,Jt,kt,ct,Mw}，其分量表示为

αs=μs(1+γsξs)，s=1,2,…,9

(30)

式中：ξs为无量纲零均值随机变量；μs和γs为确定性常数.

αs的均值和方差计算如下

E[αs]=E[μs(1+γsξs)]=μs

(31)

D[αs]=E[(αs-μs)2]=

(32)

可见，μs为随机变量αs的均值，γs≪1，表示随机扰动偏离均值的程度.

根据车辆参数的特征采用Wigner分布，则随机变量的概率密度函数为

(33)

车辆运行时速为180 km/h，γ分别取0.05和0.10，计算图1中5个位置的舒适度指标的均值和标准差，并与10 000样本Monte Carlo模拟结果进行比较，如表1所示. 其中，舒适度指标均值最大相对误差不超过0.05%，标准差最大相对误差不超过3%，可见本文方法与Monte Carlo模拟能够很好地吻合，验证了本文方法的有效性. 更多的计算表明随机参数变异的增大会导致平稳性指标总体均值和标准差的增加，也就是说忽略参数不确定性会高估车辆运行的舒适度.

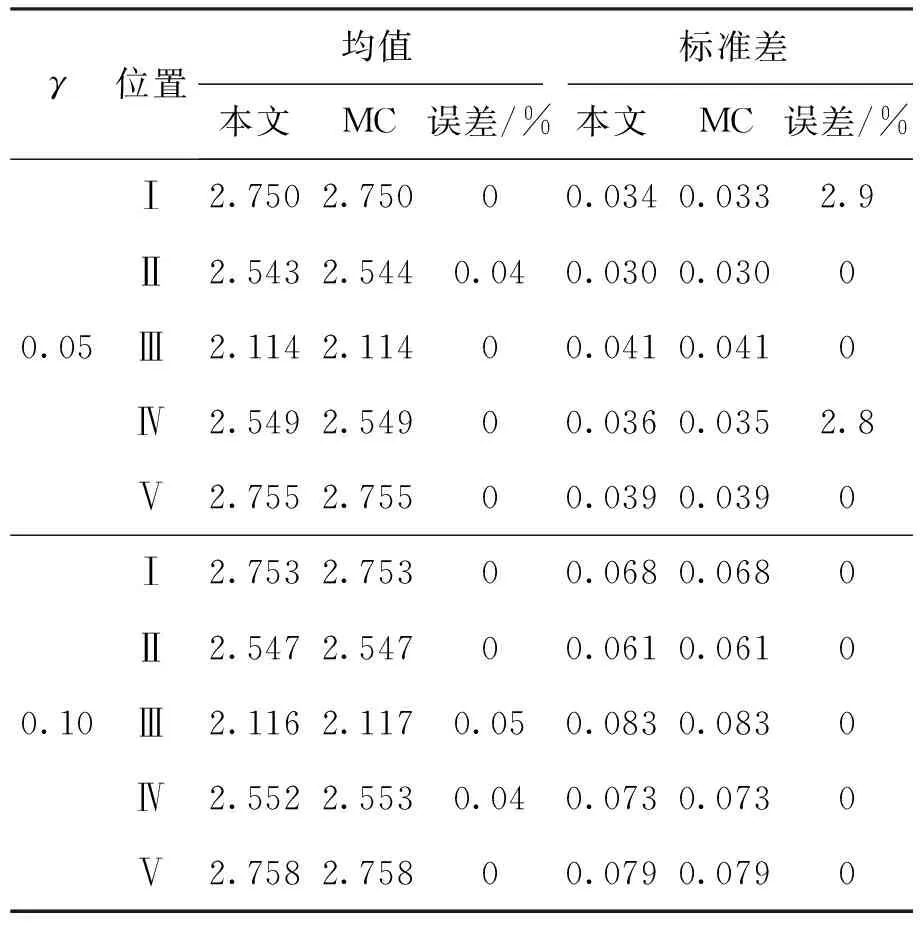
表1 γ不同取值舒适度指标均值与标准差

考虑参数不确定性的传播，计算舒适度指标的变异系数如图2所示. 舒适度指标的变异系数随着γ增大线性增加，其斜率小于1，说明参数不确定性的传播没有被放大. 注意到由于车辆模型前后对称，舒适度指标的变异特性也呈现前后对称的特点，因此仅计算位置Ⅰ、Ⅱ、Ⅲ的舒适度指标.

车速是影响舒适度指标的重要因素，计算不同车速下舒适度指标的变异系数，如图3所示. 位置Ⅰ和Ⅱ处，随车速的提高，参数不确定性的传播被放大了，而位置Ⅲ处则正好相反，在车速较高的情况下，对应相同的γ，舒适度指标变异系数反而较小. 车体采用两自由度刚体模型，振型分别为垂向平动和绕质心转动2种模式，平动对应特征频率较低，转动对应特征频率较高，随着车速提高，绕质心转动对垂向振动的加成更显著，位置Ⅰ和Ⅱ处的舒适度指标的均值，标准差和变异系数都增加. 位置Ⅲ即质心位置的垂向运动不受转动的影响，舒适度指标的标准差不随车速提高而增大，但均值随车速的提高而增大，因此变异系数反而减小.

4 结论

1) 提出了不确定车轨耦合系统运行舒适度的确定性算法，算法的优点在于2个方面：基于虚拟激励法的舒适度评估方法，避免了积分运算和随机样本的模拟，仅在离散的频点进行谐响应分析，计算简单高效；摄动快速算法避免了递推方程的推导和随机矩阵求导运算.

2) 采用确定性分析手段解决了复合随机问题，数值结果与Monte Carlo模拟吻合，证明了本文方法的有效性.

3) 忽略参数不确定性会导致过高地估计车辆运行舒适度，同时参数不确定性的传播受响应自由度的影响，因此在进行车辆运行舒适度分析时有必要考虑参数的不确定性.

[1] MAZZOLA L, BRUNI S. Effect of suspension parameter uncertainty on the dynamic behaviour of railway vehicles[J]. Applied Mechanics and Materials, 2012, 104: 177-185.

[2] SUAREZ B, FELEZ J, MAROTO J, et al. Sensitivity analysis to assess the influence of the inertial properties of railway vehicle bodies on the vehicle’s dynamic behaviour[J]. Vehicle System Dynamics, 2013, 51(2): 251-279.

[3] MASTINU G, GOBBI M, PACE G D. Analytical formulae for the design of a railway vehicle suspension system[J]. Journal of Mechanical Engineering Science, 2001, 215(6): 683-698.

[4] YAU J, YANG Y, KUO S. Impact response of high speed rail bridges and riding comfort of rail cars[J]. Engineering Structures, 1999, 21(9): 836-844.

[5] LEI X, NODA N A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile[J]. Journal of Sound and Vibration, 2002, 258(1): 147-165.

[6] ZHAO C F, ZHAI W M. Maglev vehicle/guideway vertical random response and ride quality[J]. Vehicle System Dynamics, 2002, 38(3): 185-210.

[7] ZHANG Y W, LIN J H, ZHAO Y, et al. Symplectic random vibration analysis of a vehicle moving on an infinitely long periodic track[J]. Journal of Sound and Vibration, 2010, 329(21): 4440-4454.

[8] ZHANG Y W, ZHAO Y, ZHANG Y H, et al. Riding comfort optimization of railway trains based on pseudo-excitation method and symplectic method[J]. Journal of Sound and Vibration, 2013, 332(21): 5255-5270.

[9] WU F, GAO Q, XU X, et al. A modified computaional scheme for the stochasitcpertubation finite element method[J]. Latin American Journal of Solids and Structures, 2015, 12(13): 2480-2505.

[10] LIN J H. A fast CQC algorithm of PSD matrices for random seismic responses[J]. Computers & Structures, 1992, 44(3): 683-687.

[11] LIN J H, ZHANG W S, LI J J. Structural responses to arbitrarily coherent stationary random excitations[J]. Computers & Structures, 1994, 50(5): 629-633.

[12] LIN J, ZHAO Y, ZHANG Y. Accurate and highly efficient algorithms for structural stationary/non-stationary random responses[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 191(1/2): 103-111.

[13] LU F, KENNEDY D, WILLIAMS F W, et al. Symplectic analysis of vertical random vibration for coupled vehicle-track systems[J]. Journal of Sound and Vibration, 2008, 317(1): 236-249.

[14] XIANG P, ZHAO Y, LIN J H, et al. Random vibration analysis for coupled vehicle-track systems with uncertain parameters[J]. Engineering Computations, 2016(2): 443-464.

(责任编辑 杨开英)

Riding Comfort Analysis for Coupled Vehicle-track Systems With Uncertain Parameters

XIANG Pan1, ZHAO Yan2， LIN Jiahao2

(1.CRRC Dalian Co., Ltd., Dalian 116022, China；2. State Key Laboratory of Structural Analysis for Industrial Equipment, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116023, China)

Riding comfort is an important index of the vehicle dynamic performance, of which the accurate and efficient prediction is of great importance for improving the vehicle design and reducing the costs. In this paper, the dynamic analysis with uncertain factors was studied. The uncertain parameters were described by random variables and the random excitations were described by random processes, respectively. Based on the pseudo-excitation method combined with the improved perturbation method, a deterministic approach was established for the analysis of double random vibration problems. In the numerical example, nine random variable parameters were considered and the riding comfort indexes at different positions under track irregularities were investigated. Results show that this method agrees well with those by using Monte Carlo method, and ignoring parameter uncertainty will lead to higher comfort evaluation.

coupled vehicle-track systems; riding comfort; random vibration; pseudo-excitation method; improved perturbation method

2016- 08- 16

国家“973”计划资助项目(2015CB057804)

项 盼(1985—)， 男， 博士研究生， 主要从事车辆动力学方面的研究， E-mail:p_xiang@foxmail.com

林家浩(1941—)， 男， 教授， 博士生导师， 主要从事随机振动方面的研究， E-mail：jhlin@dlut.edu.cn

U 260

A

0254-0037(2016)12-1781-06

10.11936/bjutxb2016080037