组合结构的残余振动最小化结构优化设计

阎 琨, 刘晓德, 程耿东

(1.大连理工大学工业装备结构分析国家重点实验室, 大连 116023；2.北京大学力学与工程科学系， 北京 100871)



组合结构的残余振动最小化结构优化设计

阎 琨1, 刘晓德2, 程耿东1

(1.大连理工大学工业装备结构分析国家重点实验室, 大连 116023；2.北京大学力学与工程科学系， 北京 100871)

为了解决残余振动直接影响结构性能的问题，研究了最小化残余振动为目标的组合结构优化设计，目标函数为能够总体衡量结构残余振动响应的二次型积分形式的性能指标，设计变量为组合结构参数化描述时采用的形状尺寸等参数. 采用半解析法灵敏度分析克服了将这一方法应用于包含多种单元、多种类型设计变量的组合结构优化的困难，实现了采用Matlab将Ansys作为黑箱调用进行结构优化设计. 数值算例展示了该方法的有效性.

残余振动；半解析灵敏度求解方法；组合结构；结构优化

结构在工作中，由于各种原因会受到外力作用. 外力作用结束后，结构往往不会立刻恢复至静止状态，而是会发生自由振动，称为结构的残余振动. 残余振动对精密系统的影响十分显著. 为使结构在被激振后尽快恢复静止状态，需要对结构的残余振动进行控制，并通过结构优化实现最佳的减振效果. Yan等[1]针对旋转运动柔性梁的残余振动给出了控制方案. 该方案通过结合输入整形技术和附着在梁上的压电驱动器实现降低结构残余振动的目的. Yang等[2]基于等效静力法以最小化残余振动峰值为目标研究了高速加工设备柔性臂的结构拓扑优化设计.

可以通过二次型积分形式的性能指标衡量结构残余振动的大小. 然而，积分形式的性能指标的计算是非常困难的. 基于李雅普诺夫方程[3]可以大幅的简化该性能指标的表达式. Wang等[4]应用李雅普诺夫第二方法解决线性系统受初始激励的瞬态响应优化问题. Dong[5]将李雅普诺夫方程用于研究阻尼器的最优参数的解析计算方法，分别考虑了主结构有阻尼与无阻尼2种情况. Rüdinger[6]基于李雅普诺夫方程获得了白噪声下的非线性的调谐质量阻尼器的最优参数. 在以上的研究中，基于Lyapunov方程简化后的性能指标不仅有效的减少了计算的困难，还使得灵敏度计算变得容易实现.

灵敏度计算是基于梯度的优化算法的基础. 计算灵敏度的方法有解析法、差分法和半解析法. 按照灵敏度的解析公式编程计算时，需要了解所采用的有限元的单元刚度矩阵的详细列式，在很多情况下是很困难的. 程耿东等[7]、Cheng等[8]、Haftka等[9]等提出采用半解析法计算灵敏度. Cheng等[10]深入研究了半解析法灵敏度分析的非正常误差，包括其刚体转动判据和消除方法. 半解析法已被证实是一种有效的求解灵敏度的方法，具有易编程、高计算效率等特点，得到了广泛的应用.

组合结构是指由杆梁板壳三维连续体等结构元件组成的结构. 实际的工程结构，例如桥梁、房屋建筑、船舶等，都是组合结构. 采用有限元法分析组合结构时需要采用多种类型单元，例如杆单元、梁单元、膜单元、板单元、壳单元和三维实体单元，并且将它们采用一定方式连接起来. 组合结构的优化需要解决包含多种类型单元的结构的分析、灵敏度计算及优化，有特殊的困难[11-13]. 20世纪80年代，钱令希、钟万勰、隋允康等开发了多单元、多工况、多约束的组合结构优化程序DDDU[14-16]，其中特别克服了包括梁单元在内的多种单元相关的灵敏度分析. 本文研究以最小化结构残余振动为目标的组合结构优化设计，基于半解析法实现了Yan等[17]提出的伴随法灵敏度的计算. 并借助Ansys与Matlab等商用软件实现半解析灵敏度计算与优化流程[18]，并计算了一个篮球架结构的优化设计以展示本方法.

1 残余振动最小化结构优化设计问题

受初始激励作用结构(无外力)的动力学控制方程为

(1)

(2)

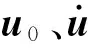
残余振动最小化结构优化设计问题的目标是寻找设计变量d使一个二次型积分形式目标函数值最小，

(3)

式(3)所示的目标函数可采用Lyapunov第二方程大幅地简化其计算.

为了应用Lyapunov第二方程，需将动力学控制方程与目标函数表达式转化到状态空间

(4)

(5)

利用式(4)，式(3)中的目标函数J可写成

(6)

对于线性渐近稳定系统，对于任给的正定对称系统Q，存在一个正定对称矩阵P满足Lyapunov方程

ATP+PA=-Q

(7)

在式(7)的基础上进行简单运算，可得到

(8)

根据式(8)，式(6)可进一步表示为

X(0)TPX(0)-X(∞)TPX(∞)

(9)

考虑系统的所有自由度都受到阻尼，残余振动会逐渐减少为零，即X(∞)TPX(∞)→0. 目标函数可表示为

J=X(0)TPX(0)

(10)

这样，用二次型积分形式衡量的残余振动最小化结构优化设计问题可写成

find(d1,d2,…,dM)

(11a)

minJ=X(0)TPX(0)

(11b)

s.t.ATP+PA=Q

(11c)

(11d)

other constraints

(11e)

式中：d1、d2、dM为设计变量，共M个设计变量. 有的残余振动最小化结构优化设计问题还会包含其他的约束条件，鉴于篇幅所限，本文将不深入讨论.

2 灵敏度分析

2.1 伴随法灵敏度分析

对于如式(10)所示的表达式，若初始条件X(0)与设计变量无关，则可以采用基于伴随法的计算方法求解J关于设计变量的灵敏度，其计算式为

(12)

Aλ+λAT+X(0)X(0)T=0

(13)

(14)

求得. 需要指出的是，按照上述方法计算灵敏度时，无论多少设计变量，求解两次Lyapunov方程(式(7)(13))即可获得目标函数关于所有设计变量的灵敏度. 因此，当优化问题包含了多个设计变量时，选择该方法可以有效地减少灵敏度计算的耗时. 然而，当分析模型的自由度很多时，Lyapunov方程的求解将是十分耗时的. 对于这种情况，模型降阶是一种有效的解决方法. 降阶方法中，模态降阶法是一种经常被使用的简便高效的模型降阶方法.

本文中将采用模态降阶法缩减分析模型的规模. 关于该方法的详细情况可以参考文献[19].

2.2 半解析法实现伴随法灵敏度分析

对于包含了多种单元类型与众多局部坐标系的组合结构，编程实现仍然很困难. 为了克服上述难点，本文基于参数化的有限元模型，通过差分法计算

(15)

灵敏度计算流程如图1所示. 基于得到的灵敏度可以进行结构优化设计. 优化流程如图2所示.

3 数值算例

数值算例考虑了一个由板梁组合构成的篮球架结构，如图3所示. 数值模型的尺寸是参照JN- 0304移动篮球架设计规范设定的. 采用Ansys分析时，该结构的有限元模型包含了141个BEAM188型梁单元、590个SHELL63型壳单元，共有824个节点，每个节点6个自由度. 结构的全部部件采用相同的材料，弹性模量为210 GPa，泊松比为0.3，密度为7 850 kg/m3. 研究中，基于模态降阶法采用结构的前100阶模态振型构造降阶模型以减少分析模型中的自由度数目. 篮球架结构的底面固支，结构承受的初始激励为篮板与篮框的z方向初速度为0.1 m/s.

优化问题的设计变量为1号板、2号板的厚度以及1号板与2号板的夹角α(1号板位置不变)，2号板与3号板的长度，共5个设计变量，如图4所示. 约束条件为1号板、2号板与3号板的材料用量之和不变. 厚度(mm)设计变量取值需位于[5，30]，角度设计变量取值需位于[125°，180°]. 3号板与2号板具有相同的厚度.

注意到，由于篮球架的使用需求，篮筐的高度是不能任意改变的. 本算例设定，优化过程中，3号板与水平面夹角以及3号板与篮板的交线(L4)位置不变，从而3号板与2号板的交线(L3)位置将随α改变而改变，1号板与2号板的交线(L2)位置保持不变同时其与2号板左端(L1)的距离保持不变. 因此，2号板与3号板的长度虽然是设计变量，但并不独立. 对于上述优化问题，解析的计算结构刚度阵、阻尼阵以及质量阵关于设计变量的灵敏度是非常困难的，但基于半解析法则可方便的克服上述困难.

本文将采用目标函数衡量篮球架的残余振动响应，目标函数为

(16)

式中：uj为篮板以及篮筐上节点的z方向位移；Na为篮板与篮筐的节点的总数.

经比较测试，本算例中将采用Δdi=0.01作为半解析法计算时的摄动量. 基于本文的优化方法的优化过程的迭代历史如图5所示.

表1中汇总了初始设计与优化设计的设计变量取值以及目标函数值等信息. 结果显示，基于本文的优化方法可以有效地减小结构的残余振动响应.

比较初始设计与优化设计的设计变量取值可以发现，1号板厚度减小，而2号板则厚度增加并为设计变量的取值上限，因此增加2号板的厚度比增加1号板的厚度对减小结构的残余振动的帮助更大. 优化设计在材料用量相同的情况下将残余振动减小了约90%.

最后基于瞬态动力分析结果验证获得的优化设计是否是合理的. 图6中比较了初始设计与优化设计下的点A(位置如图3所示)的位移时程响应. 结果显示，优化设计下的残余振动的衰减速度明显优于初始设计. 这说明基于本文提出的方法获得的优化设计是有效的.

表1 初始设计与优化设计的设计变量取值以及目标函数值

4 结论

本文研究了以残余振动最小化为目标的组合结构优化设计问题. 研究中采用半解析灵敏度计算方法克服了难以解析计算组合结构的K、M、C关于设计变量的偏导矩阵的困难. 基于参数化建模技术，通过Matlab与Ansys软件的二次开发功能实现了半解析灵敏度计算与优化迭代过程. 最后，数值算例中考虑了一个篮球架模型的残余振动最小化优化设计问题. 结果显示，在材料用量相同的条件下，优化设计的残余振动显著的小于初始设计. 该结果验证了程序及方法的有效性.

[1] YAN A Z, WANG G Q, XU H, et al. Reduction of residual vibration in a rotating flexible beam[J]. Acta Mechanica, 2004, 171(3/4): 137-149.

[2] YANG Z J, XIN C, ROBERT K. A topological optimization approach for structural design of a high-speed low-load mechanism using the equivalent static loads method[J]. International Journal for Numerical Methods in Engineering, 2012, 89(89): 584-598.

[3] KALMAN R, BERTRAM J. Control system analysis and design via the second method of Lyapunov: (Ⅰ) continuous-time systems (Ⅱ) discrete time systems[J]. Ire Transactions on Automatic Control, 1959, 4(3): 112-112.

[4] WANG B P, KITIS L, PILKEY W D. Transient response optimization of vibrating structures by Lyapunov’s second method[J]. Journal of Sound & Vibration, 1984, 96(4): 505-512.

[5] DONG D. Analytical solutions for DVA optimization based on the Lyapunov equation[J]. Journal of Vibration & Acoustics, 2008, 130(5): 1537-1538.

[6] RÜDINGER F. Optimal vibration absorber with nonlinear viscous power law damping and white noise excitation[J]. Journal of Engineering Mechanics, 2006, 132(1): 46-53.

[7] 程耿东, 汪榴. 旋转体形状优化及敏度分析的拟解析法[J]. 大连理工大学学报, 1986,25(3):15-25. CHENG G D, WANG L. Shape optimization of axisymmetric body and sensitivity analysis by quasi-analytical method[J]. Journal of Dalian University of Technology, 1986,25(3):15-25. (in Chinese)

[8] GHENG G D, LIU Y W. A new computation scheme for sensitivity analysis[J]. Engineering Optimization, 1987, 12(3): 219-234.

[9] BARTHELEMY B, CHON C T, HAFTKA R T. Accuracy problems associted with semi-analytical derivatives of static response[J]. Finite Elements in Analysis & Design, 1988, 4(3): 249-265.

[10] CHENG G D, GU Y X, ZHOU Y Y. Accuracy of semi-analytic sensitivity analysis[J]. Finite Elements in Analysis & Design, 1989, 6(2): 113-128.

[11] 隋允康， 杜家政， 郭英乔. 无量纲的框架结构截面优化[J]. 北京工业大学学报， 2004， 30(增刊)：24-28. SUI Y K, DU J Z, GUO Y Q. Dimentionless sectional optimization of frame structures[J]. Journal of Beijing University of Technology, 2004, 30(Suppl): 24-28. (in Chinese)

[12] 隋允康, 张伟, 杜家政. 多单元组合结构截面强度优化[J]. 北京工业大学学报, 2007, 33(2): 113-118. SUI Y K, ZHANG W, DU J Z. Sectional area optimization subjected to strength constraints for structures combined by multiple elements[J]. Journal of Beijing University of Technology, 2007, 33(2): 113-118. (in Chinese)

[13] 杜群贵， 迟永滨. 通用结构优化设计系统的研究与实现[J]. 机械， 2001， 28(6)：22-24. DU Q G, CHI Y B. Research on a universal structure optimization system[J]. Machinery, 2001, 28(6): 22-24. (in Chinese)

[14] 钱令希， 钟万勰， 隋允康， 等. 多单元、多工况、多约束的结构优化设计：DDDU程序系统[J]. 大连工学院学报， 1980， 19(4)：1-17. QIAN L X, ZHONG W X, SUI Y K, et al. Optimum design of structures with multiple typer of element under multiple loading cases and multiple constraints: program system DDDU[J]. Journal of Dalian University of Technology, 1980, 19(4): 1-17. (in Chinese)

[15] QIAN L X, ZHONG W X, SUI Y K. Efficient optimum design of structure: program DDDU[J]. Computer Methods in Applied Mechanics and Engineering, 1982, 30(2): 209-224.

[16] 隋允康， 钟万勰， 钱令希. 杆- 膜- 梁组合结构优化的DDDU-2程序系统[J]. 大连工学院学报， 1983， 22(1)：21-36. SUI Y K, ZHONG W X, QIAN L X. Optimum design of structures composed of bars-membranes-beams program system DDDU-2[J]. Journal of Dalian University of Technology, 1983, 22(1): 21-36. (in Chinese)

[17] YAN K, CHENG G D, WANG B P. Adjoint methods of sensitivity analysis for Lyapunov equation[J]. Structural & Multidisciplinary Optimization, 2016, 53(2): 225-237.

[18] 陈敏, 隋允康, 阳志光. 基于多种语言混合编程的优化软件设计[J]. 计算机工程与设计, 2008, 29(16): 4380-4382. CHEN M, SUI Y K, YANG Z G. Design of optimization software based on mixed programming with multi-codes[J]. Computer Engineering & Design, 2008, 29(16): 4380-4382. (in Chinese)

[19] 库克. 有限元分析的概念与应用[M]. 西安: 西安交通大学出版社, 2007: 341-344.

(责任编辑 杨开英)

Optimization Design of Structure Subject to Impact for Minimization of Residual Vibration

YAN Kun1, LIU Xiaode2, CHENG Gengdong1

(1.State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116023, China; 2.Department of Mechanics and Engineering Science, Peking University, Beijing 100871, China)

External impact on engineering structure generates residual vibration, which may deteriorate structural performance. This paper studies optimum design of combined structure subject to impact for minimization of residual vibration. The objective function of the optimization problem is a performance index in the form of the integral of a quadratic function, which measures the residual vibration response globally. The design variables are geometric parameters of combined structure including size, shape and layout of the structure and its members. Due to the complexity of the stiffness matrix and mass matrix of the combined structure, a semi analytical sensitivity approach was implemented to overcome the difficulty of adjoint sensitivity evaluation. Both commercial software Matlab and Ansys were adopted to realize the semi-analytical sensitivity analysis and the optimization process. One numerical example demonstrates the effectiveness of the proposed method.

residual vibration；semi-analytic sensitivity method；combined structure; structure optimization

2016- 08- 16

国家自然科学基金资助项目(11332004)

阎 琨(1987—)， 男， 博士研究生， 主要从事结构优化设计方面的研究， E-mail: yankun@mail.dlut.edu.cn

程耿东(1941—)，男，中国科学院院士，俄罗斯科学院外籍院士，教授,博士生导师，主要从事工程力学、计算力学和结构优化设计方面的研究，E-mail: chenggd@dlut.edu.cn

O 328

A

0254-0037(2016)12-1775-06

10.11936/bjutxb2016080038