离散动力学数值积分应该保辛近似

钟万勰

(大连理工大学运载工程与力学学部， 大连 116023)



离散动力学数值积分应该保辛近似

钟万勰

(大连理工大学运载工程与力学学部， 大连 116023)

动力学离散后的数值积分应该保辛近似. 辛对称来源于Hamilton正则方程，而其对应的变分原理是最小作用量变分原理. 离散后成为保辛近似，而不应该用保结构等不确切的概念来代替. 保辛是冯康提出的成果，应当予以重视.

离散动力学；保辛近似；最小作用量原理

笔者出身于土木结构力学，相关研究是从结构力学与最优控制的模拟关系切入辛代数的. 笔者在文献[1]中指出：“离散后，西方权威提出‘不可积系统，保辛近似算法不能使能量守恒’的误判. 法国数学家泊松(Poisson)指出，n维位移的动力学系统有n个首次积分；能量守恒包含于其中. 能量，众所关注，但也仅是其中一个首次积分. 最小作用量变分原理导出的本是n对正则方程，再没有多余的. 最小作用量不能用一个能量守恒来代替n个首次积分本应全部守恒，问题在于分析解难以求出. 未能求出的分析解在离散时，并非不重要，只是未能分析求解. 离散时要‘保辛’是全面的近似提法；而国外学者只考虑能量保守，是不全面的，违反了最小作用量原理，也就离开了短程线的几何化提法了，对此可质疑：这还是正宗的动力学吗？国外学者的提法也是有误区的. ”

钱令希先生为文献[2]作序时指出：“力学工作者应首先虚心地汲取状态空间法成功的经验，重新认识哈密顿体系理论的深刻意义，以及随之而来的辛数学方法及其对应用力学的应用”. 表明了钱先生的高瞻远瞩，走对方向特别重要. 今天，常被提及的“精确打击”“反导”等军事术语表明了控制的重要性. 中国力学学会将过去的一般力学改名为动力学与控制. 动力学不是结构力学，文献[3]给出了动力学与结构力学的模拟关系. 因此，结构力学以及动力学与控制可在同一套哈密顿(Hamilton)体系的数学下予以处理. 而哈密顿体系正是在动力学范围内发展的.

自牛顿之后，n维动力学问题的求解是150多年研究的主题，产生了分析力学. 欧拉- 拉格朗日(Euler-Lagrange)给出了能量表达的拉格朗日函数及n维一类位移变量q(t)的变分原理. 然后，哈密顿引入了对偶变量q、p的体系. 提出了哈密顿正则方程

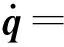
(1)

式中：n维向量q(t)、p(t)分别为位移与动量，相互对偶.

这些研究成果为相对论与量子力学奠定了数学基础. 因量子力学有光谱分析的需要，根据对偶正则方程的对称性，大数学家赫曼·外尔(Hermann Weyl)[4]提出了辛群对称：“The name ‘complex group’ formerly advocated by me in allusion to line complexes, … has become more and more embarrassing through collision with the word ‘complex’ in the connotation of complex number. I therefore propose to replace it by the Greek adjective ‘symplectic’. ” 表达了：为了避免“complex”容易产生的混淆，特地引入了希腊形容词“symplectic”予以顶替. 表明了“symplectic group”，辛群之意. 然而群论只能分析对称性，不能提供数值. 故本文属于动力学范围.

工程师需要数据. 由于动力学一般是非线性的，分析求解异常困难，故只能转而寻求数值求解，这只能离散后再求解. 将连续的时间坐标离散，就必然出现时间区段(ta,tb),ta

动力学数值求解经常拘泥于差分求解，大量的研究是差分格式的数值积分. 1985年，中国数学家冯康提出，差分格式应当“保辛”[5]. 这是针对离散近似求解的要求，从而得到了广泛关注. Hairer等[6]也注意到该成果，并且加以修改而称为“Geometric-Preserving”. 本文将就此修改，提出一些看法.

差分格式应“保辛”，既然讲差分，那就是离散后的近似. 其实中国古代数学家祖冲之(429—500)用割圆法计算圆周率，也是离散求解的，其精度已达π=3.141 592 6…. 可推测为，将圆周划分为内接m边正多角形，取m=2N,N=1,2,…,15.

图1所示为N=2→3的过渡.AB连线是N=2时的内接四边矩形.

如所熟知，平面几何两点之间的连接直线，就是最短距离，即短程线. 祖冲之用正多边形的总边长之和逼近圆周率. 注意到，短程线的直线，没有一点是满足约束条件的. 取短程线是根本不管约束条件的，只有在其两端，约束条件是严格满足的. 以上相应的处理不妨称之为祖冲之方法论.

动力学在状态空间q、p下的微分方程是正则方程式(1)，并且是可与两类变量的变分原理

(2)

互通的. 式中：S为区段(ta,tb),ta

祖冲之算法要在节点处满足约束条件；动力学位移约束条件，通常称为完整约束. 而通常的动力学没有约束条件，但并不妨碍短程线. 最小作用量原理给出的就是全部哈密顿正则方程. 而哈密顿正则方程正是赫曼·外尔提出辛群(symplectic group)的根据，表明最小作用量原理已经“保辛”了. 国外学者提出的“保结构”[6]对动力学来说，其概念模糊，在具体执行时片面地变成为保能量. 能量守恒本来只是n个首次积分之中的一个，一个首次积分无法代替最小作用量原理的全部n个首次积分，所以违反了最小作用量原理，就此质疑：不符合动力学的最小作用量原理，那还能说是正宗的动力学吗？

结论是，“保辛”才是动力学离散积分的全面提法，它代表最小作用量原理的短程线.

保辛是对于离散体系而言的，连续系统的解当然是本来就处处保辛. 然而因难以数值求解，只能寻求离散近似数值解. 近似解总得放弃些性质，而关键的性质不可放弃. 保辛的要求表明，离散时哈密顿体系的辛群对称性质是不可放弃的. 这是中国计算数学家冯康提出的在这个领域新的成果. 泊松提出，n维动力学系统有n个首次积分，问题是分析求解全部首次积分一般难以达到，不过也有若干个首次积分是可以分析求解的，例如能量守恒等. 那么离散数值积分时是否可以使能分析求解的首次积分也达到守恒呢？

国外名者[6]将“保辛”修改为“保结构”. 辛是专门名词，而结构代表什么还没讲清楚，是模糊概念. 因此，国内的科学家在动力学数值积分对于保辛的提法应引起足够的注意. 不要讲保结构等等的模糊概念，从而将冯康提出的正确概念和错误的提法相混淆，对于正确的概念我们是要继承的.

要首次积分达到守恒，只能在离散后的格点处. 因不在格点时，一般用简单的函数进行插值，难以同时使首次积分守恒. 首次积分一般是在状态空间表达的，将首次积分守恒作为约束条件，则成为非完整的约束. 非完整等式约束在数值积分时也是可让它保持守恒[7]，但计算量自然会增加.

通常，在数值积分时追求简单，因此常常采用最简单的例如时间有限元法. 即使如此，大量的数值例题表明，能量的偏离也很小，而且偏离了往往又能返回.

[1] 钟万勰. 主编寄语——中国应用数学的发展思路[J]. 应用数学与力学, 2016(3). ZHONG W X. Chief editor’s note—the development of Chinese applied mathematics [J]. Applied Mathematics and Mechanics, 2016(3). (in Chinese)

[2] 钟万勰, 欧阳华江, 邓子辰. 计算结构力学与最优控制[M]. 大连: 大连理工大学出版社, 1993.

[3] 钟万勰. 应用力学的辛数学方法[M]. 北京: 高等教育出版社, 2006.

[4] WEYL H. The classical groups: their invariants and representations [M]. Princeton: University Press, 1939.

[5] 冯康, 秦孟兆. Hamilton体系的辛计算格式[M]. 杭州: 浙江科技出版社, 2004.

[6] HAIRER E, LUBICH C, WANNER G. Structure-preserving algorithms for ordinary differential equations[M]. 2nd ed. Berlin: Springer, 2006: 479.

[7] 高强, 钟万勰. 非完整约束动力系统的离散积分方法[J]. 动力学与控制学报, 2012, 10(3): 193-198. GAO Q, ZHONG W X. Numerical algorithms for dynamic system with non-holonomic constrains [J]. Journal of Dynamics and Control, 2012, 10(3): 193-198. (in Chinese)

(责任编辑 杨开英)

Symplectic Conservative Approximation for Discrete Dynamics Integration

ZHONG Wanxie

(Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116023, China)

Symplectic conservation should be confirmed after discrete integration for dynamics. Symplectic symmetry is from Hamilton canonical equation and its variational principle is the minimum action variational principle. Symplectic conservative approximation is confirmed after discrete, and it should not be replaced by inaccurate concept such as structure-preserving. Symplectic conservation was proposed by Kang Feng, which should be taken seriously.

discretized dynamic system; symplectic conservation; minimum action variational principle

2016- 06- 30

钟万勰(1934—)，男，中国科学院院士，主要从事计算力学理论与应用方面的研究，E-mail: wxzhong@dlut.edu.cn

O 313

A

0254-0037(2016)12-1772-03

10.11936/bjutxb2016060088