缝洞介质内非达西流动实验研究
2016-12-21刘慧卿郭小倩
杨 阳, 刘慧卿, 张 萌, 谢 灵, 郭小倩
(1.中国石油大学(北京) 石油与天然气工程学院,北京 102249; 2.中国石油勘探开发研究院,北京 100831;3.中国石油华北油田分公司,河北 廊坊 065000; 4.中国石油天然气管道局天津设计院,天津 300457)
缝洞介质内非达西流动实验研究
杨 阳1,2, 刘慧卿1, 张 萌3, 谢 灵1, 郭小倩4
(1.中国石油大学(北京) 石油与天然气工程学院,北京 102249; 2.中国石油勘探开发研究院,北京 100831;3.中国石油华北油田分公司,河北 廊坊 065000; 4.中国石油天然气管道局天津设计院,天津 300457)

采用熔蜡的方法制作了多组全直径缝洞岩心,并利用岩心进行了一系列单相水流动实验,研究缝洞岩心内的流体流动规律。利用单相流动实验结果,采用多参数拟合方法得到适用于缝洞介质的非达西系数表达式,计算了缝洞介质的临界福西海默数(Fo)和临界非达西效应误差。研究结果表明:在矿场的水线推进速度下,压力降与流速存在线性和非线性关系,因此流体的流动规律存在达西流动和高速非达西流动,而其中更多的是高速非达西流动,这主要取决于裂缝的发育程度;Geertsma提出的非达西系数经验公式对于缝洞介质的适用性很差,本文在其基础上修正的非达西系数表达式适用于缝洞介质;缝洞介质的临界福西海默数在0.65±0.1范围内,远远大于砂岩介质的临界Fo,临界非达西效应高达35%~45%,表明非达西效应在缝洞介质中的不可忽略性。
缝洞介质; 全直径岩心; 非达西系数; 福西海默数
0 引 言
缝洞型油藏占全球碳酸盐岩油藏的30%以上,我国未来石油开采的主战场——塔河油田也属于缝洞型油藏[1-3]。缝洞油藏中,流体在裂缝和溶洞中运移和储存,基质几乎不具备储渗能力[4-6]。裂缝发育程度高、倾角大,溶洞分布随机、尺寸大等特点是多年来国内外学者对缝洞油藏的普遍认识[7-8]。近年来,许多学者开展了缝洞介质物理模型实验研究,但是所采用的物理模型多为规则或近似,很难正确反映缝洞介质内流体的流动规律,或是并没有重视流体的非达西流动规律[9]。本文采用熔蜡法制备全直径缝洞岩心,更真实地反映缝洞油藏特征,并进行非达西流动实验,研究缝洞介质中单相流体流动规律、非达西系数和临界Fo等重要参数。
1 缝洞岩心流动规律实验
全直径岩心主要由碳酸盐岩粉末和石灰混合组成,其中石灰起胶结作用[10]。为了降低岩心的脆性,减少在造缝、洞时对岩心的损坏,制备过程中加入了适量预糊化淀粉。人造缝洞岩心的制备过程主要包括:①蜡块、石灰粉、碳酸盐岩粉末和预糊化淀粉的混合物与水按照适当比例搅拌均匀后灌入模具中,见图1(a);②凝固后,利用岩心切割机随机高角度切割模型,把切割下的每一部分放入80 ℃的恒温箱中进行熔蜡处理,见图1(b);③在切割的两面黏贴适量铜片,最后按照原来的切割方式重新将各部分黏合,见图1(c)。这样,岩心中的裂缝开度、洞径可以被铜片厚度、蜡块直径所控制,见图1(d)。

(a)(b)(c)(d)
图1 全直径岩心制备过程
实验系统如图2所示,主要包括流体供给装置、全直径岩心夹持装置和测量装置三部分。抗高压中间容器中的水通过高精度平流泵驱动流入全直径岩心中;全直径岩心夹持器安置在大型恒温箱中,保证实验温度的稳定性;全直径岩心两端装有压力传感器,分别连接在数据采集系统上,用来记录系统稳定后的进、出口端压力。实验所用流体为黏度1 mPa·s的蒸馏水,实验温度30 ℃,全直径岩心夹持器围压4 MPa,全直径岩心长30 cm,直径10 cm。实验岩心的其他物性参数如表1所示。
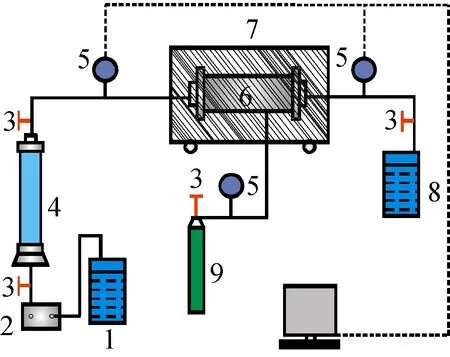
1-容器,2-平流泵,3-阀门,4-水容器,5-压力传感器,6-岩心夹持器,7-恒温箱,8-集液器,9-氮气瓶,10-数据采集

图2 实验系统示意图
当注水速度0.25~10 mL/min时,计算水线推进速度为32~145 m/d,该速度在缝洞油藏现场正常注水推进速度范围(30~150 m/d)之内[11]。图3和图4为实验岩心的压力降和流速关系图。表明在缝洞油藏水区时,裂缝开度很小,流体流动规律符合达西定律(见图3);裂缝开度较大时,流体流动规律为非达西流动(见图4)。

图3 注水速度与压力降线性关系图

图4 注水速度与压力降非线性关系图
2 非达西系数修正
Forchheimer首先发现了非达西现象,提出了著名的Forchheimer方程[12]。2005年, Barree等忽略了重力的影响,重新改写了公式[13]:
(1)



Geertsma通过300多块岩心测量数据,包括松散砂岩、致密砂岩、裂缝孔隙型石灰岩和裂缝型石灰岩,进行量纲分析后得到非达西系数的经验关系式[14]:
(2)
式中:K为渗透率, cm2;φ为岩心孔隙度。

表2 全直径岩心物性参数
由图6可见,当裂缝、溶洞尺寸较小时(岩心2,3),Geertsma经验公式勉强能拟合实验结果;随着裂缝、溶洞尺寸的增大(岩心5,6,8,9),Geertsma经验公式计算结果和实验结果的偏差逐渐增大。这可能是由于缝洞介质较大的储渗空间导致的孔隙结构更加复杂、非均质更强所致。因此,本文针对缝洞结构,引入缝、洞特征参数,对Geertsma经验公式进行了修正:
(3)
式中:d为洞径,mm;w为裂缝开度,mm;φv为洞孔隙度;φf为裂缝孔隙度。结果表明,式(4)计算结果与实验测量的非达西系数值拟合较好,其相对误差小于4.39%,如图6所示。

图6 非达西系数对比图
3 临界福西海默数(Fo)
Fo是判别流态的一种标准,它的物理意义为惯性阻力与黏滞阻力之比,表达式为[15]:
(4)
为了判别达西流和非达西流,本文重新改写了Forchheimer方程:
(5)
(6)
以全直径岩心9为例,图7显示了Fx与Fy关系的斜率变化,即非达西系数的变化。定义β2为较低Fx值时的斜率,即拐点之前的斜率;β1为较高Fx值时的斜率,即拐点之后的斜率。则β2/β1表征了非达西系数的变形程度。拐点表征流体由部分非达西流动转变为全部非达西流动。因此,拐点的Fo即为临界Fo:
(7)
式中,vc为拐点速度。

图7 Fx与Fy关系图
非达西效应误差E定义为克服惯性阻力,压力梯度与总压力梯度之比[16]:
(8)
联立式(4)和(8),可得:
(9)
其可以在油藏数值模拟中成为模型是否考虑非达西效应的标准。联立式(7),用Ec表示临界非达西效应误差:
(10)
表3显示了在现场正常注水推进速度范围内,流动规律为非达西流动的实验岩心的临界福西海默数、临界非达西效应误差和非达西系数的变形程度。一般砂岩介质的临界非达西效应误差取10%,对应的临界Fo为0.11[17]。然而本文实验结果表明缝洞介质的临界Foc=0.65±0.1,相应的临界非达西效应误差范围在35%~45%,这远比砂岩介质要大得多。导致这样的原因可能是缝洞介质较高的孔隙度和渗透率,它们严重影响着流体在介质中的流动规律。

表3 全直径岩心临近福西海默数和临界非达西效应误差
4 结 论
(1)在缝洞油藏现场正常注水推进速度范围内,流体流动可能符合达西定律,也可能符合非达西流动规律。由于在缝洞介质中,裂缝是流体流动的主要通道,因此流动规律主要取决于裂缝的开度。同时,实验结果也表明,在裂缝开度较小时,为达西流动;反之,为非达西流动。
(2)利用多参数拟合的方法修正了Geertsma经验公式,得到了适用于缝洞介质的非达西系数计算公式,其计算结果与实验结果拟合较好,相对误差小于4.39%。
(3)通过实验标定了缝洞介质的Foc和临界非达西效应误差,分别为Foc=0.65±0.1,Ec=35%~45%,远大于砂岩介质。因此,在缝洞介质中,非达西效应是不可忽略的。
[1] 吕爱民. 碳酸盐岩缝洞型油藏油藏工程方法研究[D]. 东营: 中国石油大学(华东), 2013.
[2] 李 阳. 塔河油田碳酸盐岩缝洞型油藏开发理论及方法[J]. 石油学报, 2013, 34(1): 115-121.
[3] 鲁新便, 蔡忠贤. 缝洞型碳酸盐岩油藏古溶洞系统与油气开发——以塔河碳酸盐岩溶洞型油藏为例[J]. 石油与天然气地质, 2010, 31(1): 22-27.
[4] 杜金虎, 周新源, 李启明, 等. 塔里木盆地碳酸盐岩大油气区特征与主控因素[J]. 石油勘探与开发, 2011, 38(6): 652-661.
[5] 胡向阳, 袁向春, 侯加根, 等. 多尺度岩溶相控碳酸盐岩缝洞型油藏储集体建模方法[J]. 石油学报, 2014, 35(2): 340-346.
[6] Peng X L, Du Z M, Liang B S,etal. Darcy-Stokes Streamline Simulation for the Tahe-Fractured Reservoir With Cavities[J]. SPE Journal, 2009,14(3): 543-552.
[7] Popov P, Bi Linfeng, Efendiev Y,etal. Multiphysics and multiscale methods for modeling fluid flow through naturally fractured vuggy carbonate reservoirs[J]. SPE, 2007: 105378.
[8] 李 阳, 范智慧. 塔河奥陶系碳酸盐岩油藏缝洞系统发育模式与分布规律[J]. 石油学报, 2011, 32(1): 101-106.
[9] 王 雷, 窦之林, 林 涛, 等. 缝洞型油藏注水驱油可视化物理模拟研究[J]. 西南石油大学学报(自然科学版), 2011, 33(2): 121-124.
[10] 王 敬, 刘慧卿, 徐 杰, 等. 缝洞型油藏剩余油形成机制及分布规律[J]. 石油勘探与开发, 2012, 39(5): 585-590.
[11] 郑小敏, 孙 雷, 王 雷, 等. 缝洞型碳酸盐岩油藏水驱油机理物理模拟研究[J]. 西南石油大学学报(自然科学版), 2010, 32(2): 89-92.
[12] Forchheimer P. Wasserbewegung durch boden[J]. Z Ver Deutsch Ing, 1901, 45: 1782-1788.
[13] Barree R D, Conway M W. Reply to Discussion of “Beyond Beta factors: A complete model for Darcy, Forchheimer, and Trans-Forchheimer flow in porous media” [J]. J Pet Tech, 2005, 53(8): 73-74.
[14] Geertsma J. Estimating the coefficient of inertial resistance in fluid flow through porous media[J]. SPEJ, 1974, 14(5): 445-450.
[15] Ma H, Ruth D W. The microscopic analysis of high Forchheimer number flow in porous media[J]. Transp Porous Media, 1993, 13: 139-160.
[16] Zeng Z, Grigg R. A criterion for non-Darcy flow in porous media[J]. Transp Porous Media, 2006, 63: 57-69.
[17] 卢占国. 缝洞型介质流体流动规律研究[D]. 东营: 中国石油大学(华东), 2010.
Experimental Investigation of Non-Darcy Flow in Artificial Frac-vuggy Media
YANGYang1,2,LIUHui-qing1,ZHANGMeng3,XIELing1,GUOXiao-qian4
(1.MOE Key Laboratory of Petroleum Engineering, Beijing 102249, China; 2.Petro China Research Institute of Petroleum Exploration & Development, Beijing 100831, China; 3.Petro China Huabei Oilfield Company, Langfang 065000, China; 4.China Petroleum Pipeline Bureau Tianjin Design Institute, Tianjin 300457, China)
Several groups of whole diameter frac-vuggy cores were made by using molten wax method. We did a series of single-phase water flow experiments to study the flow regime in frac-vuggy media. Based on the experimental data, non-Darcy flow coefficient expression was obtained by multi-parameter fitting method and applicable to frac-vuggy media. In addition, the critical Forchheimer number and the error of critical non-Darcy effect were obtained in frac-vuggy media. The results shows: both Darcy flow and non-Darcy flow behaviors exist in fracture-vuggy media under field water injection speed. And the flow regime depends on the fracture width. The non-Darcy flow coefficient expression was proposed and more applicable than Geertsma's in frac-vuggy media. Critical Forchheimer number ranges from 0.55 to 0.75 in frac-vuggy media, which is higher than that previous literature reported. The error of critical non-Darcy effect ranges from 35% to 45% and cannot be ignored.
frac-vuggy media; artificial frac-vuggy core; non-Darcy flow coefficient; Forchheimer number
2015-11-02
国家科技重大专项资助项目(2011ZX05014-003-004)
杨 阳(1988-),男,河北任丘人,在读博士,主要从事油藏数值模拟、提高采收率等方面研究。
Tel.:010-89731163;E-mail: whitesheep00@163.com
刘慧卿(1966-),男,河南台前人,教授,博士生导师,主要从事油藏数值模拟、稠油热采等方面研究。
Tel.:010-89731163;E-mail:liuhq@cup.edu.cn
TE 3
A
1006-7167(2016)08-0075-04
