供应链风险发生大小、发生与持续时间的估计：一个动态贝叶斯的推理网络研究范式

郑小京

文章编号：1001-148X（2016）08-0163-08

摘要：供应链风险具有多源性、多维性、传递性以及动态性的特点，准确评估其发生的概率以及发生与持续时间的可能性非常关键。为了实现这一目标，本文根据供应链风险的特征，构建了一个动态贝叶斯网络模型，利用极大似然法对该模型参数进行估计，并采用贝叶斯推理的方法估计特定条件下供应链风险的特征，结果发现供应链风险随着时间动态变化，但都收敛到一个稳定的概率区间。

关键词：供应链风险；可能性；发生时间；持续时间

中图分类号：F274文献标识码：A

收稿日期：2016-05-05

作者简介：郑小京（1975-），男，陕西白水人，哈尔滨商业大学商业经济研究院副研究员，管理学博士，研究方向：供应链管理。

基金项目：黑龙江省哲学与社会科学基金项目，项目编号：11D071；黑龙江博士后科研基金项目，项目编号：LBH-Z15109；哈尔滨商业大学博士科研启动基金项目，项目编号：13DW007。

对风险评价的本质在于试图分析风险发生的统计规律，因为统计规律可以发现其关键的可控风险因素，以及风险因素与风险之间的一个基本映射关系。但是，如果考虑风险的动态性，这些结果就很难描述供应链风险的多源性、多维性以及相互交叉性、传递性、动态性、非线性。本文拟构造一个供应链风险动态贝叶斯网络评估模型，通过这一模型分析供应链中若干风险之间的关系、若干风险可能的发生时间以及一旦发生可能持续的时间，试图得到一些有价值的结论。

一、供应链风险的特征及其贝叶斯网络刻画

如文献[1]、[5]、[12]所述，供应链风险具有高度的多源性和多维性，其风险因素与供应链若干风险之间形成非常复杂的关系，这种关系可以用一个贝叶斯网络来描述。

（一）供应链风险贝叶斯网络模型

根据供应链风险系统的特征，我们构建一个对应的供应链风险动态贝叶斯网络推理模型，描述供应链风险因素变化可能导致的供应链风险的性质、特征、状态及其变化。根据郑小京（2015）的研究成果，在分析的过程中，我们主要考虑以下风险的发生时机、发生可能性、持续时间所满足的性质：供应链核断裂、资金流断裂、物流断裂、牛鞭效应、道德风险、双重边际化。其中，关键可控的风险因素与重要风险及其关系用图1的贝叶斯网络模型来描述。

图1中，每个节点表示一种风险因素或风险事件，箭头表示他们之间的因果关系。这些节点的涵义依次为供应商可靠性随机、互补品随机扰动、替代品随机扰动、产品结构复杂性、供应链结构复杂性、非常规突发事件驱动的需求突变、供应商认可/选择不当、产品需求随机、产品需求分布特征变化、生产系统随机、信息共享结构不当、供给订单随机、生产过程序列随机、延迟制造随机性、生产成本方差随机、订单分配随机、合作预测无效、信息自身真实性随机、信息传递的扭曲程度、功能型产品信息管理系统崩溃、流行型产品信息管理系统崩溃、价格不确定、供应商库存管理无效、产品分派机制随机、供给契约参数随机波动、产品分派机制崩溃、供给契约中断、供应链核断裂、供应链网络崩溃、物流中断、双重边际化效应、牛鞭效应、资金链断裂、道德风险。通过贝叶斯网络，我们可以得到各个风险因素与风险之间错综复杂的关系以及对应的概率关系，这使得对供应链风险进行比较准确的估计有了数学基础。

实际上，供应链中风险因素对风险的影响表现出极强的非线性，不仅影响强度表现为随机时变性，而且风险因素结构与性质也具有随机时变性——在一开始对供应链风险影响较为重要的因素，当供应链发展到一种伪平衡状态时，这些因素将不是导致其爆发的关键因素，而可能是其中一个微不足道的因素的微弱变化将会导致供应链崩溃。本文所构造的动态贝叶斯网络模型完全可以描述这一供应链风险的动态性以及非线性特征，并通过分析把握供应链风险参数的性质，对这些供应链风险的参数进行推理，实现真正的评估。

（二）供应链风险动态贝叶斯网络模型

为了分析方便，不妨假定每一个风险因素或风险事件有三个状态：发生态、临界态以及未发生态，在不同的时间，它可以按照一定的规律由一种状态切换到另外一种状态上。如果能把握这一风险事件发生时间以及持续时间的可能性大小，供应链风险评估的准确性与科学意义就得以很大的提高。文献[13]构造了一个类似的模型，描述了一个简单的链状贝叶斯网络，但供应链风险贝叶斯模型比其复杂得多，且我们考虑的参数也有一些变化。

如前所述，供应链风险的发生与因素的状态有关系，而供应链风险因素的状态只有三种，即发生、不发生、临界态。一旦发生，将会引起下一个因素的变化，这种变化在供应链网络中进行传播，最终导致了供应链风险的非线性迭加效应——供应链风险复杂且具有较大的随机性。不妨假定供应链风险因素都不发生为供应链的第一种状态——未被激活的状态；供应链风险因素全都发生这一现象为第三种的状态——完全激活的状态；供应链风险因素处于临界状态这一现象为第二种状态——完全随机的状态。这三个状态中，从其中某一个供应链风险因素没有变化到随机变化，有下列参数可以描述：风险因素的状态、从一个状态到另外一个状态的持续时间、从一个状态切换到另外一个状态的概率等。

下面我们重点分析一下供应链风险因素的这三种状态。发生态表示风险因素完全偏离了正常的状态，未发生态表示风险因素处于正常状态，而对于临界态，直接描述比较困难，我们给出一个直观的描述方式。临界态其实指的是这一风险因素随时都可能偏离正常状态，这是一个不稳状态。徐绪松和郑小京（2012，2013）对供应链道德风险中的因素以及道德风险的临界状态进行了分析，这一结果以及分析过程可以测定在整个供应链风险系统中风险因素是否处于临界状态。

由于风险影响因素的重要性随着系统状态、环境的变化而不断变化，因此就某一特定的风险因素或风险事件而言都是对应的随机过程，不妨假设这一系统满足下列条件：

（1）假设在一个有限的时间内条件概率变化过程对所有的t是一致平稳的；

（2）假设动态概率过程是马尔科夫（Markovian）的，即满足

P（X（t+1）|X（1），X（2），…，X（t））=P（X（t+1）|X（t））（1）

也就是说，未来时刻的概率分布只与当前时刻有关，而与过去历史无关；

（3）假设相邻时间的条件概率过程是平稳的，即P（X（t+1）|X（t））与时间t无关，可以容易得到不同时间的转移概率P（X（t+1）|X（t））。

文献[1-6]证明供应链风险系统中各个风险因素以及风险基本满足这三个假设，因此可在随机过程的基础上研究供应链风险。除此之外，注意到任意的一个风险因素以及风险事件并不是单独存在着的，而是按照图1的网络相互影响，这种相互影响就使得问题更加复杂。鉴于此，我们引入下列动态贝叶斯网络推理模型来描述这一问题。

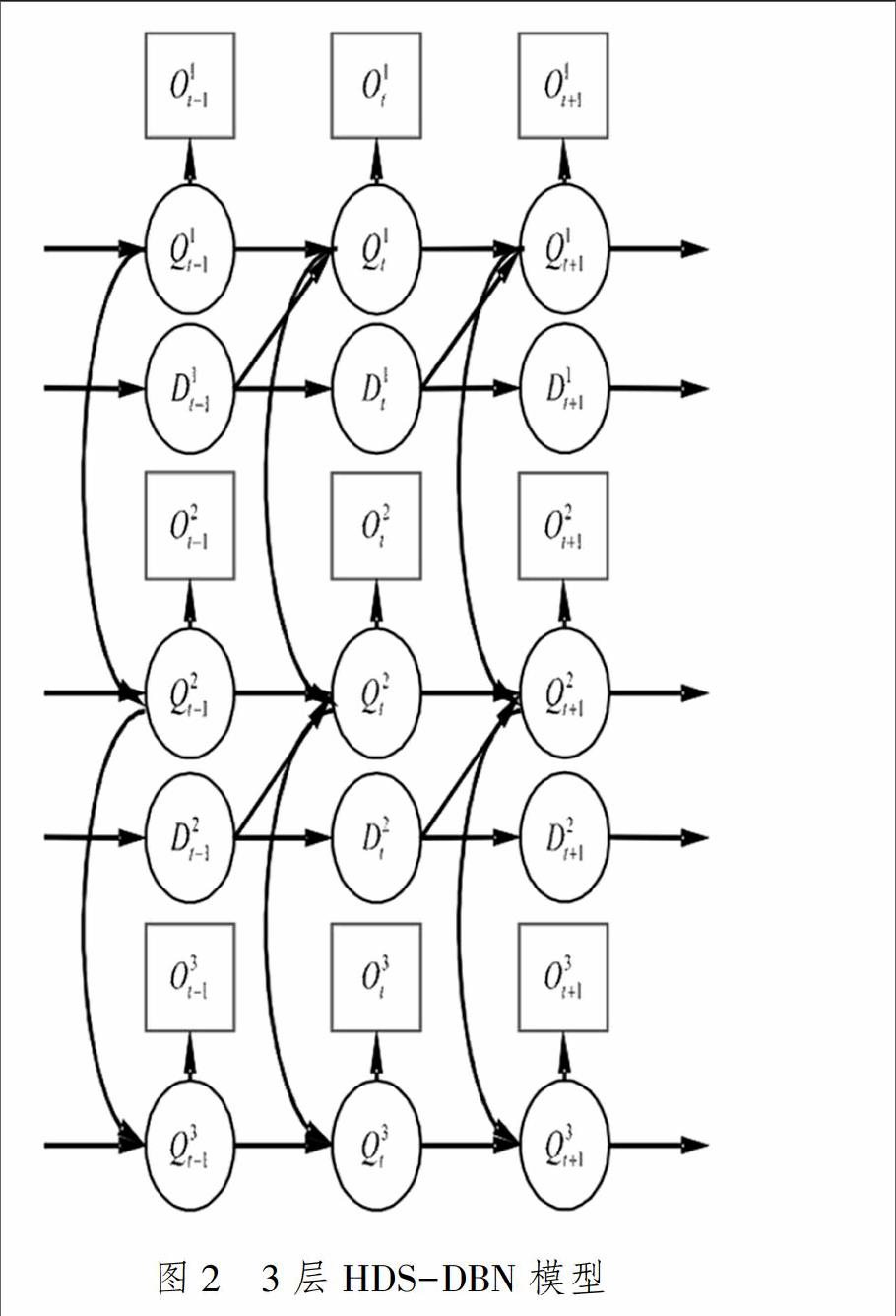
不失一般性，假设供应链风险贝叶斯网络可以被简化成一些有序排列的链条，按照箭头方向从尾部到头部的顺序对这些节点进行重新排序，得到新的编码，不妨记这一贝叶斯链节点集合为{1，2，…，L}。令M=（Q1：L，D1：L-1，O1：L，π1：L，A1：L，B1：L，P1：L-1）表示供应链风险系统，其中Q1：L，O1：L，D1：L-1分别表示节点1到节点L的行为状态、观测及节点1到节点L-1的驻留时间状态的集合。这是一个特殊的动态贝叶斯网络，其状态空间被分解成L个行为状态的集合Ql=1，2，3|Ql和L-1个驻留时间状态的集合Dl-1=d|d∈N∪0，其中N为自然数集。这一模型的参数Θ包括初始概率πl=πlij（节点l-1在初始时刻状态为i条件下，节点l状态为j的概率）、转移概率Al=alijk（节点l在时刻t-1上状态为j，且其驻留时间为d，以及节点l-1在时刻t状态为i条件下，节点l在时刻t状态为i的概率）、观测概率分布Bl=bli（Ot）（节点l在时刻t被观测到状态为i的概率分布）以及行为状态的驻留时间分布Pl-1=pl-1i（d）（节点l时刻t-1驻留时间为d条件下，在时刻t状态为i的驻留时间为d′的概率），其中l=1时，πlij和alijk可以退化成π1j和a1jk，即Θ=π1：L，A1：L，B1：L，P1：L-1。回顾图1描述的供应链风险贝叶斯图，可以发现，这一错综复杂的网络可以被简化成5条链状的贝叶斯链，这五条链的长度分别为12、13、13、14、13。将其最大值定义为供应链风险贝叶斯网络的直径，并用直径描述系统的层数。在本研究中，L=14，表示供应链在供给管理、需求管理、生产制造管理以及信息管理四个阶段的运作过程中对应的风险因素及风险的影响关系，同时也描述了一个风险因素的波动将会引起下一个风险因素的波动，并且这些因素或风险事件按照一定的概率在未发生态、临界态以及发生态等三种状态中随时间随机切换。这一模型比较复杂，为了直观地描述这一问题，图2给出一个只有三层的动态贝叶斯网络的情况。

从图1与图2可以看出，对于绝大多数风险因素以及所有的风险事件来说，它们的状态不仅受到这一风险因素自身状态的历史特性影响，而且还受到上一级风险因素状态影响；不仅如此，每一个风险因素的变化过程是一个马尔科夫过程。这种双重特性使得供应链风险变化比较复杂。

前面说明供应链风险动态贝叶斯网络可以分解成五条不同的链，对于每一条链来说，不妨假设其对应的风险因素或风险事件都是从1开始编号，一直到L结束（显然，这种编号简化了分析的复杂性，但绝不影响结果），那么在经典概率测度已知的前提下，这一模型的条件概率分布可以表示如下：

在图4中，实线表示道德风险，点虚线表示双重边际效应，短线段组成的虚线表示牛鞭效应，短线段与点组合成的虚线表示资金链断裂。横轴表示可能持续的时间，而纵轴表示可能发生的概率。从图4可以看出，这些风险发生持续时间很短时发生的可能性比较高，而当持续时间增长时，其可能发生的概率指数式降低，这一现象非常重要。另外，从图4中还可以看出牛鞭效应持续时间的分布情况出现了一个“奇异点”，这主要是因为道德风险的影响因素较为简单，正是由于这种单一的影响因素决定了它的持续时间可能与其他不一致。奇点的出现也比较正常，但是从总体上看，这一奇点可以忽略。

此外，持续时间是与发生时间紧密联系，知道了其中一个就可以得到另外一个的分布形式。这是因为一个时间最初发生时间与消失时间之间的差值就是这一风险的持续时间。如果我们仅仅考虑风险事件的状态在时间上的分布特征，这一风险发生与持续时间相关的结论就更加容易解释。根据概率的计算方法，不难知道，风险事件发生的时间分布形式也是一条类似的曲线。

三、 结论

供应链中存在着若干种类型的风险，他们之间并不独立存在，而是与供应链风险因素相互影响，形成了一个非常复杂的网络。这些供应链风险因素在任何一个时间点上都将随机出现发生、未发生以及临界等三种状态，并且每一种状态是完全独立的。每一种因素的特征将会影响它的下一个因素的状态，这种相互作用使得供应链风险的性质与状态非常复杂。本文构建了一个动态贝叶斯网络模型来描述这一供应链风险的特性，对其可能性大小、发生与持续时间等风险参数进行估计，并且就道德风险、牛鞭效应、双重边际化以及供应链资金链断裂等四种风险进行了研究，认为供应链风险并不是一个稳定的值，而是随着时间随机波动，不过这些风险将随着时间的推移收敛到一个比较确定的区域中。此外，在假定供应链风险因素都只出现发生与未发生两种情况的情形下，这些风险因素以及风险的持续时间的分布特征满足一个指数分布，其幂指数大小为所有风险因素以及风险发生概率的和。

参考文献：

[1]Christopher S. Tang. Perspectives in supply chain risk management[J].International of Production Economics，2006，103： 451-488.

[2]Claudia Colicchia and Fernanda Strozzi. Supply chain risk management： a new methodology for a systematic literature review[J].Supply Chain Management： An International Journal， 2012，17（4）： 403-418

[3]George A. Zsidisin， Bob Ritchie. Supply Chain Risk Management -Developments， Issues and Challenges[C].1-12. George A. Zsidisin， Bob Richie， Supply Chain Risk： A Handbook of Assessment， Management， and Performance. Springer Science+Business Media， LLC， 2009.

[4]Teresa Wu， Jennifer Blackhurst， Vellayappan Chidambaram.A model for inbound supply risk analysis[J].Computers in Industry，2006，57： 350-365.

[5]马建华，艾兴政，唐小我.多源不确定性因素下两阶段动态供应链的风险绩效[J].系统工程理论与实践，2012，32（6）：1222-1231.

[6]李民，黎建强. 基于模拟方法的供应链风险与成本[J].系统工程理论与实践，2012，32（3）：580-588.

[7]Steven A. Melnyk， Alexander Rodrigues， and Gary L. Ragatz. Using Simulation to Investigate Supply Chain Disruptions[C].103-122.George A. Zsidisin， Bob Richie， Supply Chain Risk：A Handbook of Assessment， Management， and Performance， Springer Science+Business Media， LLC， 2009.

[8]Bjrn Egil Asbjrnslett. Assessing the Vulnerability of Supply Chains[C].15-34. George A. Zsidisin， Bob Richie，Supply Chain Risk： A Handbook of Assessment， Management， and Performance， Springer Science+Business Media， LLC， 2009.

[9]Jukka Hallikas and Jari Varis. Risk Management in Value Networks[C].35-52. George A. Zsidisin， Bob Richie，Supply Chain Risk： A Handbook of Assessment， Management， and Performance， Springer Science+Business Media， LLC， 2009.

[10]Mohd Nishat Faisal， D.K. Banwet and Ravi Shankar. Mapping supply chains on risk and customer sensitivity dimensions[J].Industrial Management & Data Systems，2006，106（6）： 878-895

[11]Jennifer V. Blackhurst， Kevin P. Scheibe and Danny J. Johnson. Supplier risk assessment and monitoring for the automotive industry[J].International Journal of Physical Distribution & Logistics Management，2008，38（2）： 143-165.

[12]Archie Lockamy III， Kevin McCormack. Modeling supplier risks using Bayesian networks[J].Industrial Management & Data Systems，2012，112（2）： 313-333.

[13]杜友田，陈峰，徐文立.基于多层动态贝叶斯网络的人的行为多尺度分析及识别方法[J].自动化学报，2009，35（3）：225-232.

[14]郑小京.供应链风险评估：一个贝叶斯-量子决策的推理网络研究范式[J].哈尔滨商业大学学报，2014（6）.