相控阵卫星自跟踪系统闭环跟踪滤波研究
2016-12-20向晓萍黄宇声李朝海
向晓萍,黄宇声,李朝海
(电子科技大学 电子工程学院, 成都 611731)
·数据处理·
相控阵卫星自跟踪系统闭环跟踪滤波研究
向晓萍,黄宇声,李朝海
(电子科技大学 电子工程学院, 成都 611731)
为了在高速运动的载体上实现相控阵天线阵列波束始终对准卫星方向,对相控阵卫星自跟踪系统的总体框架和主要信号处理过程给出了说明。闭环跟踪滤波包括角度估计和跟踪滤波两个步骤,是卫星跟踪系统的核心处理模块,系统采用二维比相测角算法得到角度的估计值传入跟踪滤波算法中,将跟踪所得角度作为下一次测角的输入参数以形成闭环跟踪。研究了卡尔曼滤波、α-β滤波以及自适应α-β滤波三种跟踪滤波算法,给出坐标变换和野值剔除的方法,对于不同跟踪滤波方法下的系统跟踪精度给出仿真对比,并分析了不同场景下的α-β滤波算法性能。仿真结果表明:α-β滤波具有较高的跟踪精度,可以运用到高速移动的自跟踪系统。
相控阵;卫星跟踪;角度测量;跟踪滤波
0 引 言
卫星跟踪技术是通过某种跟踪手段,使得在载体运动的过程中,收发天线阵列波束始终对准卫星方向,以保证正确、稳定地完成与卫星之间信息传输的技术。相控阵天线扫描速度快、波束指向灵活且抗干扰能力强,能适应机动性较大的应用场景。
相控阵卫星跟踪系统涉及信号处理的多个领域,角度估计以及跟踪滤波是其中的两项关键技术。本文将结合工程应用,对相控阵卫星自跟踪系统闭环跟踪滤波进行研究,并对其中的跟踪滤波算法进行仿真分析,选择合适的滤波算法,利用测角加滤波的闭环跟踪过程实现对卫星目标位置的准确预测,控制天线波束对准目标信号[1],实现对目标信号的自动跟踪,最终使双向微波综合信道达到最佳的通信效果。
1 系统原理与架构设计
运动平台选用高速运动的弹载平台,将相控阵天线以及自跟踪处理单元安装在载体上。图1给出载体平台系统结构框图,图2为系统的工作流程。接收阵列在射频端合成4路子阵,4路子阵信号经预处理模块后,送入自跟踪单元。根据载体平台提供的姿态信息和引导信息完成卫星信号的搜索捕获和自跟踪,通过角度测量和跟踪滤波[2]等处理使得天线波束自动对准卫星。跟踪滤波过程中将实时检测目标是否跟丢,判定为跟丢后则重新转入搜索捕获状态。
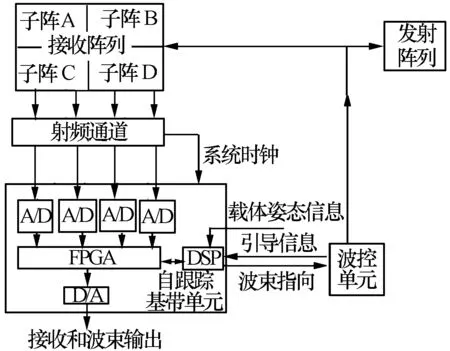
图1 载体平台系统结构框图
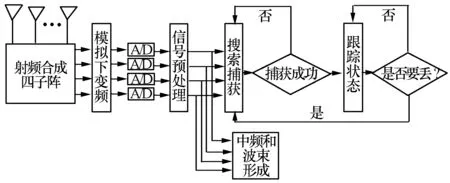
图2 系统工作流程
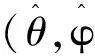
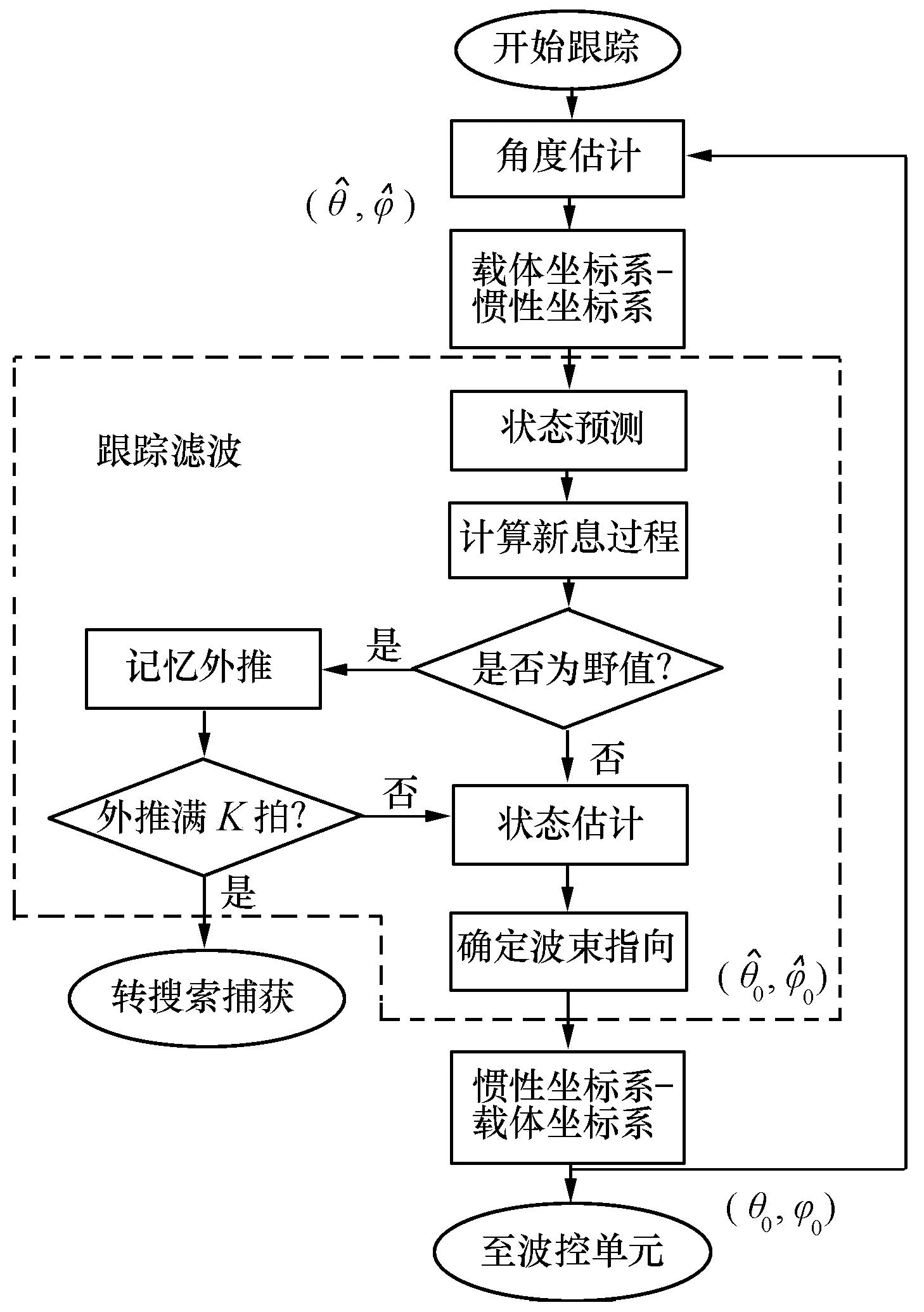
图3 自跟踪状态处理流程
在跟踪滤波处理中,受多种偶然因素影响,已跟踪到的目标仍然可能丢失。此时获得的角度估计值的误差较大,被称为野值,需进行剔除。若出现野值则按照先前的预测方向进行记忆外推。当连续出现多次野值时,则认为目标已经跟丢,此时应重新转入搜索捕获过程。
自动跟踪过程中选择子阵相关法[5]进行测角并跟踪滤波的闭环过程具有精确角度估计。下面将分析卡尔曼滤波、传统α-β滤波以及自适应α-β滤波三种跟踪滤波算法。给出坐标变换的方法,并建立运动场景,对于不同跟踪滤波方法下的系统跟踪精度给出仿真对比。
2 跟踪滤波算法原理分析
2.1 卡尔曼滤波算法
角度跟踪通常采用基于方向余弦的跟踪滤波算法。本系统中观测信息为卫星信号的入射角度[φ,θ]T。记[xcyczc]T为目标在惯性系下的方向余弦,其表达式为
[xcyczc]T=[sinθcosφ sinθsinφ cosθ]T
(1)
以方向余弦及其变化速度作为跟踪滤波器状态向量,记为
(2)
x轴、y轴和z轴三个维度的方向余弦变化速度可根据式(3)给出
(3)
式中:T为跟踪滤波器的采样周期。
离散化的目标运动状态方程为
x(n)=F(n,n-1)x(n-1)+Γ(n,n-1)v1(n-1)
(4)
式中:F(n,n-1)为状态转移矩阵,其取值为
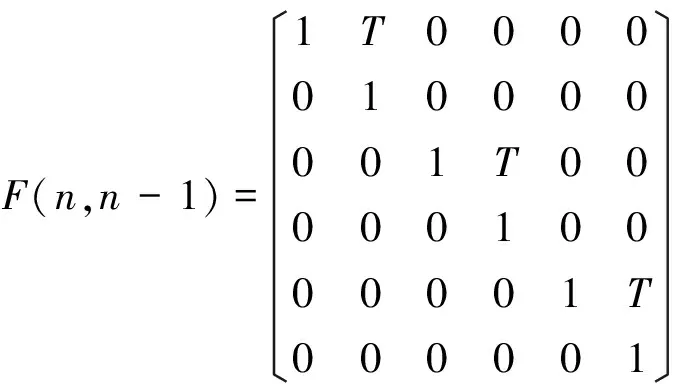
(5)
Γ(n,n-1)为状态噪声输入矩阵,取值为
(6)
v1(n)为该模型的状态噪声,也称为过程噪声,服从零均值、方差为Q1(n)的高斯分布。
观测方程为
z(n)=C(n)x(n)+v2(n)
(7)
式中:z(n)为观测向量,由x轴、y轴和z轴三个维度的方向余弦组成;v2(n)为观测噪声,服从零均值、方差为Q2(n)的高斯分布,它与过程噪声v1(n)相互独立;C(n)为观测矩阵,其取值为

(8)
卡尔曼滤波[6]的操作步骤如下:
步骤1:状态一步预测
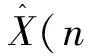
(9)
步骤2:根据观测向量z(n)求取新息过程
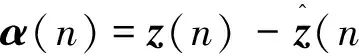
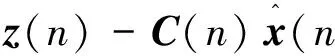
(10)
步骤3:计算一步预测误差自相关矩阵
P(n,n-1)= F(n,n-1)P(n-1)FH(n,n-1)+
Γ(n,n-1)Q1(n-1)ΓH(n,n-1)
(11)
步骤4:计算新息过程自相关矩阵
A(n)=C(n)P(n,n-1)CH(n)+Q2(n)
(12)
步骤5:计算滤波器增益
K(n)=P(n,n-1)CH(n)A-1(n)
(13)
步骤6:状态估计

(14)
步骤7:计算状态估计误差自相关矩阵
P(n)=[I-K(n)C(n)]P(n,n-1)
(15)
步骤8:重复以上步骤进行递推
可以看到:卡尔曼滤波的计算过程涉及矩阵求逆等复杂的操作。因此,该算法具有较大的运算量。
2.2α-β滤波
卡尔曼滤波的运算复杂度主要来自增益矩阵的求解。为了便于工程实现,出现了常增益滤波器。其中一种是α-β滤波器[7],主要针对匀速运动目标模型。其增益矩阵的表达式为

(16)
式中:α和β分别为目标状态的位置和速度分量的增益;T为采样周期。定义机动指标λ为
(17)
式中:σ1和σ2分别为过程噪声与观测噪声标准差。
滤波增益α和β的表达式为
(18)
与卡尔曼滤波类似,采用α-β滤波算法时仍然以方向余弦为观测信息,方向余弦及其变化速度为状态向量。状态转移矩阵与观测矩阵的取值也与卡尔曼滤波方法相同,分别见式(5)和式(8)。
与卡尔曼滤波相比,α-β滤波器的增益与自相关矩阵无关。因此,计算量大幅减小,易于工程实现。
2.3 自适应α-β滤波算法
自适应α-β滤波在传统α-β滤波算法的基础上,根据方差的变化来自动调节滤波增益,使误差保持在某个范围内。那么就可以避免滤波器的发散以及跟踪目标的丢失。
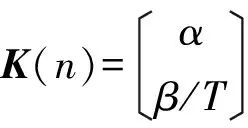
(19)
α(n)和β(n)与r的关系为
(20)
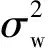
(21)
式中:a(n)为新息值;N可取3到5。
与α-β滤波算法相同,自适应α-β滤波算法仍然以方向余弦为观测信息,方向余弦及其变化速度为状态向量。状态转移矩阵与观测矩阵的取值也与卡尔曼滤波方法相同,分别见式(5)和式(8)。具体步骤与α-β滤波算法步骤相同。
3 闭环跟踪滤波算法仿真分析
3.1 野值剔除
受多种因素影响,观测数据中可能有部分数据与真实值之间存在很大误差,这些数据被称为野值。野值会对系统跟踪性能产生较大的影响,需要剔除。
采用一种基于观测向量的一步预测值的野值剔除方法。该方法的操作步骤即是将新息过程的模值与某一门限W做判决,若满足
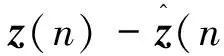
(22)
则认为观测数据有效,否则判为野值。通常门限值可选为W=3e,其中,e为观测噪声标准差。若当前观测值被判为野值,则在状态估计时利用前一周期的状态向量估计值做线性外推,即
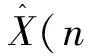
(23)
当连续3~5个观测时刻均检测到野值时判定为跟踪目标丢失。此时应当重新初始化跟踪滤波器。
3.2 坐标变换
天线测角一般以载体坐标系为参考,而跟踪滤波通常在惯性系下进行,载体姿态的变化会对跟踪滤波性能造成影响。因此,需要通过坐标变换予以克服。
将惯性坐标系原点设在载体质心上,x轴为地理上指北方向,y轴为指东方向,z轴为地平线之垂线并且指向地心的方向。设惯性坐标系下载体做匀速运动,沿x轴、y轴和z轴的速度分别为Vx、Vy和Vz,在惯性系下的三个坐标轴方向的位置分别记为X(n)、Y(n)和Z(n),n为观测时刻,观测周期为Ts,则运动方程可表示为
(24)
根据运动方程可求出目标在惯性系下归一化的方向余弦
(25)
载体坐标系原点设在载体的质心上,x轴为弹体纵轴指向运动方向,y轴为弹体纵对称面内,z轴垂直于纵对称面,右手螺旋准则确定。
弹体惯性坐标系和载体坐标系之间的转换两坐标系之间的相对关系如图4所示。

图4 载体惯性坐标系与载体坐标系示意图
载体惯性坐标系Ob-XbYbZb依次绕ObYb轴旋转α,绕ObZb轴旋转β,绕ObXb轴旋转γ。得到弹体坐标系Om-XmYmZm,载体姿态偏航角α,俯仰角β,横滚角γ, 目标在弹体坐标系Om-XmYmZm中的坐标Xm=[xm,ym,zm]。因此,从导弹惯性坐标系到导弹坐标系之间的转换关系为
(26)
其中
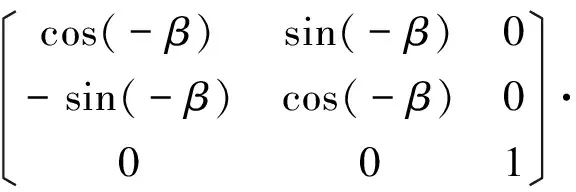
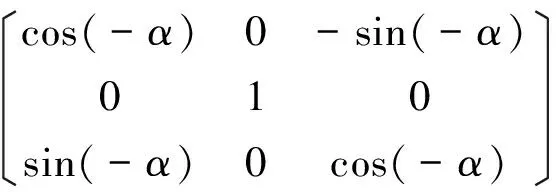
(27)
为从导弹惯性坐标系到导弹坐标系的转换矩阵。
记r1和r2分别为目标在惯性系和载体坐标系中的方向余弦,两者关系为r2=Tr1,由载体坐标系到惯性系下坐标逆变换方程为r1=T-1r2。
将惯性系下的角度转换为方向余弦,按照转换关系求出载体坐标系下的方向余弦,最后求出载体坐标系下的角度,完成角度的坐标变换。也可以将载体坐标系下的角度经过逆变换转换为惯性系下的角度。
现在考虑载体姿态的翻转,变化参数如表1所示。

表1 姿态变化参数
载体姿态如图5所示。
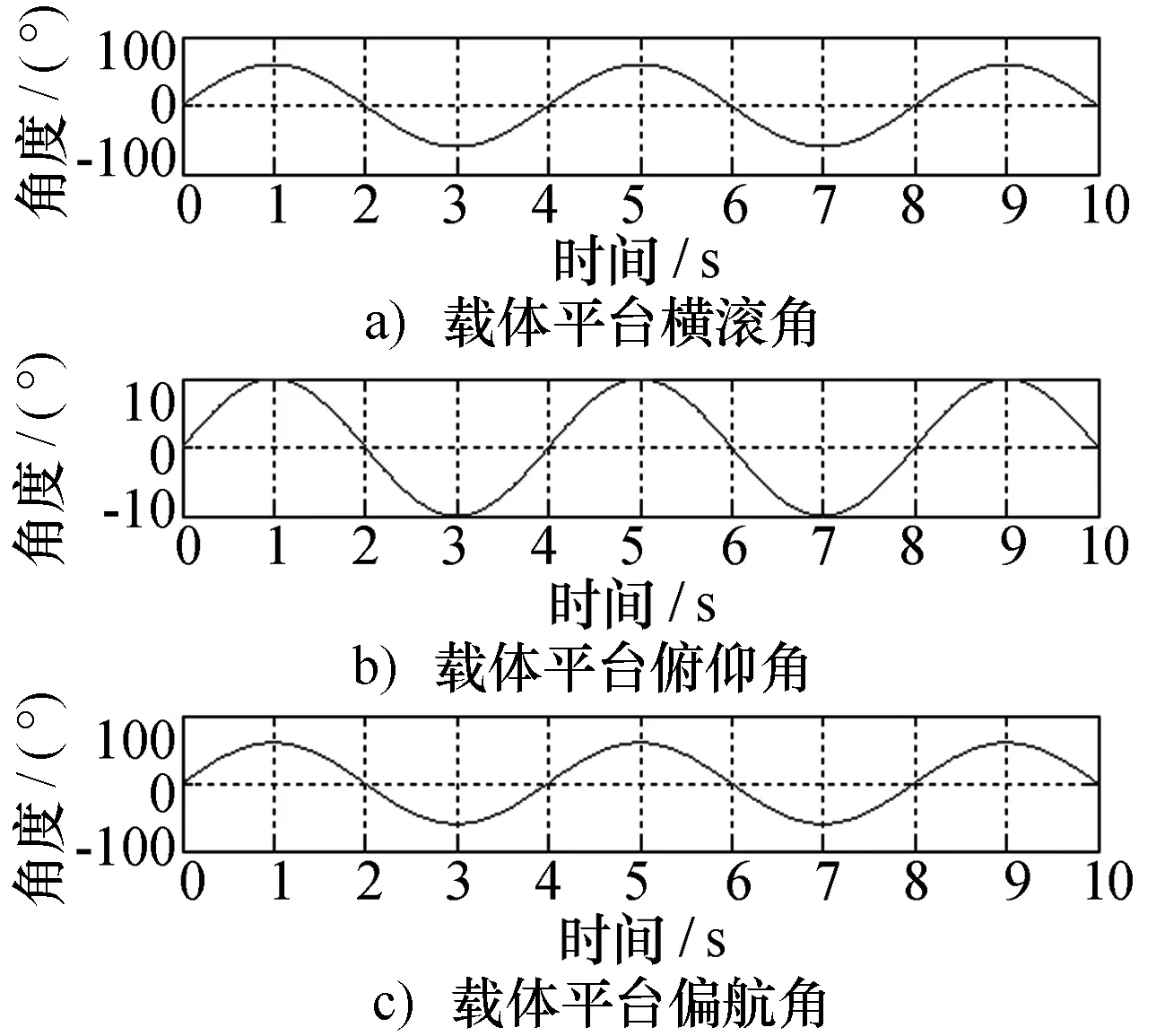
图5 载体姿态
按照坐标变换原理可得到目标载体坐标系下的方向余弦,进而求解出载体坐标系下目标信号的方位角与俯仰角。设惯性系下目标沿x轴、y轴和z轴的运动速度为100 m/s、300 m/s和500 m/s,三个坐标轴的初始位置分别为 500 km、300 km和1 000 km。图6给出了载体坐标系下目标方位角与俯仰角的变化情况。
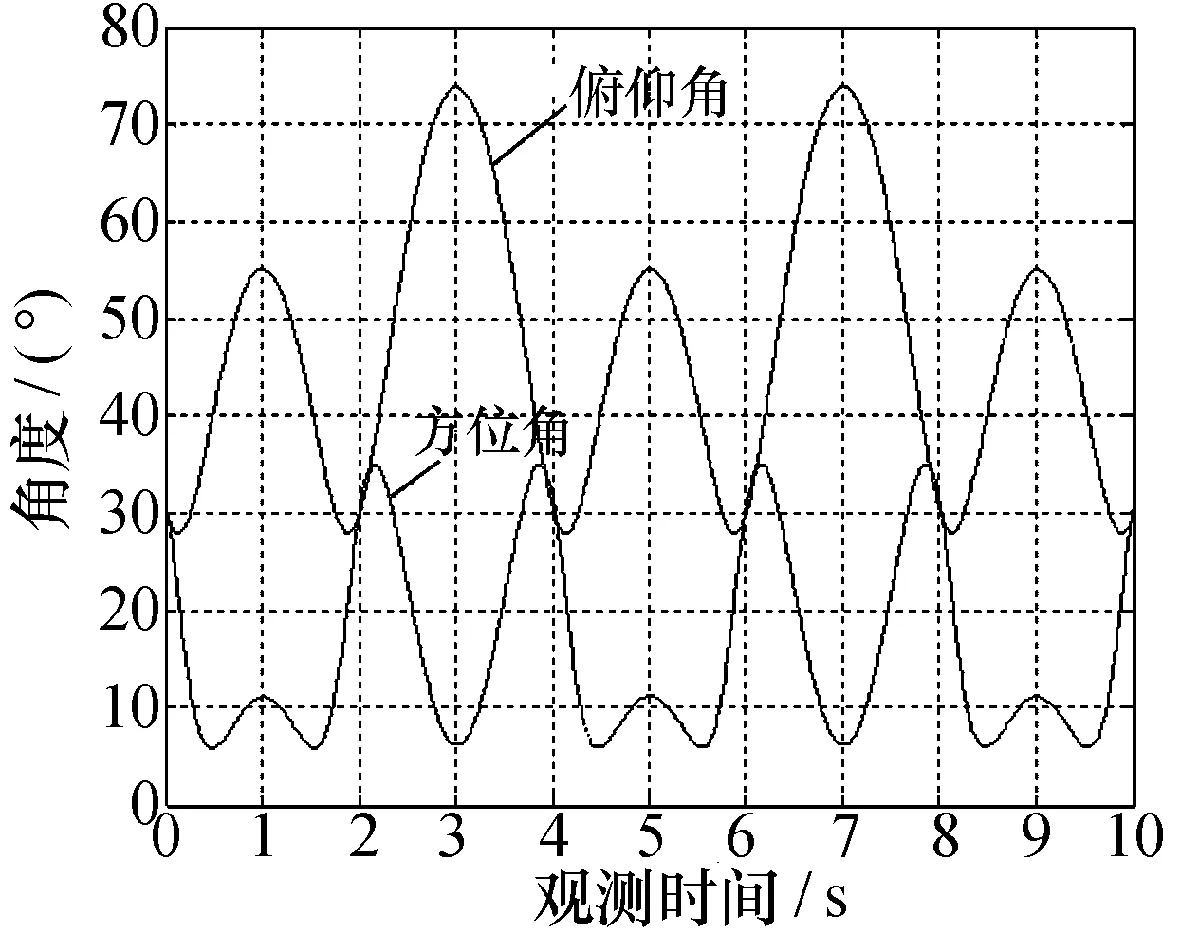
图6 载体坐标系下目标方位俯仰角变化
3.3 不同滤波算法仿真对比
为进行算法仿真对比,先建立载体运动模型,其中包含载体姿态。由运动模型可求出载体坐标系中的入射信号角度和初始波束指向。然后建模产生四个子阵输出信号并估计信号角度。角度估计结果是在载体坐标系下获得的,经过坐标逆变换可以得到惯性坐标系下的目标信号方向余弦,并以此作为观测向量进入跟踪滤波处理。跟踪滤波处理后得到惯性坐标系下的波束指向估计值,经过坐标变换转换为载体坐标系下对应的波束指向,用于下一观测时刻的信号产生和角度估计。具体跟踪滤波仿真流程如图7所示。

图7 跟踪滤波仿真流程
仿真过程数据首先根据运动模型确定目标实际的入射角和俯仰角位置,为了分析自跟踪的效果,在初始化系统过程时,进入系统角度与实际方向偏1.5个波束宽度,并基于多次独立试验得到不同观测时间测角结果和跟踪结果与实际角度之间的均方根误差(RMSE)。仿真目标状态要求跟踪过程要趋于收敛且整体的误差小于0.5°,在实现过程中每隔2 ms更新一次角度结果。
结合上一节的运动模型,对三种跟踪滤波算法性能进行仿真对比。仿真时不考虑幅相误差等非理想因素,信噪比设置为-10 dB。图8、图9给出了仿真结果。
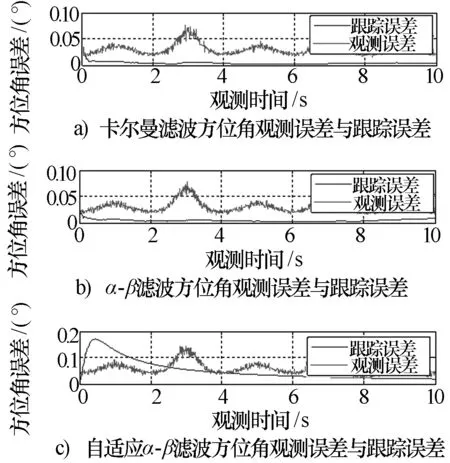
图8 不同跟踪算法方位角观测误差与跟踪误差
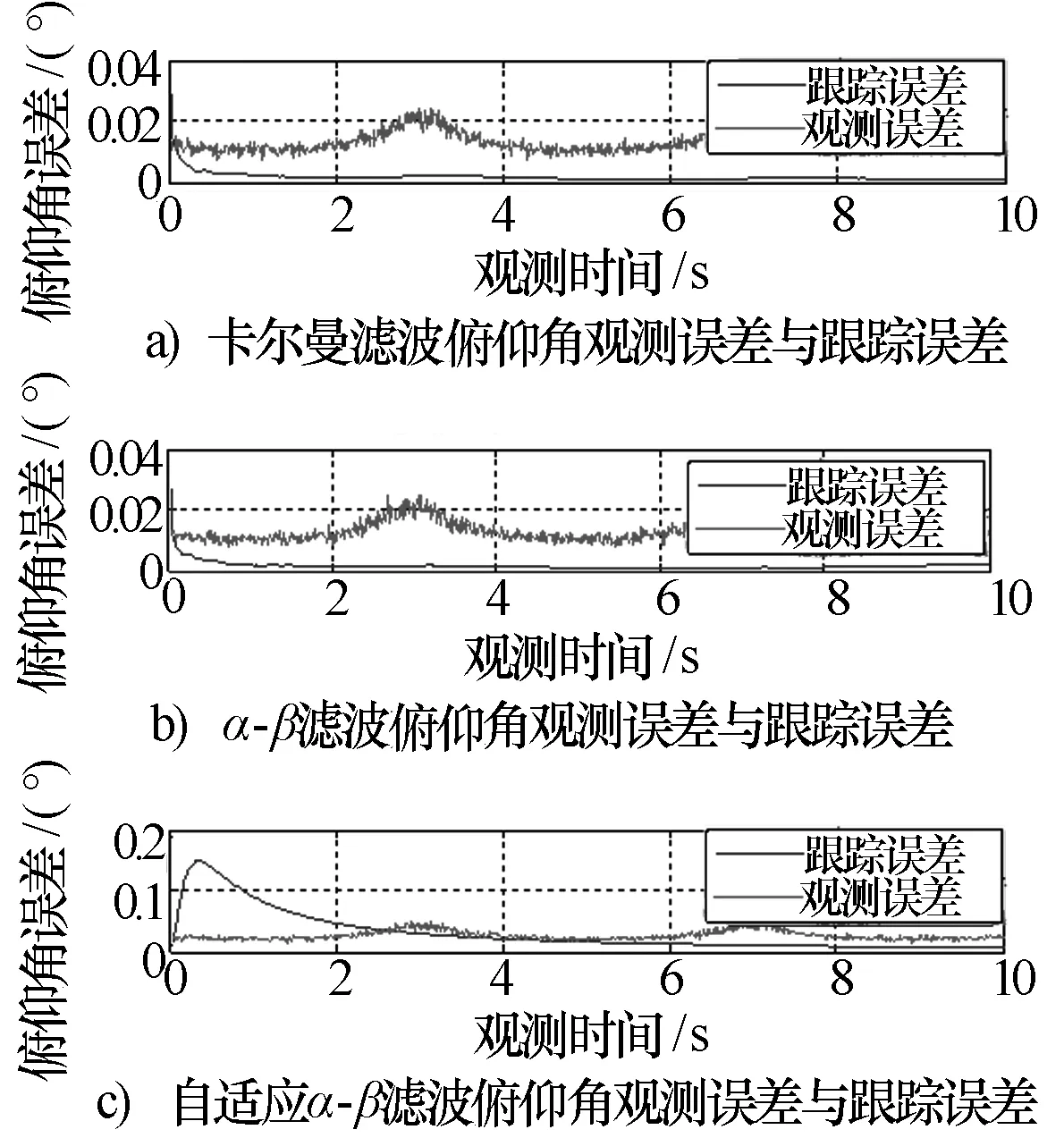
图9 不同跟踪算法俯仰角观测误差与跟踪误差
比较三种跟踪方法可以看到:跟踪误差随着观测时间的增大均小于观测误差,说明滤波过程有效地提高了跟踪精度。卡尔曼滤波算法和α-β滤波算法得到的测角和跟踪误差接近。两种方法的跟踪误差大约为测角误差的1/5以下,有较好的跟踪效果。图中可以直观地看出从跟踪误差这个方面进行比较,传统α-β滤波算法收敛较快,自适应α-β算法收敛相对较慢,而自适应α-β算法在稳定之后曲线更为平滑,更稳定。
根据三种方法的原理,卡尔曼滤波需要实时计算增益矩阵。增益矩阵的计算涉及一步预测自相关和新息过程自相关矩阵的估计以及矩阵求逆过程,计算量大。自适应α-β算法虽然收敛后曲线更平滑,但收敛速度较慢,难以适应快速的载机姿态变化。此外,在实际运用中,自适应α-β滤波算法需要实时的量测噪声精度,而我们面阵的量测噪声精度与入射角是时变的,难以实时给出。因此,经过综合考虑,我们方案中选用的跟踪滤波算法为传统α-β滤波算法,其更适合本系统的处理方法。
3.4 不同场景下α-β滤波算法性能仿真
根据上一节的讨论,α-β滤波算法更适合工程实现。基于建立的运动模型,通过仿真讨论信噪比、波束指向误差以及载体姿态测量误差对系统α-β滤波算法性能造成的影响。
3.4.1 信噪比对α-β滤波性能影响
考虑信噪比的影响。设置三种不同大小的信噪比场景,分别为-20 dB、-10 dB、0 dB。图10和图11分别给出了不同信噪比下,方位与俯仰角的测角与跟踪误差的对比情况。

图10 不同信噪比下的方位角测角和跟踪误差曲线
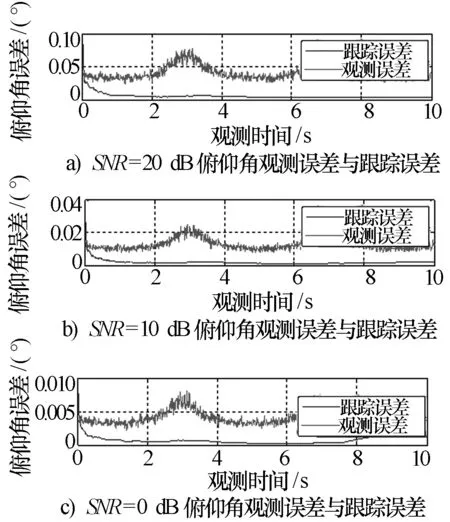
图11 不同信噪比下的俯仰角测角和跟踪误差曲线
由图10和图11可知,随着信噪比降低,测角和跟踪误差增大。测角误差曲线仍然存在较大的波动,目标角度值较大处测角误差明显增大。跟踪误差曲线则相对平滑,波动情况得到改善。三种场景下,经过1 s的时间跟踪误差曲线基本收敛,此时可认为进入稳定跟踪状态。随着信噪比增加,跟踪误差减小。
3.4.2 波束指向误差对α-β滤波性能影响
波束指向误差,是指阵列天线波束指向的理想值与真实指向之间的偏差。波束指向误差受多种因素影响,如:阵元及射频通道的幅相不一致性及移相器的相位量化误差等。设置了三种不同大小的波束指向误差,观察测角误差和跟踪误差曲线的变化情况。信噪比均为-10 dB,波束指向误差按照高斯分布建模,误差参数依次为方差为0°、1°、2°。
不同波束指向误差下的测角和跟踪误差仿真结果见图12、图13。可以看到:波束指向误差增大时,测角和跟踪误差均明显增大。因此,波束指向误差对测角和跟踪滤波的性能均有较大的影响。测角误差曲线仍然随着信号角度的改变有较大的起伏波动。
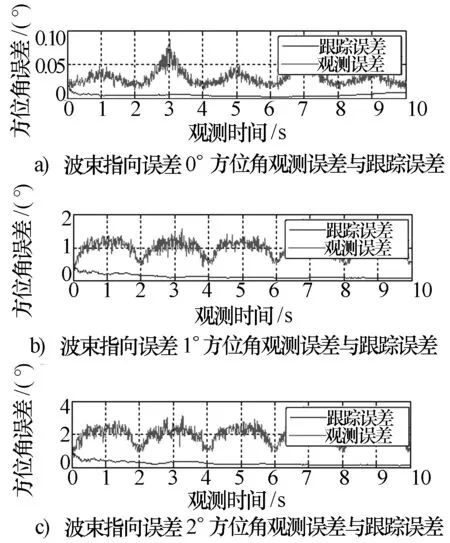
图12 不同波束指向误差下的方位角测角和跟踪误差曲线
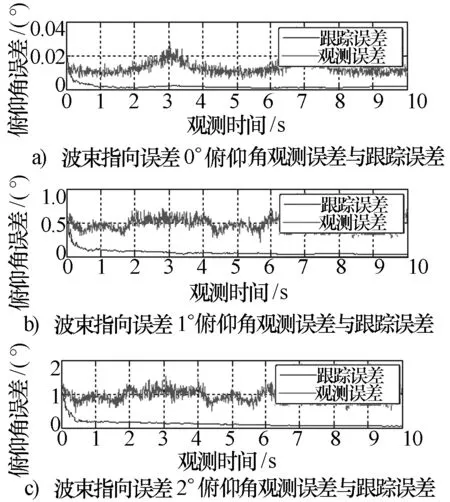
图13 不同波束指向误差下的俯仰测角和跟踪误差曲线
3.4.3 载体姿态测量误差对α-β滤波性能影响
α-β跟踪滤波算法处理过程中,坐标变换与逆变换将用到载体姿态信息。实际工程中,载体姿态测量存在误差,会对测角和跟踪滤波性能造成影响。
载体姿态测量误差以高斯分布建模,通过改变其方差来改变测量误差大小。不同的载体姿态测量误差下的测角和跟踪误差对比情况见图14和图15。三种场景下信噪比均为-10 dB。姿态测量误差的参数依次为方差为1°、2°、3°。

图14 不同姿态测量误差下的方位角测角和跟踪误差曲线
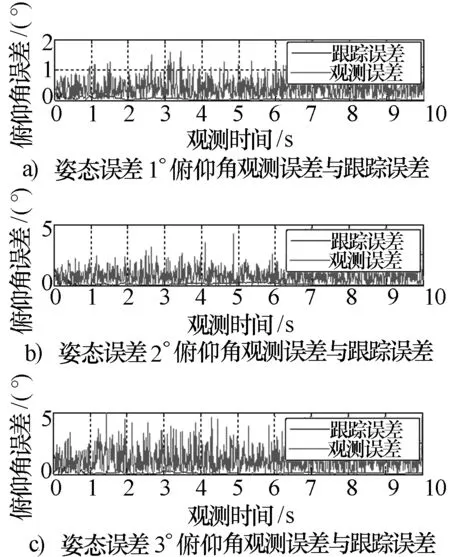
图15 不同姿态测量误差下的俯仰角测角和跟踪误差曲线
从图14和图15可以看到:当载体姿态测量误差增大时,测角误差和跟踪误差显著增大,说明载体姿态测量误差对测角和跟踪精度影响很大。考虑载体姿态误差时,测角误差曲线随信号角度变化的起伏不明显,说明此时入射信号角度大小已经是影响测角的次要因素。
综合考虑,在本节考虑的非理想因素中载体姿态测量误差是对测角和跟踪性能影响最大的因素。
4 结束语
本文针对高速运动平台上相控阵卫星自跟踪系统闭环跟踪滤波,介绍了系统的总体流程,二维测角方法,卡尔曼滤波、α-β滤波以及自适应α-β滤波算法的基本原理,以及坐标变换与逆变换和野值剔除的方法。随后建立相应的运动场景,对三种跟踪滤波算法的性能做了对比,选择α-β滤波作为系统跟踪滤波的处理方法。研究了不同场景下的α-β滤波算法性能。研究过程中主要讨论了信噪比、幅相误差、波束指向误差以及载体姿态测量误差对测角和跟踪滤波算法性能的影响。
[1] GUESALAGA A,TEPPER S.Synthesis of automatic gain controllers for conical scan tracking radar[J].IEEE Transactions and Electronic Systems, Aerospace and Electronic Systems, 2000, 36(1):302-309.
[2] 牛宝君, 李延波. 二维相控阵单脉冲跟踪测角方法的研究与应用[J]. 现代雷达, 2003, 25(5): 16-18. NIU Baojun, LI Yanbo. Study and application of angle measurement for 2-D phased array monopulse tracking[J]. Modern Radar, 2003, 25(5): 16-18.
[3] 韩彦明, 陈希信. 自适应和差波束形成与单脉冲测角研究[J]. 现代雷达, 2010, 32(12): 44-47. HAN Yanming, CHEN Xixin. A study on adaptive sum and difference beam forming and monopulse angle estimation[J]. Modern Radar, 2010, 32(12): 44-47.
[4] 陈知明, 魏述刚. 相控阵雷达测角误差自适应计算方法[J]. 现代雷达, 2013, 35(7): 13-15. CHEN Zhiming, WEI Shugang. Self-adaptive calculation method of angle error curve measurement for phased array antenna[J]. Modern Radar, 2013, 35(7): 13-15.
[5] 李朝海, 姜雯献, 王国龙,等. 弹载相控阵卫星跟踪系统设计与测角研究[J]. 现代雷达, 2014, 36(11): 18-23. LI Chaohai, JIANG Wenxian, WANG Guolong, et al. Design of satellite tracking system for missile-borne phased array radar and study on angle measurement[J]. Modern Radar, 2014, 36(11): 18-23.
[6] SHARMA S, DESHPANDE S, SIVALINGAM K M. Alpha-beta filter based target tracking in clustered wireless sensor networks[C]// 2011 Third International Conference on Communication Systems and Networks (COMSNETS). Bangalore: IEEE Press, 2011: 1-4.
[7] CHIOU Y S, WANG C L, YEH S C. Reduced-complexity scheme using alpha-beta filtering for location tracking[J]. Communications, IET, 2011, 5(13): 1806-1813.
向晓萍 女,1991年生,硕士研究生。研究方向为阵列雷达信号处理。
李朝海 男,1972年生,高级工程师。研究方向为高速实时信号处理、雷达系统及信号处理。
黄宇声 男,1989年生,硕士研究生。研究方向为阵列信号处理。
A Study on the Closed-loop Tracking Filtering of Phased Array Satellite Tracking System
XIANG Xiaoping,HUANG Yusheng,LI Chaohai
(School of Electronic Engineering,University of Electronic Science and Technology of China, Chengdu 611731, China)
In order to realize the same direction between the beam pointing of phased array antenna on the high-speed motion platform and the satellite,the overall frame and main signal processing procedures of the phased array satellite tracking system are presented in this paper. The closed-loop tracking filter which includes the steps of angle estimation and tracking filtering is the core processing module of satellite tracking system. The phase-comparison angle measurement algorithm of two dimensional array is used to get the estimated value of the angles and the angles are the input parameters of the tracking filtering process. The result of the tracking filtering is returned to the angle measurement algorithm to form a closed loop tracking. The Kalman filter,α-βfilter and adaptiveα-βfilter algorithm are researched. The method of coordinate transformation and outlier removal are given. The tracking accuracy of different tracking filter algorithms is completed through simulation, and the algorithm performance ofα-βfilter is analyzed under different scenarios. The simulation results show that the tracking accuracy of theα-βfilter is high, which can be applied to the high-speed mobile tracking system.
phased array; satellite tracking; angle measurement; tracking filtering
10.16592/ j.cnki.1004-7859.2016.03.012
国家自然科学基金资助项目(61101173);中央高校基本科研业务费(ZYGX20100020)
向晓萍 Email:xxpllg123@163.com
2015-10-18
2015-12-20
TN974
A
1004-7859(2016)03-0054-07
