基于检测性能的隐身目标探测研究
2016-12-20童创明李西敏王义哲
陈 彬,童创明,李西敏,王义哲
(空军工程大学 防空反导学院, 西安 710051)
·总体工程·
基于检测性能的隐身目标探测研究
陈 彬,童创明,李西敏,王义哲
(空军工程大学 防空反导学院, 西安 710051)
针对单基地雷达难以有效探测隐身目标的问题,提出了一种基于雷达网检测性能的隐身目标探测方法。在推导雷达距离方程的基础上,结合Swerling1起伏目标模型和区域剖分方法,计算并分析了单/双站雷达对隐身目标的探测区域;然后,采用物理光学和等效电磁流法,仿真分析了结构隐身目标的单/双站雷达散射截面积,并结合典型布站方式,分别解算出等边三角形、正方形、蜂窝形三种布站方式下,单基地组网雷达和复合式组网雷达对隐身目标的探测能力和布站效率,从而甄选出最优雷达布站方式和组网模式;最后,理论分析与仿真结果验证了优化雷达组网布站的应用性和可行性。
隐身目标;检测性能;雷达网;探测范围
0 引 言
为了对抗现代战争中敌方雷达的探测,隐身飞机成为世界各大强国军事发展的重点。飞行器隐身技术的应用,使得单部雷达难以实现对其探测与跟踪,只能得到断续的航迹,预警距离也大大缩减。当前,隐身技术主要有结构隐身和吸波材料隐身,其中前者占主要因素。结构隐身是通过结构设计,将电磁波散射到对其威胁较小的方向上,该设计主要集中在正前鼻锥方向水平±45°,其他方向雷达散射截面(RCS)变化不大,有些方向甚至被加强。因此,通过雷达组网可实现对隐身目标的探测与跟踪,特别是在目前尚无单部雷达具备对隐身目标探测跟踪能力的条件下,对抗隐身目标较有效的方法就是雷达组网。
针对隐身目标的探测,许多专家学者展开了研究。文献[1]基于临近空间作战平台进行研究;文献[2]基于最小可检测信号,采用网格剖分法研究隐身目标的探测;文献[3-5]基于RCS的经验公式,分析了组网雷达对隐身目标的探测。针对隐身目标的探测,既要充分认识到其RCS随角度剧烈起伏,不能用经验公式统而代之,又要尽量保证设定的参数合理适度,仿真的方法精确、高效。因此,本文以A型飞机作为典型结构隐身目标,以该型飞机全金属几何模型为基础,提出了一种基于检测性能的探测方法,计算单、双站雷达在满足一定检测性能(以检测概率和预警概率表征)下对隐身目标的探测范围,探究组网雷达对结构隐身目标的探测能力。为真实反映隐身目标RCS起伏,应用物理光学和等效电磁流方法,计算该型飞机金属模型在不同入射角下的单/双站RCS,并结合典型的布站方式,仿真分析了复合式组网雷达在不同布站方式下的探测范围和布站效率,验证了优化雷达组网布站的应用性和可行性。
1 单/双基地雷达探测范围分析
1.1 单/双基地雷达探测范围剖分
随着探测目标位置的变换,目标的散射截面积σ会发生变化,雷达接收到的回波信号强度也在时刻发生变化,可探测区域因此是无规律性的,而网格剖分法可以有效地计算雷达的探测范围[4]。
假定目标在某一高度,作水平直线飞行。首先,设定以单基地雷达或双基地雷达基线中心为原点的水平面为警戒区域,以目标飞行方向的反方向为y轴正方向,水平面内与y轴垂直方向为x轴;然后,对这个区域沿x、y轴进行网格剖分,剖分步长为Δx、Δy;最后,用第i行、第j列的节点坐标(i,j)表示目标位置。剖分步长Δx、Δy越小,结果越精确,但是计算量也越大,因此要选定合适的步长。
若不考虑系统损耗因子和大气衰减因子,根据简单点目标的单基地雷达距离方程,某型S波段雷达的作用距离可表示为
(1)
式中:PT为发射机发射功率;G为雷达天线的增益;σ为目标的雷达散射截面;k为玻尔兹曼常数;T0为标准室温;Bn为噪声宽带;Fn为噪声系数;(SNR)omin为满足所需检测性能(以检测概率和预警概率表征)时,接收机匹配滤波器的最小输出信号噪声功率比。
若不考虑系统损耗因子和大气衰减因子,根据简单点目标的双基地雷达距离方程,某型S波段雷达的作用距离可表示为
(2)
式中:RT、RR分别为目标与发射站、接收站之间的距离;GT、GR分别为发射、接受天线的增益;σβ为目标的双站雷达散射截面。
1.2 单/双基地雷达最大探测距离的计算
大部分公开文献都是直接给定雷达的最小可检测信噪比,但是SNR是在满足一定检测性能(以检测概率和预警概率表征)时的信噪比。在不同检测性能下,雷达的SNR是不同的,因此脱离检测性能探讨SNR是没有意义的。又因为隐身目标的RCS随方位角变化而剧烈起伏,为准确表示检测概率与SNR的关系,在此引入Swerling1起伏目标模型[6]。
在Pfa=10-6时,根据图1可由目标的发现概率换算出所需的信噪比SNR。

图1 Pfd=10-6时,Swerling1型目标模型
文献[7]给出了求取雷达发现概率的近似表达式,目标的检测概率Pd可表示为
(3)
(4)
式中:S为信号功率;N为噪声功率;b为发现门限电压值;n为积累脉冲数。
设同一目标在不同距离上的回波信号功率分别为S1和S2。对同一参数的雷达、相同的环境下,则有
(5)
若雷达参数确定、背景环境不变,雷达方程可以由式(1)简化为
(6)
式中:K为雷达威力系数。
假设该雷达在虚警概率Pfa=10-6,发现概率Pd=0.8时,对雷达散射截面σm目标的探测距离为Rm,则联立式(5)、式(6),可得该雷达发现概率
(7)

同理,可推导出双基地雷达发现概率的近似表达式
(8)
式中:RT、RR分别为目标与发射站、接收站之间的距离;σβ为目标的双站雷达散射截面。
因此,可求得在任意位置(i,j)处目标的发现概率Pd(i,j),再由图(1)换算该发现概率下所需的信噪比(SNR)Pd(i,j),因此,可以得出雷达对该目标在发现概率为Pd0(Pd0≠Pd(i,j))时的最大探测距离为[8]
(9)
式中:R(i,j)为节点(i,j)与雷达之间的距离;(SNR)Pd(i,j)和(SNR)Pd0分别是发现概率为Pd(i,j)和Pd0时所需的信噪比。
2 隐身目标单/双站RCS计算
2.1 RCS计算方法
本文以A型飞机作为典型的结构隐身目标,采用PO+MEC混合法计算S波段该型飞机的单、双站RCS特性。
物理光学法(PO)出发点是Stratton-Chu散射场积分方程,用散射体表面的感应电流作为散射源,然后对其积分而求得散射场。在平面波入射情况下,物体表面远区散射场可写为
(10)


图2 目标表面电磁散射示意图
等效电磁流法[9](MEC)则是对棱边的绕射计算:对边缘为C的任意劈边,表示它的远区边缘绕射场为
(11)
2.2 隐身目标单站RCS特性
根据图3可以看出,该算法计算结果与商用软件计算结果吻合较好,验证了该算法的正确性。从图3中可以看出,随入射角变化,该型飞机的RCS值起伏较大,最大值和最小值之差约为40 dB,而且在正前鼻锥方向(入射角为0°)水平±30°和正后方(入射角为180°)±30°范围内RCS值较小,其平均值分别为-9 dB和-7 dB,隐身效果明显,但其侧向RCS较大。
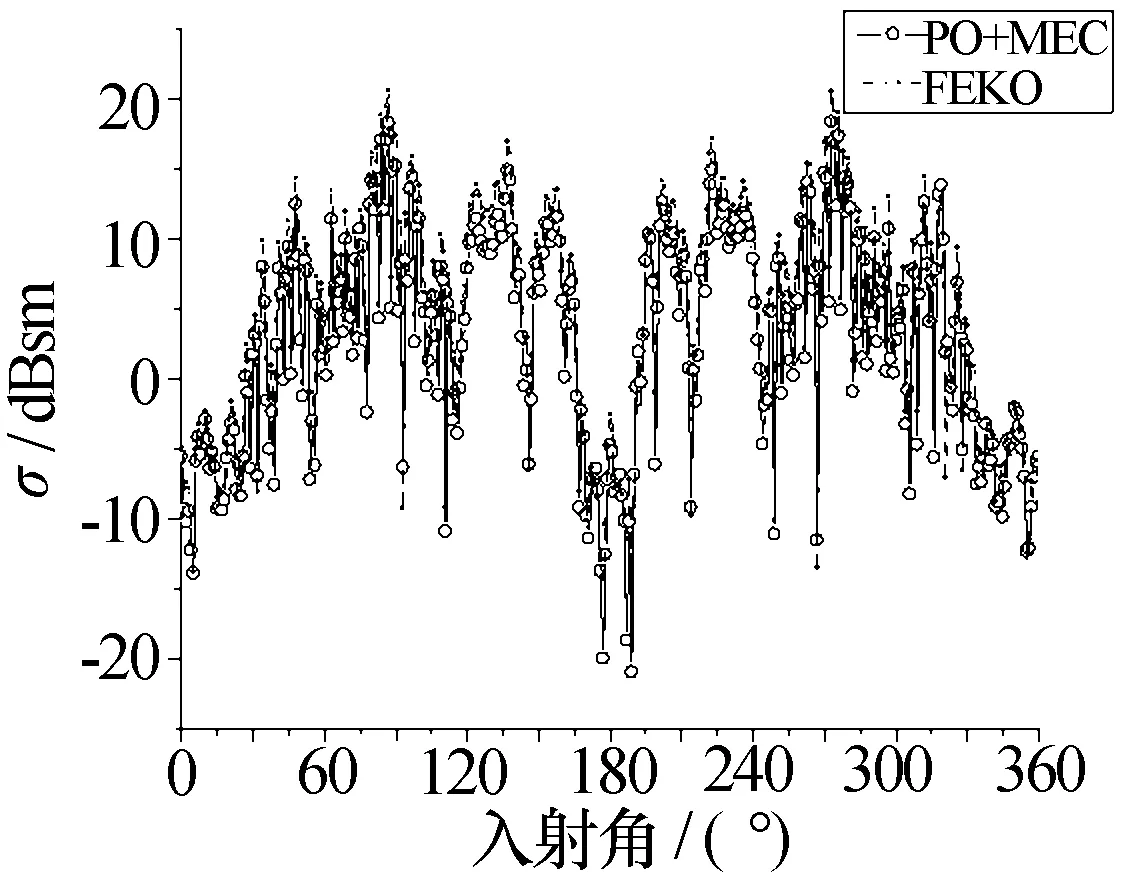
图3 f=3 GHz时A型飞机的单站RCS特性曲线
2.3 隐身目标双站RCS特性
从图4可以看出,在入射角一定的情况下,随着接收角的变化,RCS也剧烈变化;当从侧向入射(入射角为90°和270°)、前向散射接收(接收角为270°和90°)时,RCS取值较大。因此,在隐身飞机临近双基地雷达的过程中,随着前向散射增强,雷达接收站接收的目标回波信号强度逐渐增大,接收站对目标的跟踪能力也随之增强。
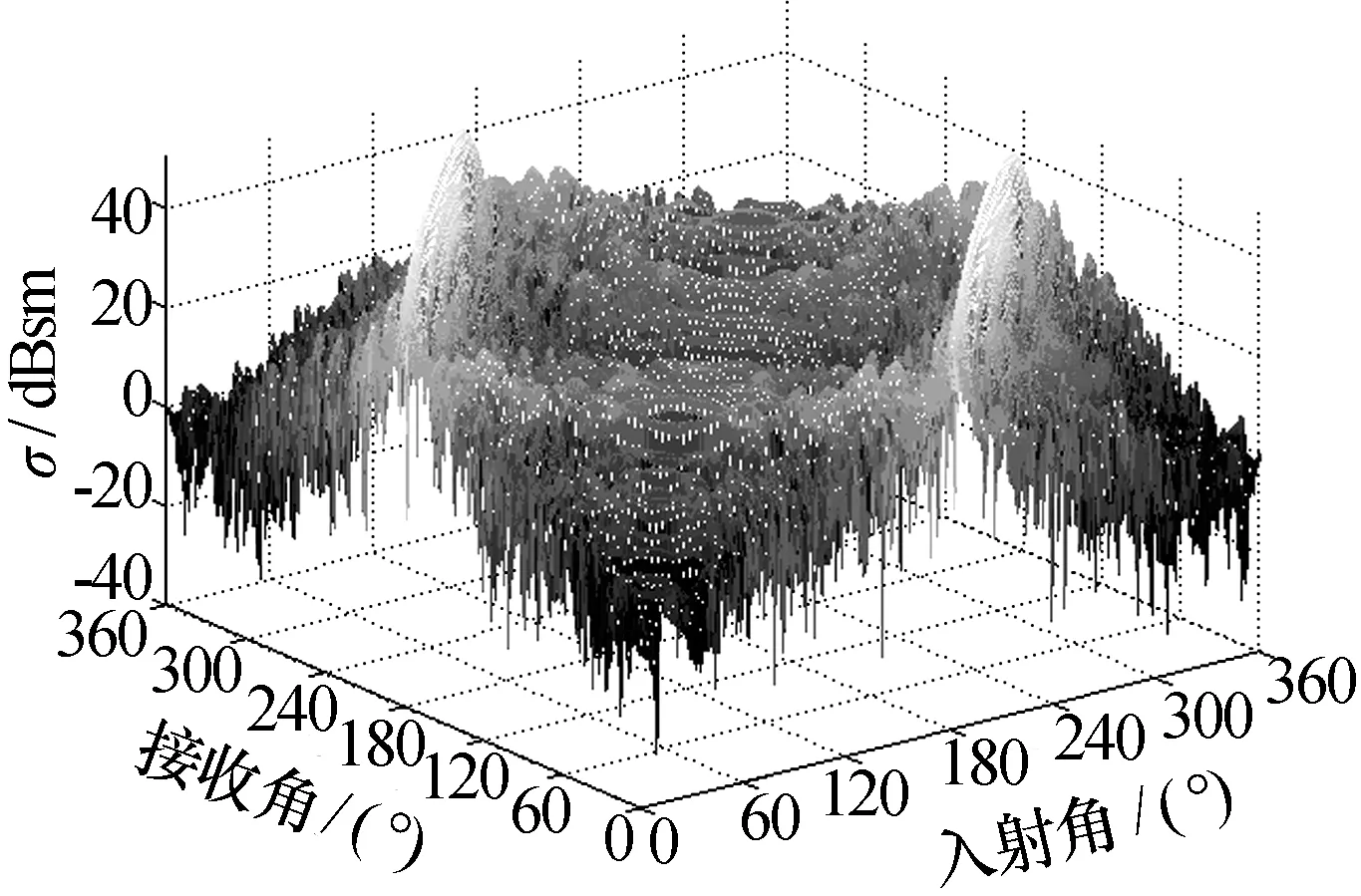
图4 f=3 GHz时A型飞机的双站RCS特性曲线
3 雷达网布站方式的分析与仿真
3.1 雷达网布站方式的分析
定义警戒雷达组网的布站效率:探测区域与所花费代价的比值,可表示为
(12)
式中:η为雷达组网布站效率;S为雷达网探测区域;C为花费的代价。
由于使用相同威力范围的雷达组网,有
C(1)=…=C(N)=C0
(13)
所以雷达组网的总花费代价为C=N×C0。其中,C0为单个雷达花费代价,N是组网雷达的个数。因此当组网的雷达确定后,组网所花费的代价与组网使用的雷达数量N是等价的。
为便于比较,定义归一化布站效率:雷达组网的布站效率与单基地的效率的比值,可表示为
(14)
对于同一散射截面的探测,在方位上的对称性是雷达探测的重要特点。因此,雷达组网布站要从对称性入手,将雷达布置成对称性好的几何图形将保证较高的目标探测发现能力。另外,只有满足顶角除360是一个大于3的整数的完全对称(边长和顶角相等)多边形,才能不留有任何空隙的填充一个平面。满足上述条件的完全对称的规则多边形只有等边三角形、正方形和等边六边形三种排布方式。
3.2 雷达探测范围的仿真
设定单基地雷达发射功率PT=1 000 kW;雷达天线的增益G=33 dB;玻尔兹曼常数k=1.38×10-23J/k;标准室温T0一般取290 K;噪声宽带Bn=106Hz;噪声系数Fn=1.5 dB;虚警概率Pfa=10-6。采用上述方法分别计算该单基地雷达在满足发现概率Pd=0.6、Pd=0.7和Pd=0.8的指标时,对A型飞机的探测区域,结果如图5所示,图中黑影部分为可探测区域,空白部分为不可探测区域。
由图5可知,随着发现概率指标的提高,雷达对目标的可探测区域逐渐减小。且在三种发现概率下,该单基地雷达对A型飞机的探测能力在正前鼻锥方向水平±30°范围内都急剧缩减,其他方向上探测区域存在不同程度离散,影响对目标的稳定跟踪。为提高对隐身目标前向探测能力,延长预警距离,稳定跟踪目标,下面采用双基地雷达组网技术进行仿真分析。
设定发现概率指标Pd=0.8;发射、接受天线的增益GT=33 dB、GR=33 dB,其他假定条件不变,双基雷达采用左发右收,则不同基线距离下对战机A的探测范围如图6所示。
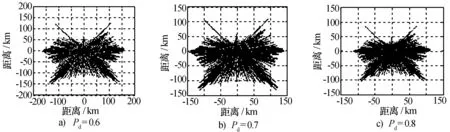
图5 单基地雷达探测范围
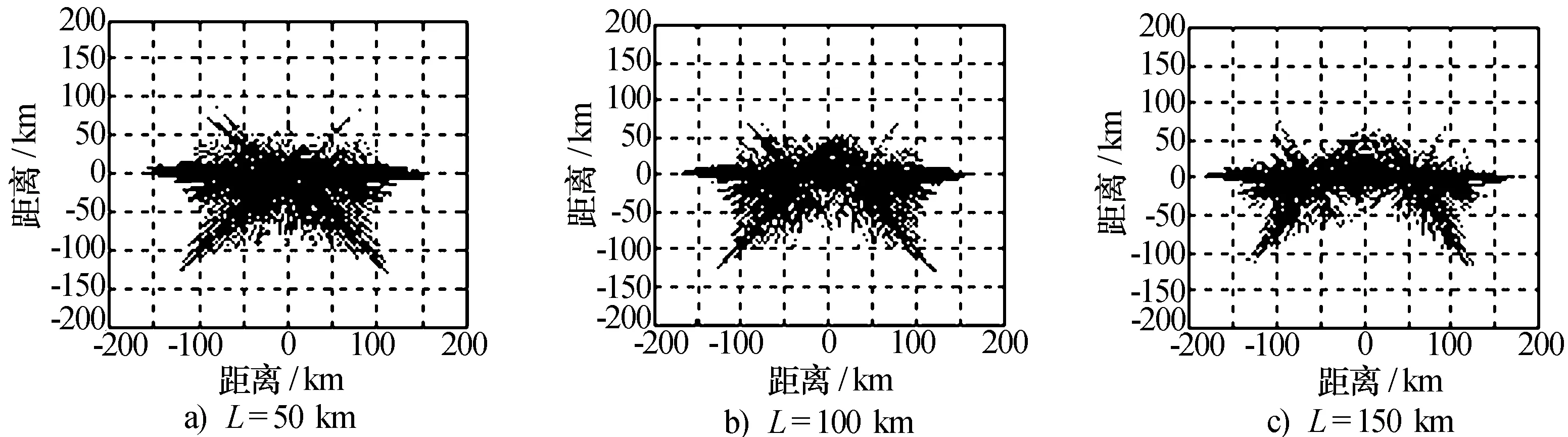
图6 Pd=0.8时双基地雷达探测范围
从图6中可以看出,当基线距离L=50 km时,双基雷达探测区域与单基轮廓相近,前向探测距离无明显加强,这是因为收发站较近时,近似于单基雷达;当基线距离L=100 km时,双基雷达前向探测能力有较明显加强,但后向探测能力略有削弱;当基线距离L=150 km时,前向探测区域离散,影响稳定跟踪,后向探测能力削弱。因此,选定双基雷达基线距离L=100 km。
下面对等边三角形、正方形和六边形三种布站方式进行仿真,计算三种布站方式组网效率。为方便比较,选定相同参数雷达分别进行单基地组网和复合组网:复合组网模式下,组网雷达间距为选定的基线距离,收、发站交替布站;单基地组网模式下,组网雷达独立工作,布站位置与复合组网一致。
3.3 仿真结果分析
对于三种不同的布站方式,在设定发现概率Pd=0.8,双基雷达基线距离L=100 km的前提下,比较图7、图8可得以下结论:
(1)等边三角形布站方式下,单基地组网模式时,探测区域内部局部离散,影响对目标的稳定跟踪;复合组网模式下,探测区域内部连续,可在全方位上完成对要地中心的预警探测和对目标的稳定跟踪任务。
(2)正方形布站方式下,单基地组网模式时,探测区域内部存在较大盲区,无法完成预警探测任务;复合组网模式时,探测区域内部存在盲区,在一定程度上影响对目标的探测与跟踪。
(3)蜂窝形布站方式下,单基地组网模式时,探测区域内部存在盲区,且离散区域较大,影响对目标的预警探测;复合组网模式下,探测区域内部局部离散,对目标的稳定跟踪略有影响。
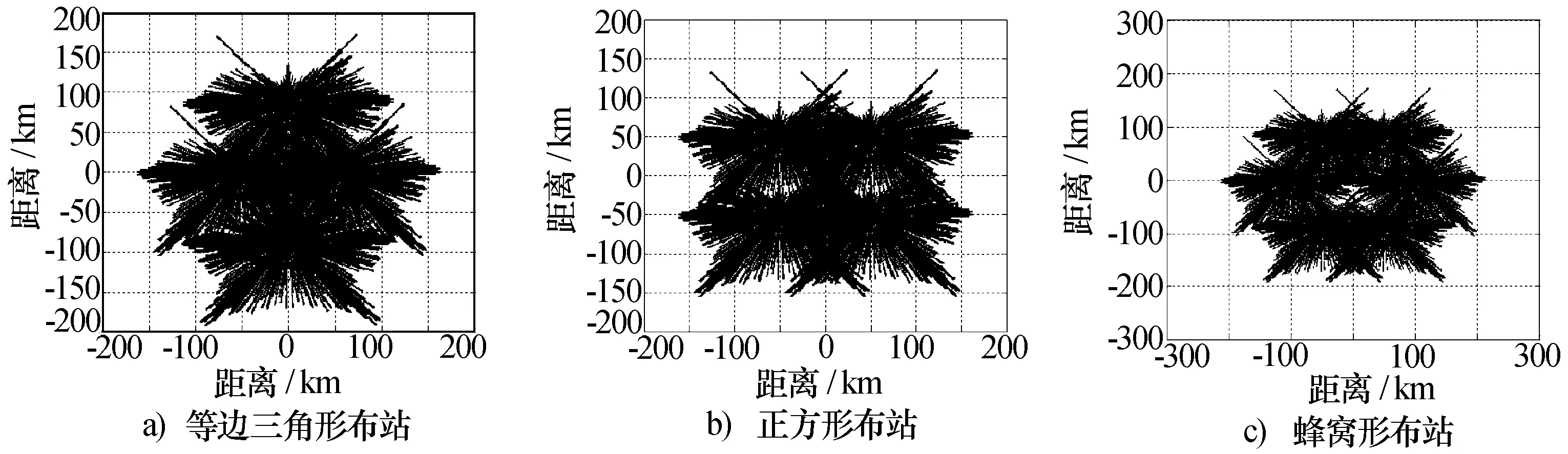
图7 Pd=0.8时单基地组网探测范围

图8 Pd=0.8时复合组网探测范围
下面从最大探测范围和归一化布站效率两个方面衡量组网布站探测效能,三种布站方式的比较见表1。

表1 三种布站方式探测效能
综上所述,同等参数雷达,通过组网均可增强对目标的前向探测能力;组网的布站效率以正方形布站方式最优、等边三角形稍次、蜂窝形最次;复合式雷达组网在预警探测、稳定跟踪隐身目标方面性能明显优于单基地雷达组网。因此,选择复合式等边三角形布站可以获得较好的前向探测能力和较大的稳定跟踪区域,而复合式正方形布站可以获得较大的前向探测区域和最优的布站效率。
4 结束语
对于隐身飞机目标,由于其在正前方(入射角为0°)和正后方(入射角为180°)±30°范围内RCS值均较小,隐身效果明显,导致单基地雷达对其的探测能力大幅下降,而雷达组网可利用结构隐身目标侧向RCS较大,隐身效果大大降低的特点,完成对其的预警探测任务。本文提出了一种基于检测性能的结构隐身目标探测范围计算方法;仿真并分析了等边三角形、正方形、蜂窝形布站方式下单基地组网和复合式组网后对隐身目标的探测能力和布站效率。结果表明,通过合理的选择布站方式和组网模式,可以提升对隐身目标的探测能力。利用单基地雷达组网布站,可以有多种工作模式和组合方式,若使雷达交替收发,并合理选择基线距离和组网布站搭配方式,理论上可以进一步提高雷达网对隐身目标的探测能力,获得更高的布站效率,这是下一步工作的重点。
[1] 门向生,田新华,宫 健. 临近空间双基雷达探测隐身目标性能研究[J]. 电光与控制,2009, 16(5): 43-46. MEN Xiangsheng, TIAN Xinhua, GONG Jian. Study on the capability of near space bistatic radar in detecting stealth targets[J]. Electronics Optics & Control, 2009, 16(5): 43-46.
[2] 吴小坡,时家明,莫正攀,等. 双基地雷达对隐身目标探测区域的计算[J]. 现代防御技术,2012, 40(4): 123-127. WU Xiaopo, SHI Jiaming, MO Zhengpan, et al. Calculation of detection coverage of bistatic radar against stealth target[J]. Modern Defence Technology, 2012, 40(4): 123-127.
[3] 任爱众,张正勇,贾海涛,等. 组网融合探测隐身目标的效能分析[J]. 现代雷达,2013, 36(10): 1-4,8. REN Aizhong, ZHANG Zhengyong, JIA Haitao, et al. Efficiency analysis for detecting stealth target by netted radar[J]. Modern Radar, 2013, 36(10): 1-4,8.
[4] 张新勋,张 兵,皇甫流成, 等. 复合式双基地雷达网反隐身性能研究[J]. 火力与指挥控制,2014, 39(3): 414-420. ZHANG Xinxun, ZHANG Bing, HUANGFU Liucheng, et al. Study on anti-stealth capability of complex bi-static radar net[J]. Fire Control & Command Control, 2014, 39(3): 414-420.
[5] 张华涛.多频段雷达组网探测跟踪隐身目标研究[J]. 现代电子技术,2014, 37(7): 46-49. ZHANG Huatao. Research on multi-band radar networking detecting and tracking of maneuvering stealthy target[J]. Modern Electronics Technique, 2014, 37(7): 46-49.
[6] CUI G,DEMAIO A,PIEZZO M. Performance prediction of the incoherent radar dector for correlated generalized swerling-chi fluctuating targets[J]. IEEE Transactions on AES,2013, 49(1): 356-368.
[7] 戴 筠. 雷达组网反隐身技术可行性探讨[J]. 现代雷达,1998, 19(3): 8-13. DAI Jun. An investigation of feasibility of anti-steal techniques for radar networks[J]. Modern Radar, 1998, 19(3): 8-13.
[8] 杨龙坡,熊家军. 基于实测数据的雷达探测距离修正方法[J]. 现代防御技术,2011, 39(3): 139-142. YANG Longpo, XIONG Jiajun. A method of correcting the detection range of radar based on detected data[J]. Modern Defence Technology, 2011, 39(3): 139-142.
[9] MICHAELI A. Equivalent edge currents for arbitrary aspects of observation[J]. IEEE Trans. Antennas Propagat, 1984, 32(3): 252-258.
陈 彬 男,1992年生,硕士。研究方向为目标电磁散射特性。
A Study on the Stealth Target Detection Based on the Detection Performance
CHEN Bin,TONG Chuangming,LI Ximin,WANG Yizhe
(Air and Missile Defense College, Air Force Engineering University, Xi′an 710051, China)
To solve the problem of difficult detection for stealth target on monostatic radar, a method of stealth target detection is proposed based on the detection performance of netted radar. On the foundation of deducing radar equation, the detection coverage for stealth target on monostatic and bistatic radar is calculated and analyzed, combined with the Swerling1 target model and the domain decomposition method. Then the monostatic and bistatic RCS of structural stealth target is simulated and analyzed utilizing physical optics and method of equivalent currents. Moreover, the detection ability and configuration efficiency of network is resolved respectively by monostatic and bistatic radar combined with the typical configuration condition, such as equilateral triangle, square and honeycombed positon. Thus the optimal configuration and network mode are selected. Finally, Theoretical analysis and simulation results prove the applicability and feasibility of proposed configuration.
stealth target; detection performance; radar network; detection coverage
10.16592/ j.cnki.1004-7859.2016.03.004
国家自然科学基金资助项目(61372033);航空基金资助项目(20130196005)
陈彬 Email:chen_cem@126.com
2015-10-12
2015-12-16
TN911.7
A
1004-7859(2016)03-0018-05
